Metr kwadratowy dachówki kosztuje $25 \mathrm{zł}$. Obliczymy koszt pokrycia dachu w kształcie ostrosłupa o podstawie prostokąta (rysunek ostrosłupa poniżej). Przy obliczeniach przyjmiemy, że $10\%$ zakupionej dachówki nie zostanie wykorzystane.

R1BFgWVhJ3STS

Ilustracja przedstawia ostrosłup, którego podstawą jest prostokąt. Jeden z boków prostokąta ma długość 12 metrów. Krawędź boczna ostrosłupa ma długość 8 metrów, kąt pomiędzy dwoma krawędziami bocznymi, które przylegają do krawędzi podstawy o nieznanej długości ma wartość 86 stopni.

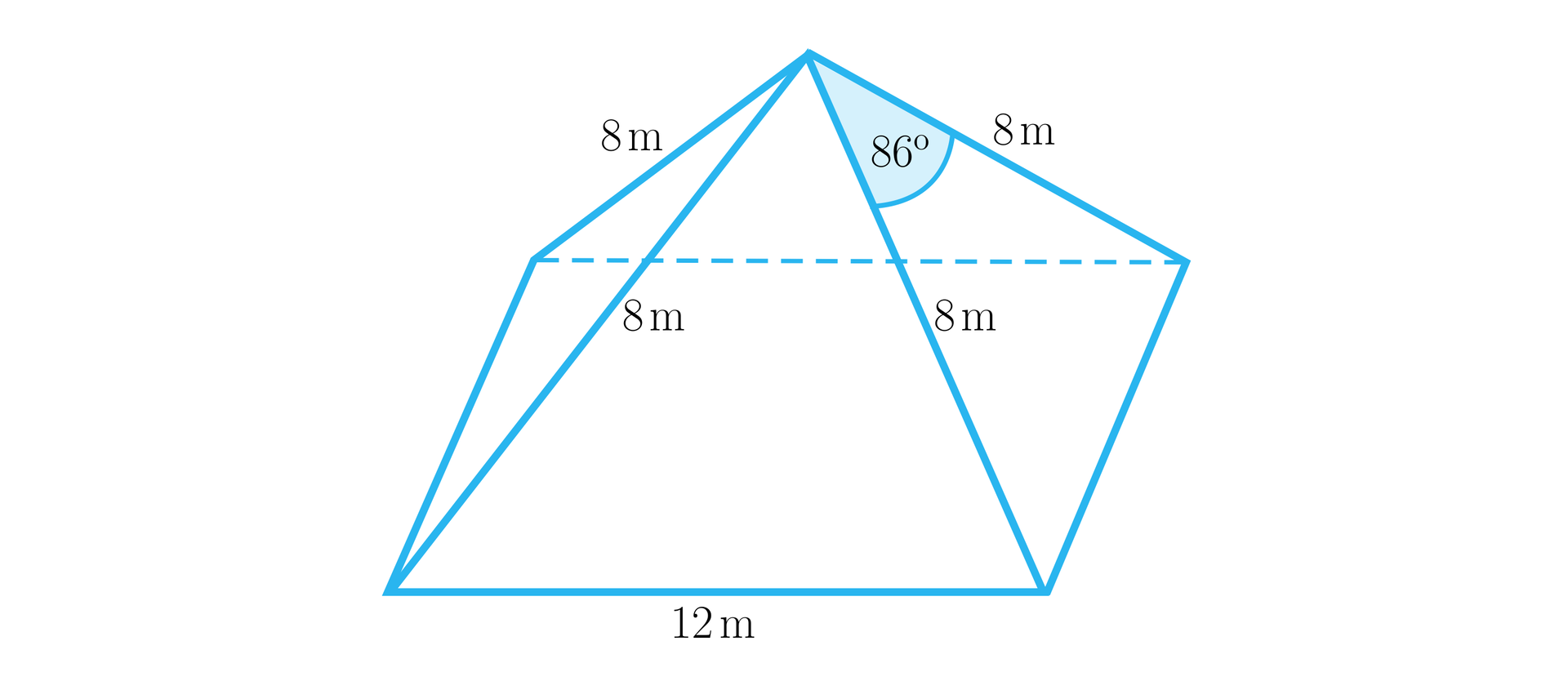
Rozwiązanie:

W zadaniu należy obliczyć pole powierzchni bocznej ostrosłupa.

Zaczniemy od policzenia długości drugiej krawędzi podstawy. Oznaczymy ją jako $x$. Zaznaczymy także wysokości ścian bocznych $h_1$ i $h_2$.

RK8YCBRI6zwRu

Ilustracja przedstawia ostrosłup, którego podstawą jest prostokąt. Jeden z boków prostokąta ma długość 12 metrów. Krawędź boczna ostrosłupa ma długość 8 metrów, kąt pomiędzy dwoma krawędziami bocznymi, które przylegają do krawędzi podstawy o nieznanej długości ma wartość 86 stopni. W ścianie bocznej, o podstawie o długości 12 metrów narysowano wysokość i podpisano ją $h_1$. W śćianie bocznej, w której kat między krawędziami wynosi 86 stopni zaznaczono wysokość i podpisano ją $h_2$, krawędź podstawy, do której przylega ta ściana podpisano literą x.

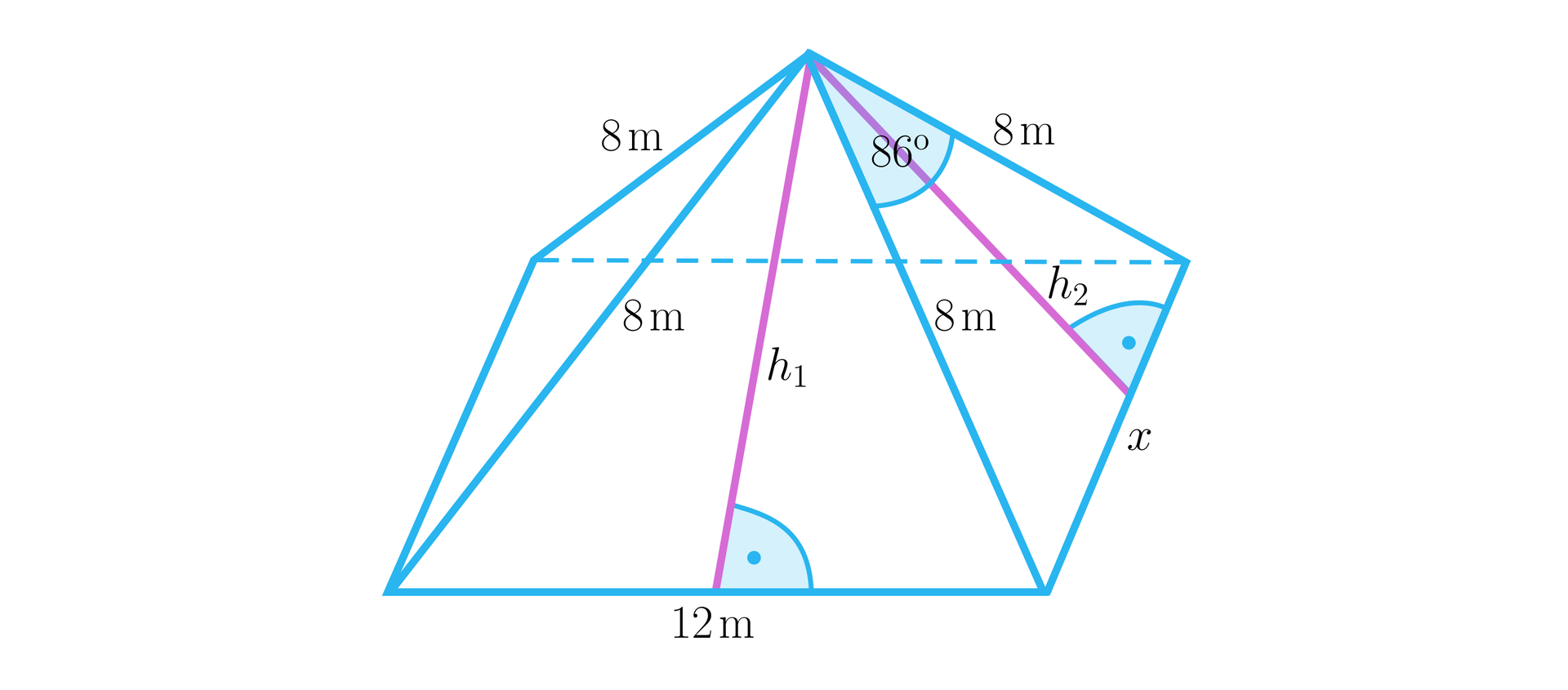
Z twierdzenia cosinusów mamy:

$x^2=8^2+8^2-2·8·8·\cos 86°$

$x^2\approx 119$

$x\approx 10,9 \mathrm{m}$

Ściany boczne są trójkątami równoramiennymi. Wyznaczymy długości ich wysokości. Nazwiemy je odpowiednio $h_1$ i $h_2$.

$h_1^2=8^2-6^2$

$h_1^2=28$

$h_1=2\sqrt{7}\approx 5,3 \mathrm{m}$

$P_1=31,8 {\mathrm{m}}^2$

$h_2^2=8^2-5,{45}^2$

$h_2^2\approx 34,3$

$h_2\approx 5,9 \mathrm{m}$

$P_2=32,2 {\mathrm{m}}^2$

$P_b=2·31,8+2·32,2=128 {\mathrm{m}}^2$

Dokładamy $10\%$ na tzw. odpad, więc potrzebujemy $1,1·128=140,8 {\mathrm{m}}^2$ blachodachówki.

$140,8 {\mathrm{m}}^2·25 \frac{\mathrm{zł}}{{\mathrm{m}}^2}=3520 \mathrm{zł}$.

Wigwam o wysokości $6 \mathrm{m}$, w kształcie ostrosłupa prawidłowego sześciokątnego, pokryto gontem bitumicznym.

RoIct5BztWSjV

Zdjęcie przedstawia wigwam, czyli namiot wykonany z drewnianych badyli i materiałowej narzuty. Obiekt ten ma kształt ostrosłupa i znajduje się na łące.

Obliczymy, ile go potrzeba, jeśli wiemy, że pokryto nim $5$ ścian, które są nachylone do podstawy pod kątem $60°$.

Rozwiązanie:

Wykonamy rysunek pomocniczy. Wprowadzimy dodatkowe oznaczenia. Niech $a$ – długość wysokości trójkąta równobocznego, na jakie został podzielony sześciokąt foremny, oraz $x$ – długość krawędzi podstawy.

R1B8SDk6qukQ3

Ilustracja przedstawia ostrosłup, którego podstawą jest sześciokąt foremny. Krawędź podstawy oznaczono literą x. Wierzchołek ostrosłupa oznaczono literą S, spodek wysokości poprowadzonej z tego wierzchołka oznaczono literą O. W ostrosłupie zaznaczono trójkąt prostokątny składający się z wysokości ostrosłupa, odcinka AS zaznaczonego w ścianie ostrosłupa, gdzie punkt A leży na krawędzi podstawy oraz odcinka OA leżącego w płaszczyźnie podstawy. Kąt AOS jest kątem prostym. Kąt OAS ma wartość 60 stopni. Wysokość ostrosłupa ma długość sześć.

Z zależności w trójkącie prostokątnym o kątach $30°$, $60°$, $90°$:

$6=a\sqrt{3}$

$a=2\sqrt{3}$

Zatem $\left|OA\right|=2\sqrt{3}$, $\left|SA\right|=4\sqrt{3}$.

Obliczymy długość krawędzi podstawy. Odcinek $OA$ jest wysokością trójkąta równobocznego, więc $2\sqrt{3}=\frac{x\sqrt{3}}{2}$, $x=4$.

Pole ściany bocznej ma miarę:

$P=\frac{1}{2}\cdot 4\cdot 4\sqrt{3}\approx 13,856 {\mathrm{m}}^2$.

Gontem pokryto $5$ ścian, więc potrzebujemy go

$13,856\cdot 5\approx 69,3 {\mathrm{m}}^2$.

R9x7hkVaqXstu

Grafika przedstawia budkę dla ptaków w kształcie ostrosłupa o podstawie trójkąta, w jednej ze ścian wycięty został okrągły otwór. Budka znajduje się na gałęzi.

Karmnik dla ptaków ma mieć kształt czworościanu foremnego o krawędzi długości $80 \mathrm{cm}$. Aby go precyzyjnie wykonać, trzeba znać miary kątów pomiędzy sąsiednimi ścianami bocznymi, kąt nachylenia krawędzi bocznej do płaszczyzny podstawy i kąt nachylenia ścian bocznych do płaszczyzny podstawy. Obliczymy je.

Rozwiązanie:

Ściany boczne są trójkątami równobocznymi o boku długości $80 \mathrm{cm}$. Odcinki zaznaczone na rysunku jako $x$ są wysokościami tych trójkątów.

Zaczniemy od kąta pomiędzy sąsiednimi ścianami bocznymi. Wykonamy rysunek pomocniczy. Wprowadzimy dodatkowe oznaczenie:

$x$ - wysokość ścian bocznych,

$\alpha$ - kąt pomiędzy dwoma sąsiednimi ścianami.

RAZlhKK3YuyyN

Ilustracja przedstawia ostrosłup o podstawie trójkąta A B C, długość krawędzi AB wynosi 80 centymetrów. Wierzchołek górny ostrosłupa podpisano literą S. W ścianie bocznej A B S zaznaczono wysokość, opuszczoną z wierzchołka A na krawędź BS, spodek tej wysokości podpisano literą D. W ścianie BCS również zaznaczono wysokość opuszczoną z wierzchołka C na krawędź BS, długość tej wysokości ma długość x, a spodek tej wysokości to punkt D. Kąt ADC podpisano literą alfa.

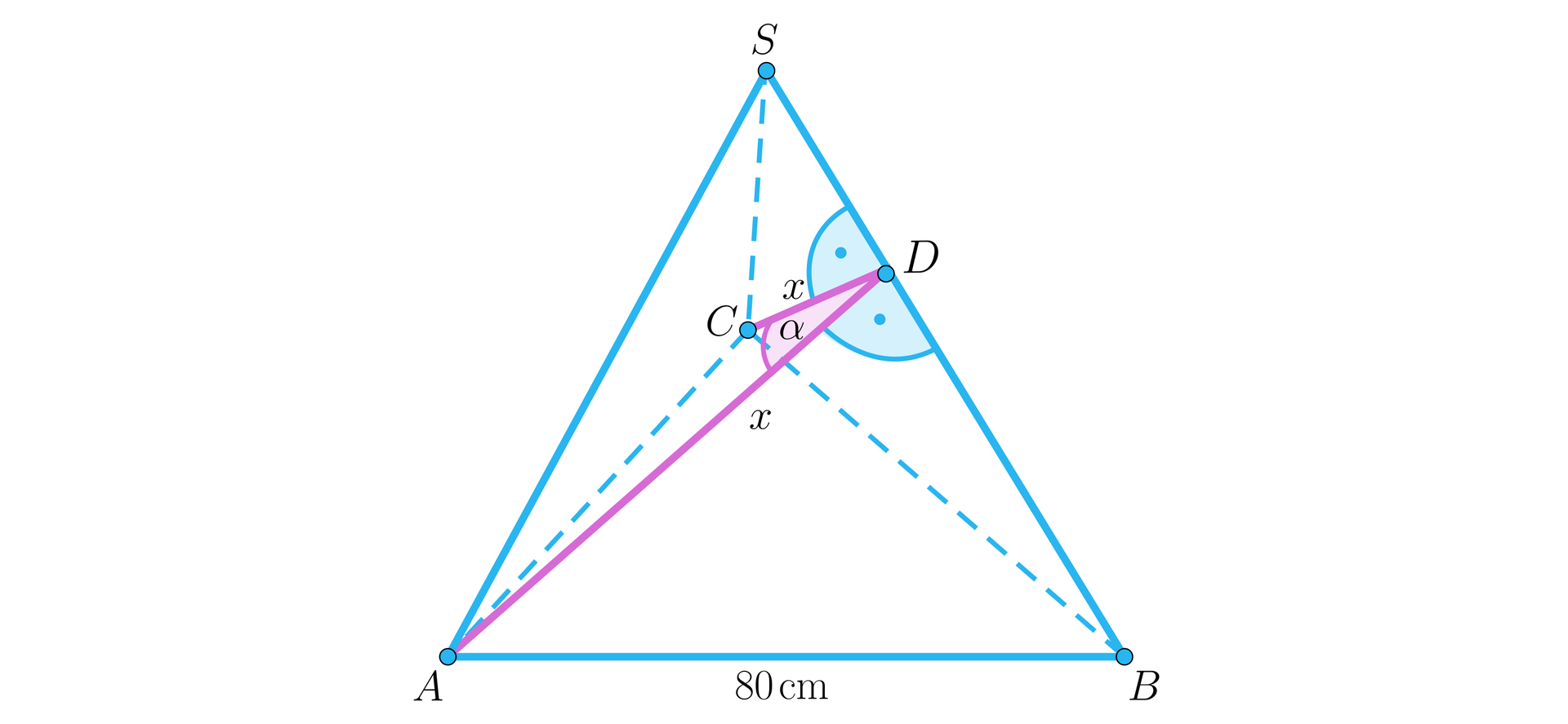
Ściany boczne są trójkątami równobocznymi o boku długości $80 \mathrm{cm}$. Odcinki zaznaczone na rysunku jako $x$ są wysokościami tych trójkątów.

$x=\frac{80\sqrt{3}}{2}=40\sqrt{3}$

Aby obliczyć miarę kąta $\alpha$, wykorzystamy twierdzenie cosinusów:

${80}^2=x^2+x^2-2x^2\cos \alpha$

$6400=4800+4800-9600\cos \alpha$

$\cos \alpha =\frac{1}{3}$

$\alpha \approx 70°$

Obliczymy teraz miarę kąta nachylenia ściany bocznej do płaszczyzny podstawy.

R14r11ftFgVhc

Ilustracja przedstawia ostrosłup o podstawie trójkąta A B C, długość krawędzi AB wynosi 80 centymetrów. Wierzchołek górny ostrosłupa podpisano literą S. Spodek wysokości opuszczonej z wierzchołka S podpisano literą O. W ostrosłupie zaznaczono trójkąt, składający się z wysokości ostrosłupa, odcinka ES, przy czym punkt E leży na krawędzi podstawy BC oraz odcinka OE leżącego w płaszczyźnie podstawy. Kąt OES podpisano literą alfa. Kąt EOS to kąt prosty. Odcinek OE podpisano literą r.

$\beta$ - kąt nachylenia ściany bocznej do płaszczyzny podstawy,

$r$ - promień okręgu wpisanego w trójkąt równoboczny.

$r=\frac{80\sqrt{3}}{6}=\frac{40\sqrt{3}}{3}$

$x$ - wysokość trójkąta równobocznego

$x=\frac{80\sqrt{3}}{2}=40\sqrt{3}$

$\cos \beta =\frac{r}{x}$

$\cos \beta =\frac{\frac{40\sqrt{3}}{3}}{40\sqrt{3}}=\frac{1}{3}$

$\beta \approx 70°$

Policzymy miarę kąta nachylenia krawędzi bocznej do płaszczyzny podstawy.

RYl8CwEk7wpXj

Ilustracja przedstawia ostrosłup o podstawie trójkąta A B C, długość krawędzi AB wynosi 80 centymetrów. Wierzchołek górny ostrosłupa podpisano literą S. Spodek wysokości opuszczonej z wierzchołka S podpisano literą O. W ostrosłupie zaznaczono kolorem dwa odcinki SO oraz OA. Kąt OAS podpisano literą gamma. Odcinek OA podpisano literą R.

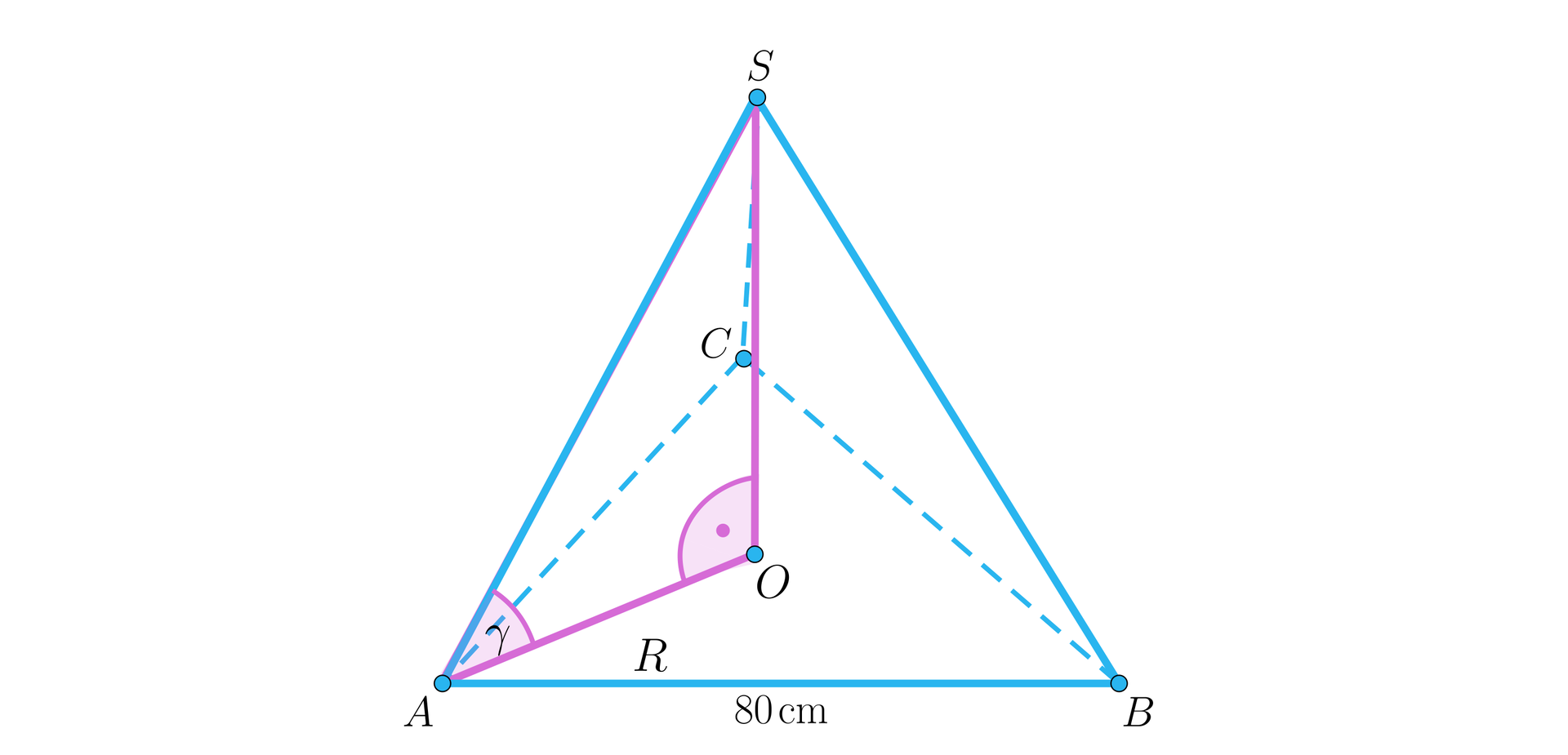
$\gamma$ - kąt nachylenia krawędzi bocznej do płaszczyzny podstawy,

$R$ - promień okręgu opisanego na trójkącie równobocznym.

$R=\frac{80\sqrt{3}}{3}$

$\mathrm{cos\gamma }=\frac{\frac{80\sqrt{3}}{3}}{80}=\frac{\sqrt{3}}{3}$

$\gamma \approx {55}^{\circ }$

Architekt zaprojektował dach domu w kształcie ostrosłupa prostegoostrosłup prostyostrosłupa prostego o podstawie prostokąta o wymiarach $8 \mathrm{m}\times 6 \mathrm{m}$. Z projektu wynika, że tangens kąta nachylenia krawędzi bocznej do płaszczyzny podstawy ostrosłupa wynosi $\frac{1}{5}$. Aby dobrze wymierzyć rozmieszczenie kalenic, musimy poznać miarę kątów płaskich przy wierzchołku ostrosłupa. Wyznaczymy ich miarę.

Rozwiązanie:

Wykonamy rysunek pomocniczy. Wprowadzimy oznaczenie pomocnicze: niech $d$ – długość przekątnej prostokąta, $H$ – długość wysokości ostrosłupa, $x$ – długości krawędzi bocznych, $\gamma$ - miara kąt nachylenia krawędzi bocznej do płaszczyzny podstawy.

RI96pGl6iWsrj

Ilustracja przedstawia ostrosłup, którego podstawą jest prostokąt o długości boków 8 oraz sześć. W podstawie zaznaczono jej przekątną i podpisano ją literą d. Kąt pomiędzy krawędzią boczną, a przekątną podstawy podpisano literą gamma. Długość krawędzi bocznej podpisano literą x. Spodek wysokości H leży na przekątnej podstawy.

$d^2=8^2+6^2$

$d=10$

$\mathrm{tg}\gamma =\frac{H}{\frac{1}{2}d}$

$\frac{1}{5}=\frac{H}{5}$

$H=1$

$x$ - długości krawędzi bocznych

$x^2=1^2+5^2$

$x=\sqrt{26}$

Zobaczmy na rysunku, gdzie leżą kąty płaskie przy wierzchołku ostrosłupakąt płaski przy wierzchołku ostrosłupakąty płaskie przy wierzchołku ostrosłupa. Oznaczmy je jako $\alpha$ i $\beta$.

R1E69qLdgKTXc

Ilustracja przedstawia ostrosłup, którego podstawą jest prostokąt o długości boków 8 oraz sześć. Kąt pomiędzy krawędziami bocznymi, ściany bocznej przylegającej do krawędzi podstawy o długości 6 podpisano literą alfa. Kąt pomiędzy krawędziami bocznymi, ściany bocznej przylegającej do krawędzi podstawy o długości 8 podpisano literą beta. Długość krawędzi bocznych podpisano literą x.

Z twierdzenia cosinusów mamy:

$6^2=x^2+x^2-2x^2\cos \alpha$

$36=26+26-52\cos \alpha$

$\cos \alpha =\frac{16}{52}=\frac{4}{13}$

$\alpha \approx 72°$

$8^2=x^2+x^2-2x^2\cos \beta$

$64=26+26-52\cos \beta$

$\cos \beta =-\frac{12}{52}=-\frac{3}{13}$

$\beta \approx 103°$

Zatem kąty płaskie mają odpowiednio miary $72°$ i $103°$.

Pan Marek wybudował drewnianą altanę w kształcie ostrosłupa prawidłowegoostrosłup prawidłowyostrosłupa prawidłowego czworokątnego o krawędzi podłogi $4 \mathrm{m}$. Kąt nachylenia krawędzi bocznych do płaszczyzny podstawy wynosi $45°$. Postanowił zabudować $3$ ściany boczne  deskami o grubości $2,5 \mathrm{cm}$. Metr sześcienny deski kosztuje $700 \mathrm{zł}$. Obliczymy koszt desek potrzebnych na obicie altanki oraz jej kubaturę.

R1F7oK1h6EK0c

Grafika przedstawia altanę wykonaną z drewna, w kształcie ostrosłupa o podstawie kwadratu. Jedna ze ścian bocznych oraz podstawa zostały usunięte. Zatem z drewna wykonane zostały 3 ściany boczne.

Rozwiązanie:

Wykonamy rysunek pomocniczy. Niech $H$ oznacza długość wysokości ostrosłupa.

W podstawie mamy kwadrat o krawędzi długości $4 \mathrm{m}$, więc jego przekątna ma długość $4\sqrt{2} \mathrm{m}$.

R1YrGLD4k71vT

Ilustracja przedstawia ostrosłup o podstawie czworokąta A B C D, krawędź AB ma długość 4 metry, krawędź BC ma również długość 4 metry. W podstawie zaznaczono przekątną AC, która ma długość $4\sqrt{2}$. Kąt pomiędzy przekątną AC i krawędzią boczną CS ma wartość 45 stopni. W ostrosłupie z wierzchołka górnego S opuszczono wysokość, której spodek O leży na przekątnej AC.

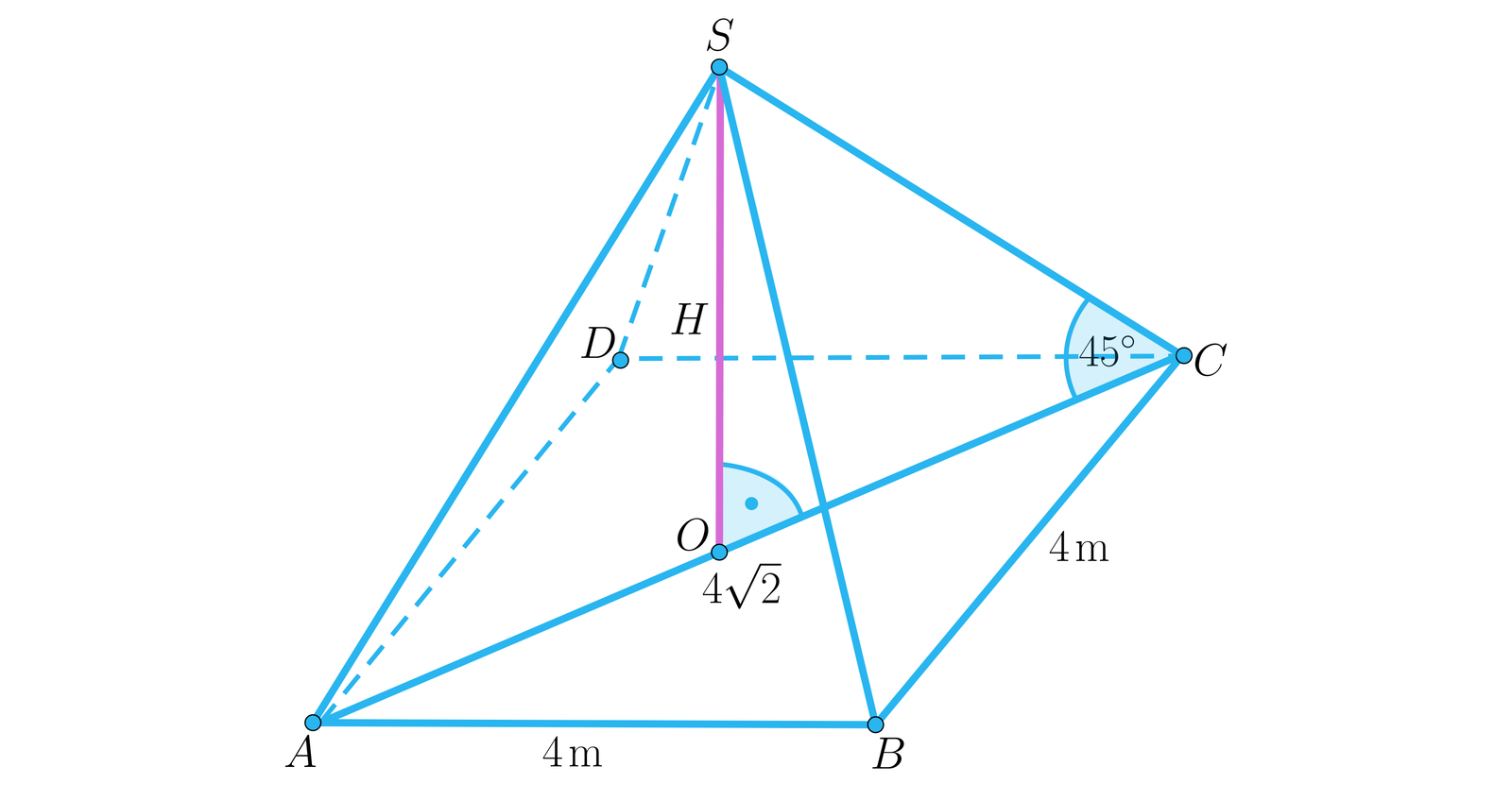
Trójkąt $SOC$ jest prostokątny równoramienny. $\left|OC\right|=2\sqrt{2}$. Zatem również $H=2\sqrt{2}$, stąd krawędzie boczne ostrosłupa mają długość $4 \mathrm{m}$ a ściany boczne są trójkątami równobocznymi.

Obliczymy pole jednej zabudowanej ściany bocznej:

$P_{bś}=\frac{4^2\sqrt{3}}{4}=4\sqrt{3}\approx 6,93 {\mathrm{m}}^2$

Jeśli pole ściany bocznej pomnożymy przez grubość deski, to otrzymamy ilość metrów sześciennych desek potrzebnych na jej obudowanie:

$2,5 \mathrm{cm} = 0,025 \mathrm{m}$

$6,93 {\mathrm{m}}^2·0,025 \mathrm{m}\approx 0,17 {\mathrm{m}}^3$

Mamy trzy ściany, więc potrzebujemy: $0,17 {\mathrm{m}}^3· 3 = 0,51 {\mathrm{m}}^3$ desek.

Policzymy koszt desek:

$700 · 0,51 \approx 357 \left[\mathrm{zł}\right]$.

Obliczymy na koniec kubaturę altany (objętość ostrosłupa): $V=\frac{1}{3}{P}_p H=\frac{1}{3} · 4^2 · 2\sqrt{2}=\frac{32\sqrt{2}}{3}\approx 15,08 \left[{\mathrm{m}}^3\right]$

Odpowiedź: Koszt obudowy $3$ ścian altanki potrzeba $357 \mathrm{zł}$. Kubatura altanki wynosi $15,08 {\mathrm{m}}^3$.

ostrosłup prosty, w którym podstawa jest wielokątem foremnym

ostrosłup, w którym spodek wysokości pokrywa się ze środkiem okręgu opisanego na podstawie. Krawędzie boczne ostrosłupa prostego są tej samej długości

kąt pomiędzy ramionami trójkąta równoramiennego będącego jego ścianą boczną