Przeczytaj
Przypomnij sobie najpierw definicję algebraiczną wartości bezwzględniej liczby rzeczywistej .
Oblicz wartość wyrażenia
.
Obliczamy najpierw wartości modułów, które pojawiły się w przykładzie.
Korzystamy z definicji wartości bezwzględnej liczby rzeczywistej.
Następnie, pamiętając o kolejności wykonywania działań, obliczamy wartość wyrażenia .
Oblicz wartość wyrażenia
.
Obliczamy najpierw wartości modułów, które pojawiły się w przykładzie.
Ponownie korzystamy z definicji wartości bezwzględnej liczby rzeczywistej.
Ostatnią wartość bezwzględną możemy obliczyć dwoma sposobami.
I sposób
Doprowadzamy wyrażenie pod modułem do najprostszej postaci i określamy jego znak, a następnie opuszczamy symbol wartości bezwzględnej.
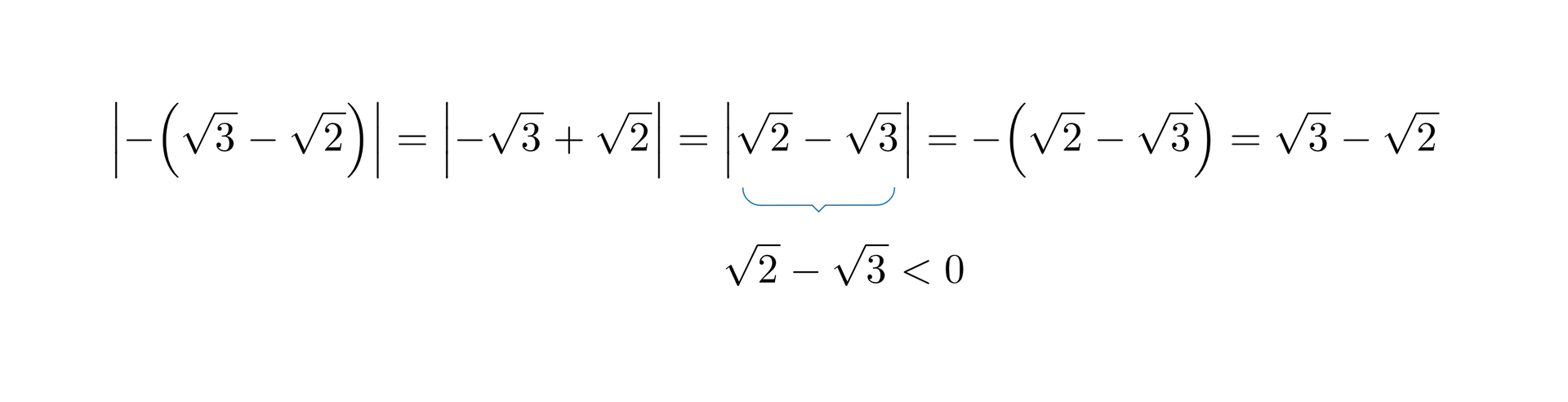
II sposób
Określamy znak wyrażenia pod modułem i opuszczamy symbol wartości bezwzględnej.

Teraz, pamiętając o kolejności wykonywania działań oraz zasadach dodawania i odejmowania pierwiastków, obliczamy wartość wyrażenia .
Pierwiastki, które maja taka samą liczbę podpierwiastkową oznaczono takim samym kolorem.
Przypomnij sobie poznane własności wartości bezwzględnej liczby rzeczywistej.
,
,
,
, ,
, ,
Zapisz wyrażenie w najprostszej postaci, wiedząc, że .
Określamy znak wyrażeń znajdujących się pod symbolami wartości bezwzględnej aby, korzystając z definicji, opuścić te symbole.
Możemy to zrobić następująco:
Korzystamy z założenia:
.Odejmujemy od obu stron nierówności , tak aby po lewej stronie nierówności otrzymać wyrażenie tożsame z tym, które znajduje się w pierwszej wartości bezwzględnej.
Otrzymaliśmy nierówność, dzięki której wiemy, że wyrażenie znajdujące się pod pierwszym modułem jest ujemne, a zatem:
.Ponownie korzystamy z założenia
.Tym razem od obu stron nierówności odejmujemy , tak aby po lewej stronie nierówności otrzymać wyrażenie tożsame z tym, które znajduje się w drugiej wartości bezwzględnej.
A zatem wyrażenie znajdujące się pod drugim modułem jest również ujemne, stąd:
.
Zapisujemy wyrażenie w najprostszej postaci, dla .
Zapisz wyrażenie w najprostszej postaci, wiedząc, że .
Określamy znak wyrażeń znajdujących się pod symbolami wartości bezwzględnej aby, korzystając z definicji, opuścić te symbole.
Możemy to zrobić następująco:
Korzystamy z założenia
.Otrzymaliśmy nierówność, dzięki której wiemy, że wyrażenie znajdujące się w pierwszym module jest nieujemne, a zatem
.Ponownie korzystamy z założenia.
Tym razem, aby otrzymać wyrażenie, które znajduje się w drugiej wartości bezwzględnej, musimy dokonać przekształceń.
– mnożymy strony nierówności przez
– do stron nierówności dodajemy :
.A zatem wyrażenie znajdujące się w drugim module jest również nieujemne, stąd:
.
Zapisujemy wyrażenie w najprostszej postaci, dla .
Zapisz wyrażenie bez użycia symbolu wartości bezwzględnej, dla .
W tym przykładzie najpierw zapisujemy wyrażenie bez symbolu wartości bezwzględnej zgodnie z definicją modułumodułu.
czyli
Zapisujemy wyrażenie bez użycia symbolu wartości bezwzględnej.
dla
dla
Podsumowując:
Zapisz wyrażenie bez użycia symbolu wartości bezwzględnej, dla .
Najpierw zapisujemy wyrażenia bez symbolu wartości bezwzględnej zgodnie z definicją modułu.
czyli
oraz
czyli
Możemy wykonać rysunek pomocniczy, na którym zaznaczymy znak wartości wyrażeń znajdujących się w modułach, w wyznaczonych wyżej przedziałach liczbowych.

A zatem:
1. Dla mamy:
, więc i , więc .
2. Dla mamy:
, więc i , więc .
3. Dla mamy:
, więc i , więc .
Zapisujemy wyrażenie bez użycia symbolu wartości bezwzględnej.
1. Dla :
.
2. Dla :
.
3. Dla :
.
Podsumowując:
.
Słownik
wartość bezwzględna liczby rzeczywistej