Sieci przepływowe

Siecią przepływowąsieć przepływowaSiecią przepływową nazywamy taki graf spójnygraf spójnygraf spójny skierowany, którego każda krawędź przypisaną ma daną przepustowośćprzepustowośćprzepustowość, dzięki czemu między krawędziami może odbywać się – zgodny z kierunkiem krawędzi – przepływ.

Przeanalizujmy graf spójny skierowany.

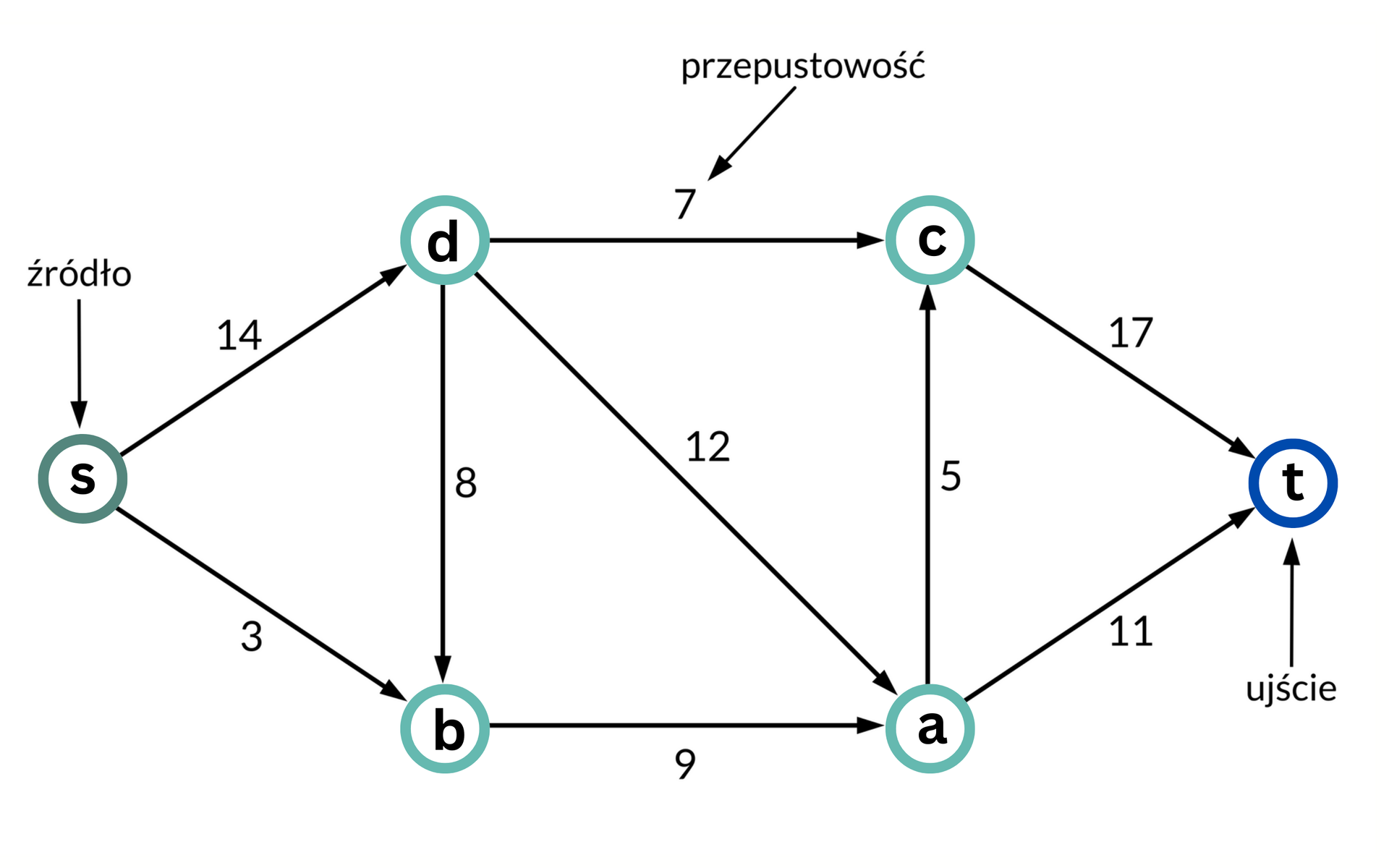
Dany jest grafgrafgraf spójny skierowany $G=(E,V)$, który składa się ze zbioru wierzchołków $V$ oraz ze zbioru krawędzi skierowanych $E$.

Każdej krawędzi przypisana jest pewna wartość – to przepustowość krawędzi. Przepustowość to maksymalna ilość pewnego czynnika, który przepływa przez sieć. Wartość przepustowości możemy opisać następująco: $c(v,w)\;\in\;E$

Dodatkowo oznaczmy dwa wierzchołki grafu: wierzchołek $s$ (oznaczony na ilustracji S) będzie źródłemźródłoźródłem, a wierzchołek $t$ (oznaczony na ilustracji T) – ujściemujścieujściem.

Źródłem nazywamy wierzchołek, z którego wychodzą przepływy, natomiast ujściem nazywamy wierzchołek, do którego prowadzą przepływy.

RTw43lwoq8a8m

Ilustracja przedstawia graf będący siecią przepływową. Graf składa się z sześciu punktów i dziewięciu strzałek. Układ punktów jest następujący. Punkty a, b c oraz d leżą na wierzchołkach kwadratu, punk s leży po lewej stronie kwadratu, a strzałki wychodzące od niego do wierzchołków kwadratu tworzą trójkąt równoramienny, analogicznie punkt t znajduje się po prawej stronie kwadratu. Punkt s jest podpisany jako źródło. Punkt t jako ujście, a liczby znajdujące się przy strzałkach to przepustowość. Przykładowo: Od punktu s do punktu b prowadzi strzałka z liczbą 3, od s do d z liczbą 14, od d do b z liczbą 8 od d do a z liczbą 14, od b do a z liczbą 9, od d do c z 7, od c do t z 17 od a do c z 5 od a do t z 11.

Przykładami sieci przepływowych są np. przepływ gazu, wody czy też  ruch drogowy. Przepływ danej krawędzi skierowanej to pewna wartość, jaką przypisujemy każdej krawędzi sieci. Wartość ta może być ujemna, jak i dodatnia.

Formalnie powiemy, że funkcję rzeczywistą $F:V\times V\to \mathrm{ℝ}$ pary wierzchołków sieci $G=(V,E)$ nazywamy przepływem, jeśli spełnia ona trzy wymienione niżej warunki.

Przepływ sieci $G(V,E)$ to suma wszystkich przepływów nettoprzepływ nettoprzepływów netto ze źródła $s$ do wszystkich innych wierzchołków sieci.

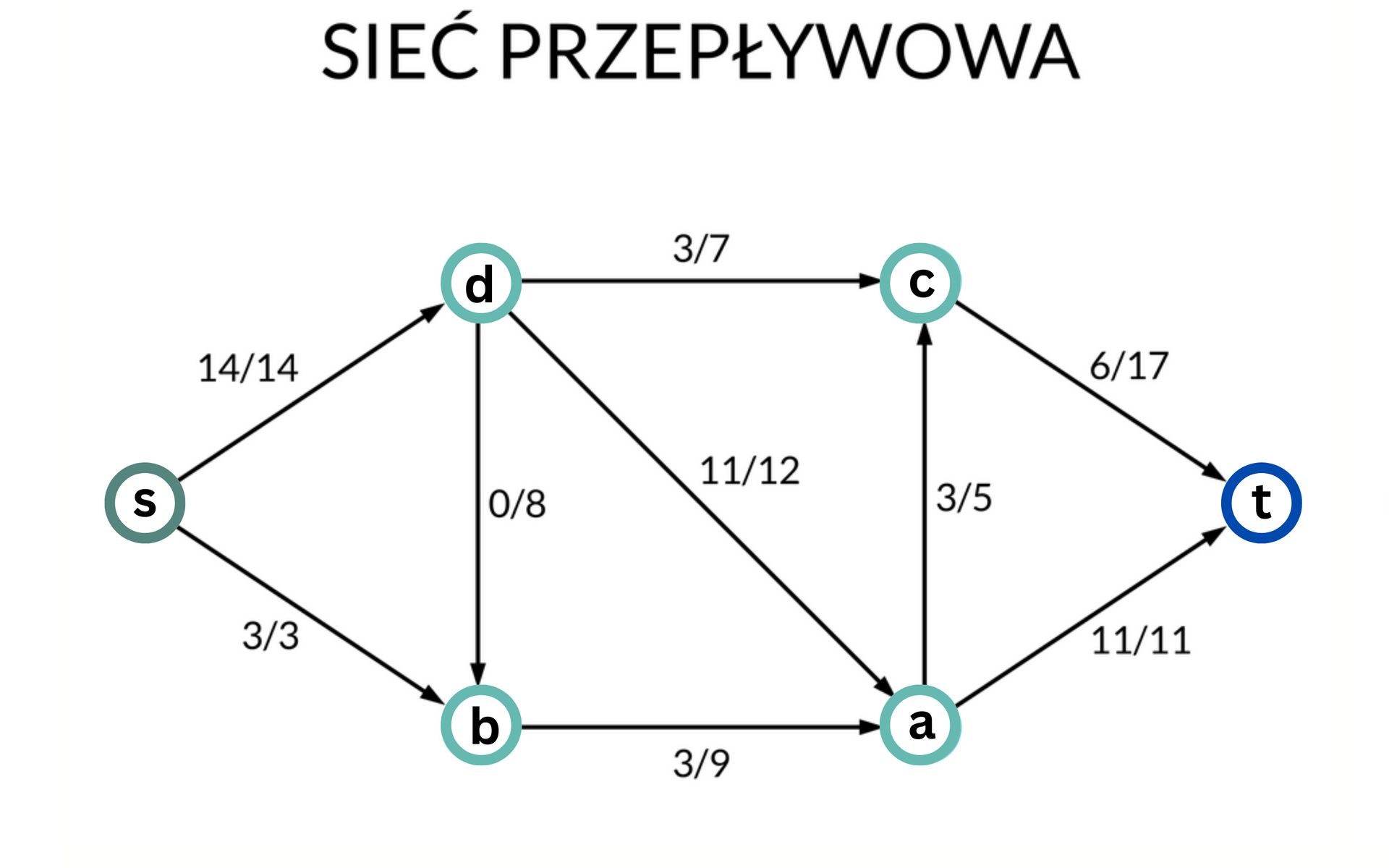
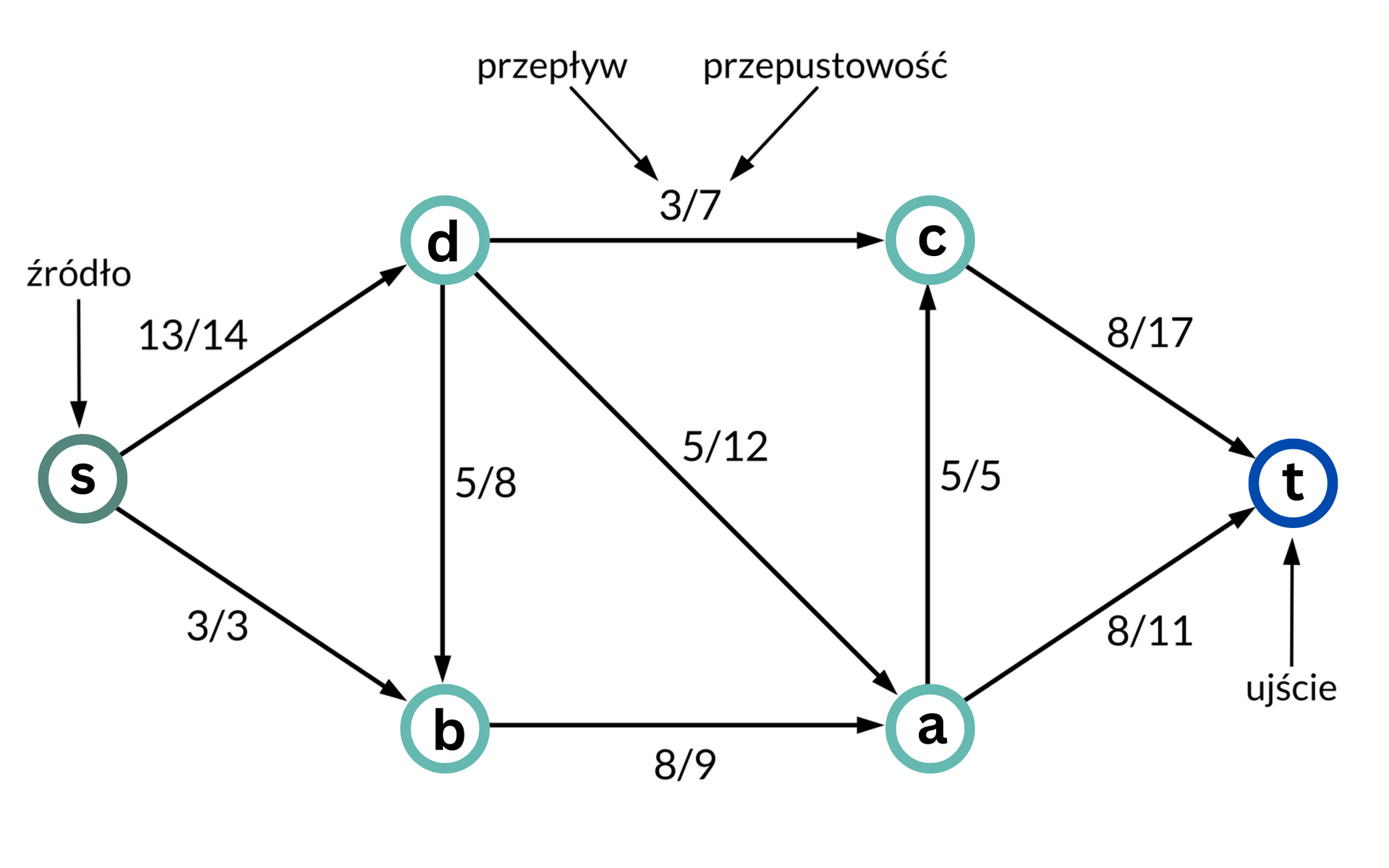
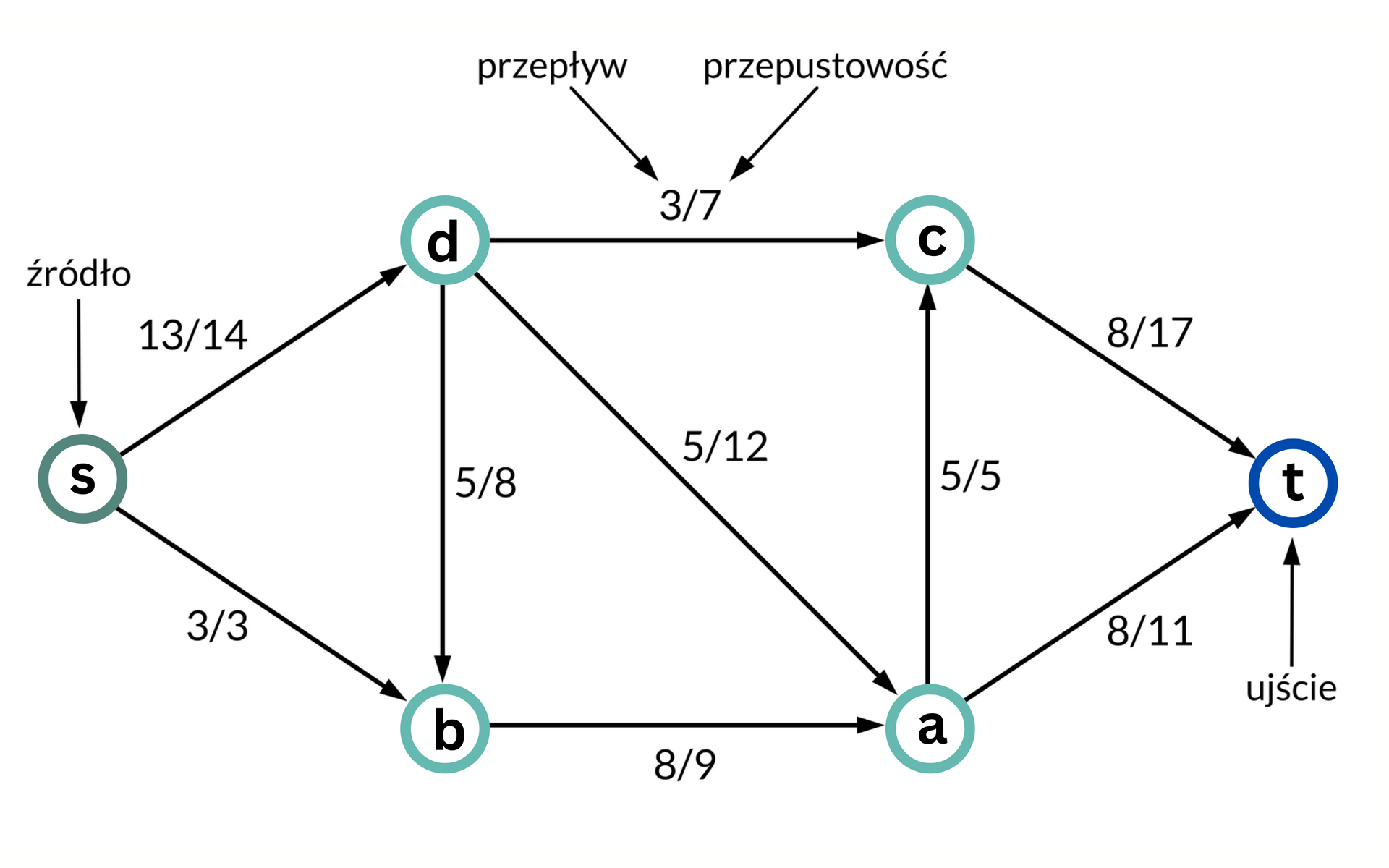
By lepiej zrozumieć to zagadnienie, przyjrzyjmy się uzupełnionej ilustracji umieszczonej w dalszej części e‑materiału.

Przypuśćmy, że w pewnej sieci $G=(V,E)$ każda krawędź $(v,w) \in E$ ma przepustowość $c(v,w)$ oraz przypisano jej przepływ $f(v,w)$. Na ilustracjach sieci przepływowej przepustowość i przepływ krawędzi oznaczmy, pisząc obok dwie liczby oddzielone ukośnikiem. Liczba na lewo od ukośnika oznacza przepływ krawędzi, a na prawo – przepustowość krawędzi.

Suma przepływów wychodzących ze źródła wynosi 16 (13 do wierzchołka D oraz 3 do wierzchołka B).

RqoNjCibNOo3v

Ilustracja przedstawia graf będący siecią przepływową. Graf składa się z sześciu punktów i dziewięciu strzałek. Układ punktów jest następujący. Punkty a, b c oraz d leżą na wierzchołkach kwadratu, punk s leży po lewej stronie kwadratu, a strzałki wychodzące od niego do wierzchołków kwadratu tworzą trójkąt równoramienny, analogicznie punkt t znajduje się po prawej stronie kwadratu. Punkt s jest podpisany jako źródło. Punkt t jako ujście. Przy każdej ze strzałek znajdują się dwie liczby oddzielone ukośnikiem. Są to przepływ oraz przepustowość. Z  punktu s do punktu d biegnie strzałka z liczbami trzynaście ukośnik czternaście, od S do B z trzy ukośnik trzy, z d do b z pięć ukośnik osiem, z b do a z osiem ukośnik dziewięć, z d do a z pięć ukośnik dwanaście, z d do c z trzy ukośnik siedem. Z a do c z pięć ukośnik pięć. Z a do t z osiem ukośnik jedenaście, z c do t z osiem ukośnik siedemnaście.

Z warunku skośnej symetriiwarunek skośnej symetriiwarunku skośnej symetrii możemy wywnioskować, że przypływ wychodzący ze źródła $s$ jest równy przepływowi docierającemu do ujścia $t$.

Możemy to sprawdzić – rzeczywiście suma przepływów wchodzących do ujścia wynosi 16 (8 z wierzchołka C oraz 8 z wierzchołka A).

Głównym problemem spotykanym przy zagadnieniu sieci przepływowej jest problem maksymalnego przepływu. Zadanie polega na wyznaczeniu maksymalnego przepływu sieci ze źródła do ujścia, biorąc pod uwagę ograniczenia związane z przepustowością każdej krawędzi. Dla ułatwienia możemy sobie wyobrazić krawędzie jako rury tworzące sieć połączeń wodociągowych ze źródła do ujścia. Problem maksymalnego przepływu polegałby tu na obliczeniu, ile wody można maksymalnie przepuścić ze źródła do ujścia. To, ile wody może przepłynąć przez każdą rurę, ogranicza jej przepustowość.

Algorytm Forda‑Fulkersona pomaga rozwiązać problem maksymalnego przepływu. Polega on na wyznaczeniu sieci rezydualnych oraz ścieżek rozszerzających.

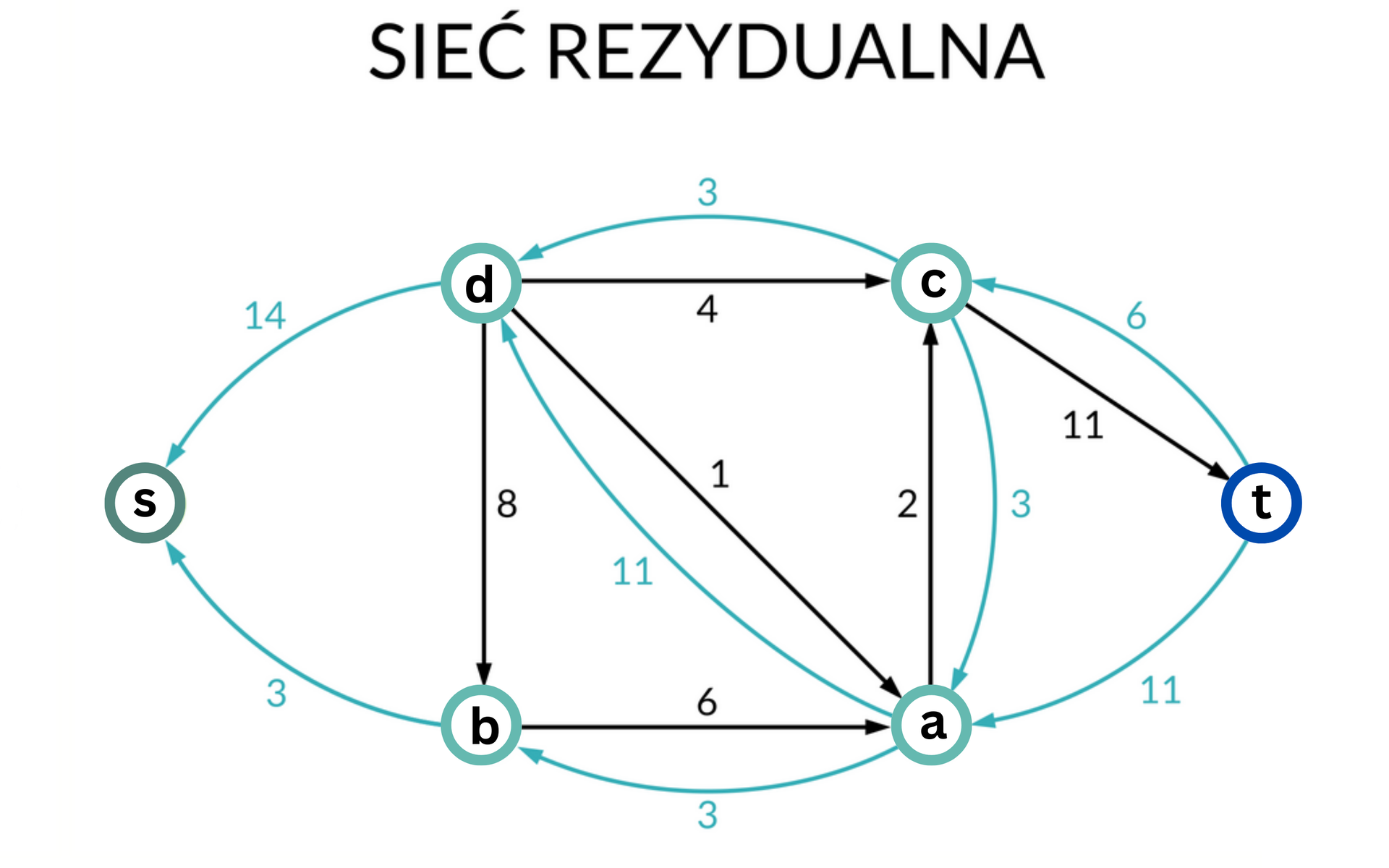
Siecią rezydualnąsieć rezydualnaSiecią rezydualną nazywamy graf, który jest tworzony na podstawie pierwotnej sieci przepływowej i aktualnego przepływu. Krawędzie w sieci rezydualnej reprezentują przepustowość rezydualną, czyli maksymalną ilość dodatkowych danych, które mogą przepłynąć daną krawędzią w danej chwili.

Ścieżkami rozszerzającymi nazywamy ścieżki w sieci rezydualnej, które umożliwiają dodanie dodatkowego przepływu do istniejącego przepływu w sieci przepływowej.

Wróćmy do zaprezentowanej wcześniej ilustracji:

RM2Li1Pwgnc2Q

Ilustracja przedstawia graf będący siecią przepływową. Graf składa się z sześciu punktów i dziewięciu strzałek. Układ punktów jest następujący. Punkty a, b c oraz d leżą na wierzchołkach kwadratu, punk s leży po lewej stronie kwadratu, a strzałki wychodzące od niego do wierzchołków kwadratu tworzą trójkąt równoramienny, analogicznie punkt t znajduje się po prawej stronie kwadratu. Punkt s jest podpisany jako źródło. Punkt t jako ujście. Przy każdej ze strzałek znajdują się dwie liczby oddzielone ukośnikiem. Są to przepływ oraz przepustowość. Z  punktu s do punktu d biegnie strzałka z liczbami trzynaście ukośnik czternaście, od S do B z trzy ukośnik trzy, z d do b z pięć ukośnik osiem, z b do a z osiem ukośnik dziewięć, z d do a z pięć ukośnik dwanaście, z d do c z trzy ukośnik siedem. Z a do c z pięć ukośnik pięć. Z a do t z osiem ukośnik jedenaście, z c do t z osiem ukośnik siedemnaście.

Przepustowość rezydualną $c_f(v,w)$ krawędzi $(v,w)$ definiujemy jako różnicę przepustowości $c(v,w)$ oraz przepływu $f(v,w)$ krawędzi.

Podstawmy konkretne wartości:

Zatem dla krawędzi $BA$, której przepływ to 8, a przepustowość to 9, przepustowość rezydualna wynosi 9 - 8, czyli 1. Jest to zapasowy przepust krawędzi.

Może występować przepływ w przeciwnym do krawędzi kierunku (ujemny).

Kierunek, w którym obliczamy przepustowość rezydualną, jest dowolny. Można obliczyć przepustowość rezydualną $c(w,v)$, choć nie istnieje w sieci krawędź zwrotna $(w,v)$. Jeśli nie istnieje krawędź $(w,v)$, to przepustowość $c(w,v)$ jest równa $0$. Oznacza to, że przepustowość rezydualna $c_f(w,v)$ jest równa aktualnemu przepływowi krawędzi $(v,w)$.

Również podstawmy konkretne wartości:

Dla kierunku przeciwnego przepust rezydualny jest równy samej wartości przepływu, czyli 8.

Przepustowość rezydualna wyznaczona w kierunku zgodnym z krawędzią jest zapasowym przepustem krawędzi, przez którą można jeszcze prowadzić przepływ. Natomiast przepustowość rezydualna wyznaczona w kierunku przeciwnym jest aktualną wartością przepływu krawędzi.

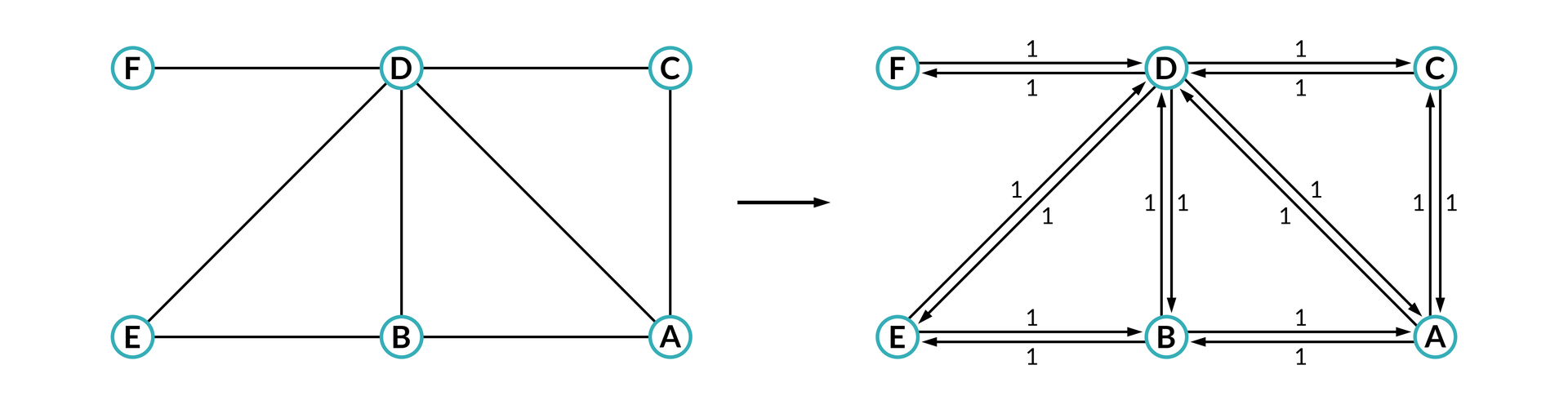
Na podstawie obliczonych przepustowości rezydualnych wyznaczamy sieć rezydualną. Jest to taka sieć, która przejmuje wierzchołki pierwotnej sieci przepływowej oraz tylko te krawędzie, których przepustowość rezydualna jest różna od zera. W sieci przepływowej każdej krawędzi pierwotnej odpowiadają dwie krawędzie skierowane w przeciwne strony.

Krawędzie sieci rezydualnej o kierunku zgodnym z pierwotną krawędzią oznaczają przepustowość rezydualną, czyli zapas przepływu. Krawędzie o zerowej przepustowości rezydualnej są zbędne w sieci rezydualnej, ponieważ nie pomieszczą więcej przepływu. Z tego powodu, jeśli przepustowość rezydualna jest równa 0, to takiej krawędzi nie rysujemy.

Krawędź w sieci rezydualnej przeciwna do kierunku pierwotnej krawędzi oznacza przepływ. Jeśli przepływ pewnej krawędzi jest zerowy, to krawędź także jest ignorowana.

Przyjrzyjmy się ilustracjom. Krawędź $BA$ to zapas przepływu danej sieci, natomiast krawędź $AB$ – aktualny przepływ.

Przy tworzeniu sieci rezydualnej będziemy szukać ścieżek ze źródła $s$ do ujścia $t$ we wszystkich możliwych parach wierzchołków. Każdą taką ścieżkę w grafie rezydualnym z wierzchołka $s$ do wierzchołka $t$ nazywamy ścieżką rozszerzającąścieżki rozszerzająceścieżką rozszerzającą, o ile nie zawiera cykli i jeśli każda krawędź ma dodatnią przepustowość rezydualną.

Problem niezawodności sieci

Przypuśćmy, że projektujemy sieć. Będzie się składała z routerów połączonych ze sobą kanałami komunikacyjnymi. Znając teorię grafów, możemy skorzystać z reprezentacji grafowej, która pozwoli nam dokładniej przeanalizować sprawność sieci. Routery przedstawimy jako wierzchołki, natomiast kanały będą reprezentowane przez krawędzie łączące routery.

R1ZNnaPGXMYH8

Ilustracja przedstawia sześć niebieskich krążków, na których znajdują się cztery strzałki. Krążki są połączone ze sobą czarnymi liniami. Krążki ułożone są w dwóch rzędach po trzy krążki.

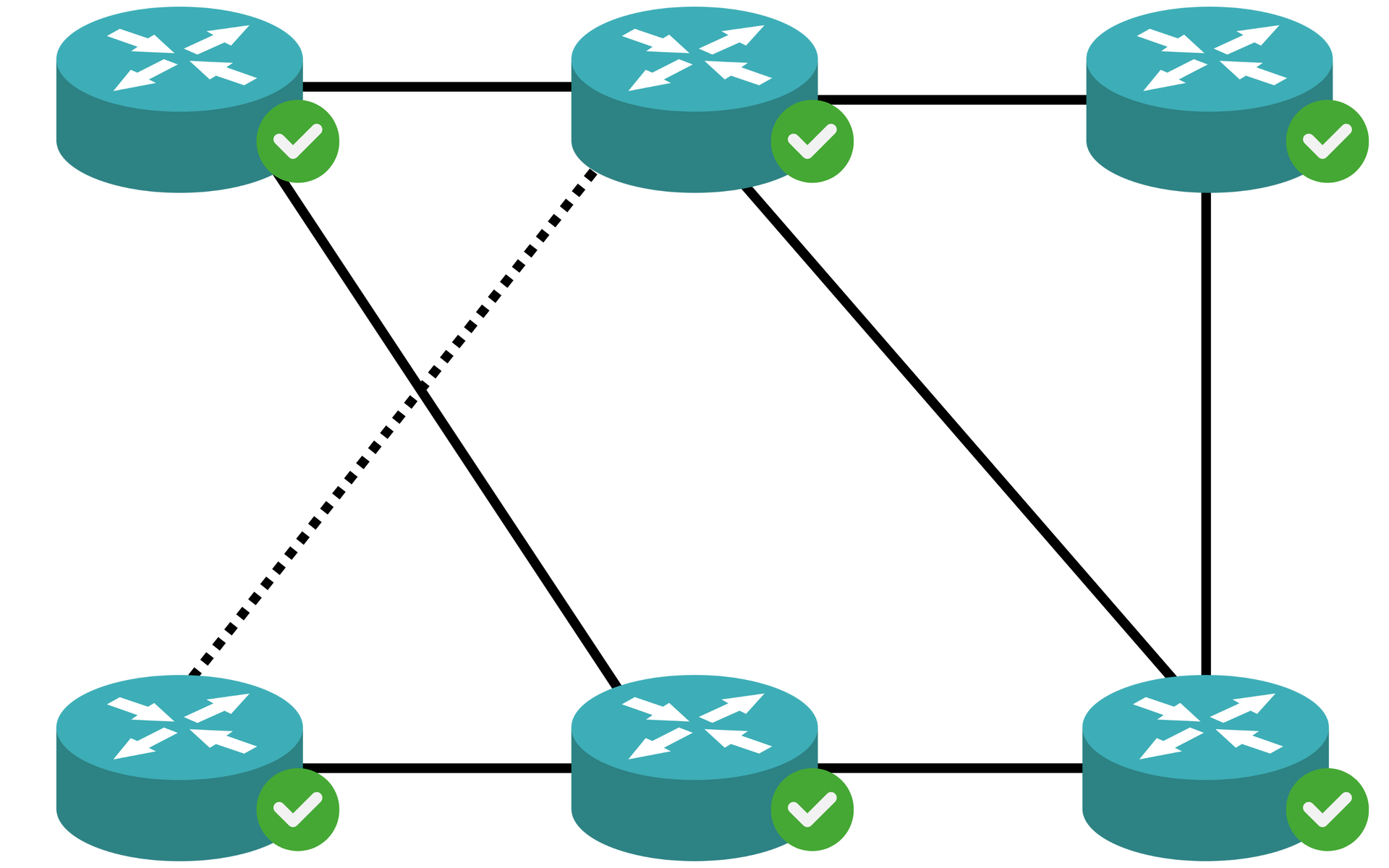
Chcemy uniknąć awarii całej sieci w sytuacji, gdyby niektóre połączenia zostały przerwane. W tym celu należy zapewnić bezpośrednie lub pośrednie połączenie między dwoma routerami. Dla grafu reprezentującego sieć routerów zdefiniujmy pojęcie spójności krawędziowej grafu.

Powiemy, że graf jest $k$-spójny krawędziowok‑spójność krawędziowa$k$-spójny krawędziowo, jeśli pozostanie spójny nawet wtedy, gdy zostanie usuniętych mniej niż $k$ dowolnych krawędzi. Wtedy spójność krawędziowa tego grafu jest największą liczbą krawędzi, po usunięciu których graf na pewno pozostanie spójny. W grafie może istnieć zbiór większej niż $k$ liczby krawędzi.

Usterka jednego kanału

RKNgVCgiaRIXN

Ilustracja przedstawia sześć niebieskich krążków, na których znajdują się cztery strzałki. Krążki są połączone ze sobą czarnymi liniami. Krążki ułożone są w dwóch rzędach po trzy krążki. Przy każdym z krążków znajduje się parafka oznaczająca znak wyboru. Pomiędzy drugim krążkiem z pierwszego rzędu a pierwszym krążkiem z drugiego rzędu znajduje się linia przerywana.

Awaria sieci

R3lUgb267DLL6

Ilustracja przedstawia sześć niebieskich krążków, na których znajdują się cztery strzałki. Krążki są połączone ze sobą czarnymi liniami. Krążki ułożone są w dwóch rzędach po trzy krążki. Przy każdym z krążków oprócz pierwszego krążka w drugim rzędzie znajduje się parafka oznaczająca znak wyboru. Przy pierwszym krążku z drugiego rzędu znajduje się krzyżyk na czerwonym tle. Pomiędzy drugim krążkiem z pierwszego rzędu a pierwszym krążkiem z drugiego rzędu oraz pomiędzy pierwszym i drugim i krążkiem z drugiego rzędu znajduje się linia przerywana.

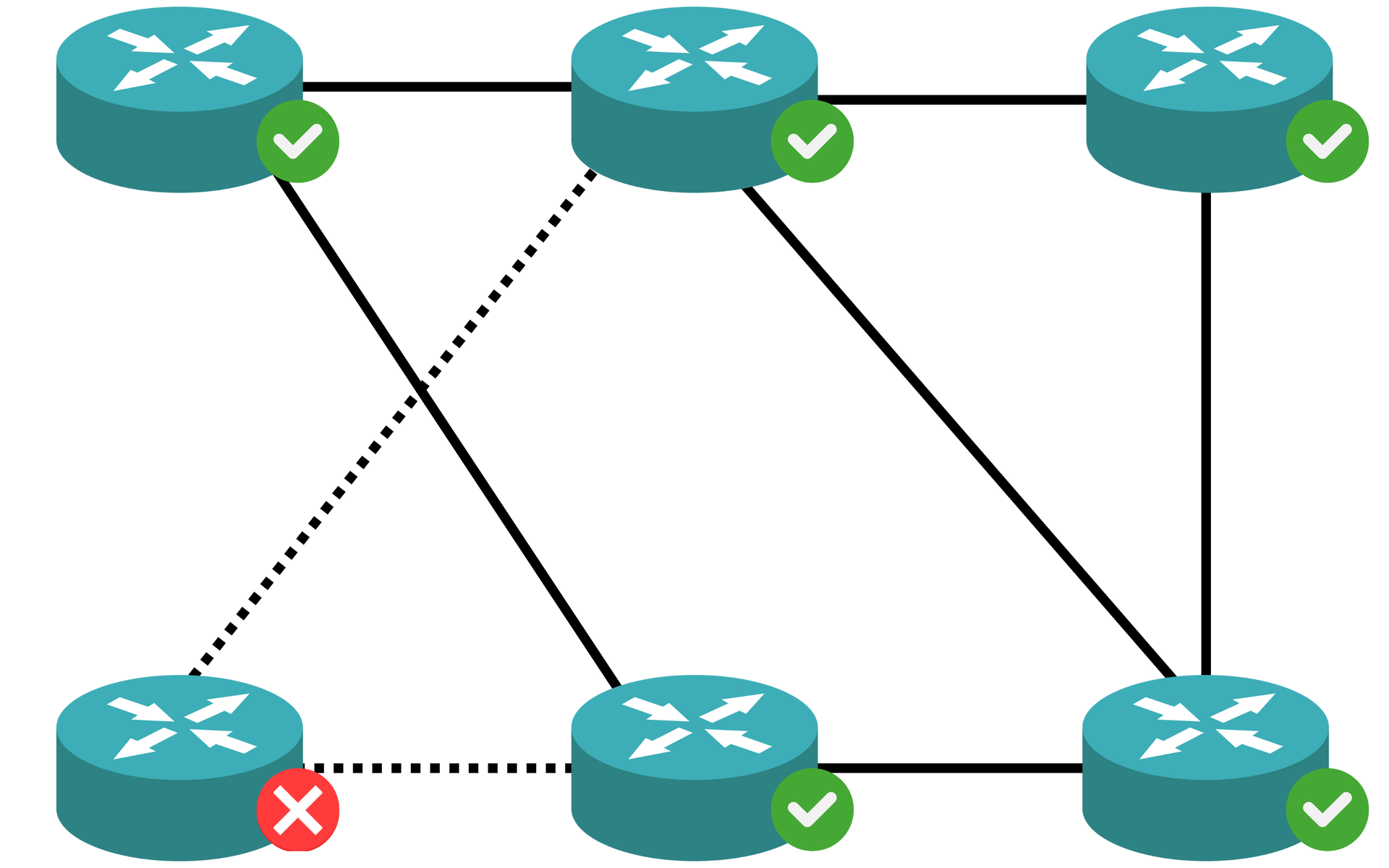
Połączenie dwóch routerów kanałem jest obarczone pewnym kosztem. Dla uproszczenia przyjmiemy, że utworzenie każdego połączenia kosztuje tyle samo. Chcemy przy możliwie najmniejszym koszcie stworzyć sieć, która spełnia minimalną niezawodnośćminimalna niezawodnośćminimalną niezawodność. Innymi słowy, chcemy utworzyć graf o spójności krawędziowej $k$ przy najmniejszej możliwej liczbie krawędzi. O ile określenie algorytmu, którego zadaniem byłoby zaprojektowanie takiej sieci, jest skomplikowanym zadaniem, o tyle możemy zbadać niezawodność już zaprojektowanej sieci.

Algorytm wyznaczania niezawodności sieci bada spójność krawędziową grafu. Na początku każdą nieskierowaną krawędź grafu zamienia się na dwie przeciwnie skierowane krawędzie o przepustowości równej 1. Algorytm wyznacza maksymalny przepływ między każdą parą wierzchołków $s$ i $t$. Graf jest $k$-spójny krawędziowo, jeśli maksymalny przepływ między każdą parą wierzchołków jest nie mniejszy niż $k$. Wtedy spójność krawędziowa grafu jest najmniejszym wyznaczonym przepływem.

Słownik