Przeczytaj
Warto przeczytać
Model gazu doskonałego
Przyjmuje się następujące założenia definiujące gaz doskonały:
Gaz doskonały składa się z ogromnej liczby cząsteczek poruszających się zupełnie losowo - chaotycznie (Rys. 1.). Wszystkie kierunki ruchu cząsteczek są jednakowo prawdopodobne, zaś ich zderzenia wzajemne lub zderzenia ze ściankami naczynia możemy opisywać stosując zasady dynamiki Newtona.
Cząsteczki gazu traktujemy, jak identyczne punkty materialnepunkty materialne. Rozmiary cząsteczek są zaniedbywalnie małe w porównaniu ze średnimi odległościami między cząsteczkami.
Zderzenia cząsteczek są sprężyste i krótkotrwałe. W zderzeniach spełnione są zasady zachowania energii kinetycznej i pędu.
Poza zderzeniami cząsteczki nie oddziałują ze sobą. Zakładamy, że zasięg sił oddziaływania międzycząsteczkowego jest mały w porównaniu z odległościami między cząsteczkami. Oznacza to, że pomiędzy zderzeniami cząsteczki poruszają się ruchem jednostajnym prostoliniowym.

W warunkach normalnych, w jednym centymetrze sześciennym gazu mieści się około N=1019 cząsteczek. Jest to niewyobrażalnie wielka liczba, która sprawia, że nawet przy użyciu najbardziej wydajnych, współczesnych komputerów bezpośredni opis ruchu każdej z tych cząsteczek z osobna jest niemożliwy. Tak naprawdę, bezpośredni opis nie byłby łatwy już przy N=10 cząsteczkach (lewa strona rysunku), byłby dość trudny przy N=300 cząsteczkach (prawa strona rysunku), a liczby N=1019 nie będziemy nawet komentować. To dlatego w opisie termodynamicznych własności gazów stosuje się metody statystyczne, które posługują się wartościami średnimi takimi, jak średnia prędkość cząsteczki, jej średnia energia kinetyczna itp.
Opis taki oferuje właśnie kinetyczno molekularna teoria gazów.
Teoria kinetyczno‑molekularna gazu doskonałego opisuje gaz doskonały na poziomie mikroskopowym, czyli zajmuje się poszczególnymi cząsteczkami, z których składa się gaz, ale ten opis ma charakter statystyczny (Rys. 1.)
Od czego zależy ciśnienie wywierane przez gaz na ścianki naczynia?
Wyobraźmy sobie gaz umieszczony w naczyniu. Jak to się dzieje, że gaz będący zbiorem cząsteczek wywiera ciśnienie na ścianki naczynia? Zgodnie z definicją, ciśnienie gazu to siła, z jaką gaz działa na jednostkową powierzchnię. Skąd bierze się ta siła?
Rozważmy pojedynczą cząsteczkę gazu, którą będziemy nazywali -tą cząsteczką (ta nazwa pochodzi od numeru cząsteczki, który może być równy , gdzie to liczba cząsteczek w zadanej objętości; mówiąc o -tej cząsteczce, a nie o pierwszej, drugiej, czy setnej, zaznaczamy, że zajmujemy się pewną losowo wybraną cząsteczką). Gdy taka cząsteczka zderza się ze ścianką naczynia, przy odbiciu od niej, w bardzo krótkim przedziale czasu , doznaje zmiany wektora pędu . Zgodnie z drugą zasadą dynamiki, zmiana pędu ciała (tutaj cząsteczki gazu) jest spowodowana tym, że podczas zderzenia ścianka działa na cząsteczkę siłą równą: . Z trzeciej zasady dynamiki wynika zaś to, że jeśli ścianka działa na cząsteczkę pewną siłą, to cząsteczka też działa na ściankę siłą, równą co do wartości, lecz przeciwnie skierowaną:
W ten oto sposób odpowiedzieliśmy na pytanie: Skąd w gazie bierze się siła, która powoduje powstanie ciśnienia. Nie pozostaje nam nic innego, jak wyznaczyć wartość tej siły.
Każda cząsteczka gazu, zderzając się ze ścianką, działa na nią pewną siłą.

Aby wyznaczyć siłę , z jaką podczas pojedynczego zderzenia -ta cząsteczka działa na ściankę naczynia zbadamy, co się dzieje z pędem cząsteczki podczas takiego zderzenia. Załóżmy, że cząsteczka ma masę , a jej chwilowa prędkość przed zderzeniem , tworzy kąt ze ścianką naczynia (Rys. 2.). Dalej, dla uproszczenia, będziemy analizować dwuwymiarową, a nie trójwymiarową, cząsteczkę. Będziemy też zakładać, że zderzenie ma charakter idealnie sprężysty (prędkość cząsteczki po zderzeniu ma taką samą wartość, jak przed zderzeniem ), a ścianki naczynia są idealnie gładkie (kąt padania jest równy kątowi odbicia). Czy patrząc na Rys. 2., dostrzegasz, że w wyniku zderzenia zmienił się kierunek wektora prędkości , a konkretnie:
prostopadła do ścianki składowa wektora prędkości zmieniła znak na przeciwny: , zaś
równoległa do ścianki składowa prędkości pozostała taka sama: .
Innymi słowy, w wyniku zderzenia ze ścianką wektor prędkości cząsteczki zmienił się w następujący sposób:
gdzie . Zmienił się też pęd cząsteczki:
Podsumowując, podczas pojedynczego zderzenia ze ścianką, siła z jaką cząsteczka działa na ściankę jest równa (por. równ. (1)):
Siła ta jest prostopadła do ścianki i ma wartość:
To jeszcze nie jest koniec obliczeń. Aby wyznaczyć ciśnienie gazu trzeba jeszcze oszacować, ile razy w czasie badana cząsteczka uderzyła w ściankę naczynia.

Aby oszacować tę liczbę (tj. ) rozważmy naczynie w kształcie kuli, o promieniu i objętości . Na Rys. 3. czerwoną linią zaznaczono tor cząsteczki w takim naczyniu. Zauważmy, że podczas każdego zderzenia ze ścianką naczynia, kąt padania i odbicia są takie same, a między kolejnymi zderzeniami cząsteczka zawsze przebywa taką samą odległość, równą:
Oznacza to, że w czasie , gdy przebywa ona drogę równą:
średnia liczba jej zderzeń ze ściankami naczynia wynosi
Znając (8) oraz (5) możemy obliczyć, z jaką siłą -ta cząsteczka działa na ścianki naczynia w przedziale czasu . Wartość tej prostopadłej do ścianek naczynia siły jest równa:
Wartość siły od wszystkich cząsteczek gazu jest natomiast równa:
Jeśli sumę kwadratów prędkości wszystkich cząsteczek podzielimy przez ich liczbę, otrzymamy średni kwadrat prędkości cząsteczek:
Pierwiastek z wyrażenia nazywamy prędkością średnią kwadratową i oznaczamy :
Korzystając z powyższego oznaczenia, wyrażenie (10) na wartość siły, jaka w jednostce czasu działa na ścianki kulistego naczynia, można zapisać w uproszczonej postaci:
Dzieląc tę siłę przez pole powierzchni kuli otrzymamy ciśnienie, jakie cząsteczki gazu wywierają na ścianki naczynia:
W końcu, podstawiając w ostatnim wyrażeniu dostajemy jeden z najważniejszych wzorów teorii kinetyczno‑molekularnej gazu doskonałego:
Wynik (15) zasługuje na uwagę, ponieważ łączy on bezpośrednio mierzalne wielkości makroskopowe opisujące gaz (tzn. ciśnienie gazu , jego objętość oraz masę ) z wielkościami mikroskopowymi charakteryzującymi pojedyncze cząsteczki gazu (mowa o prędkości średniej kwadratowej: ).
Prędkość średnia kwadratowa.
Prędkość średnią kwadratową cząsteczek gazu doskonałego można wyznaczyć za pomocą równania (15):
gdzie jest całkowitą masą gazu. Pamiętając o tym, że stosunek masy do objętości definiuje gęstość: , wzór (16) można również przepisać w postaci:
Jak widzimy, prędkość średnia kwadratowa zależy od ciśnienia i gęstości gazu. Okazuje się, że dla typowo spotykanych gazów (np. składników powietrza), w warunkach zbliżonych do normalnych, prędkość ta jest rzędu setek m/s, a więc znacznie przewyższa ona prędkości spotykane na co dzień.
Średnia energia kinetyczna cząsteczek gazu, a jego temperatura termodynamiczna
Na koniec zastanówmy się, jakie jeszcze wnioski można wyciągnąć z wyrażenia (15). Zauważmy, że jeśli licznik i mianownik prawej strony równ. (15) pomnożymy przez 2, to otrzymamy:
W powyższym wyrażeniu, drugi z czynników mamy prawo nazwać średnią energią kinetyczną cząsteczek gazu. Zależność (15) możemy zatem zapisać w postaci:
Zauważamy podobieństwo tej zależności do równania Clapeyrona:
będącego równaniem stanu gazo doskonałego. W powyższym równaniu oznacza temperaturę w skali Kelwina, - liczbę moli gazu, zaś jest stałą gazową.
Przywołane tu równanie Clapeyrona jest związkiem wyprowadzonym empirycznie, poprzez uogólnienie faktów doświadczalnych. Oznacza to, że wyniki dotyczące interpretacji temperatury, które dalej otrzymamy, są uzupełnieniem teorii kinetyczno‑molekularnej gazu doskonałego, a nie jej częścią.
Porównując prawe strony wyrażeń (19) i (20) i dostajemy:
Z ostatniej zależności możemy wyznaczyć średnią energię kinetyczną cząsteczek w zależności od temperatury:
Liczbę cząsteczek możemy zapisać jako iloczyn liczby moli i liczby cząsteczek w 1 molu gazu (liczby Avogadro), . Wzór (22) przybierze wówczas postać:
We wzorze tym występują dwie stałe: stała gazowa i liczba Avogadro . Ich iloraz definiuje tzw. stałą Boltzmanna:
Średnią energię kinetyczną w ruchu postępowym, przypadającą na jedną cząsteczkę gazu, możemy wobec tego przedstawić jako
Wzór (25) pokazuje, czym jest kolejny makroskopowy parametr – temperatura. To wielkość wprost proporcjonalna do średniej energii kinetycznej cząsteczek w ich ruchu postępowym. Mówimy w skrócie, że temperatura jest miarą średniej energii kinetycznej cząsteczek (Rys. 4.). Dotyczy to jednak chaotycznego ruchu dużej liczby cząsteczek w układzie, w którym średnia suma ich pędów jest zerowa.
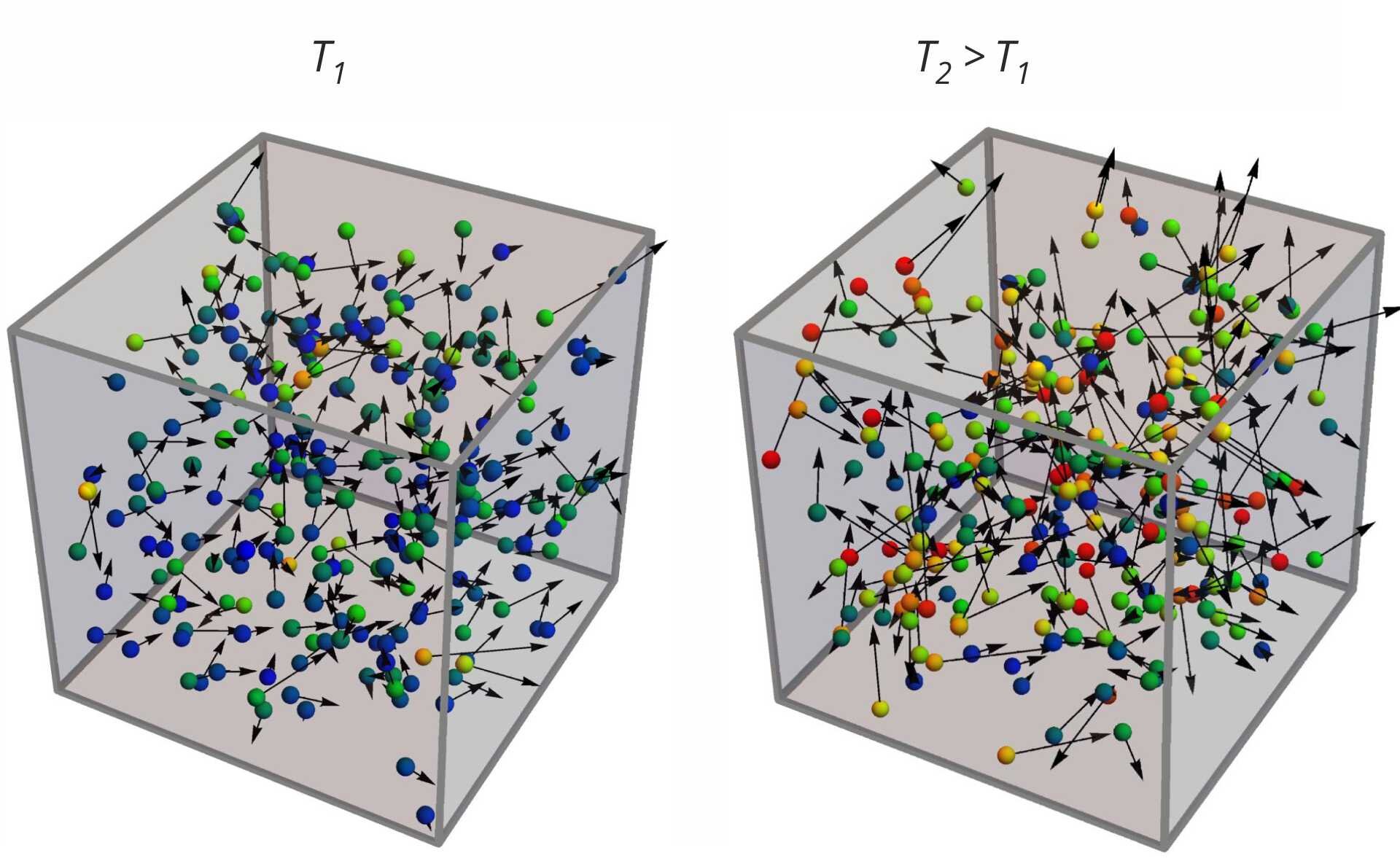
Cząsteczki o różnych masach
Obliczmy, dla przykładu, średnią energię kinetyczną i prędkość średnią kwadratową cząsteczek dwutlenku węgla i wodoru w temperaturze . Masa molowa wynosi: 44 g/mol, a dla jest równa: 2 g/mol.

Skorzystamy ze wzoru (25) na średnią energię kinetyczną cząsteczek w ich ruchu postępowym:
Jak widać, średnia energia kinetyczna cząsteczek nie zależy od rodzaju gazu i jest jednakowa dla różnych gazów w jednakowej temperaturze.
Aby obliczyć prędkość średnią kwadratową cząsteczek, użyjemy wzoru:
skąd mamy
Masa jednej cząsteczki gazu to masa 1 mola podzielona przez liczbę Avogadro .
Masa cząsteczki wodoru wynosi zatem: , stąd jej prędkość średnia kwadratowa
Analogicznie dla cząsteczki dwutlenku węgla: , więc
Z obliczeń tych wynika, że w danej temperaturze średnie energie kinetyczne cząsteczek różnych gazów są jednakowe, ale ich prędkości średnie kwadratowe różnią się, jeśli różne są ich masy molowe. Im większa więc masa cząsteczki, tym mniejsza prędkość średnia kwadratowa.
Czy te obliczenia są właściwe?
To pytanie jest uzasadnione! Założyliśmy przecież, że cząsteczki gazu traktujemy jak identyczne punkty materialne. Wiemy jednak, że cząsteczki wodoru i dwutlenku węgla składają się z atomów, odpowiednio, wodoru oraz węgla i tlenu (Rys. 5.). Mają więc wewnętrzną strukturę. Okazuje się, że otrzymane przez nas wyniki są w dobrym przybliżeniu poprawne, choć strukturę cząsteczek trzeba bez wątpienia uwzględnić przy opisywaniu energii wewnętrznej gazu.
Składa się na nią nie tylko energia kinetyczna w ruchu postępowym cząsteczek, ale także inne formy energii, jak energia kinetyczna ich ruchu obrotowego. Choć ciśnienie wywierane przez gaz zależy tylko od tej pierwszej formy energii, to pozostałe mogą się objawiać przy wymianie energii pomiędzy gazem a otoczeniem. Więcej o tych zagadnieniach możesz przeczytać w e‑materiale „Jaki jest związek pomiędzy temperaturą w skali Kelvina a średnią energią ruchu cząsteczek gazu doskonałego i jego energią wewnętrzną?”.
Słowniczek
(ang.: internal energy) suma wszystkich rodzajów energii, kinetycznych i potencjalnych, cząsteczek i atomów tworzących dany układ. Dla gazu doskonałego energia wewnętrzna zależy tylko od temperatury i liczby cząsteczek.
(ang.: point‑like mass) inaczej zwana punktem meterialnym, to ciało fizyczne obdarzone masą, ale mające nieskończenie małe rozmiary (będące punktem). W mechnice tzw. „przybliżenie punktu materialnego” bardzo upraszcza opis ruchu ciała.
(ang: ideal gas law, general gas equation) równanie stanu gazu doskonałego. Jest to matematyczny związek pomiędzy ciśnieniem, objętością i temperaturą gazu doskonałego, o postaci:
Równanie to wyprowadził w roku 1834 francuski fizyk Benoît Emile Clapeyron, uogólniając dotychczasową wiedzę eksperymentalną o zachowaniu się gazów.