Przeczytaj
W tej lekcji zajmiemy się prostymi równoległymi do osi , czyli, przy tradycyjnym położeniu układu współrzędnych, prostymi poziomymi.
Naszkicujemy w układzie współrzędnych zbiór wszystkich punktów , które spełniają równanie:
a) ,
b) ,
c) .
Zwróćmy uwagę, że w tym równaniu w ogóle nie występuje zmienna . Oznacza to, że wartość jest równa 3 niezależnie od tego, ile jest równy . Zatem może przyjmować dowolną wartość. Zilustrujemy to zjawisko tabelką:
Podsumowując, równanie spełniają na przykład punkty , , , , .
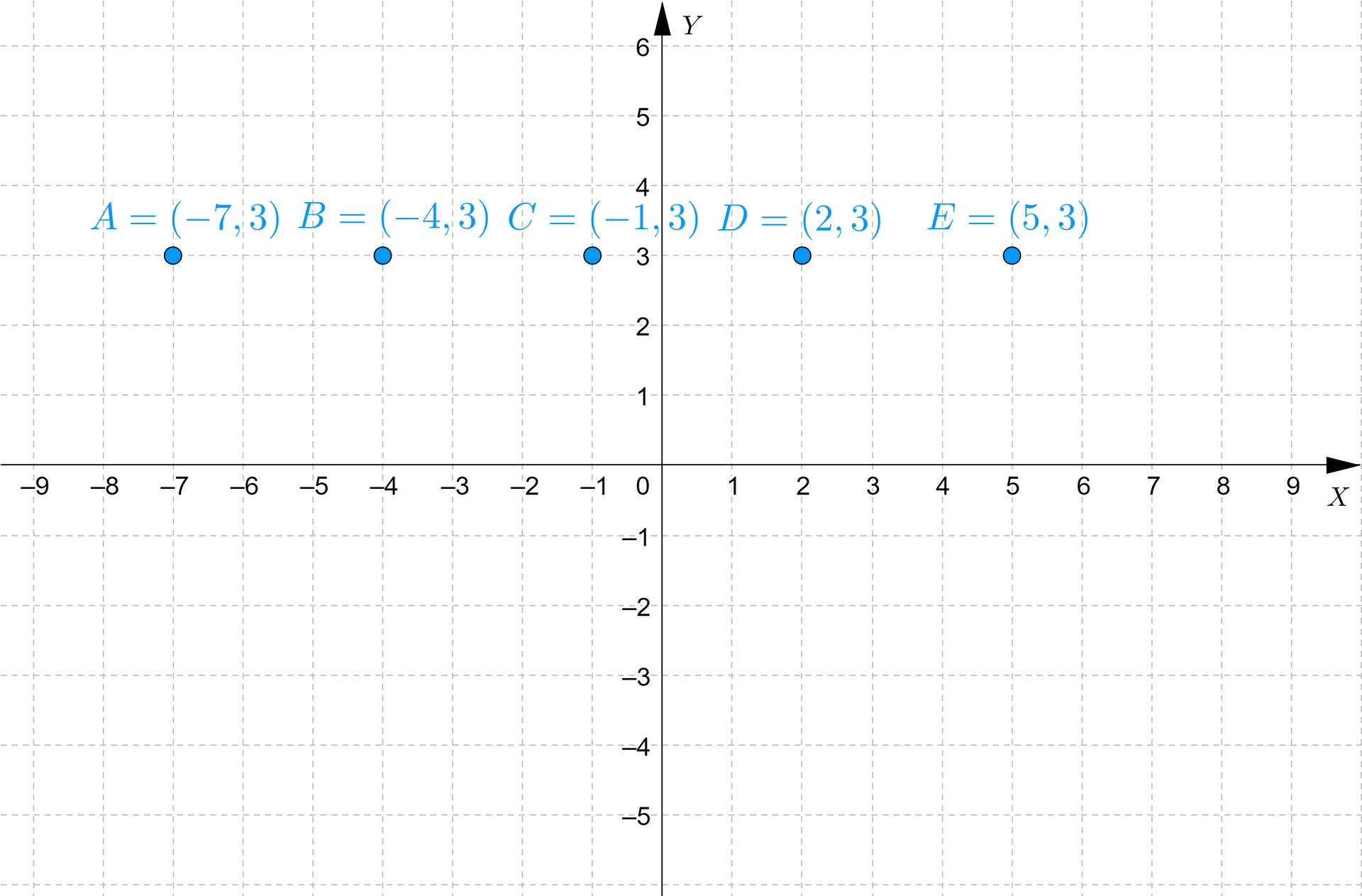
Zauważmy, że po zaznaczeniu ich w układzie współrzędnych układają się one wzdłuż prostejprostaprostej o równaniu .

W tym równaniu również nie występuje zmienna . Oznacza to, że dla dowolnego wartość zmiennej zawsze równa będzie . Możemy tę zależność zilustrować tabelką:
Zwróćmy jeszcze uwagę, że liczby wybraliśmy zupełnie losowo. Równanie jest spełnione przez punkty , , , , .

Po zaznaczeniu ich w układzie współrzędnych możemy przez nie poprowadzić prostą o równaniu .

W tym równaniu również nie występuje zmienna , więc wartość jest równa 0, niezależnie od wartości . Zilustrujmy to tabelką:
A zatem równanie jest spełnione przez punkty , , , , .
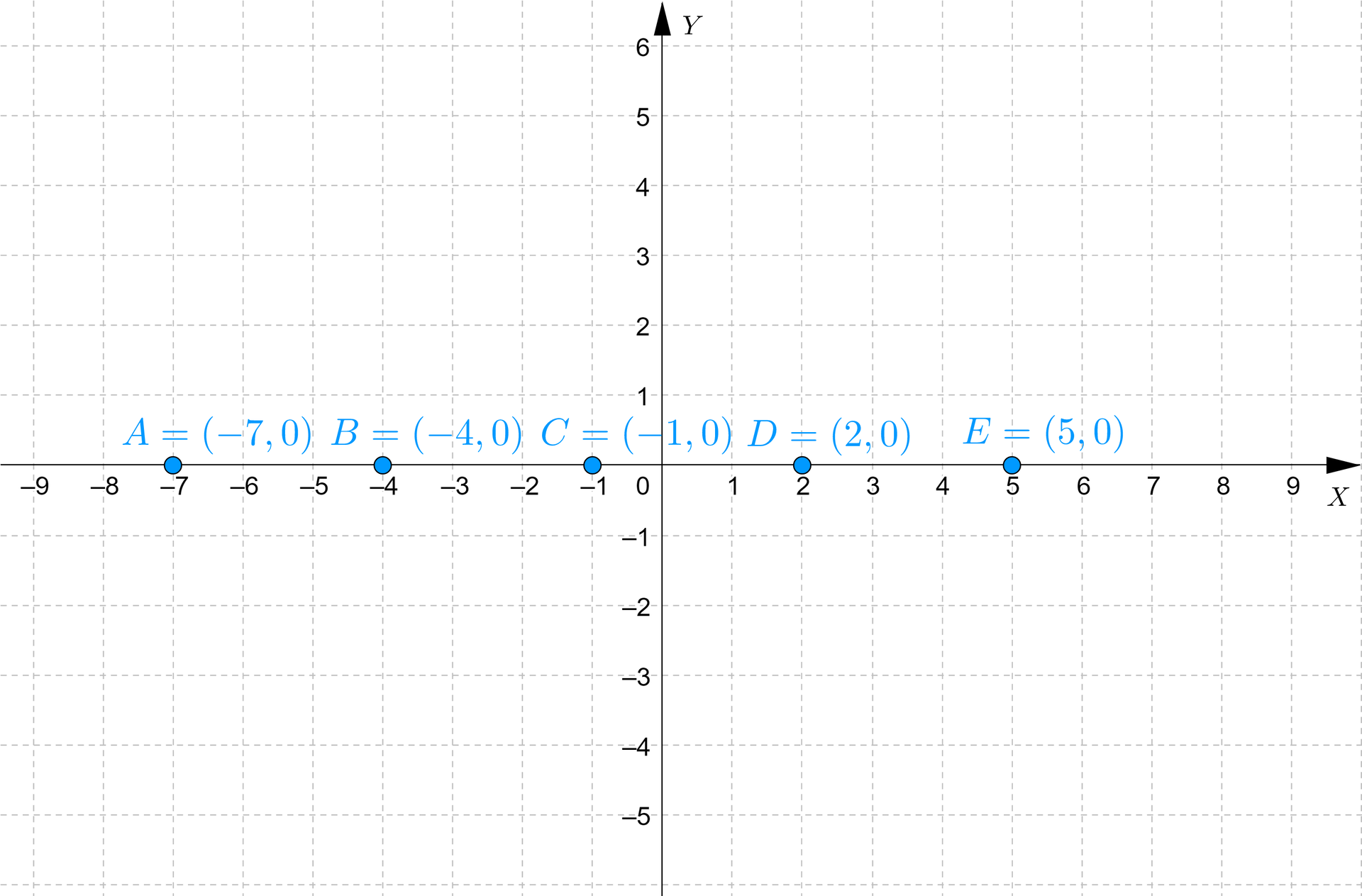
Po zaznaczeniu ich w układzie współrzędnych możemy poprowadzić prostą o równaniu .

Wniosek
Zbiór wszystkich punktów spełniających równanie ilustruje w układzie współrzędnych prostą równoległą do osi .
W prostokątnym układzie współrzędnych narysujmy zbiór punktów spełniających podane równanie:
a) ,
b) ,
c) .
Aby naszkicować wykres tego równania, możemy skorzystać z definicji wartości bezwzględnej. Mianowicie wprost z niej wynika, że równanie jest spełnione gdy lub . Pierwsze współrzędne punktów mogą być dowolne. Zatem wykresem równania jest suma dwóch prostych o równaniach , .
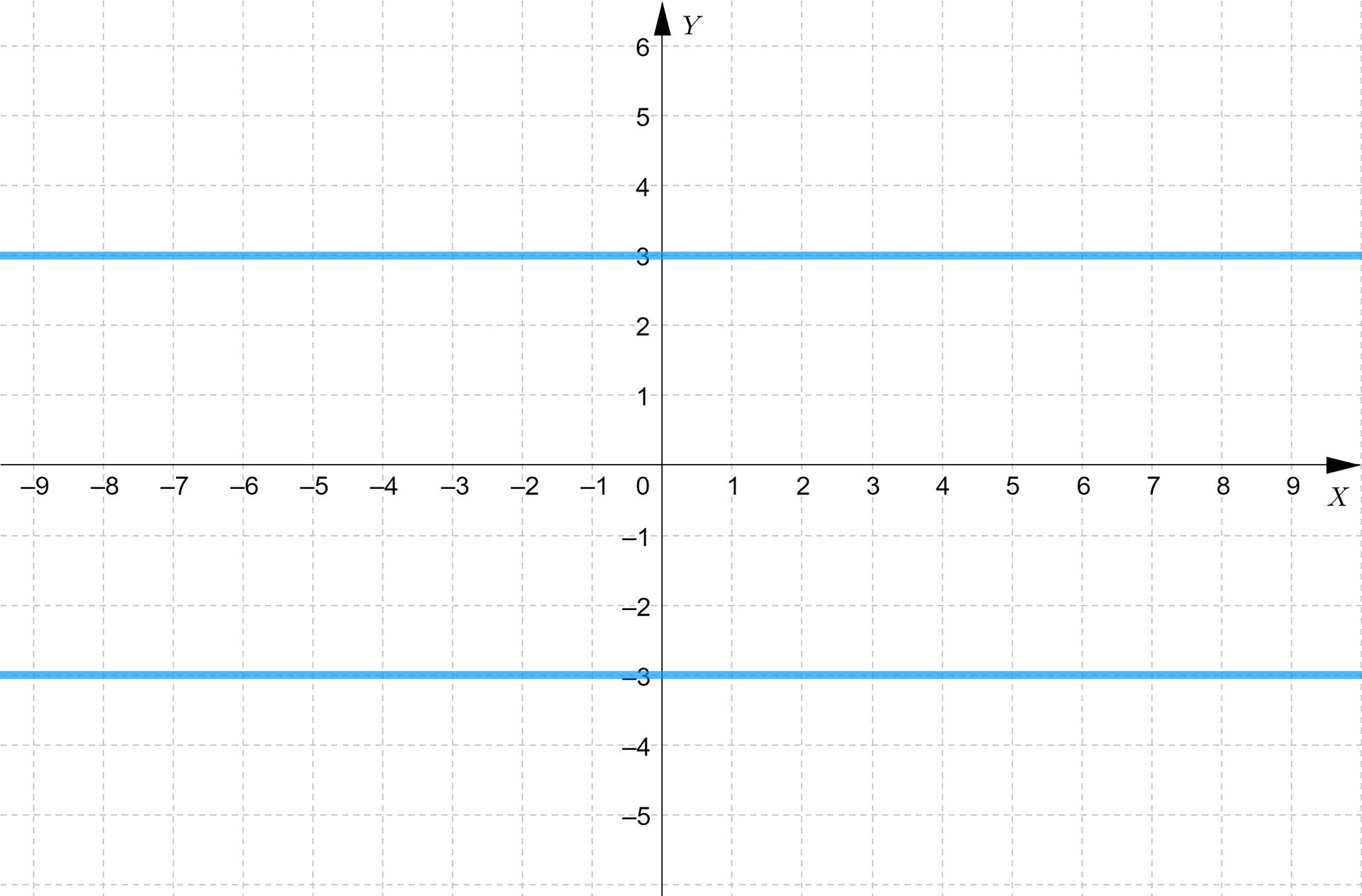
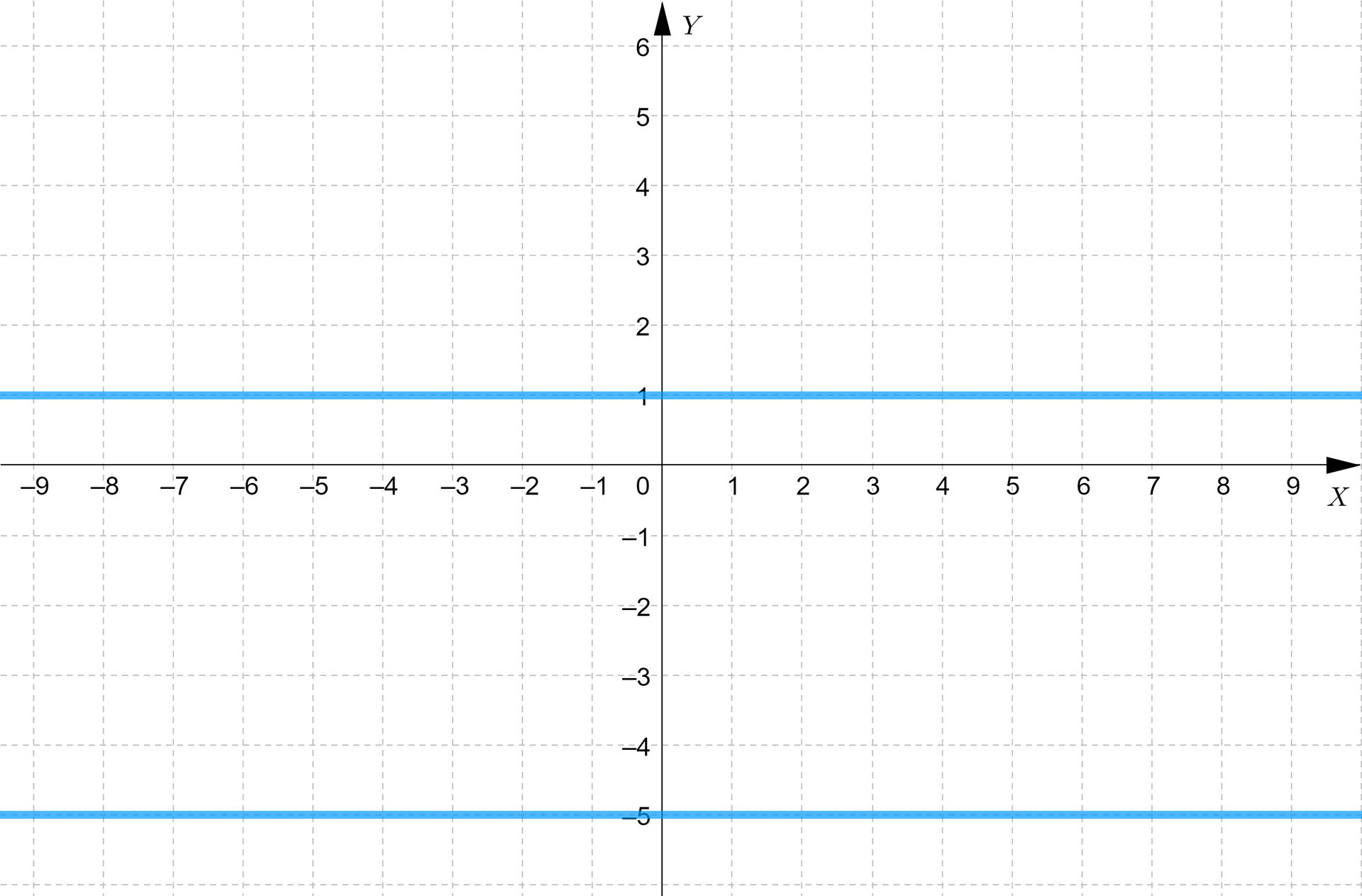
Aby zaznaczyć w układzie współrzędnych zbiór punktów spełniających równania , można skorzystać z interpretacji geometrycznej. Przypomnijmy, że wartość bezwzględna liczby to jej odległość od zera na osi liczbowej. Zatem zbiorem punktów, których współrzędne spełniają równanie są te punkty, które oddalone są od osi o odległość . Punkty te tworzą dwie proste równoległe do osi odległe od niej o jednostki, co możemy zobaczyć na powyższej ilustracji. Proste te mają wzory: oraz .
Aby naszkicować wykres tego równania możemy skorzystać z definicji wartości bezwzględnej. Wprost z definicji wynika, że równanie jest spełnione gdy lub . Czyli równoważnie lub . Pierwsze współrzędne punktów należących do opisanego zbioru mogą być dowolne. Zatem wykresem równania jest suma dwóch prostych o równaniach , .
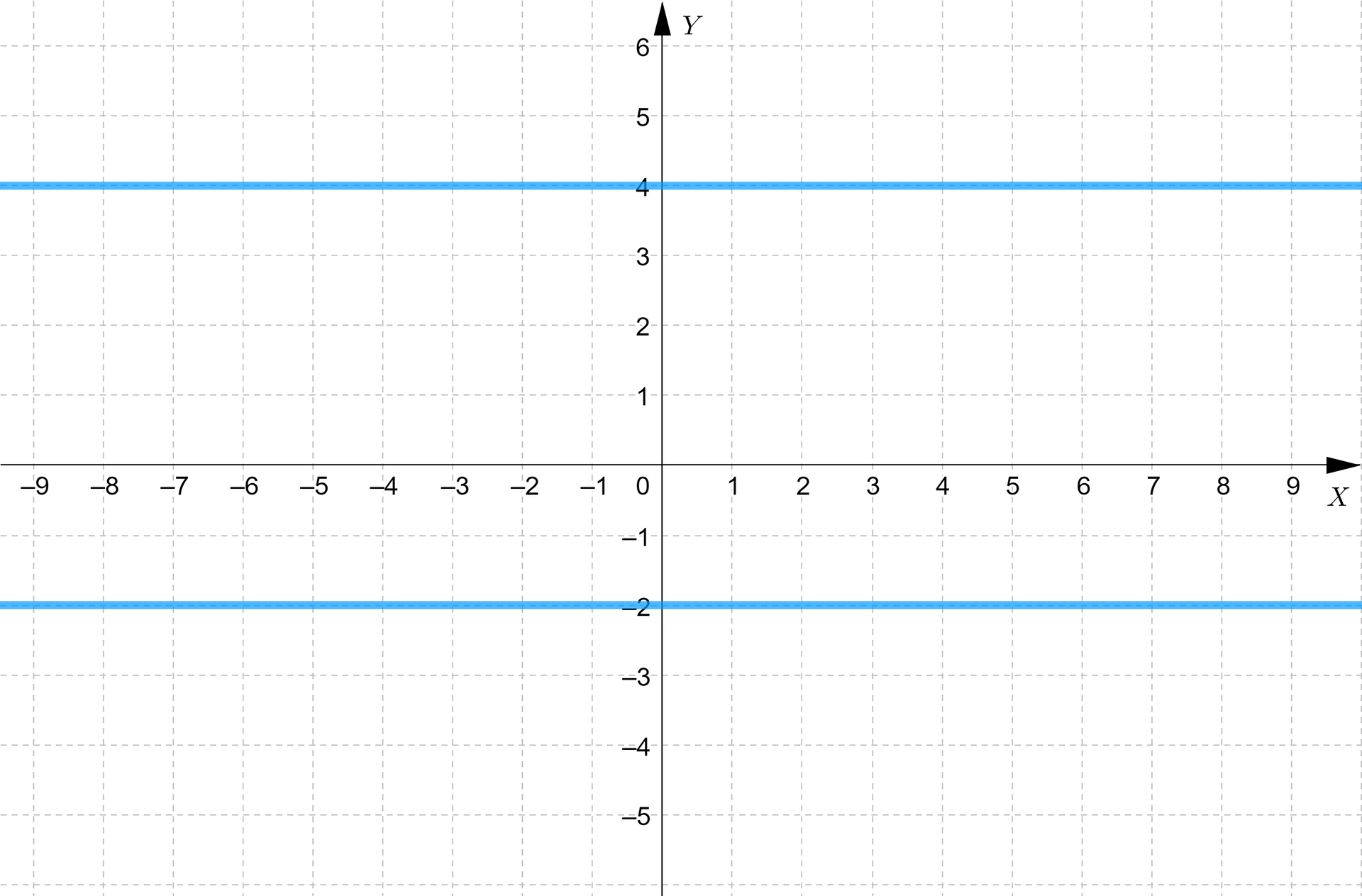
Korzystając z interpretacji graficznej możemy stwierdzić, że interesują nas wszystkie punkty , dla których pierwsza współrzędna jest dowolna, zaś druga jest liczbą, której odległość od jedynki jest równa . W odległości od liczby leżą liczby oraz .
Aby naszkicować wykres tego równania możemy skorzystać z definicji wartości bezwzględnej, z której wynika, że równanie jest spełnione gdy lub . Czyli równoważnie lub . Pierwsze współrzędne punktów mogą być dowolne. Zatem wykresem równania jest suma dwóch prostych o równaniach , .
Znając równania prostychprostaprostych równoległych do osi , możemy opisywać też obszary ograniczone tymi prostymiprostaprostymi. Do ich opisu posłużymy się nierównościami, również z wartościami bezwzględnymi.
Naszkicuj zbiory punktów opisane przez poniższe nierówności:
a) ,
b) ,
c) ,
d) .
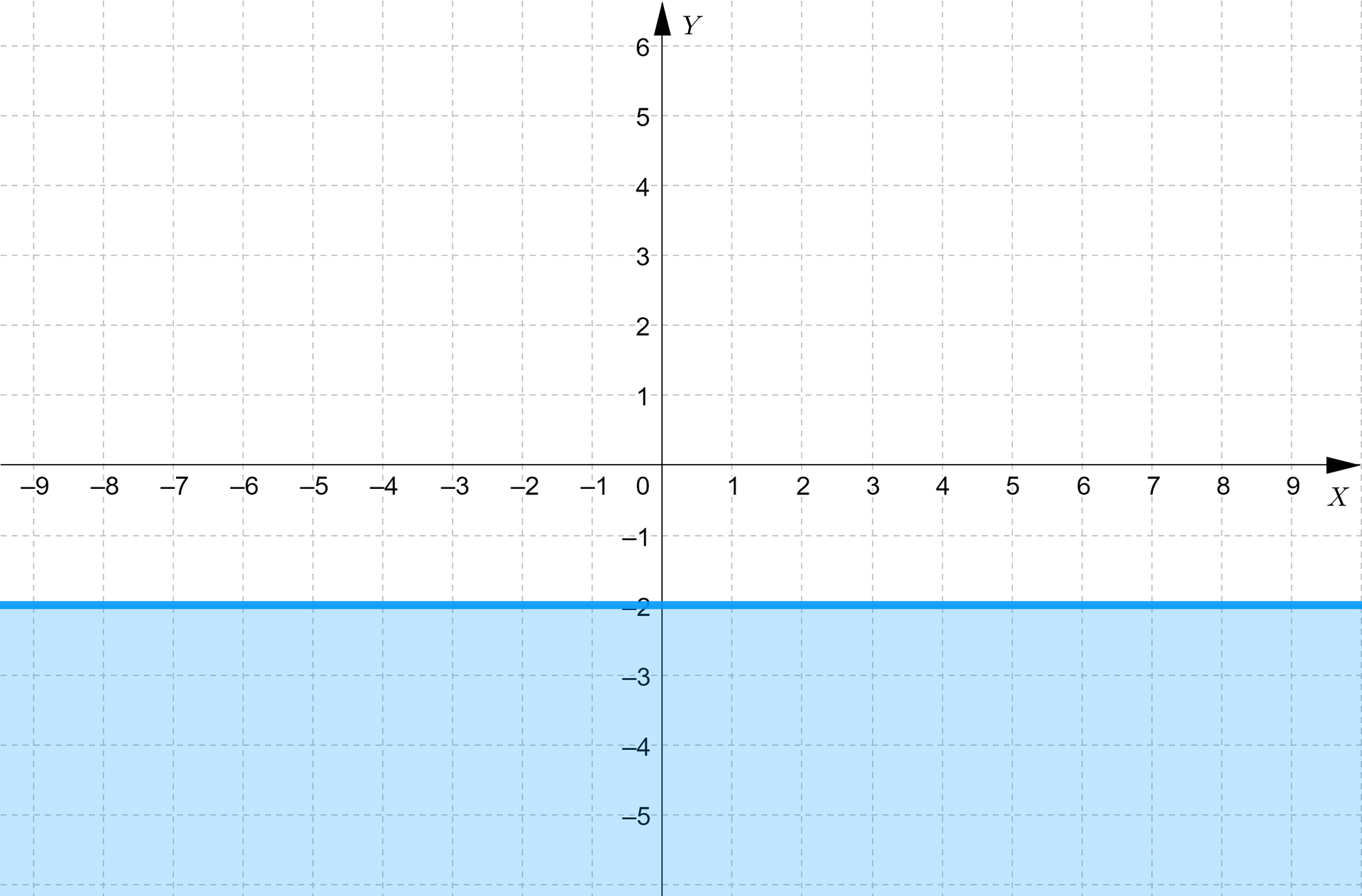
W obszarze naszych zainteresowań tym razem znalazły się wszystkie punkty , których współrzędna jest dowolną liczbą rzeczywistą, zaś druga jest większa od . Zatem w układzie współrzędnych zaznaczymy wszystkie punkty, które leżą ponad prostą o równaniu , ale bez tej prostej. Dla podkreślenia, że punkty należące do tej prostej nie należą do szukanego przez nas obszaru, będziemy rysować ją linią przerywaną.

Tym razem interesują nas wszystkie punkty , których współrzędna jest dowolną liczbą rzeczywistą, zaś druga jest niemniejsza (większa lub równa) od . Zatem w układzie współrzędnych zaznaczymy wszystkie punkty, które leżą ponad prostą o równaniu lub na tej prostej. Dlatego ta prosta będzie narysowana linią ciągłą.

Tym razem interesują nas wszystkie punkty , których współrzędna jest dowolną liczbą rzeczywistą, zaś jest liczbą mniejszą od . Zatem w układzie współrzędnych zaznaczymy:

Tym razem interesują nas wszystkie punkty , których współrzędna jest dowolną liczbą rzeczywistą, zaś jest liczbą niewiększą (mniejszą lub równą) od . Zatem w układzie współrzędnych zaznaczymy wszystkie punkty, które leżą pod prostą o równaniu lub na tej prostej. Dlatego ta prostaprostaprosta będzie narysowana linią ciągłą.
Naszkicujemy zbiory punktów opisane przez poniższe nierówności z wartościami bezwzględnymi.
a) ,
b) ,
c) ,
d) .
Zauważmy najpierw, że współrzędna każdego punktu zbioru opisanego przez nierówność może być dowolną liczbą. Z własności wartości bezwzględnej wynika, że . W praktyce oznacza to, że szukany obszar jest zawarty pomiędzy prostymi o równaniach i , ale żadna z tych prostych nie należy do tego obszaru – dlatego będą narysowane liniami przerywanymi.

Równoważnie moglibyśmy skorzystać z interpretacji geometrycznej wartości bezwzględnej. Mianowicie nierówność oznacza wszystkie liczby , których odległość od zera na osi jest mniejsza od . Zatem będą to liczby . Współrzędna nadal może być dowolną liczbą rzeczywistą.
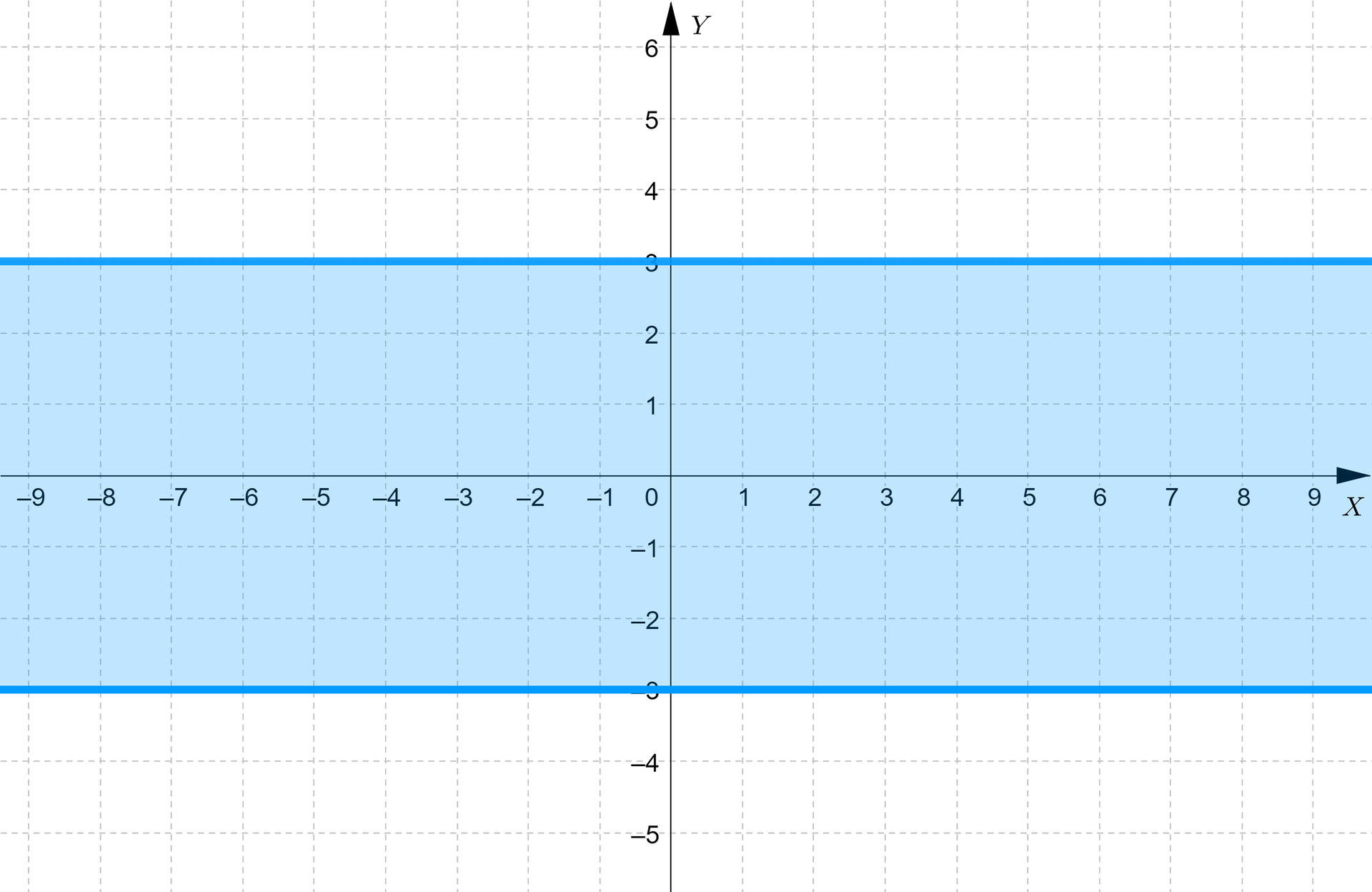
Tym razem nierówność możemy przedstawić równoważnie jako nierówność podwójną . Ponieważ pierwsza współrzędna szukanych punktów może być dowolna, zatem interesuje nas obszar pomiędzy prostymi o równaniach i wraz z tymi prostymi. Z interpretacji geometrycznej wynika, że nierówność to zbiór wszystkich liczb , które leżą w odległości co najwyżej jednostek od zera na osi . Oczywiście oznacza to, że .
Tym razem nierówność możemy przedstawić jako alternatywę lub . Współrzędna szukanych punktów może być dowolną liczbą rzeczywistą, zatem interesujące nas punkty, które leżą nad prostą o równaniu lub pod prostą o równaniu , ale nie należą do tych prostych.

Geometrycznie nierówność można zinterpretować jako zbiór wszystkich liczb , których odległość od zera na osi jest większa od . Zatem . Współrzędna szukanych punktów ponownie może przyjmować dowolną wartość.
Tym razem nierówność możemy przedstawić jako alternatywę lub . Pierwsza współrzędna szukanych punktów może być dowolną liczbą, zatem interesujące nas punkty leżą nad prostą o równaniu lub pod prostą o równaniu , lub na tych prostych.
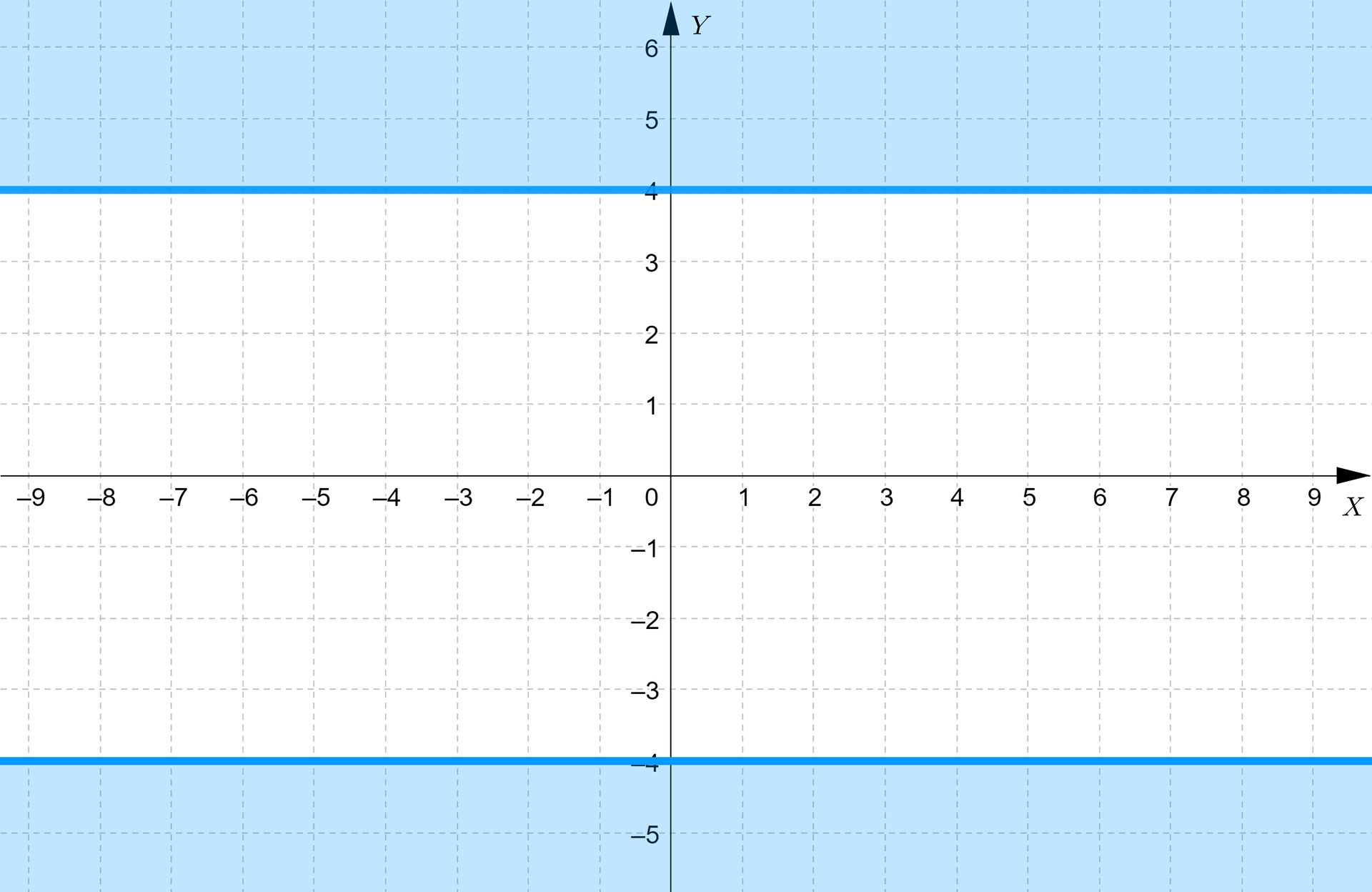
Geometrycznie nierówność można zinterpretować jako zbiór wszystkich liczb , których odległość od zera na osi jest niemniejsza od . Zatem . Współrzędna szukanych punktów ponownie może przyjmować dowolną wartość.
Naszkicujemy zbiory punktów opisane przez poniższe nierówności z wartościami bezwzględnymi.
a)
b)
Powyższa nierówność jest równoważna alternatywie nierówności lub , zatem równoważnie lub . Wobec tego interesujące nas punkty leżą ponad prostą o równaniu lub pod prostą o równaniu , ale nie na tych prostych, które w związku z tym rysujemy linią przerywaną.
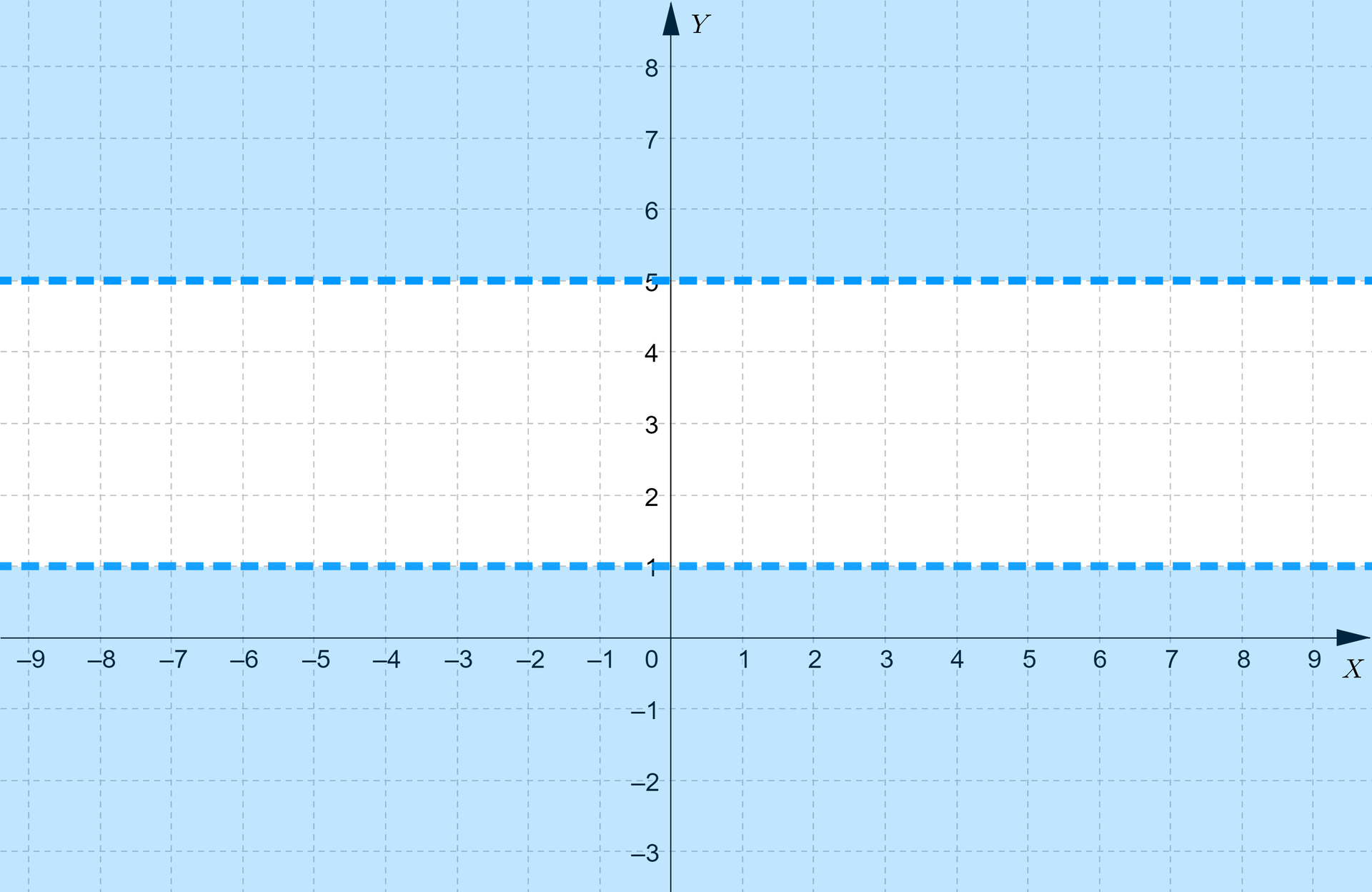
Geometrycznie nierówność można zinterpretować jako zbiór wszystkich liczb , których odległość od liczby trzy na osi jest większa od . Zatem . Współrzędna szukanych punktów ponownie może przyjmować dowolną wartość rzeczywistą.
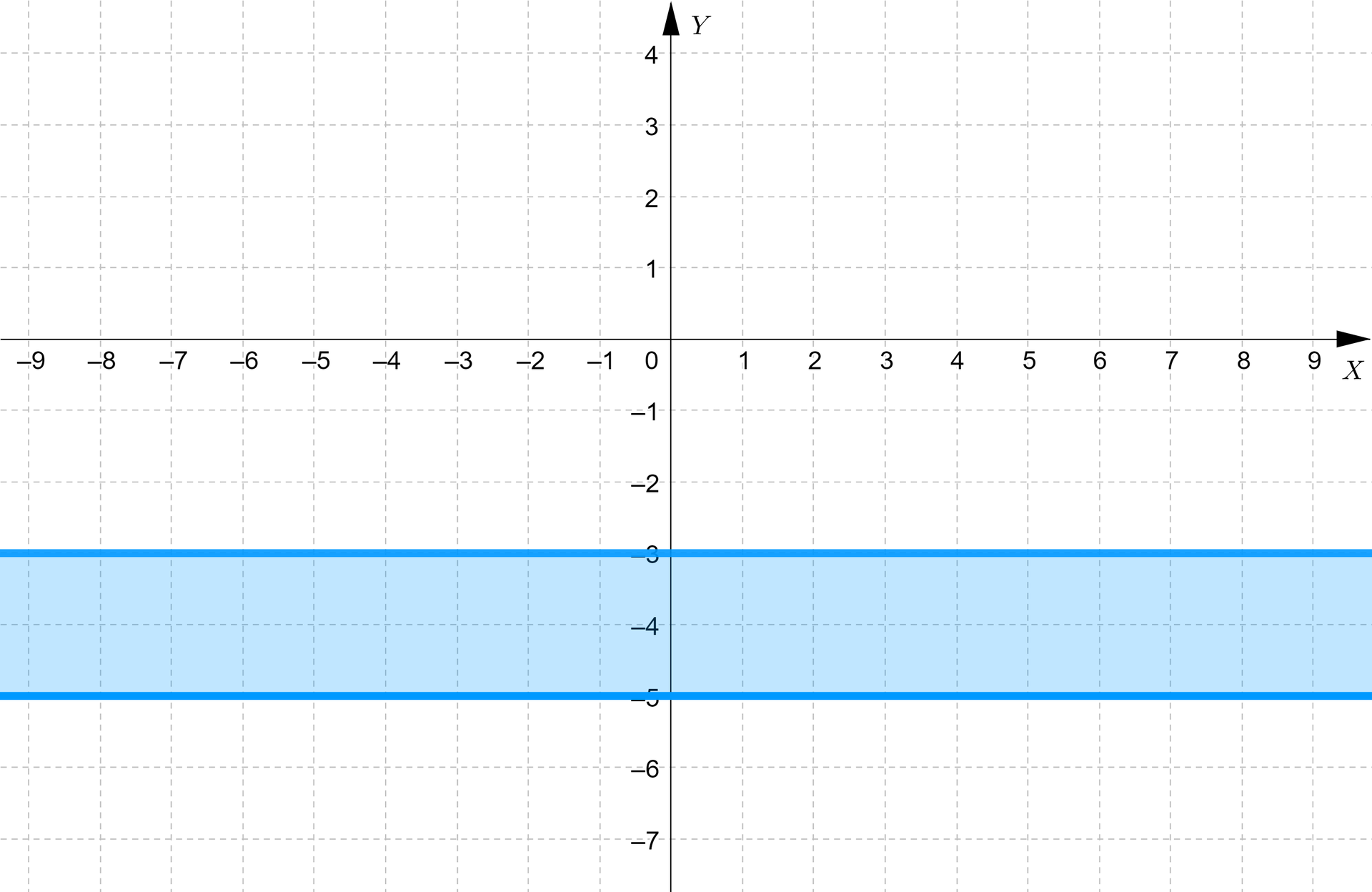
Powyższa nierówność jest równoważna nierówności podwójnej
Wobec tego interesujące nas punkty leżą pomiędzy prostymi o równaniach oraz lub na tych prostych. Linie oznaczające te proste rysujemy w sposób ciągły.
Słownik
w geometrii euklidesowej: pojęcie pierwotnepojęcie pierwotnepojęcie pierwotne;
w geometrii analitycznej: zbiór wszystkich punktów o współrzędnych , które spełniają równanie liniowe , przy założeniu, że i nie są jednocześnie zerami
to pojęcie na tyle intuicyjnie zrozumiałe i proste, że w danej teorii matematycznej nie wymaga definiowania lub jego zdefioniowanie nie jest możliwe; dzięki niemu można zdefiniować każde inne pojęcie, czyli każde pojęcie matematyczne, które nie jest pojęciem pierwotnym, musi zostać zdefiniowane