Systemy liczbowe są zbiorami reguł, według których zapisuje się liczby, a także je nazywa (odczytuje). Wykorzystywane są przy tym zestawy symboli (cyfr, liter albo innych znaków) specyficzne dla każdego systemu liczbowego.

Podstawowymi systemami liczbowymi są:

• system pozycyjny – w którym znaczenie ma pozycja zapisywanych cyfr. Każdej z nich odpowiada waga (zależna od miejsca zajmowanego przez cyfrę i od podstawy systemu). Najbardziej znanego systemu pozycyjnego uczymy się już w szkole podstawowej; mowa oczywiście o systemie dziesiętnym.

• system addytywny – w którym wartość liczby jest sumą wartości jej wszystkich cyfr. Przykładem takiej metody zapisywania liczb jest system rzymski.

Krótka historia zapisu liczb

Za pierwsze próby zapisywania liczb uchodzą żłobienia i nacięcia wykonywane w drewnie, kamieniu albo kościach. Można podejrzewać, że suma takich symboli oznaczała liczbę. Był to najprostszy sposób zapisu, ponieważ wykorzystywano tylko jeden znak (cyfrę) – pojedyncze nacięcie.

System egipski był systemem addytywnym, w którym kolejne potęgi liczby 10 przedstawiano za pomocą hieroglifów. Przykładowo, używając pojedynczej kreski zapisywano liczbę 1, symbol podkowy oznaczał 10, zaś liczba 100 000 była przedstawiona za pomocą rysunku żaby. Aby odczytać zapisaną liczbę należało dodać do siebie wartości odpowiadające poszczególnym symbolom. Liczby będące wielokrotnościami hieroglifów zapisywano powtarzając odpowiednie symbole do momentu uzyskania wymaganej sumy.

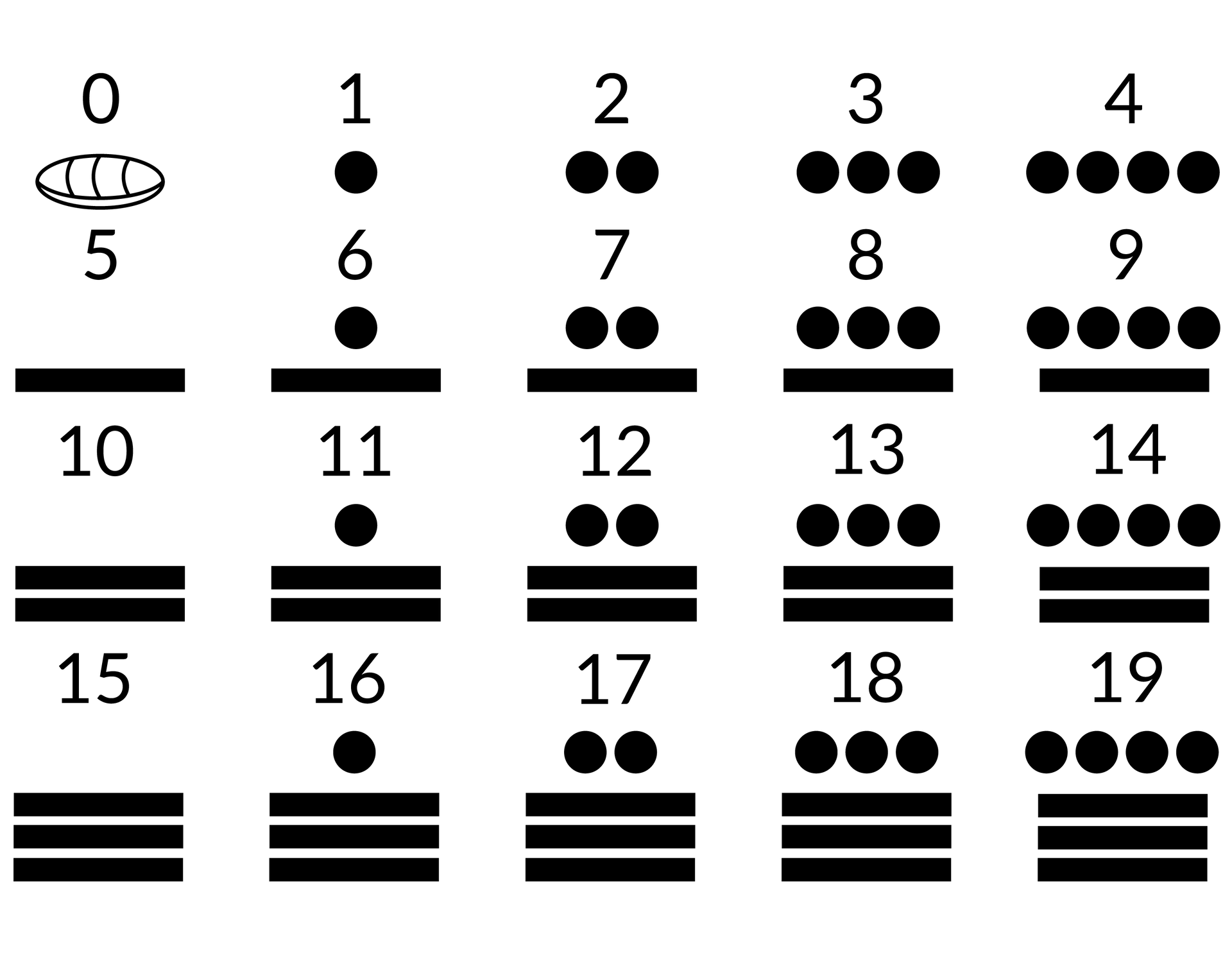
System Majów był pozycyjnym systemem o podstawie 20. Używano w nim trzech symboli: kropki, poziomej kreski oraz muszli. Majowie znali pojęcie zera i przedstawiali tę cyfrę za pomocą znaku muszli.

RkuLPkXqJLxuR

Na rysunku przedstawiono sposób zapisu dziewiętnastu cyfr. 0 za pomocą muszli. 1 za pomocą jednej kropki. 2 za pomocą dwóch kropek. 3 za pomocą trzech kropek. 4 za pomocą czterech kropek. 5 za pomocą poziomej kreski. 6 za pomocą jednej kropki nad poziomą kreską. 7 za pomocą dwóch kropek nad poziomą kreską. 8 za pomocą trzech kropek nad poziomą kreską. 9 się za pomocą czterech kropek nad poziomo kreską. 10 za pomocą dwóch poziomych kresek. 11 za pomocą kropki nad dwoma poziomymi kreskami. 12 za pomocą dwóch kropek na dwoma poziomymi kreskami. 13 za pomocą trzech kropek nad dwoma poziomymi kreskami. 14 za pomocą czterech kropek nad dwiema poziomymi kreskami. 15 za pomocą trzech poziomych kresek.1 6 za pomocą jednej kropki nad trzema poziomymi kreskami. 17 za pomocą dwóch kropek nad trzema poziomymi kreskami. 18 za pomocą trzech kropek nad trzema poziomymi kreskami. 19 za pomocą czterech kropek nad trzema poziomymi kreskami.

System sześćdziesiątkowy (babiloński) powstał w Mezopotamii ok. XVIII w. p.n.e. Jest on uznawany za pierwszy system pozycyjny. Nie wykorzystywano w nim symbolu zera, czego wynikiem były problemy z zapisywaniem niektórych liczb. W przypadku gdy na którejkolwiek pozycji nie był potrzebny znak sześćdziesiątkowy, pozostawiano odstęp między symbolami (we współczesnych systemach pozycyjnych znalazłaby się tam cyfra zero). Kłopot pojawiał się, gdy potrzebne były co najmniej dwa odstępy obok siebie, albo gdy puste miejsce miało się znaleźć na końcu. Prowadziło to do nieporozumień: przykładowo, liczbę 2 zapisywano tak samo jak 120 (2 razy 60). System babiloński stosujemy w ograniczonym zakresie do dzisiaj (godzina składa się z 60 minut, a minuta z 60 sekund; jedną z miar kąta płaskiego jest stopień, który dzieli się na 60 minut i 3600 sekund kątowych).

Stosowany także obecnie system rzymski jest systemem addytywnym. Poznajemy go już w szkole podstawowej, a wykorzystujemy choćby do zapisywania symboli miesięcy lub numerowania wydarzeń odbywających się cyklicznie. W notacji rzymskiej używa się siedmiu symboli:

Jeżeli cyfra o mniejszej wartości stoi przed znakiem o wartości większej, to od liczby większej odejmuje się mniejszą. Gdy z kolei wartość większa poprzedza mniejszą, albo gdy symbole są takie same, dodajemy je do siebie.

System arabski tak naprawdę powstał w Indiach. Jest on najczęściej stosowanym systemem pozycyjnym. Do zapisywania liczb wykorzystuje się w nim cyfry od 0 do 9. W Europie system dziesiętny upowszechnił włoski matematyk Leonardo Fibonacci.

RHzm6kcDKBGQ3

Na rysunku przedstawiono Liczbę 17 w trzech systemach. W systemie egipskim jest ona narysowana jako odwrócone u oraz 7 pionowych kresek. W systemie Majów liczba 17 narysowana jest jako dwie kropki nad stosem trzech poziomych kresek. W systemie babilońskim jako symbol kąta ostrego oraz trzech rzędów trójkątów.

Systemy pozycyjne – zasady zapisywania liczb

W systemie pozycyjnym liczbę zapisujemy jako ciąg cyfr. Każda z nich jest mnożnikiem odpowiadającej jej wagi. Należy pamiętać, że:

• waga jest równa podstawie systemu podniesionej do odpowiedniej potęgi;

• wykładnik potęgi, do której podnosi się podstawę, jest równy pozycji zajmowanej przez cyfrę w liczbie;

• cyfry znajdujące się przed przecinkiem liczymy od strony prawej do lewej (zaczynając od wartości 0 i dla kolejnych cyfr zwiększając ją o 1);

• cyfry znajdujące się po przecinku liczymy od strony lewej do prawej (zaczynając od wartości -1 i zmniejszając ją o 1 dla kolejnych cyfr);

• podstawą systemu może być dowolna liczba (w stosowanym powszechnie systemie dziesiętnym jest nią 10);

• w systemie binarnym podstawą jest liczba 2;

• od podstawy systemu zależy liczba wykorzystywanych w nim symboli;

• w systemie dziesiętnym używa się cyfr 0, 1, 2, 3, 4, 5, 6, 7, 8, 9;

• w systemie binarnym wykorzystuje się cyfry 0 oraz 1;

• w systemie szesnastkowym używane są symbole 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F;

• za pomocą systemu pozycyjnego możemy zapisywać również ułamki (wykładniki potęg, do których podnosi się podstawę systemu, są wówczas ujemne);

• liczby zapisane w systemie innym niż dziesiętny oznaczamy za pomocą dolnego indeksu, którego wartość odpowiada podstawie systemu, przykładowo, jako ciąg 1100101110Indeks dolny (2)₍₂₎;

• wartością liczbywartość liczbywartością liczby o reprezentacji {xIndeks dolny i_i xIndeks dolny i‑1_i‑1 ... xIndeks dolny 1₁ xIndeks dolny 0₀, xIndeks dolny -1_-1xIndeks dolny -2_-2...}Indeks dolny (βbeta) Indeks dolny koniec_(βbeta) jest:

  $$x_i{\beta }^i+x_{i-1}{\beta }^{i-1}+\dots +x_1{\beta }^1+x_0{\beta }^0+x_{-1}{\beta }^{-1}+x_{-2}{\beta }^{-2}\dots$$

Słownik