Przeczytaj
Funkcja
Przypomnijmy definicję funkcji.
Funkcją ze zbioru w zbiór (zbiory i są niepuste) nazywamy takie odwzorowanie, w którym każdemu elementowi ze zbioru został przyporządkowany tylko jeden element ze zbioru .
Funkcję tę oznaczamy .
Zbiór nazywamy dziedziną funkcji i oznaczamy .
Zbiór nazywamy przeciwdziedziną funkcji .
Zbiorem wartości funkcji nazywamy zbiór tych elementów ze zbioru , które zostały przypisane elementom ze zbioru i oznaczamy symbolem .
Do opisu funkcji najczęściej wykorzystujemy:
graf,
opis słowny,
tabelkę,
zbiór par uporządkowanych,
wykres,
wzór.
Prześledźmy powyższe sposoby, analizując przykłady.
Graf

Z grafu można odczytać, że dziedziną funkcji jest zbiór , zaś przaciwdziedziną zbiór . Strzałki pokazują sposób przyporządkowania elementom dziedziny elementów przeciwdziedziny. Zapis czytamy: dla argumentu wartość funkcji jest równa , czyli .
Opis słowny
Funkcję opisujemy pełnym zdaniem, podajemy jej dziedzinę i dokładny opis przyporządkowania. Np.: „Funkcja każdemu uczniowi klasy przyporządkowuje jego numer w dzienniku.”
Znając opis funkcji można podać wartości funkcji przyporządkowane poszczególnym argumentom.
Tabelka
Tabelka zbudowana jest z dwóch wierszy. W górnym wierszu znajdują się argumenty funkcji, czyli elementy dziedziny funkcji. W dolnym wierszu umieszczone są wartości, jakie funkcja przyjmuje dla danych argumentów.
Z tabelki możemy na przykład odczytać, że dla argumentu funkcja przyjmuje wartość , natomiast wartość odpowiada argumentowi .
Zbiór par uporządkowanych
Funkcję można opisać za pomocą zbioru par uporządkowanych postaci , gdzie pierwszy element pary oznacza argument, zaś drugi to wartość funkcji dla danego elementu.
Np.: .
Zapis oznacza, że .
Wykres
Wykres funkcjiWykres funkcji jest to zbiór wszystkich punktów płaszczyzny o współrzędnych , w prostokątnym układzie współrzędnych, gdzie należy do dziedziny tej funkcji, natomiast jest wartością funkcji dla argumentu .

Rysunek przedstawia wykres funkcjiwykres funkcji . Wykres składa się z czterech punktów. Współrzędne tych punktów to: , , , .
Z wykresu możemy odczytać na przykład, że oraz że tylko wtedy, gdy . Wykres funkcji składa się tylko z tylu punktów, ile elementów znajduje się w dziedzinie funkcji.
Wzór funkcji
Są trzy główne sposoby zapisywania wzoru funkcji. Na przykład:
, jeżeli ,
, jeżeli ,
, jeżeli .
Znając wzór funkcji możemy stwierdzić, czy dany punkt należy do wykresu funkcjiwykresu funkcji. Możemy również obliczyć wartość funkcji dla danego argumentu.
Np.: , .
Dane są dwa zbiory oraz . Rozważmy funkcję, które odwzorowuje zbiór w zbiór i opiszmy ją różnymi sposobami.
Rozwiązanie:
Opis słowny – każdej liczbie parzystej ze zbioru przyporządkowujemy liczbę , a każdej liczbie nieparzystej liczbę .
Dziedzina funkcji –
Zbiór wartości –
Graf
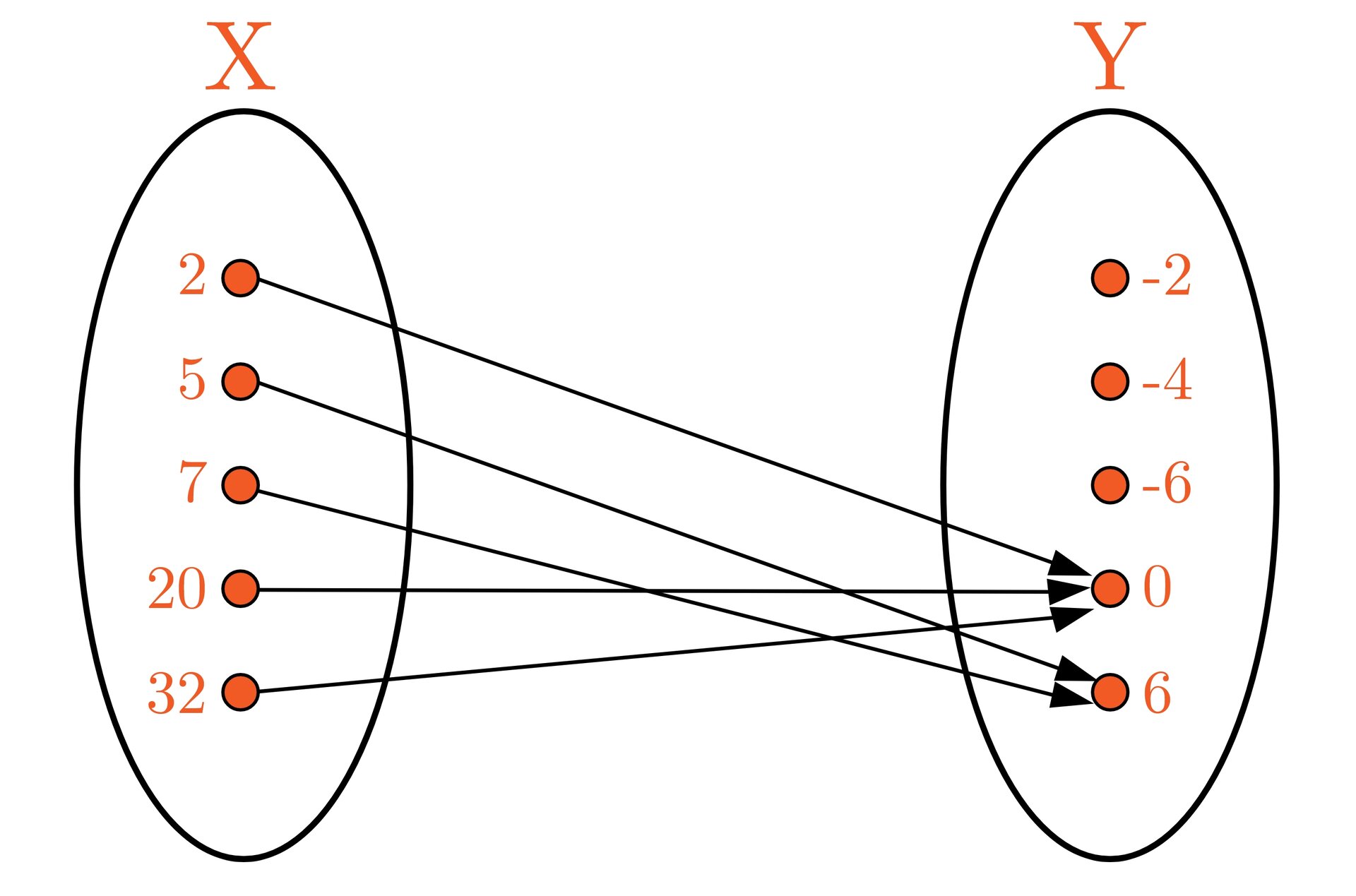
Tabelka
Zbiór par uporządkowanych
.
Wykres

Wzór
Funkcja zapisana jest za pomocą wzoru:
Funkcja każdej liczbie dodatniej przyporządkowuje objętość sześcianu o krawędzi długości . Opiszemy tę funkcję różnymi sposobami.
Rozwiązanie:
Wzór funkcji
Dziedzina funkcji –
Zbiór wartości –
Tabelka
Dziedzina funkcji jest zbiorem nieskończonym. Sporządzamy tabelkę częściową dla pięciu liczb rzeczywistych dodatnich.
Zbiór par uporządkowanych (częściowy)
Wykres (częściowy)

Słownik
wykres funkcji jest to zbiór wszystkich punktów płaszczyzny o współrzędnych , w prostokątnym układzie współrzędnych, gdzie należy do dziedziny tej funkcji, natomiast jest wartością funkcji dla argumentu