Czym jest szyfr RSA?

Nazwa szyfru RSA to skrót od nazwisk trzech profesorów z Massachusetts Institute of Technology w USA, którzy w 1977 r. opublikowali ten algorytm. Byli to Ronald L. Rivest, Adi Shamir i Leonard Adleman.

Szyfr RSA to asymetryczny algorytm kryptograficzny. Posiada parę kluczy – publiczny (e, n) oraz prywatny (d, n).
Postępowanie z użyciem asymetrycznego szyfrowania można sprowadzić do następujących kroków:

• Każda osoba, która chce otrzymać zaszyfrowaną wiadomość, „wystawia” na publiczny widok swój klucz publiczny.

• Osoba chcąca wysłać wiadomość szyfruje ją wykorzystując klucz publiczny osoby, do której chce ją wysłać.

• Osoba, która odbiera wiadomość, odszyfrowuje ją z użyciem swojego klucza prywatnego. Nikt, kto nie posiada klucza prywatnego, nie jest w stanie odszyfrować wiadomości.

Jak wyznaczyć klucz prywatny i publiczny?

1. Wybieramy dwie dowolne liczby pierwsze i oznaczamy je jako p i q. Liczby te powinny być możliwie jak największe.

2. Obliczamy wartość n = p • q. Wartość n jest elementem klucza publicznego i prywatnego, określa również największą możliwą wielkość liczbową wysyłanej przez nas wiadomości.

3. Wyliczamy wartość funkcji Eulera dla n i wybieramy dowolną liczbę e spełniającą warunek (1 < e < φphi(n)), która będzie względnie pierwsza do wartości φphi(n).
   Liczba e jest elementem klucza publicznego.

4. Obliczamy odwrotność modulo φphi(n) liczby e i otrzymujemy liczbę d, która jest elementem klucza prywatnego.

Po zrealizowaniu wszystkich czterech kroków możemy szyfrować i deszyfrować wiadomości zgodnie z następującymi funkcjami:

oraz:

– gdzie $W$ to wiadomość w postaci liczbowej, będąca mniejsza od $n$, a $S$ to szyfrogram wiadomości, którą chcemy odszyfrować.

Dlaczego p i q muszą być liczbami pierwszymi?

Bezpieczeństwo szyfrowania RSA opiera się na trudności faktoryzacji liczbfaktoryzacja liczbfaktoryzacji liczb. Faktoryzacja liczby będącej iloczynem liczb pierwszychliczba pierwszaliczb pierwszych, jest bardziej złożona niż faktoryzacja liczb będących iloczynem liczb złożonych. Stąd też p i q muszą być pierwsze.

Drugim powodem tego stanu rzeczy, jest to, że dla liczb pierwszych funkcja Eulera przyjmie następującą postać:

Korzystamy tu z następującej właściwości funkcji Eulera:

Jeśli x jest liczbą pierwszą to:

– gdzie p i q to liczby pierwsze o wykładniku równym 1.
Gdyby p i q nie byłyby liczbami pierwszymi, to funkcja Eulera przyjęłaby dużo bardziej złożoną postać, przez co obliczenie jej stałoby się obiektywnie trudniejsze, co w praktycznych zastosowaniach byłoby niekorzystne. Jest to jednak powód drugorzędny.

Załóżmy, że chcemy poznać czyjś klucz prywatny. Klucz publiczny tej osoby jest znany i przyjmuje np. takie wartości: e = 3 i n = 33. Z racji tego, że n jest niewielkie, możemy bez większego problemu – przy użyciu tzw. metody brutalnej (siłowej) – ustalić, że p = 11 i q = 3. Tutaj należy zwrócić uwagę, że nie istnieje inna niż 11 i 3 kombinacja liczb, która po pomnożeniu dałaby wynik 33.

Przyjmijmy, że n = 2501. Istnieje tylko jedna kombinacja liczb, których iloczyn wynosi dokładnie tyle, ponieważ zmienne p i q są liczbami pierwszymi. Próba odnalezienia czynników pierwszych metodą brutalną w przypadku n = 2501 jest już bardziej złożona obliczeniowo. Korzystając z niej, musielibyśmy wykonać 40 razy operację dzielenia, zanim odnaleźlibyśmy pierwszy czynnik pierwszy, czyli w tym przypadku p równego 41. W tym przykładzie q jest równe 61.

Dla porównania załóżmy teraz, że n = 6840. Liczbę 6840 możemy otrzymać poprzez pomnożenie np. 3420 przez 2, 1710 przez 4, czy też 684 przez 10. Istnieje wiele kombinacji liczb złożonych, dzięki której otrzymalibyśmy wartość takiego n.
Reasumując: jeśli p i q nie są pierwsze, to jesteśmy w stanie rozbić liczbę n na wiele czynników pierwszych. Wtedy, pomimo tego, że obliczenie funkcji Eulera staje się potencjalnie dużo bardziej złożone obliczeniowo, to odnalezienie wszystkich czynników pierwszych jest prostsze, a bezpieczeństwo samego szyfrowania opiera się właśnie na trudności rozkładu liczby n na czynniki pierwsze. Gdy p i q nie są pierwsze, to możemy skorzystać z innego wzoru na obliczanie funkcji Eulera, a mianowicie:

- gdzie pIndeks dolny 11, pIndeks dolny 22, ..., pIndeks dolny kk są czynnikami pierwszymi bez powtórzeń.
Przykładowo, dla liczby 32 jedynym czynnikiem pierwszym byłoby 2, podobnie jak dla liczby 1024 lub 8192. Wtedy:

Jeżeli próbowalibyśmy metodą brutalną odnaleźć wszystkie czynniki pierwsze liczby 8192, to odnaleźlibyśmy je bardzo szybko, ponieważ mimo tego, że liczba ta jest większa niż 2501, dużo prościej się rozkłada.

W przypadku liczb będących iloczynem liczb złożonych jesteśmy w stanie dużo szybciej znaleźć wszystkie czynniki pierwsze metodą brutalną. Aby odnaleźć czynnik pierwszy liczby będącej iloczynem dwóch liczb pierwszych metodą brutalną, musimy w praktyce przeszukać dużo więcej liczb, ponieważ w jej przypadku są tylko dwa czynniki pierwsze.

Jeśli wejdziemy w posiadanie czynników pierwszych, będziemy mogli obliczyć funkcję Eulera, a następnie na tej podstawie będziemy w stanie obliczyć odwrotność modulo e liczby φphi(n). Wtedy też nasz klucz zostałby złamany.

Aby obliczyć odwrotność modulo, również należy posługiwać się liczbami pierwszymi.

Odwrotność modulo

Obliczenie odwrotności modulo można przeprowadzić na wiele sposobów, ale żaden z nich nie ma złożoności wielomianowej. Najprostszą metodą jest metoda naiwna polegająca na podstawianiu pod x kolejnych wartości, dopóki nie uzyska się poprawnego wyniku.

Dobrym wyborem jest skorzystanie z rozszerzonego algorytmu Euklidesa.

Załóżmy, że chcemy obliczyć odwrotność modulo 5 liczby 2. W tym celu musimy więc rozwiązać następujące działanie:

Następnie należy odnaleźć x.

Przeprowadzimy to przy użyciu metody brutalnej:
2 ∙ 1, czyli 2 modulo 5 = 2
2 ∙ 2, czyli 4  modulo 5 = 4
2 ∙ 3, czyli 6 modulo 5 = 1

Zatem pod x możemy wstawić 3.

Nie jest to jednak jedyne rozwiązanie – próbując dalej, będziemy odnajdywać kolejne możliwe wartości x:
2 ∙ 4, czyli 8 modulo 5 = 3
2 ∙ 5, czyli 10 modulo 5 = 0
2 ∙ 6, czyli 12 modulo 5 = 2
2 ∙ 7, czyli 14 modulo 5 = 4
2 ∙ 8, czyli 16 modulo 5 = 1

Zatem pod x można również podstawić 8.

Czy wybór składnika d w kluczu prywatnym ma znaczenie?

Udowodniliśmy, że modulo 5 liczby 2 ma co najmniej dwa rozwiązania – prawda jest jednak taka, że rozwiązań tych jest nieskończenie wiele. Czy istnieje jednak najlepszy wybór wyniku dla klucza prywatnego?

Zaprezentowane wyżej szyfrowanie ma następującą postać:

a z kolei deszyfrowanie będzie miało taką postać:

Na zaprezentowanym powyżej przykładzie widać, że dla poprawności algorytmu nie ma znaczenia, jaką liczbę wybierzemy jako d, dopóki będzie ona odwrotnością modulo φphi(n) liczby e. Z obliczeniowego punktu widzenia najkorzystniejszą decyzją jest wybranie mniejszego d, jednakże d nie powinno być równe e. Należy unikać sytuacji, w których klucz prywatny i klucz publiczny posiada takie same wartości, ponieważ byłaby to słabość, która mogłaby zostać wykorzystana przez naszego potencjalnego przeciwnika. W tym przypadku najlepszym wyborem, ze względu na bezpieczeństwo, byłoby więc wybranie d równego 11.

Dlaczego szyfrowanie i deszyfrowanie działa?

Poniższa funkcja:

oraz funkcja odwrotna:

służą kolejno do szyfrowania i deszyfrowania, a zasada ich działania opiera się na arytmetyce modularnej, którą można wyjaśnić na przykładzie zegara.

RSuZwsnNvl2rd

Grafika przedstawiająca tarczę zegara. Na zegarze zaznaczono godziny: 12, 3, 6 oraz 9. Zegar wskazuje godzinę 3.

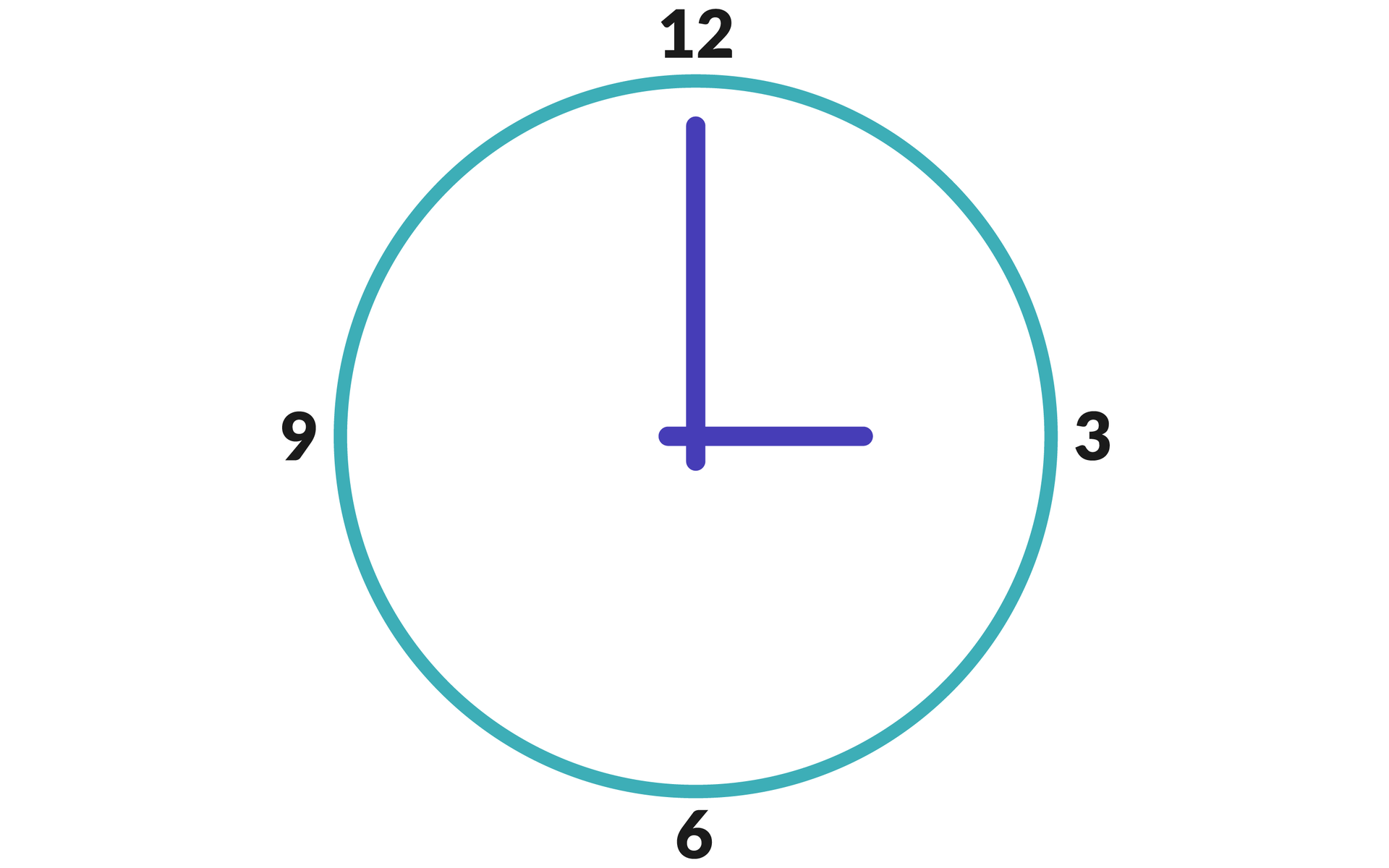
Zegar wskazuje godzinę trzecią – dla przykładu załóżmy, że interesuje nas jedynie zachowanie wskazówki godzinowej. Mija 12 godzin – zegar ponownie wskazuje godzinę trzecią. Czy czas stanął w miejscu? Czy jest to ta sama godzina trzecia, co 12 godzin temu? Oczywiście, że nie.

Stwierdzenie więc, że 3 + 12 = 3 jest niepoprawne, ponieważ godziny te nie są sobie równe, lecz są do siebie przystające. W matematyce operację przystawania zapisujemy tak:

Możemy też zapisać tę relację w nastepujący sposób:

Przedstawiona wcześniej reguła z zegarem matematycznie prezentowałaby się więc tak:

Operacja szyfrowania i deszyfrowania opiera się na następującej zasadzie:

Dlatego też wysyłana przez nas wiadomość w postaci liczbowej musi być mniejsza od n, ponieważ wtedy nawet dla e = 1 i d = 1 wiadomość, którą chcemy wysłać, byłaby różna od tej, którą finalnie otrzymamy.

Teoria a praktyka

Im większe liczby pierwsze p i q, tym trudniej jest odgadnąć choćby jedną z nich. Można tu sobie zadać zasadne pytanie: skoro atakujący wie, że korzystamy jedynie z liczb pierwszych, to czemu nie odnajdzie wszystkich liczb pierwszych i nie sprawdzi po prostu wszystkich kombinacji?

Głównym problemem takiej strategii jest fakt, że liczb pierwszych jest nieskończenie wiele, zatem chcąc przeciwdziałać metodzie brutalnej, powinniśmy za nasze p i q przyjąć możliwie jak największe liczby pierwsze, które są podobnych rzędów wielkości. Właśnie dlatego w praktycznych zastosowaniach używa się kluczy mających po kilkaset bitów (dla przypomnienia: liczba mająca 64 bity może mieć maksymalnie wartość 18 446 744 073 709 551 615).

Jak już powiedzieliśmy, liczb pierwszych jest nieskończenie wiele. Największą znaną i potwierdzoną liczbą pierwszą na dzień 21.06.2020 jest liczba składająca się z 22 338 618 cyfr.

Wzór na oszacowanie liczby liczb pierwszych pomiędzy 0 a x to:

Błąd dla x = 50000 wynosi jedynie 0,6% i dla większych wartości tylko się zmniejsza.
Czyli liczb pierwszych do liczby 50000 jest około 4621 +/- 0,6%.

Słownik