Przeczytaj
Funkcję określoną na zbiorze wzorem
gdzie , nazywamy funkcją liniową.
Liczbę nazywamy współczynnikiem kierunkowym, a wyrazem wolnym.
Wykresem funkcji liniowej jest prosta.
Wartości współczynników i w zależności od położenia prostej, będącej wykresem funkcji liniowej określonej wzorem w prostokątnym układzie współrzędnych
-
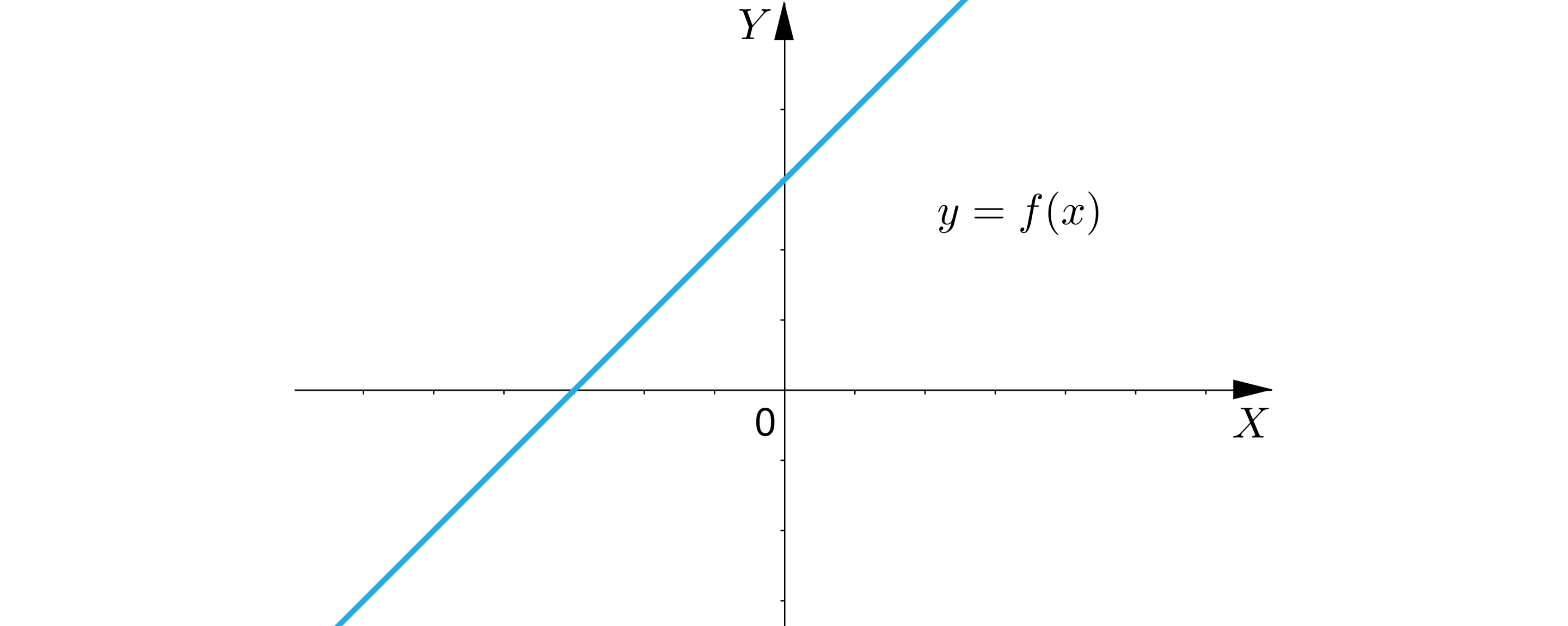
i Wykres funkcji znajduje się w , i ćwiartce układu współrzędnych.
-
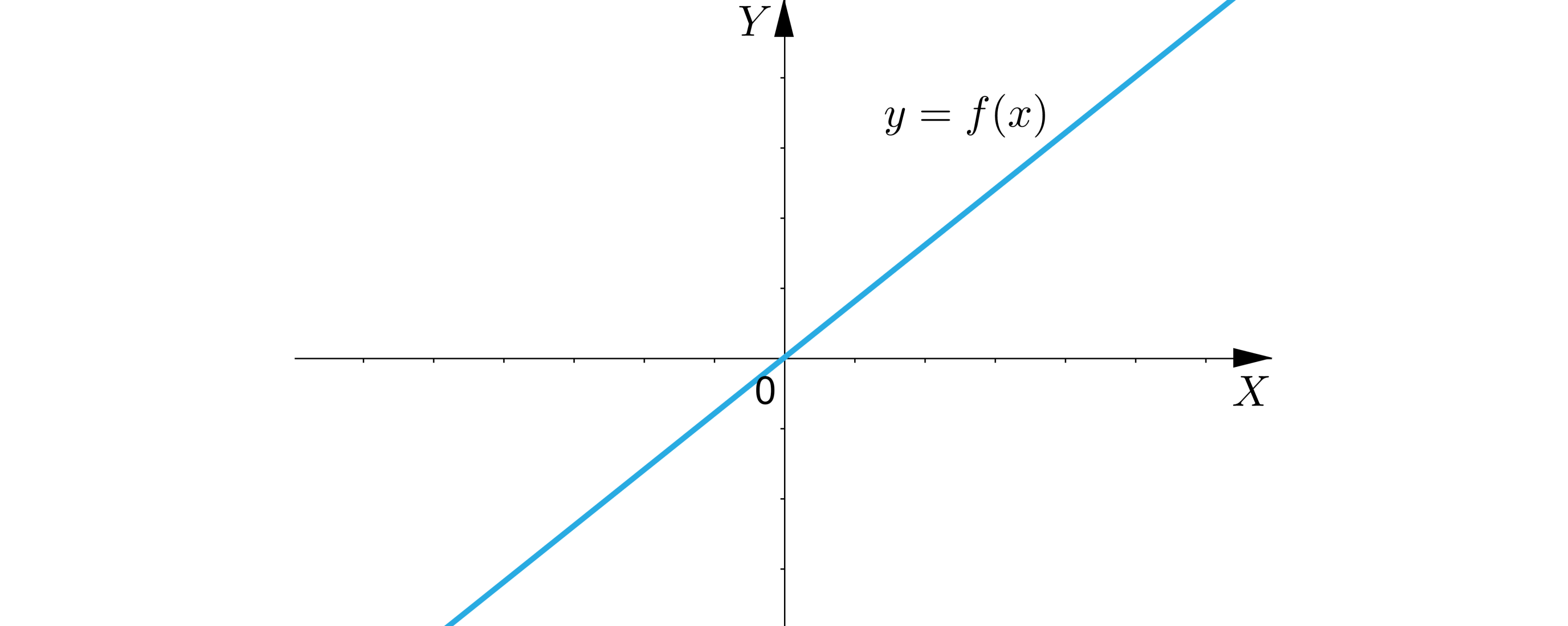
i Wykres funkcji znajduje się w i ćwiartce układu współrzędnych, przechodzi przez początek układu współrzędnych.
-
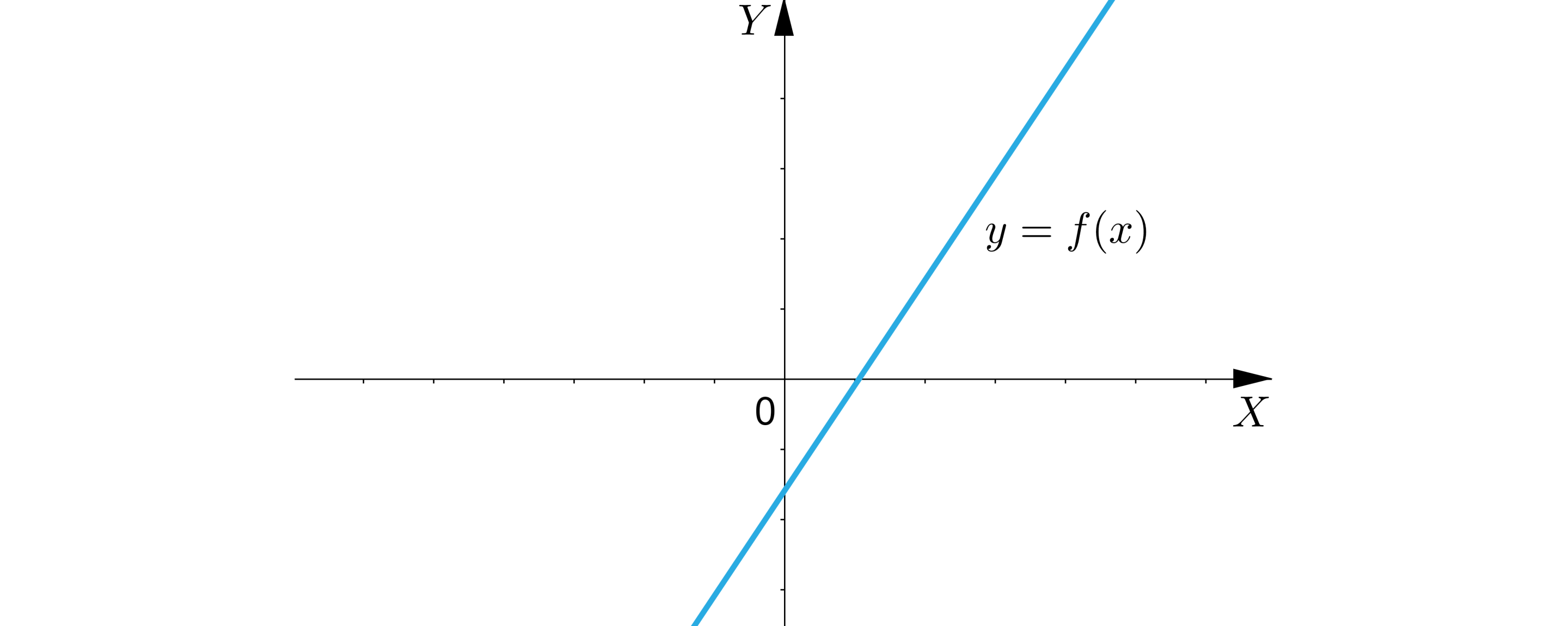
i Wykres funkcji znajduje się w , i ćwiartce układu współrzędnych.
-

i Wykres funkcji znajduje się w , i ćwiartce układu współrzędnych.
-
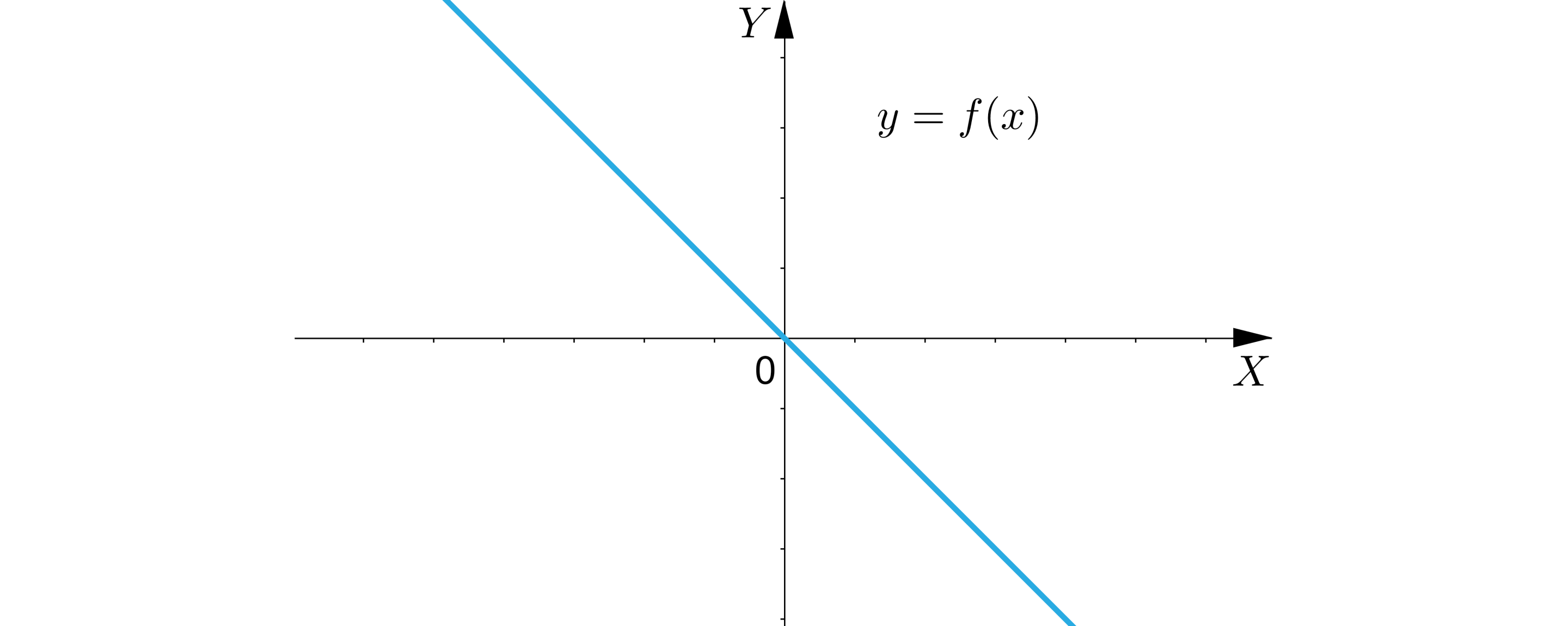
i Wykres funkcji znajduje się w i ćwiartce układu współrzędnych, przechodzi przez początek układu współrzędnych.
-

i Wykres funkcji znajduje się w , i ćwiartce układu współrzędnych.
-
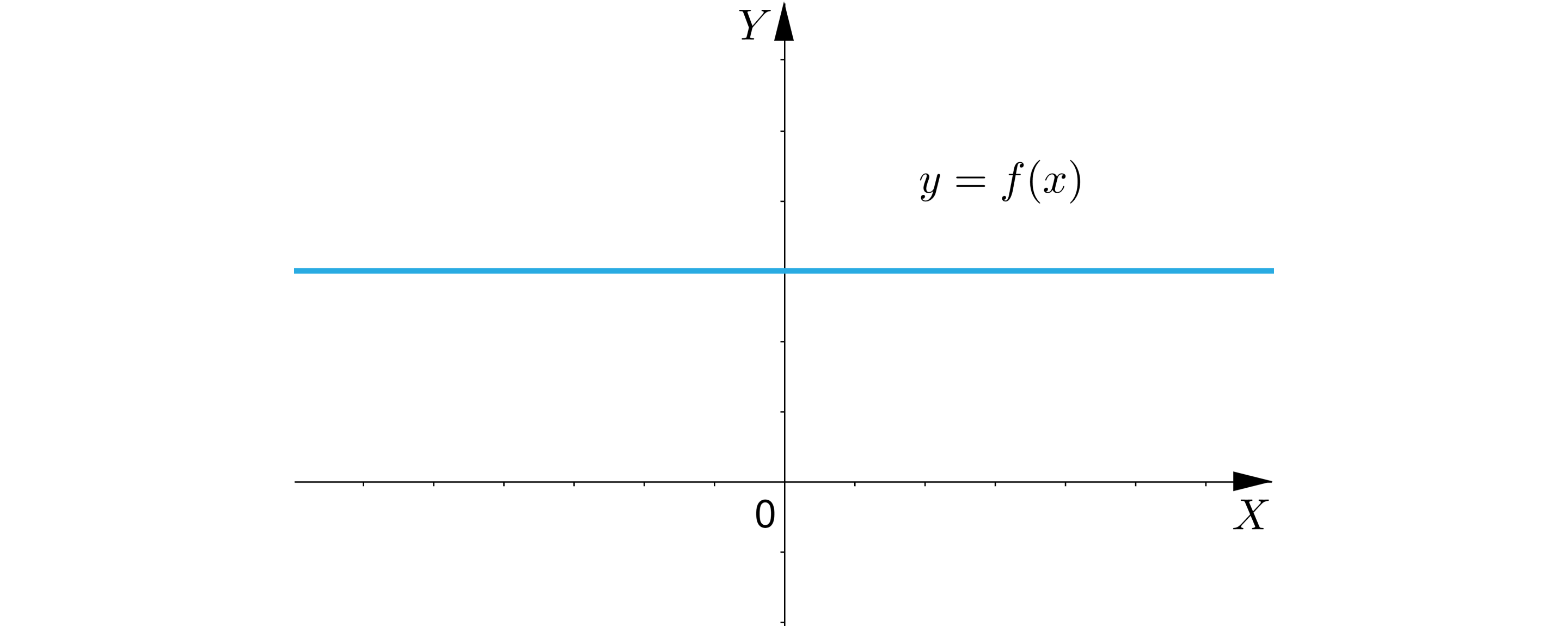
i Wykres funkcji znajduje się w i ćwiartce układu współrzędnych, jest równoległy do osi .
-
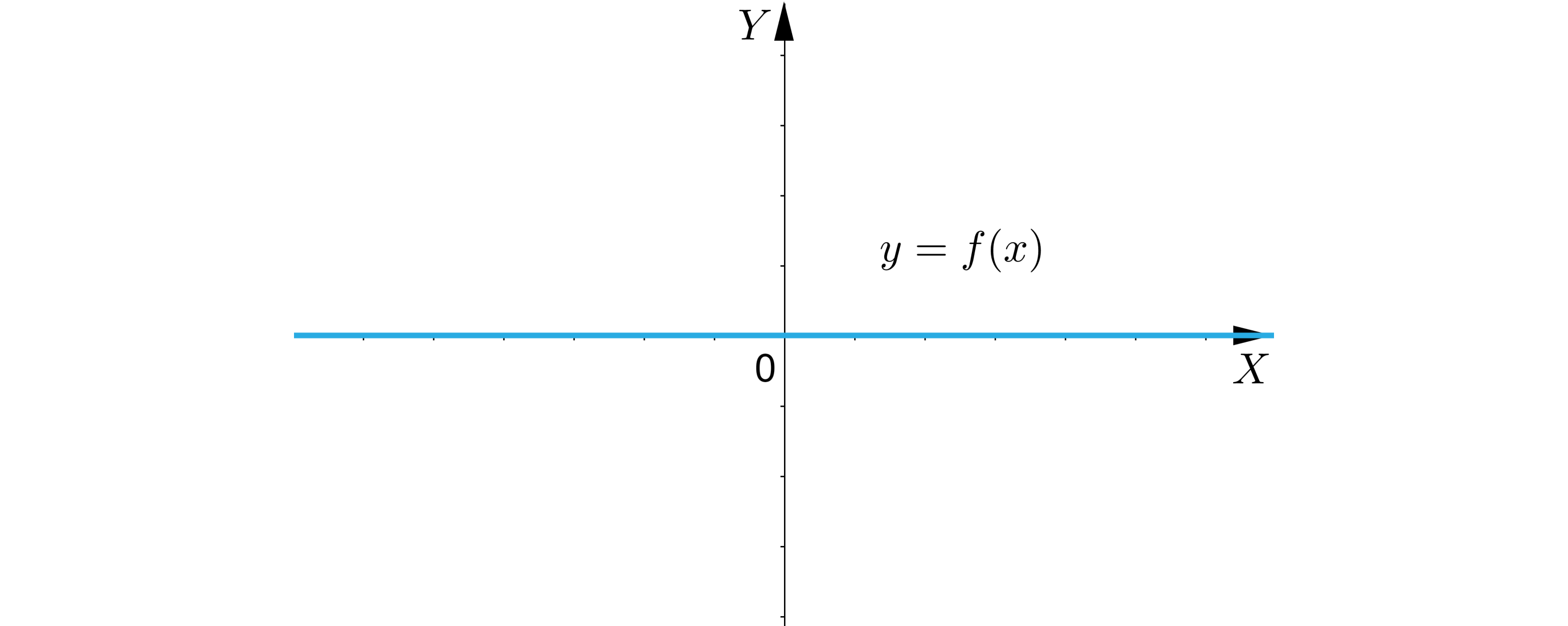
i Wykres funkcji jest zawarty w osi .
-
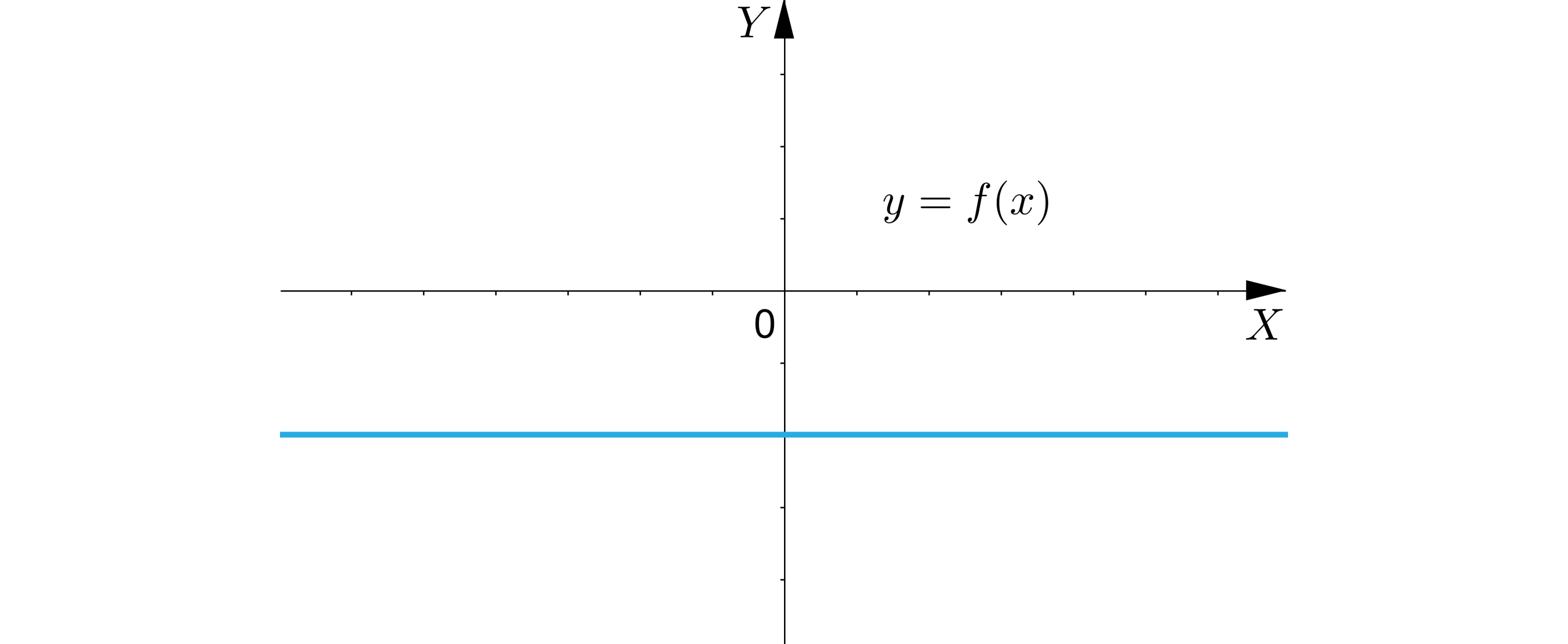
i Wykres funkcji znajduje się w i ćwiartce układu współrzędnych, jest równoległy do osi .
Wartości współczynników a i b w zależności od położenia prostej, będącej wykresem funkcji liniowej określonej wzorem f(x)=ax+b w prostokątnym układzie współrzędnych.
Slajd pierwszy.
Ilustracja przedstawia układ współrzędnych z poziomą osią X oraz pionową osią Y. Zaznaczono na nim prostą rosnącą.
a większe od zera i b większe od zera. Wykres funkcji znajduje się w pierwszej drugiej i trzeciej ćwiartce układu współrzędnych.
Slajd drugi
Ilustracja przedstawia układ współrzędnych z poziomą osią X oraz pionową osią Y. Zaznaczono na nim prostą rosnącą.
a większe od zera i b równe zero.
Wykres funkcji znajduje się w pierwszej i drugiej ćwiartce układu współrzędnych, przechodzi przez początek układu współrzędnych.
Slajd trzeci.
Ilustracja przedstawia układ współrzędnych z poziomą osią X oraz pionową osią Y. Zaznaczono na nim prostą rosnącą.
a większe od zera i b mniejsze od zera.
Wykres funkcji znajduje się w pierwszej, trzeciej i czwartej ćwiartce układu współrzędnych.
Slajd czwarty.
Ilustracja przedstawia układ współrzędnych z poziomą osią X oraz pionową osią Y. Zaznaczono na nim prostą malejącą.
a mniejsze od zera i b większe od zera.
Wykres funkcji znajduje się w pierwszej, drugiej i czwartej ćwiartce układu współrzędnych.
Slajd piąty.
Ilustracja przedstawia układ współrzędnych z poziomą osią X oraz pionową osią Y. Zaznaczono na nim prostą malejącą.
a mniejsze od zera i b równe zero.
Wykres funkcji znajduje się w drugiej i czwartej ćwiartce układu współrzędnych , przechodzi przez początek układu współrzędnych.
Slajd szósty.
Ilustracja przedstawia układ współrzędnych z poziomą osią X oraz pionową osią Y. Zaznaczono na nim prostą malejącą.
a mniejsze od zera i b mniejsze od zera.
Wykres funkcji znajduje się w drugiej, trzeciej i czwartej ćwiartce układu współrzędnych.
Slajd siódmy.
Ilustracja przedstawia układ współrzędnych z poziomą osią X oraz pionową osią Y. Zaznaczono na nim prostą.
a równe zero i b większe od zera.
Wykres funkcji znajduję się w pierwszej i drugiej ćwiartce układu współrzędnych, jest równoległy do osi X.
Slajd ósmy.
Ilustracja przedstawia układ współrzędnych z poziomą osią X oraz pionową osią Y. Zaznaczono na nim prostą malejącą.
a równe zero i b równe zero.
Wykres funkcji jest zawarty w osi X.
Slajd dziewiąty.
Ilustracja przedstawia układ współrzędnych z poziomą osią X oraz pionową osią Y. Zaznaczono na nim prostą malejącą.
a równe zero i b mniejsze od zera.
Wykres funkcji znajduję się w trzeciej i czwartej ćwiartce układu współrzędnych, jest równoległy do osi X.
Znajdowanie wartości współczynników liczbowych i
Jeżeli dana jest prosta, będąca wykresem funkcji liniowejfunkcji liniowej w prostokątnym układzie współrzędnych, to:
wartość współczynnika obliczamy ze wzoru:
,gdzie:
oraz są współrzędnymi dowolnych dwóch punktów, które należą do prostej, będącej wykresem funkcji liniowej,
wartość współczynnika jest równa drugiej współrzędnej punktu przecięcia prostej, będącej wykresem funkcji liniowej z osią .
Jeżeli funkcja liniowa jest określona wzorem , to do prostej, będącej wykresem tej funkcji należy punkt o współrzędnych .
Określimy wartości współczynników liczbowych funkcji liniowej określonej wzorem , jeżeli wiadomo, że do prostej, będącej wykresem tej funkcji należą punkty o współrzędnych oraz .
Rozwiązanie:
Jeżeli punkt o współrzędnych należy do prostej, będącej wykresem tej funkcji, to .
Obliczamy wartość współczynnika , korzystając ze wzoru.
Zatem:
.
Wyznaczymy, dla jakich wartości parametru prosta, będąca wykresem funkcji liniowej określonej wzorem należy do , i ćwiartki układu współrzędnych.
Rozwiązanie:
Wartości współczynników i ze wzoru funkcji wynoszą odpowiednio:
,
.
Jeżeli prosta, będąca wykresem funkcji liniowej określonej wzorem należy do , i ćwiartki układu współrzędnych, to zachodzą następujące warunki:
i .
Zatem do wyznaczenia wartości parametru rozwiązujemy nierówności:
, więc , zatem ,
, więc , zatem .
Wobec tego oba warunki są spełnione, gdy .
Wyznaczymy, dla jakich wartości parametru wykresem funkcji liniowej określonej wzorem jest prosta, która jest równoległa do osi układu współrzędnych.
Rozwiązanie:
Jeżeli prosta, będąca wykresem funkcji liniowej określonej wzorem jest równoległa do osi , to i .
Zatem do wyznaczenia wartości parametru rozwiązujemy równanie, wykorzystując metodę grupowania wyrazów:
, czyli ,
, czyli .
Wobec tego .
Sprawdzenie:
Zatem funkcja liniowa jest określona wzorem:
Ponieważ i , to prosta, będąca wykresem funkcji jest równoległa do osi układu współrzędnych.
Sprawdzimy, czy prosta, będąca wykresem funkcji liniowej określonej wzorem należy do , i ćwiartki układu współrzędnych, jeżeli do wykresu tej funkcji należy punkt o współrzędnych .
Rozwiązanie:
Jeżeli do prostej, będącej wykresem funkcji należy punkt o współrzędnych , to do wyznaczenia wartości parametru rozwiązujemy równanie:
.
Dla mamy:
.
Ponieważ i , to prosta, będąca wykresem tej funkcji znajduje się w , i ćwiartce układu współrzędnych.
Dla mamy:
Ponieważ oraz , to prosta, będąca wykresem tej funkcji znajduje się w , i ćwiartce układu współrzędnych.
Określimy wartości współczynników liczbowych i we wzorze funkcji liniowej określonej wzorem jeżeli wiadomo, że prosta, będąca wykresem tej funkcji przechodzi przez punkt o współrzędnych i wraz z osiami układu współrzędnych ogranicza trójkąt o polu równym .
Rozwiązanie:
Wykonajmy rysunek pomocniczy do zadania. Zauważmy, że istnieją takie dwie proste, będące wykresami funkcji liniowych, które spełniają warunki określone w zadaniu.
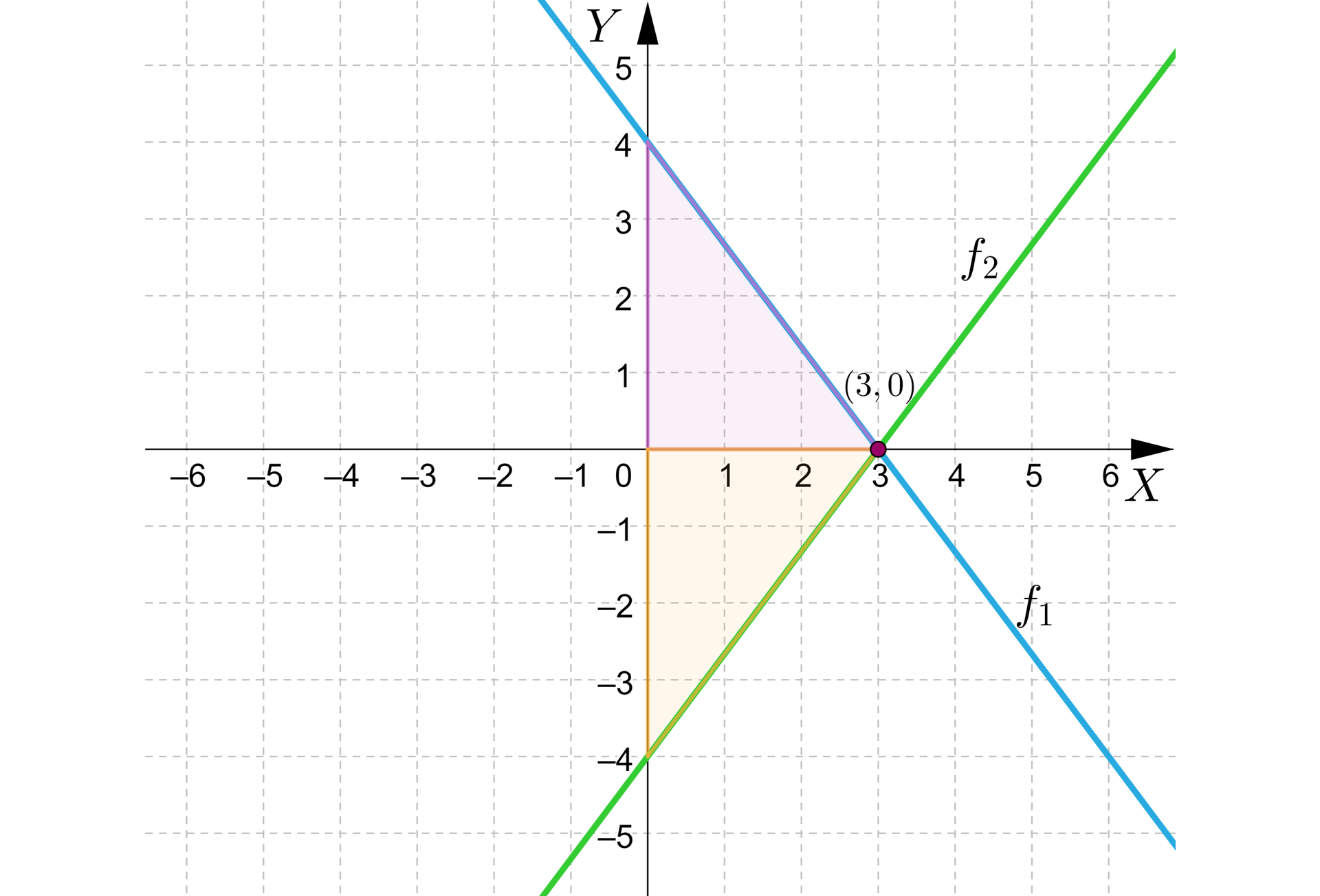
Ponieważ pole trójkąta ograniczonego przez prostą, będącą wykresem funkcji liniowej oraz osie układu współrzędnych wynosi , to do wyznaczenia wartości rozwiązujemy równanie:
Zauważmy, że wartość współczynnika we wzorze funkcji liniowej może też wynosić .
Zatem funkcja liniowa, której wykres ogranicza wraz z osiami układu współrzędnych podany trójkąt jest określona za pomocą wzoru:
lub
Ponieważ punkt o współrzędnych należy do prostej, będącej wykresem funkcji , zatem:
, wtedy , czyli
, wtedy , czyli
Uzasadnimy, że jeśli i , to równanie prostej , będącej wykresem funkcji liniowej można zapisać w postaci .
Rozwiązanie:
Dana jest prosta o równaniu , będąca wykresem funkcji liniowej.
Przekształcamy równanie tej prostej do postaci:
Po podzieleniu obu stron równania przez otrzymujemy:
Równanie zapisujemy w szukanej postaci:
Słownik
funkcja określona na zbiorze wzorem , gdzie ,