Przeczytaj

Siatką bryły nazywamy takie przedstawienie bryły na płaszczyźnie, aby po wycięciu można było tę bryłę skleić budując jej model.

Siatka walcawalecwalca składa się z prostokąta będącego powierzchnią boczną (jeden z boków prostokąta jest wysokością walcawysokość walcawysokością walca, a długość drugiego jest równa obwodowi koła będącego podstawą walca) oraz dwóch kół będących podstawami walca (stycznymi do przeciwległych boków prostokąta długości równej obwodowi podstawy).

RgRGW8cd0eP13

Ilustracja przedstawia walec oraz jego siatkę. Walec posiada promień o długości r oraz wysokość o długości h. Jego siatka składa się z prostokąta o wymiarach dwa pi r na h oraz z dwóch kół o promieniu r stycznych do dwóch dłuższych przeciwległych boków prostokąta.

Przykład 1

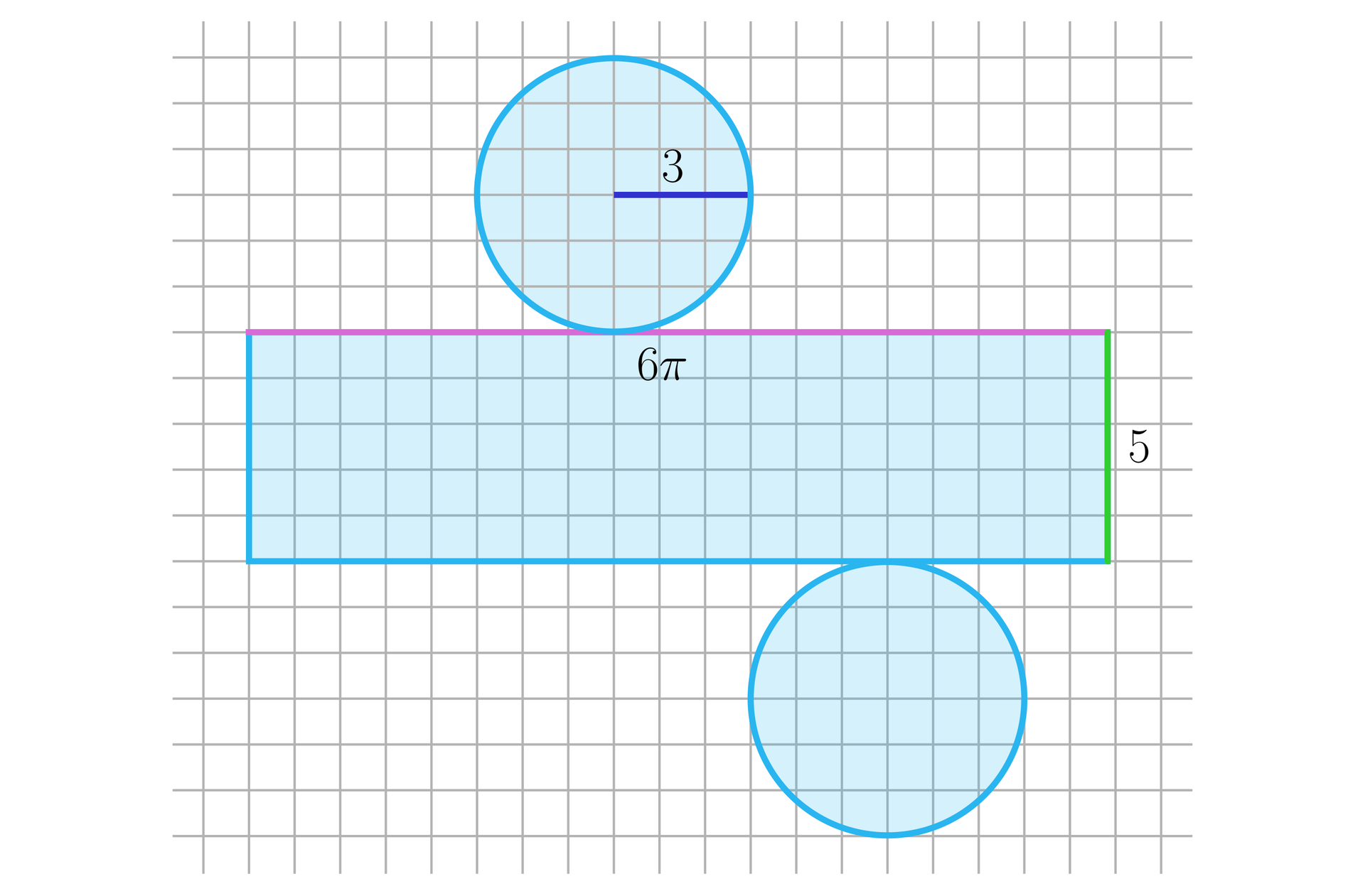
Narysujemy siatkę walca o promieniu podstawy $3$ i wysokości $5$ .

Rozwiązanie

Przyjmujemy jedną kratkę jako jedną jednostkę. Powierzchnia boczna będzie więc prostokątem o wymiarach $6 π \times 5$ . Czyli około $18, 86 \times 5$ . Narysujmy tę siatkę:

R1dJcfmc8NEGv

Ilustracja przedstawia siatkę walca składającą się z prostokąta o wymiarach sześć pi na pięć oraz dwóch kół o promieniu równym 5 stycznych do dwóch dłuższych przeciwległych boków prostokąta.

Przykład 2

Ustalimy, czy na kartce papieru w rozmiarze A4 możemy narysować siatkę walca o promieniu podstawy $4, 5 cm$ i wysokości $5 cm$ tak, aby aby boki powierzchni bocznej były równoległe do krawędzi kartki. Sprawdzimy, czy narysujemy siatkę tego walca na kartce w rozmiarze B4.

Rozwiązanie

Długość prostokąta będącego powierzchnią boczną wynosi $9 π \approx 28, 3 cm$ , a zatem możemy go narysować wzdłuż dłuższej krawędzi kartki A4, która ma $297 mm$ .

Druga krawędź kartki ma długość $210 mm$ , a my potrzebujemy $4 r + h = 18 + 5 = 23 cm$ .

A zatem na kartce A4 nie wykonamy takiej siatki.

Kartka B4 ma wymiary $250 m m \times 353 m m$ . Tak więc siatka ta zmieści się na kartce B4.

Uwaga!

Aby narysować siatkę walca powinniśmy znać wysokość walca i promień podstawy. Czasem informacje te nie są wprost podane w treści zadania, ale można je policzyć.

Przykład 3

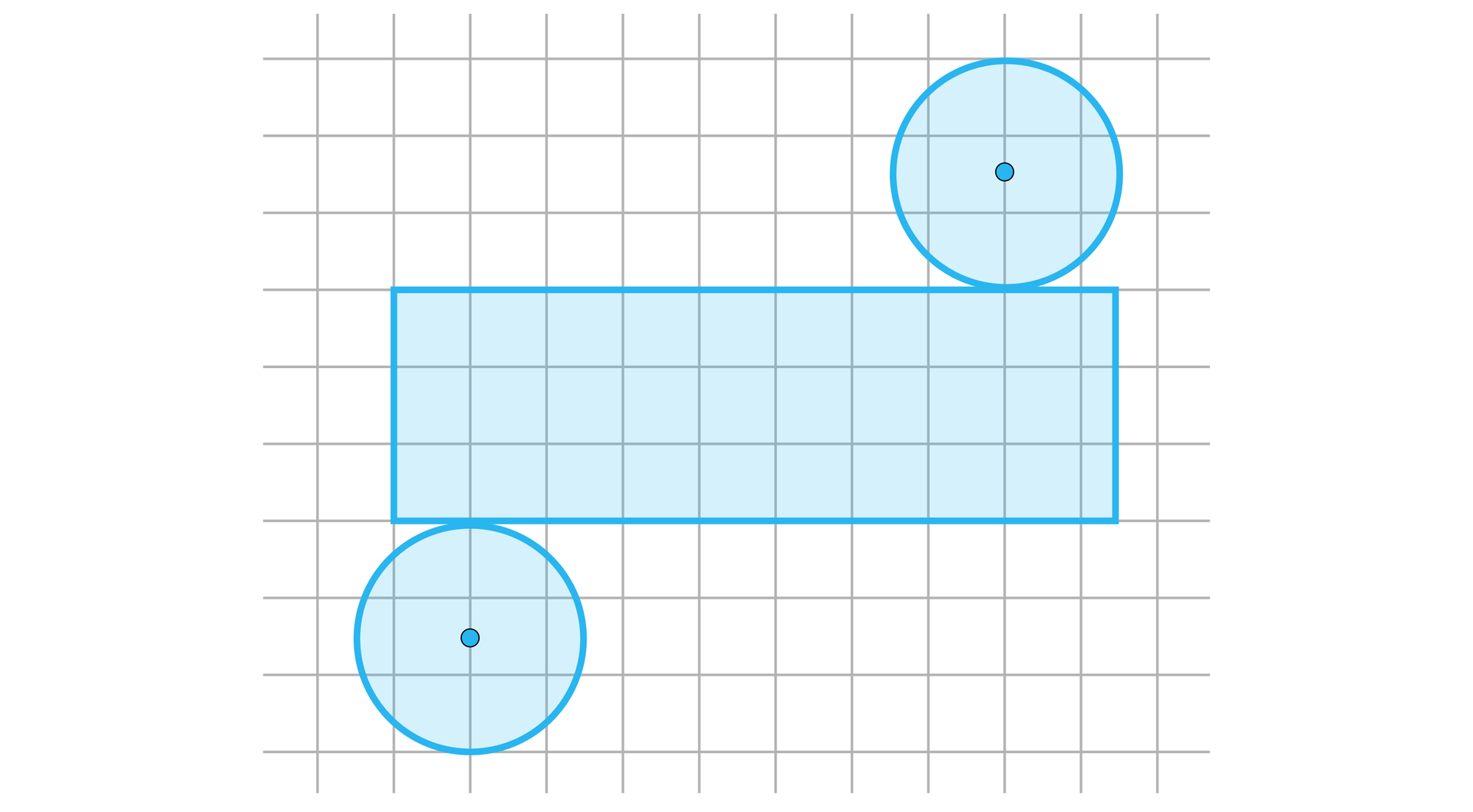
Wysokość walca jest dwukrotnie dłuższa od promienia jego podstawy. Pole podstawy walca wynosi $2, 25 π$ . Narysujemy siatkę tego walca.

Rozwiązanie

Najpierw obliczymy promień podstawy tego walca. Mamy, że $π r^{2} = 2, 25 π$ . A zatem $r^{2} = 2, 25$ , co daje $r = 1, 5$ . Mamy więc $h = 3$ .

Długość tego okręgu wynosi $2 \cdot 1, 5 π = 3 π \approx 9, 42$ .

Narysujmy siatkę tego walca:

RsUsOvpZjYtNc

Ilustracja przedstawia siatkę walca składającą się z prostokąta oraz dwóch kół stycznych do dwóch dłuższych przeciwległych boków prostokąta.

Przykład 4

Pole powierzchni bocznej walca wynosi $24 π$ , a wysokość walca jest o $4$ dłuższa od promienia podstawy. Narysujemy siatkę tego walca.

Rozwiązanie

Pole powierzchni bocznej to pole prostokąta o wymiarach $h \times 2 π r$ , przy czym $h = r + 4$ .

Mamy więc $2 π r (r + 4) = 24 π$ . Czyli $r^{2} + 4 r = 12$ .

Rozwiążemy równanie kwadratowe $r^{2} + 4 r - 12 = 0$ .

Mamy, że $∆ = 64$ i stąd $r_{1} = 2$ lub $r_{2} = - 6 < 0$ . A zatem $r = 2$ i $h = 6$ .

Narysujmy siatkę tego walca:

Ri0mU6plGTVcp

Mając siatkę walca możemy obliczyć długości odcinków i inne wielkości związane z walcami.

Przykład 5

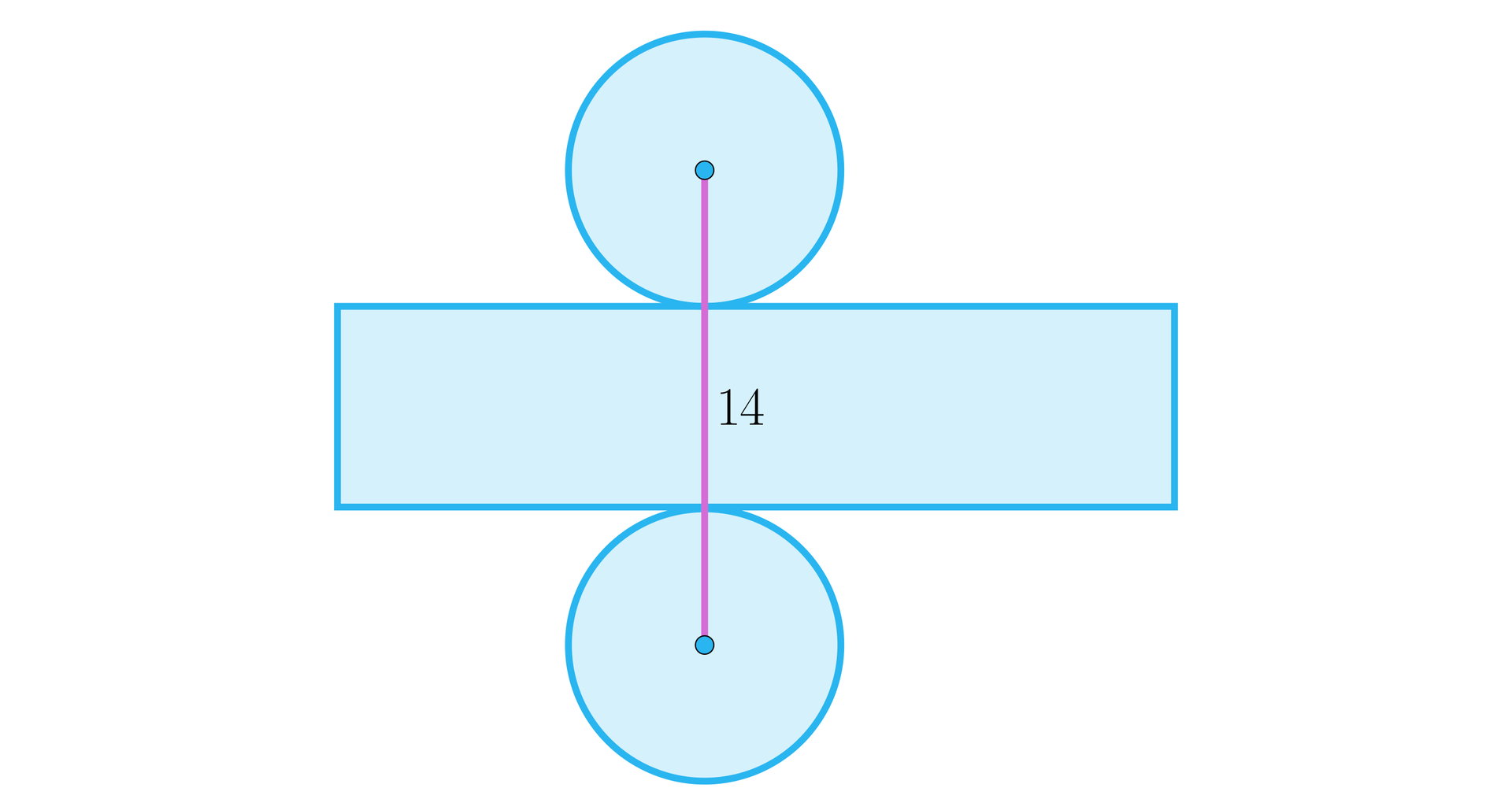
Dana jest siatka walca jak na rysunku poniżej. Obliczymy pole powierzchni bocznej tego walca, wiedząc, że stosunek promienia podstawy do wysokości wynosi $2 : 3$ , a odcinek łączący środki okręgów jest równoległy do wysokości.

RXddFsnUfXW7j

Rozwiązanie

Odcinek zaznaczony na rysunku ma długość $2 r + h$ . Stosunek promienia do wysokości wynosi $2 : 3$ , czyli $r = 2 x$ i $h = 3 x$ , dla pewnego współczynnika $x$ .

Mamy więc $4 x + 3 x = 14$ , a stąd $x = 2$ . A zatem $r = 4$ i $h = 6$ . Teraz już możemy policzyć pole powierzchni bocznej, czyli pole prostokąta o wymiarach $8 π \times 6$ . Stąd $P_{b} = 48 π$ .

Uwaga!

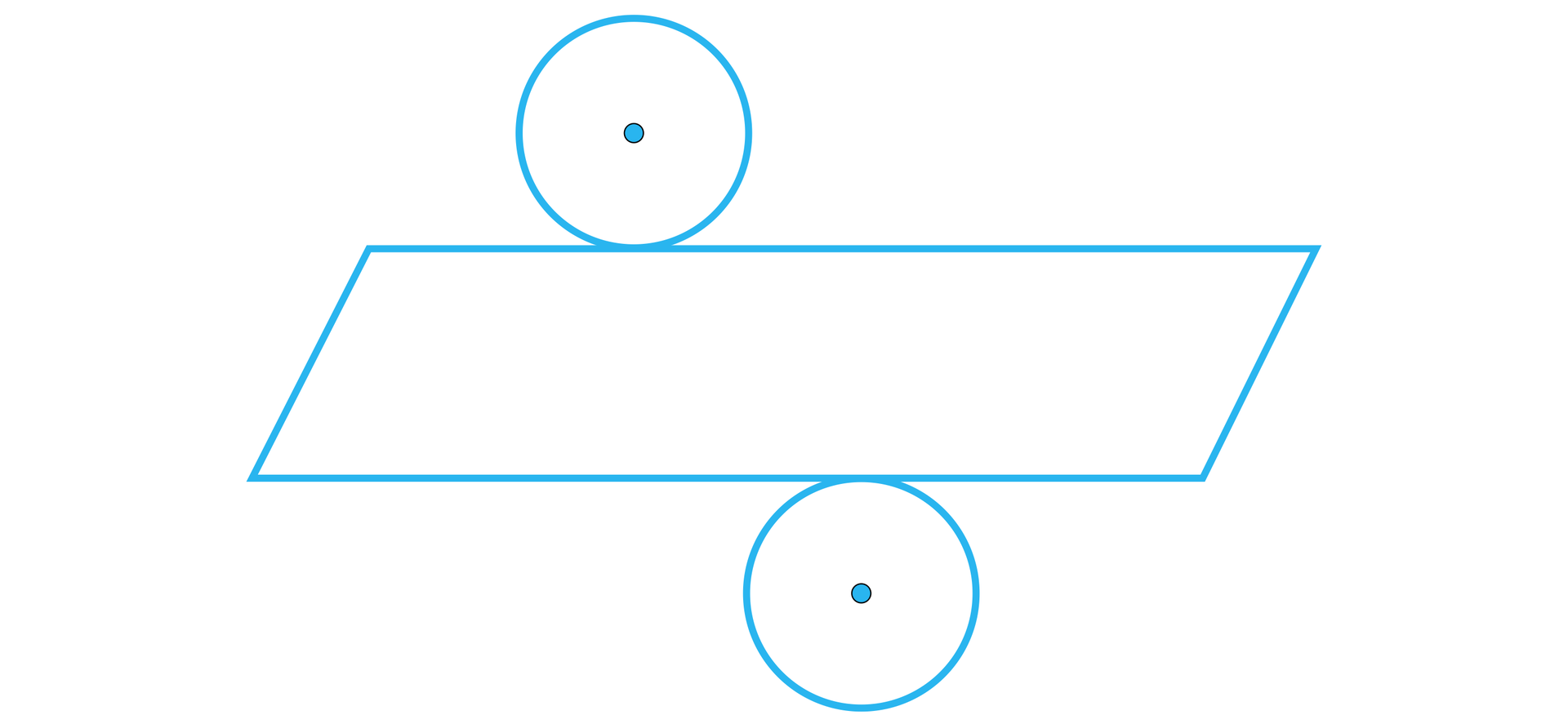
W siatce walca powierzchnia boczna może być również równoległobokiem innym niż prostokąt.

R1OJsLB41nxx9

Ilustracja przedstawia siatkę walca składającą się z równoległoboku oraz dwóch kół stycznych do dwóch dłuższych przeciwległych boków równoległoboku.

Słownik

walec

bryła obrotowa powstała przez obrót pewnego prostokąta wokół jednego z boków

wysokość walca

długość najkrótszego odcinka łączącego podstawy walca

Wprowadzenie

Aplet

Słownik