Wyznaczymy wszystkie dzielniki liczb $12$ i $30$.

Zbiór wszystkich dzielników liczby $12$: $D_{12}=\left\{1, 2, 3, 4, \mathrm{6,} 12\right\}$, zbiór wszystkich dzielników liczby $30$: $D_{30}=\left\{1, 2, 3, 5, 6, 10, 15, 30\right\}$. Widzimy, że wspólnymi dzielnikami są liczby: $1$, $2$, $3$, $6$.

Największym wspólnym dzielnikiem jest liczba $6$, co zapiszemy $NWD\left(12, 30\right)=6$.

Największy wspólny dzielnik liczb $6$ i $15$ to $3$. Łatwo to zauważyć, gdy rozważane liczby rozłożymy na czynniki pierwsze: $6=2\cdot 3$ oraz $15=5\cdot 3$. Jedynym wspólnym dzielnikiem (poza jedynką) jest liczba $3$.

Zatem $NWD\left(6, 15\right)=3$.

Największy wspólny dzielnik najłatwiej wyznacza się znając rozkład na czynniki pierwsze rozważanych liczb.

Wyznaczymy $NWD$ dla kilku zestawów liczb.

$NWD\left(2^3\cdot 5^2, 5\cdot 3^2\right)=5$, ponieważ $5$ to jedyny czynnik pierwszy, który dzieli każdą z liczb $2^3\cdot 5^2$ i $5\cdot 3^2$.

$NWD\left(2^3\cdot 5^2, 5\cdot 2^2\right)=5\cdot 2^2$, ponieważ $5$ oraz $2^2$ to największe potęgi liczb pierwszych, które dzielą każdą z liczb $2^3\cdot 5^2$ i $5\cdot 2^2$.

$NWD\left(3^2\cdot 2^5\cdot 7^3,5^3\cdot 3^4\cdot 7^6\right)=3^2\cdot 7^3=3087$, ponieważ $3^2$ oraz $7^3$ to największe potęgi liczb pierwszych występujące w rozkładach każdej z liczb $3^2\cdot 2^5\cdot 7^3$ i $5^3\cdot 3^4\cdot 7^6$.

$NWD\left(2^3\cdot 5^2, 5\cdot 2^2, 2^2\cdot 3^4\right)=2^2$, ponieważ $2^2$ to największa potęga liczby pierwszej, która wystepuje w rozkładzie każdej z liczb $2^3\cdot 5^2$, $5\cdot 2^2$ oraz $2^2\cdot 3^4$.

$NWD\left(2^5\cdot 7^3, 5^3\cdot 3^4\right)=1$, ponieważ liczby $2^5\cdot 7^3$ oraz $5^3\cdot 3^4$ nie mają żadnych wspólnych dzielników pierwszych.

Wyznaczymy największy wspólny dzielnik dla liczb $2520$ oraz $6750$.

Najpierw rozłożymy każdą z nich na czynniki pierwsze.

R956EX9C21DV6

Ilustracja przedstawia dwa przypadki rozkładu różnych liczb na czynniki pierwsze rozpatrzone obok siebie. Po lewej stronie zapisana jest liczba rozkładana, a po prawej jej dzielnik. Między dzielną a jej dzielnikiem znajduje się pionowa kreska. Rozkład liczby jest zapisany w dwóch pionowych kolumnach oddzielonych od siebie pionową kreską. W lewej części ilustracji rozłożona jest na czynniki liczba $2520$. Zapis jest następujący. Wiersz pierwszy od góry, lewa strona: $2520$, pionowa kreska, po prawej stronie zapisano dzielnik tej liczby, czyli $2$. Z dzielenia $2520:2$ otrzymujemy liczbę $1260$, którą zapisujemy w drugim wierszu na lewo, dalej kreska pionowa i na prawo dzielnik tej liczby, czyli $2$. W trzecim wierszu na lewo zapisujemy wynik dzielenia, czyli liczbę $630$, pionowa kreska i na prawo kolejny dzielnik, czyli znowu $2$. W czwartym wierszu zapisujemy liczbę $315$, kreska pionowa, na prawo jej dzielnik $5$. Wiersz piąty: na lewo liczba $63$, kreska pionowa, na prawo jej dzielnik, czyli $3$. Wiersz szósty: na lewo liczba $21$, kreska pionowa, na prawo jej dzielnik, czyli liczba $3$. Wiersz siódmy: na lewo liczba $7$, kreska pionowa, na prawo jej dzielnik, czyli liczba $7$. Wiersz ósmy: na lewo liczba $1$, kreska pionowa, na prawo nie zapisujemy nic, zostawiamy puste miejsce. W prawej części ilustracji analogicznie rozłożona na czynniki jest liczba $6750$. Jej rozkład jest następujący. Wiersz pierwszy: na lewo liczba $6750$, pionowa kreska, na prawo jej dzielnik liczba $5$. Wiersz drugi: na lewo liczba $1350$, pionowa kreska, na prawo jej dzielnik liczba $5$. Wiersz trzeci: na lewo liczba $270$, pionowa kreska, na prawo jej dzielnik liczba $3$. Wiersz czwarty: na lewo liczba $90$, pionowa kreska, na prawo jej dzielnik liczba $3$. Wiersz piąty: na lewo liczba $30$, pionowa kreska, na prawo jej dzielnik liczba $3$. Wiersz szósty: na lewo liczba $10$, pionowa kreska, na prawo jej dzielnik liczba $2$. Wiersz siódmy: na lewo liczba $5$, pionowa kreska, na prawo jej dzielnik liczba $5$. Wiersz ósmy: na lewo liczba $1$, pionowa kreska, na prawo puste miejsce.

Sprawdźmy, które liczby pierwsze powtarzają się w rozkładach każdej z danych liczb.

R113L34E12FB6

Ilustracja przedstawia rozkłady dwóch różnych liczb na czynniki pierwsze rozpatrzone obok siebie. Wspólne dzielniki obu liczb oznaczono, obrysowując je kółkiem. Po lewej stronie zapisana jest liczba rozkładana, a po prawej jej dzielnik. Między dzielną a jej dzielnikiem znajduje się pionowa kreska. Rozkład liczby jest zapisany w dwóch pionowych kolumnach oddzielonych od siebie pionową kreską. W lewej części ilustracji rozłożona jest na czynniki liczba $2520$. Zapis jest następujący. Wiersz pierwszy od góry, lewa strona: $2520$, pionowa kreska, po prawej stronie zapisano dzielnik tej liczby, czyli $2$. Dzielnik ten zaznaczono, obrysowując go kółkiem. Z dzielenia $2520:2$ otrzymujemy liczbę $1260$, którą zapisujemy w drugim wierszu po lewo, dalej kreska pionowa i na prawo dzielnik tej liczby, czyli $2$. W trzecim wierszu na lewo zapisujemy wynik dzielenia, czyli liczbę $630$, pionowa kreska i na prawo kolejny dzielnik, czyli znowu $2$. W czwartym wierszu zapisujemy liczbę $315$, kreska pionowa, na prawo jej dzielnik $5$, który obrysowano kółkiem. Wiersz piąty: na lewo liczba $63$, kreska pionowa, na prawo jej dzielnik, czyli $3$, który obrysowano kółkiem. Wiersz szósty: na lewo liczba $21$, kreska pionowa, na prawo jej dzielnik, czyli liczba $3$, który obrysowano kółkiem. Wiersz siódmy: na lewo liczba $7$, kreska pionowa, na prawo jej dzielnik, czyli liczba $7$. Wiersz ósmy: na lewo liczba $1$, kreska pionowa, na prawo nie zapisujemy nic, zostawiamy puste miejsce. W prawej części ilustracji analogicznie rozłożona na czynniki jest liczba $6750$. Jej rozkład jest następujący. Wiersz pierwszy: na lewo liczba $6750$, pionowa kreska, na prawo jej dzielnik liczba $5$ obrysowana kółkiem. Wiersz drugi: na lewo liczba $1350$, pionowa kreska, na prawo jej dzielnik liczba $5$. Wiersz trzeci: na lewo liczba $270$, pionowa kreska, na prawo jej dzielnik liczba $3$. Wiersz czwarty: na lewo liczba $90$, pionowa kreska, na prawo jej dzielnik liczba $3$ obrysowana kółkiem. Wiersz piąty: na lewo liczba $30$, pionowa kreska, na prawo jej dzielnik liczba $3$ obrysowana kółkiem. Wiersz szósty: na lewo liczba $10$, pionowa kreska, na prawo jej dzielnik liczba $2$ obrysowana kółkiem. Wiersz siódmy: na lewo liczba $5$, pionowa kreska, na prawo jej dzielnik liczba $5$. Wiersz ósmy: na lewo liczba $1$, pionowa kreska, na prawo puste miejsce.

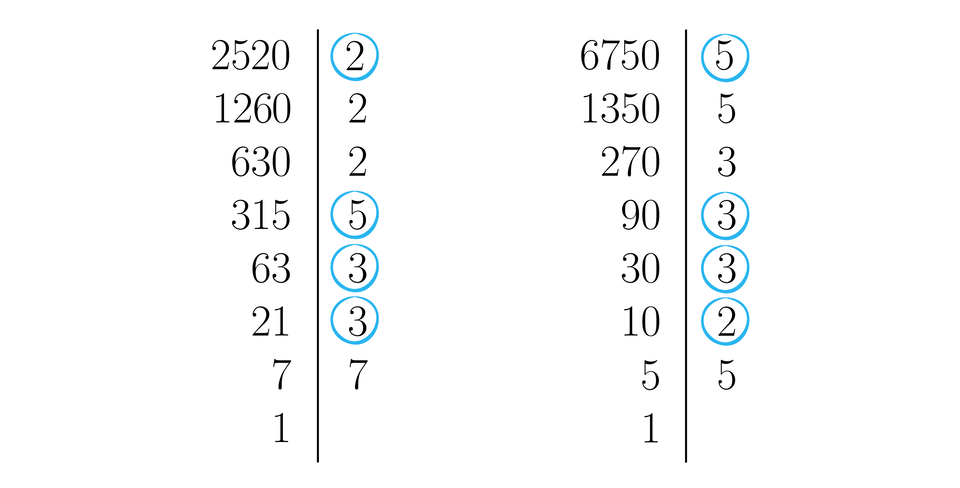
W obu rozkładach powtarzają się: liczba $5$, druga potęga liczby $3$ oraz liczba $2$.

Oznacza to, że $NWD\left(2520, 6750\right)=NWD\left(2^3\cdot 3^2\cdot 5\cdot 7, 2\cdot 3^3\cdot 5^3\right)=2\cdot 3^2\cdot 5=90$.

Wyznaczymy największy wspólny dzielnik dla liczb $3150$, $2205$ oraz $900$.

Najpierw rozłożymy każdą z nich na czynniki pierwsze:

RQpGKPudb4cQQ

Ilustracja przedstawia trzy rozkłady różnych liczb na czynniki pierwsze rozpatrzone obok siebie. Po lewej stronie zapisana jest liczba rozkładana, a po prawej jej dzielnik. Między dzielną a jej dzielnikiem znajduje się pionowa kreska. Rozkład liczby jest zapisany w dwóch pionowych kolumnach oddzielonych od siebie pionową kreską. W lewej części ilustracji rozłożona jest na czynniki liczba $3150$. Wiersz pierwszy od góry, lewa strona: $3150$, pionowa kreska, po prawej stronie zapisano dzielnik tej liczby, czyli $2$. Drugi wiersz: po lewo liczba $1575$., dalej kreska pionowa i po prawo dzielnik tej liczby, czyli $5$. W trzecim wierszu po lewo zapisano liczbę $315$, pionowa kreska i po prawo kolejny dzielnik, czyli $5$. W czwartym wierszu zapisano liczbę $63$, kreska pionowa, po prawo jej dzielnik $3$. Wiersz piąty: po lewo liczba $21$, kreska pionowa, po prawo jej dzielnik, czyli liczba $3$. Wierz szósty: po lewo liczba $7$, kreska pionowa, po lewo jej dzielnik, czyli liczba $7$. Wiersz siódmy: po lewo liczba $1$, kreska pionowa, po prawo puste miejsce. W środkowej części ilustracji analogicznie rozłożona na czynniki jest liczba $2205$. Jej rozkład jest następujący. Wiersz pierwszy: po lewo liczba $2205$, pionowa kreska, po prawo jej dzielnik liczba $5$. Wiersz drugi: po lewo liczba $441$, pionowa kreska, po prawo jej dzielnik liczba $3$. Wiersz trzeci: po lewo liczba $147$, pionowa kreska, po prawo jej dzielnik liczba $3$. Wiersz czwarty: po lewo liczba $49$, pionowa kreska, po prawo jej dzielnik liczba $7$. Wiersz piąty: po lewo liczba $7$, pionowa kreska, po prawo jej dzielnik liczba $7$. Wiersz szósty: po lewo liczba $1$, pionowa kreska, po prawo puste miejsce. W prawej części ilustracji analogicznie rozłożona na czynniki jest liczba $900$. Jej rozkład jest następujący. Wiersz pierwszy: po lewo liczba $900$, pionowa kreska, po prawo jej dzielnik liczba $2$. Wiersz drugi: po lewo liczba $450$, pionowa kreska, po prawo jej dzielnik liczba $2$. Wiersz trzeci: po lewo liczba $225$, pionowa kreska, po prawo jej dzielnik liczba $3$. Wiersz czwarty: po lewo liczba $75$, pionowa kreska, po prawo jej dzielnik liczba $3$. Wiersz piąty: po lewo liczba $25$, pionowa kreska, po prawo jej dzielnik liczba $5$. Wiersz szósty: po lewo liczba $5$, pionowa kreska, po prawo jej dzielnik liczba $5$. Wiersz siódmy: po lewo liczba $1$, pionowa kreska, po prawo puste miejsce.

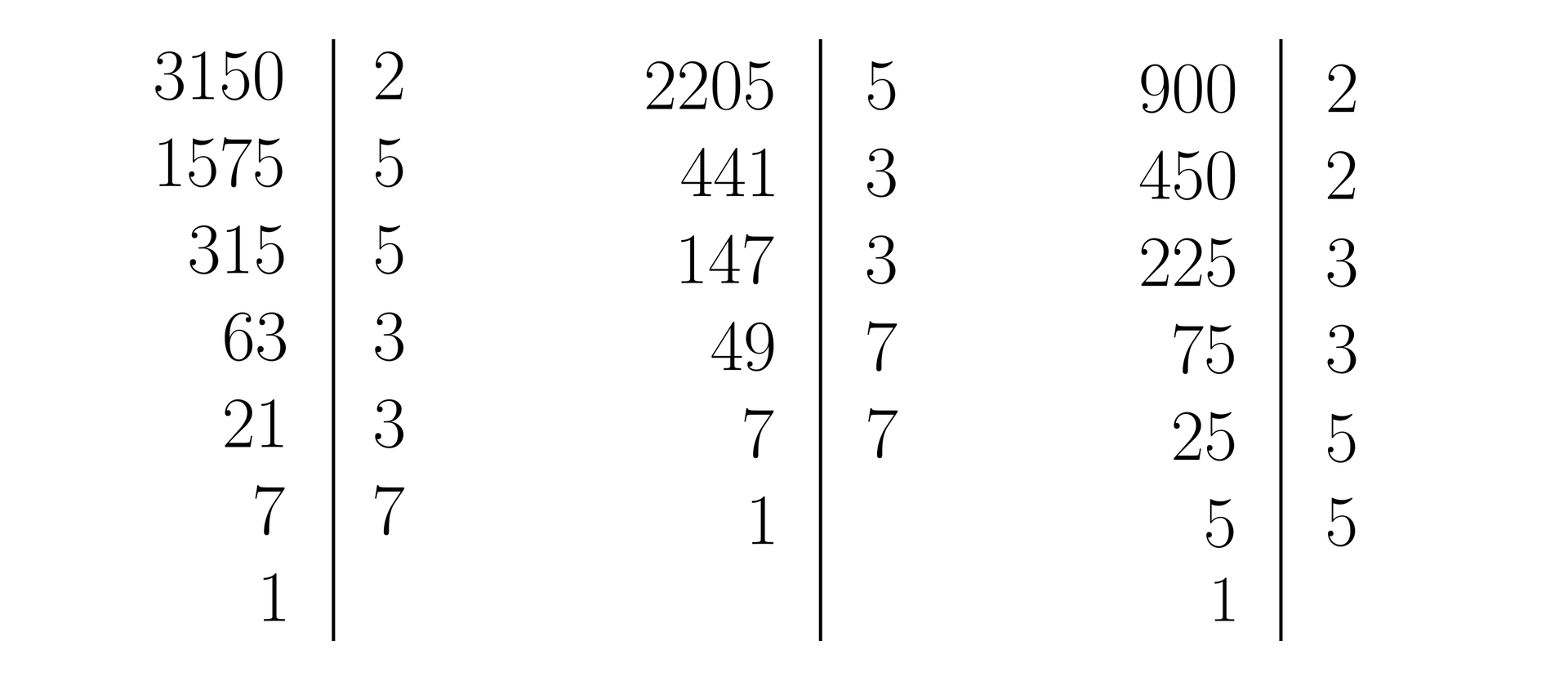
Sprawdźmy, które liczby pierwsze powtarzają się w rozkładach każdej z danych liczb.

Ry1CUyeNKzFCN

Ilustracja przedstawia trzy rozkłady różnych liczb na czynniki pierwsze rozpatrzone obok siebie. Powtarzające się czynniki pierwsze z rozkładów wszystkich liczb wyróżniono, obrysowując je kółkami. Po lewej stronie zapisana jest liczba rozkładana, a po prawej jej dzielnik. Między dzielną a jej dzielnikiem znajduje się pionowa kreska. Rozkład liczby jest zapisany w dwóch pionowych kolumnach oddzielonych od siebie pionową kreską. W lewej części ilustracji rozłożona jest na czynniki liczba $3150$. Wiersz pierwszy od góry, lewa strona: $3150$, pionowa kreska, po prawej stronie zapisano dzielnik tej liczby, czyli $2$. Drugi wiersz: po lewo liczba $1575$., dalej kreska pionowa i po prawo dzielnik tej liczby, czyli $5$. W trzecim wierszu po lewo zapisano liczbę $315$, pionowa kreska i po prawo kolejny dzielnik, czyli $5$, który obrysowano kółkiem. W czwartym wierszu zapisano liczbę $63$, kreska pionowa, po prawo jej dzielnik $3$, który obrysowano kółkiem. Wiersz piąty: po lewo liczba $21$, kreska pionowa, po prawo jej dzielnik, czyli liczba $3$, który obrysowano kółkiem. Wierz szósty: po lewo liczba $7$, kreska pionowa, po lewo jej dzielnik, czyli liczba $7$. Wiersz siódmy: po lewo liczba $1$, kreska pionowa, po prawo puste miejsce. W środkowej części ilustracji analogicznie rozłożona na czynniki jest liczba $2205$. Jej rozkład jest następujący. Wiersz pierwszy: po lewo liczba $2205$, pionowa kreska, po prawo jej dzielnik liczba $5$, który obrysowano kółkiem. Wiersz drugi: po lewo liczba $441$, pionowa kreska, po prawo jej dzielnik liczba $3$, który obrysowano kółkiem. Wiersz trzeci: po lewo liczba $147$, pionowa kreska, po prawo jej dzielnik liczba $3$, który obrysowano kółkiem. Wiersz czwarty: po lewo liczba $49$, pionowa kreska, po prawo jej dzielnik liczba $7$. Wiersz piąty: po lewo liczba $7$, pionowa kreska, po prawo jej dzielnik liczba $7$. Wiersz szósty: po lewo liczba $1$, pionowa kreska, po prawo puste miejsce. W prawej części ilustracji analogicznie rozłożona na czynniki jest liczba $900$. Jej rozkład jest następujący. Wiersz pierwszy: po lewo liczba $900$, pionowa kreska, po prawo jej dzielnik liczba $2$. Wiersz drugi: po lewo liczba $450$, pionowa kreska, po prawo jej dzielnik liczba $2$. Wiersz trzeci: po lewo liczba $225$, pionowa kreska, po prawo jej dzielnik liczba $3$, który obrysowano kółkiem. Wiersz czwarty: po lewo liczba $75$, pionowa kreska, po prawo jej dzielnik liczba $3$, który obrysowano kółkiem. Wiersz piąty: po lewo liczba $25$, pionowa kreska, po prawo jej dzielnik liczba $5$, który obrysowano kółkiem. Wiersz szósty: po lewo liczba $5$, pionowa kreska, po prawo jej dzielnik liczba $5$. Wiersz siódmy: po lewo liczba $1$, pionowa kreska, po prawo puste miejsce.

We wszystkich rozkładach powtarzają się: liczba $5$ oraz druga potęga liczby $3$.

Oznacza to, że $NWD\left(3150, 2205, 900\right)=NWD\left(2\cdot 3^2\cdot 5^2\cdot 7, 3^2\cdot 5\cdot 7^2, 2^2\cdot 3^2\cdot 5^2\right)=$

$=5\cdot 3^2=45$

Mówimy, że dwie (lub więcej) liczby naturalne są to liczby względnie pierwszeliczby względnie pierwszeliczby względnie pierwsze, jeśli ich największy wspólny dzielniknajwiększy wspólny dzielniknajwiększy wspólny dzielnik jest równy $1$.

Liczby $10$ i $15$ nie są względnie pierwsze, ponieważ $NWD\left(10, 15\right)=5 > 1$.

Liczby $10$ i $21$ są względnie pierwsze, ponieważ $NWD\left(10, 21\right)=1$

Liczby $6$, $10$ i $15$ są względnie pierwsze, ponieważ $NWD\left(6, 10, 15\right)=1$.

Liczby $6$, $10$ i $15$ nie są parami względnie pierwsze, ponieważ można wybrać z nich parę liczb, które nie są względnie pierwsze, np. $NWD\left(6, 10\right)=2$.

Liczby $26$, $33$ i $35$ są względnie pierwsze, ponieważ $NWD\left(26, 33, 35\right)=1$.

Liczby $26$, $33$ i $35$ są parami względnie pierwsze, ponieważ każde dwie spośród nich są względnie pierwsze: $NWD\left(26, 33\right)=1$, $NWD\left(33, 35\right)=1$, $NWD\left(26, 35\right)=1$.

Wyznaczymy największy wspólny dzielnik liczb $984$ i $1435$.

Ponieważ największy wspólny dzielnik dwóch liczb naturalnych dzieli również ich różnicę, więc $NWD\left(984, 1435\right)=d$ dzieli liczbę $1435-984=451$.

Ponieważ $d$ dzieli liczby $984$ i $451$, to dzieli również ich różnicę $984-451=533$ $\left(\ast\right)$.

Zatem $d$ dzieli liczby $533$ i $451$, czyli podzieli również ich różnicę $533-451=82$.

Teraz wiemy już, że $d$ dzieli liczby $451$ i $82$, stąd $d$ dzieli $451-82=369$ $\left(\ast\ast\right)$.

Ponieważ $d$ dzieli liczby $369$ i $82$, więc dzieli również $369-82=287$.

Wiadomo, że $d$ dzieli liczby $287$ i $82$, zatem dzieli też $287-82=205$.

Skoro $d$ dzieli liczby $205$ i $82$, to dzieli również $205-82=123$.

Ponieważ $d$ dzieli liczby $123$ i $82$, więc dzieli też $123-82=41$.

Teraz można już zauważyć, że skoro $d$ dzieli $82$ i $41$ i jest największym z możliwych wspólnych dzielników tych liczb, to $d=41$.

Zwróć uwagę, że powyższe rozwiązanie można było skrócić. W miejscu oznaczonym $\left(\ast\right)$ zamiast od liczby $984$ odejmować liczbę $451$ można było odjąć jej dwukrotność, czyli $2\cdot 451=902$. Jako argument pozwalający na odejmowanie z takim rozmachem wystarczy przywołać fakt, że jeśli $d$ dzieli liczbę, to podzieli również jej wielokrotność. Zatem w miejscu $\left(\ast\right)$ wykonamy odejmowanie $984-2\cdot 451=984-902=82$. Zgodnie ze sposobem opisanym powyżej wykonalibyśmy odejmowanie liczb $451$ i $82$ tak jak w miejscu $\left(\ast\ast\right)$, ale tu również możemy zaoszczędzić trochę czasu i zauważyć, że zamiast od $451$ odejmować $82$, rozwiązanie przyspieszy odjęcie wielokrotność liczby $82$, konkretnie $5\cdot 82=410$. Czyli $d$ dzieli $451-5\cdot 82=451-410=41$. Końcówka rozwiązania pozostaje bez zmian. Jeśli zauważymy, że $d$ jest największym dzielnikiem liczb $41$ i $82$, to dojdziemy do wniosku, że $d=41$.

Prześledźmy kolejne wykonane operacje:

Wyznaczymy największy wspólny dzielnik liczb $965$ i $1230$.

skończony ciąg jasno zdefiniowanych operacji (czynności), które mają doprowadzić do rozwiązania konkretnego problemu, osiągnięcia wyznaczonego celu; cechą charakterystyczną jest jego powtarzalność i niezawodność w pewnych z góry zdefiniowanych warunkach; przy pewnych założeniach prowadzi niezawodnie (choć niekoniecznie optymalnie) od stanu $A$ do stanu $B$

największy wspólny dzielnik liczb naturalnych $a$ i $b$ to największa liczba naturalna dzieląca liczby $a$ i $b$; oznaczamy go przez $NWD\left(a, b\right)$; pojęcie można analogicznie zdefiniować dla dowolnie wielu liczb naturalnych

mówimy, że liczby naturalne $a$ i $b$ są względnie pierwsze, gdy ich największy wspólny dzielnik jest równy $1$; pojęcie można analogicznie zdefiniować dla dowolnie wielu liczb naturalnych