R1Dj0sGR63t0U

Ilustracja przedstawia graniastosłup o podstawie trójkąta. Wszystkie krawędzie podstawy podpisano literą a, krawędź boczną ostrosłupa podpisano literą h.

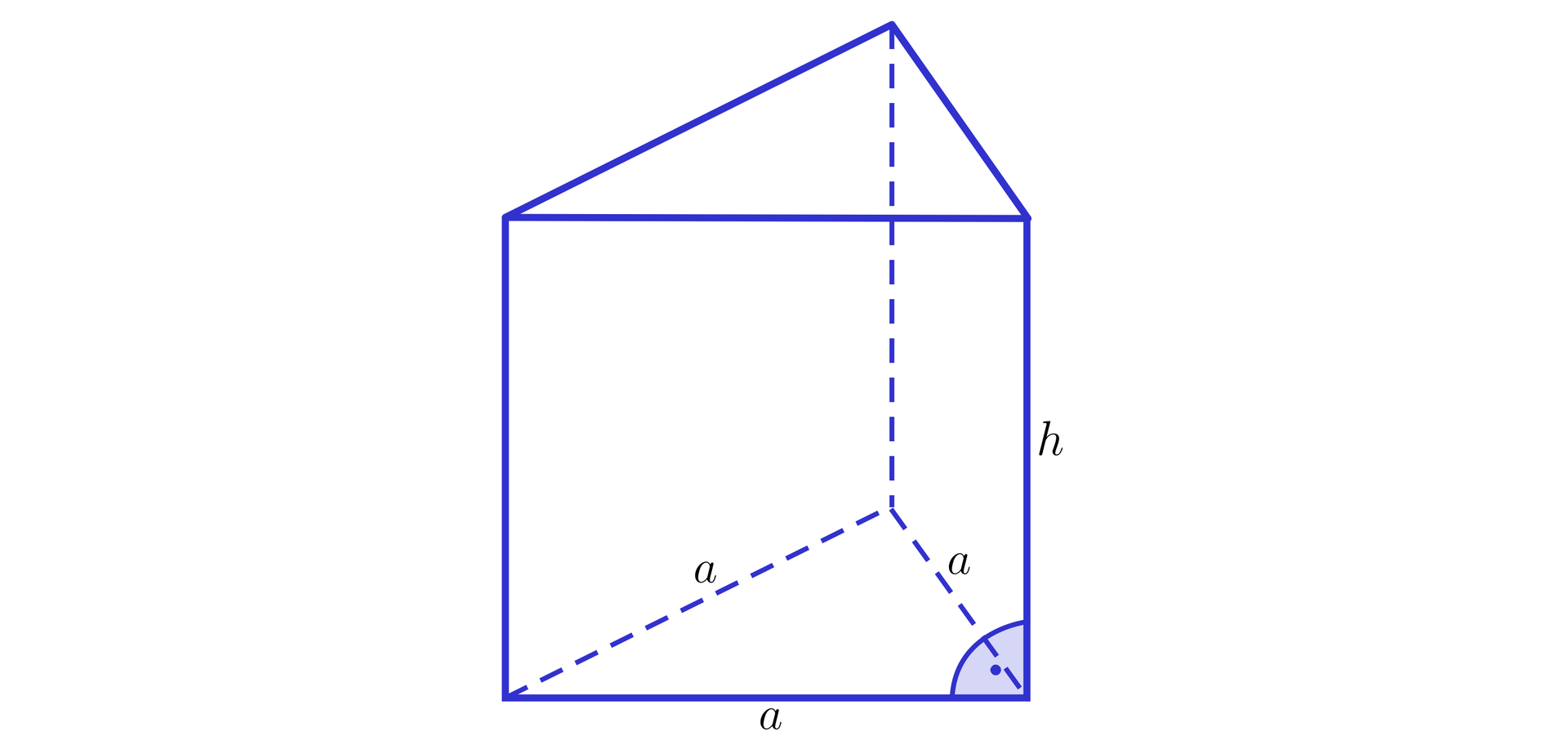
Pole powierzchni całkowitej graniastosłupa prawidłowego trójkątnego definiujemy jako sumę pól jego podstaw i pola powierzchni bocznej. Wobec tego pole powierzchni całkowitej graniastosłupa prawidłowego trójkątnego jest równe polu jego siatkisiatka graniastosłupa prawidłowego trójkątnegosiatki. Zależność tę opisuje wzór:

gdzie $h$ jest długością wysokości graniastosłupa prawidłowego trójkątnego, $a$ jest długością krawędzi podstawy graniastosłupa prawidłowego trójkątnego.

Obliczymy pole powierzchni całkowitej graniastosłupa prawidłowego trójkątnegograniastosłup prawidłowy trójkątnygraniastosłupa prawidłowego trójkątnego dla którego przekątna ściany bocznej ma długość $0,5$ i jest nachylona do krawędzi podstawy pod kątem, którego tangens jest równy $\frac{\sqrt{3}}{2}$.

Rozwiązanie:

R16p5os9HxkP1

Ilustracja przedstawia graniastosłup o podstawie trójkąta. Wierzchołki dolnej podstawy to A B oraz C, a wierzchołki górnej podstawy podpisano D E F. W ścianie bocznej graniastosłupa zaznaczono jej przekątną AF, kąt CAF podpisano literą alfa. Wszystkie krawędzie podstawy podpisano literą a, krawędź boczną ostrosłupa podpisano literą h.

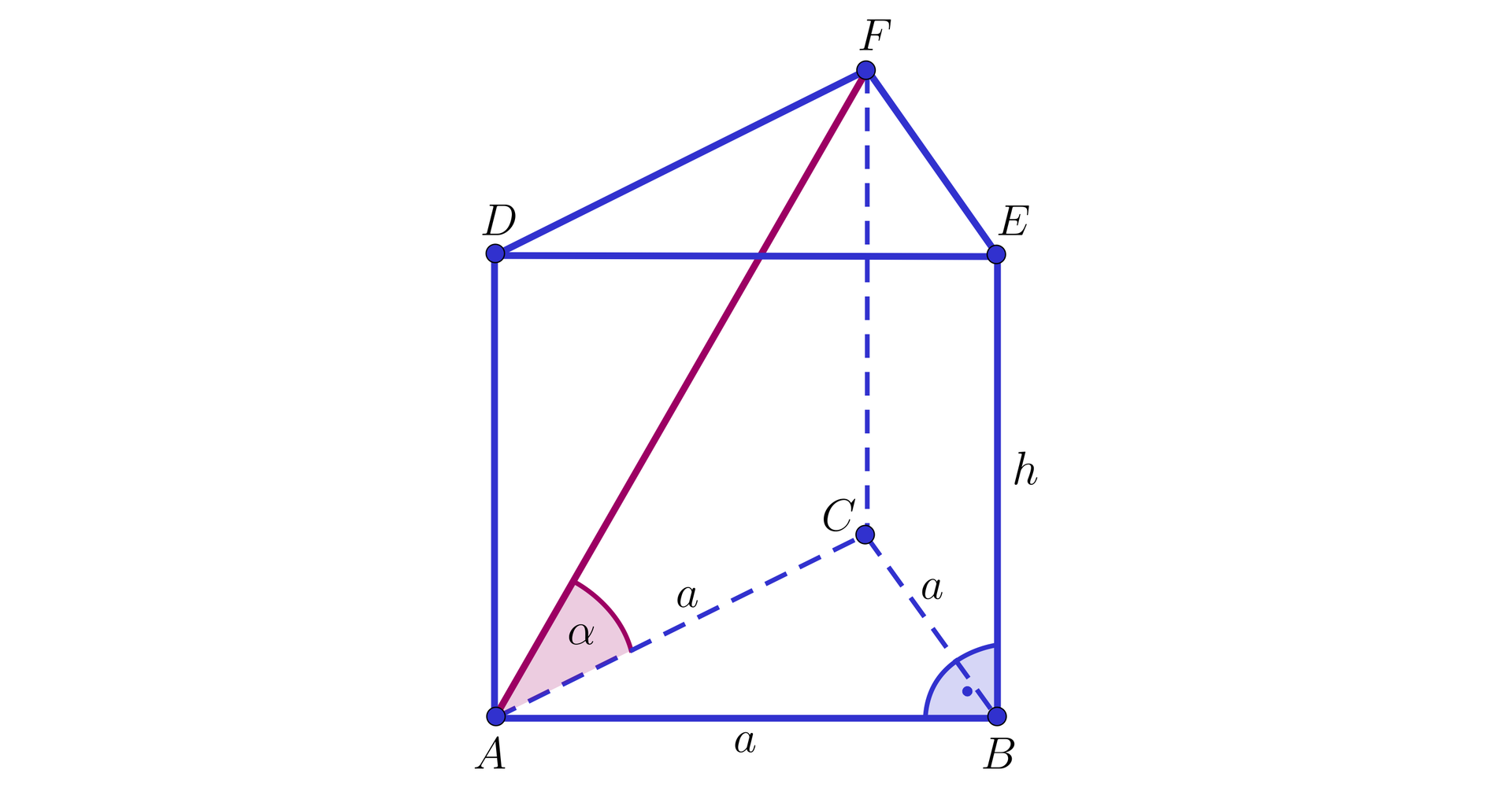
Niech $a>0$ oznacza długość krawędzi podstawy oraz $h>0$ długość wysokości rozważanego graniastosłupa.

Z warunków zadania mamy kolejno

$\mathrm{tg}\alpha =\frac{\left|FC\right|}{\left|AC\right|}$,

$\frac{h}{a}=\frac{\sqrt{3}}{2}$,

$h=\frac{\sqrt{3}}{2}a$.

Zastosujemy twierdzenie Pitagorasatwierdzenie Pitagorasatwierdzenie Pitagorasa do trójkąta $ACF$ podstawiając jednocześnie zależność $h=\frac{\sqrt{3}}{2}a$. Otrzymujemy kolejno

$a^2+\frac{3}{4}{a}^2=\frac{1}{4}$,

$a^2=\frac{1}{7}$,

$a=\frac{\sqrt{7}}{7}$.

Stąd $h=\frac{\sqrt{21}}{14}$. Możemy obliczyć pole powierzchni całkowitej naszego graniastosłupa

$P_{pc}=\frac{a^2\sqrt{3}}{2}+3ah=\frac{{\left({\displaystyle \frac{\sqrt{7}}{7}}\right)}^2·\sqrt{3}}{2}+3·\frac{\sqrt{7}}{7}·\frac{\sqrt{21}}{14}=\frac{2\sqrt{3}}{7}$.

O graniastosłupie prawidłowym trójkątnym wiadomo, że kosinus kąta między przekątną ściany bocznej i krawędzią podstawy wynosi $\frac{3\sqrt{10}}{10}$ oraz promień okręgu opisanego na podstawie graniastosłupa wynosi $4\sqrt{3}$. Obliczymy pole powierzchni całkowitej tego graniastosłupa.

Rozwiązanie:

RILNolhBNZvlC

Ilustracja przedstawia graniastosłup o podstawie trójkąta. Wierzchołki dolnej podstawy to A B oraz C, a wierzchołki górnej podstawy podpisano D E F. W ścianie bocznej graniastosłupa zaznaczono jej przekątną AF, kąt CAF podpisano literą alfa. Wszystkie krawędzie podstawy podpisano literą a, krawędź boczną ostrosłupa podpisano literą h. Obok graniastosłupa znajduje się trójkąt A B C wpisany w okrąg, boki trójkąta mają długość a, z każdego wierzchołka trójkąta poprowadzono promień, który podpisano literą R.

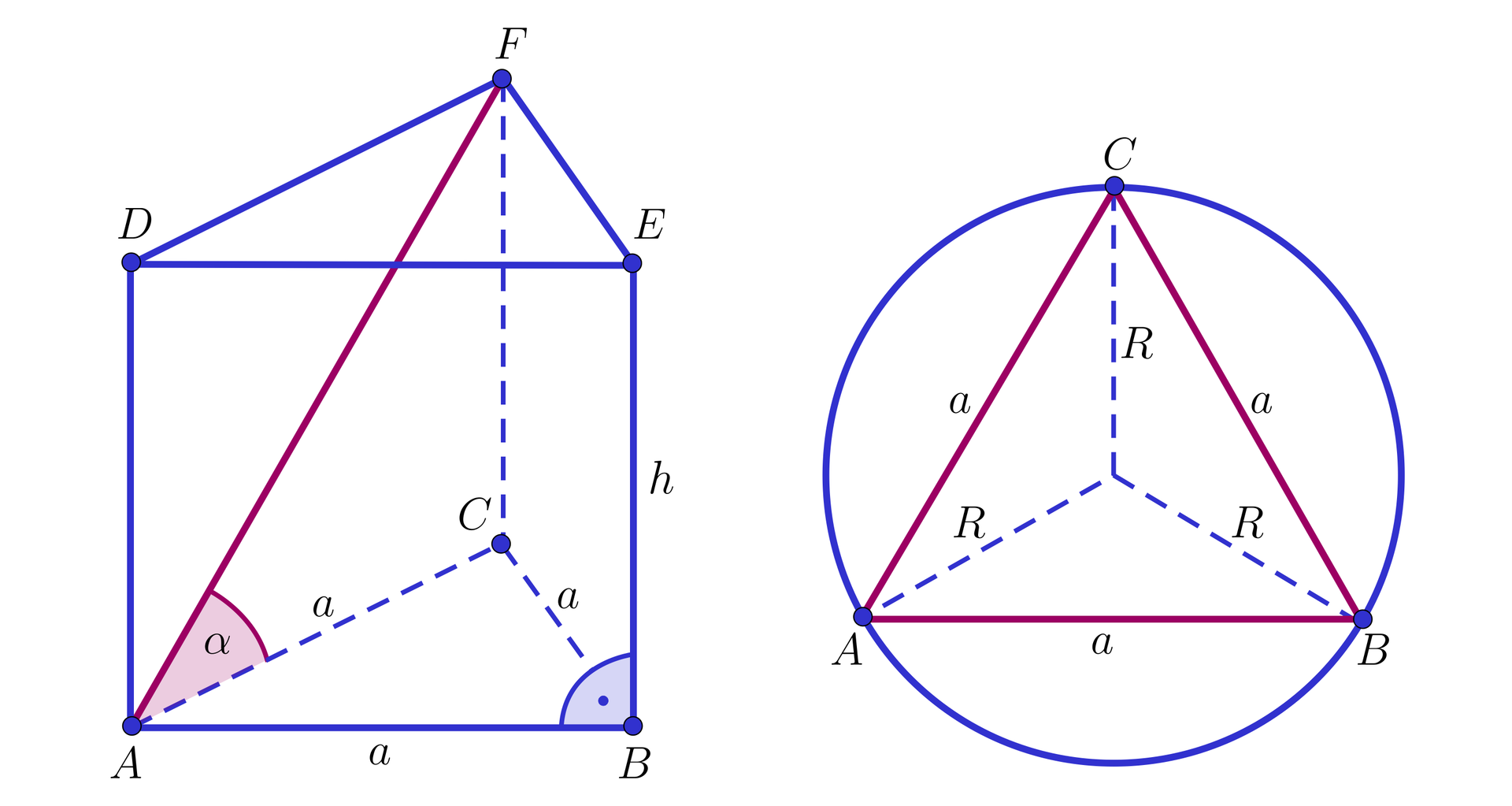
Niech $a>0$ oznacza długość krawędzi podstawy, $h>0$ długość wysokości oraz $d>0$ długość przekątnej ściany bocznej rozważanego graniastosłupa. Promień okręgu opisanego na trójkącie równobocznym stanowi $\frac{2}{3}$ wysokości podstawy graniastosłupa, zatem otrzymujemy $\frac{a\sqrt{3}}{2}·\frac{2}{3}=4\sqrt{3}$, czyli $a=12$.

Z warunków zadania mamy

$\cos \alpha =\frac{\left|AC\right|}{\left|AF\right|}$,

$\frac{a}{d}=\frac{3\sqrt{10}}{10}$,

$\frac{12}{d}=\frac{3\sqrt{10}}{10}$,

$d=4\sqrt{10}$.

Wyliczymy teraz długość wysokości graniastosłupa. Zastosujemy twierdzenie Pitagorasa do trójkąta $ACF$. Otrzymujemy kolejno

$d^2=a^2+h^2$,

$160=144+h^2$,

$h=4$.

Możemy obliczyć pole powierzchni całkowitej naszego graniastosłupa

$P_{pc}=\frac{a^2\sqrt{3}}{2}+3ah=\frac{{12}^2·\sqrt{3}}{2}+3·12·4=72\sqrt{3}+144$.

Graniastosłup prawidłowy trójkątny o objętości $24\sqrt{3}$ przecięto płaszczyzną przechodzącą przez krawędź podstawy i jeden z wierzchołków drugiej podstawy, tak, że tworzy ona z płaszczyzną podstawy kąt, którego $\mathrm{tg}\alpha =\sqrt{3}$. Obliczymy pole powierzchni całkowitej tego graniastosłupa.

R1XmPgVNcF2De

Ilustracja przedstawia graniastosłup o podstawie trójkąta. Wierzchołki dolnej podstawy to A B oraz C, a wierzchołki górnej podstawy podpisano D E F. W ścianie bocznej graniastosłupa zaznaczono jej przekątną AF, kąt CAF podpisano literą alfa. Wszystkie krawędzie podstawy podpisano literą a, krawędź boczną ostrosłupa podpisano literą h. W ścianie bocznej graniastosłupa zaznaczono jej przekątną AF, w drugiej ścianie ocznej zaznaczono jej przekątną BF. W podstawie zaznaczono odcinek CG, przy czym punkt G leży na krawędzi AB. W graniastosłupie zaznaczono również odcinek FG, kąt CGF podpisano literą alfa.

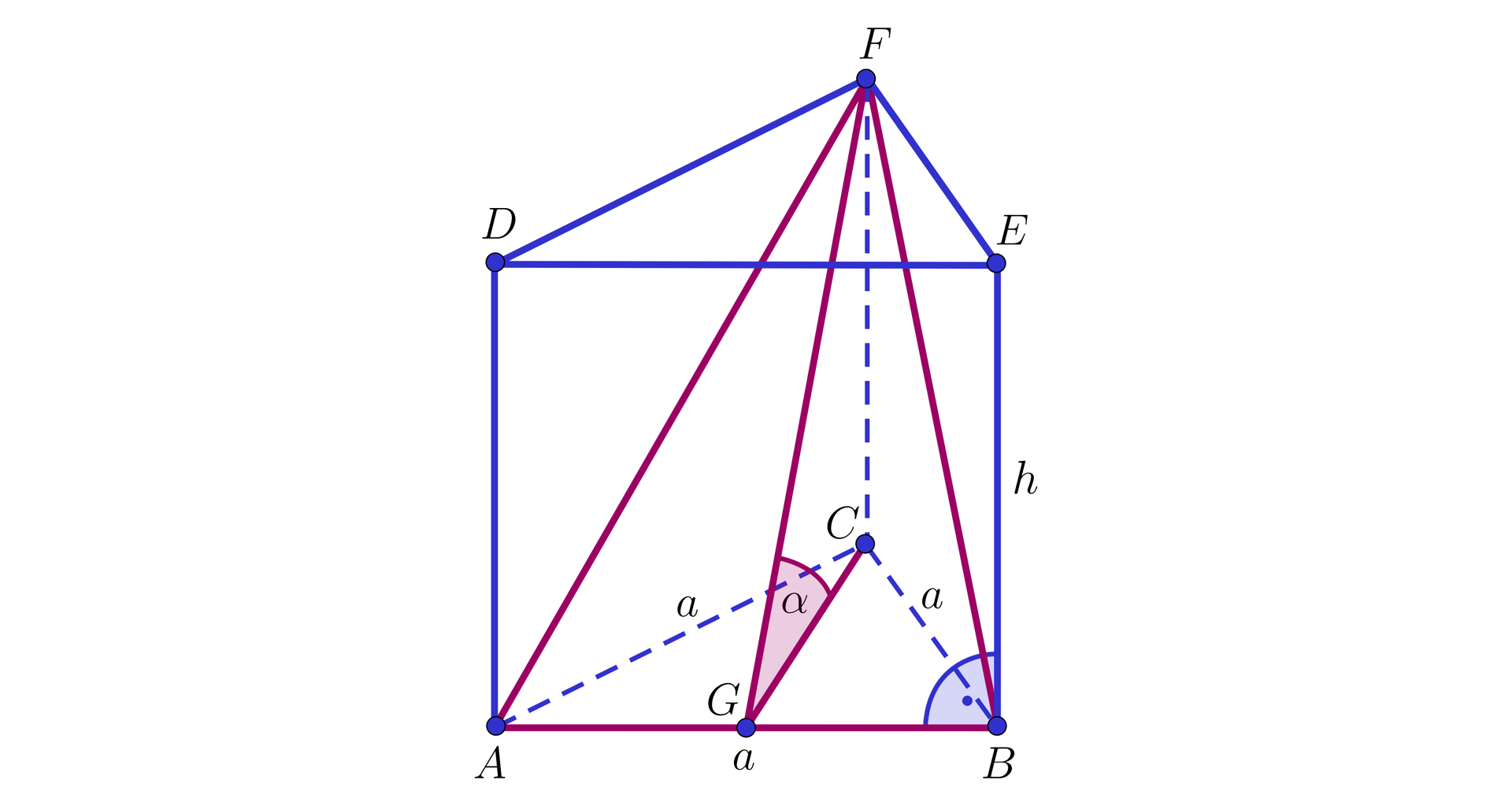
Rozwiązanie:

Niech $a>0$ oznacza długość krawędzi podstawy oraz $h>0$ długość wysokości rozważanego graniastosłupa. Z warunków zadania mamy kolejno

$\mathrm{tg}\alpha =\frac{\left|FC\right|}{\left|GC\right|}$,

$\frac{h}{{\displaystyle \frac{a\sqrt{3}}{2}}}=\sqrt{3}$,

$h=\frac{3}{2}a$.

Następnie mamy

$V=\frac{a^2\sqrt{3}}{4}h$,

$\frac{a^2\sqrt{3}}{4}·\frac{3}{2}a=24\sqrt{3}$,

$\frac{3a^3\sqrt{3}}{8}=24\sqrt{3}$,

$a^3=64$,

$a=4$.

Wyliczymy teraz długość wysokości graniastosłupa $h=\frac{3}{2}a=6$. Możemy obliczyć pole powierzchni całkowitej naszego graniastosłupa

$P_{pc}=\frac{a^2\sqrt{3}}{2}+3ah=\frac{4^2·\sqrt{3}}{2}+3·4·6=8\sqrt{3}+72$.

W graniastosłupie prawidłowym trójkątnym sinus kąta jaki tworzy przekątna ściany bocznej z sąsiednią ścianą boczną wynosi $\frac{1}{4}$. Objętość graniastosłupa jest równa $\frac{\sqrt{33}}{4}$. Obliczymy pole powierzchni całkowitej tego graniastosłupa.

Rozwiązanie:

RoACevWtIPCJk

IlustracjaIlustracja przedstawia graniastosłup o podstawie trójkąta. Wierzchołki dolnej podstawy to A B oraz C, a wierzchołki górnej podstawy podpisano D E F. Na krawędzi BC zaznaczono punkt P. W graniastosłupie zaznaczono trójkąt prostokątny APF. Kąt APF to kąt prosty, kąt PFA podpisano literą alfa.

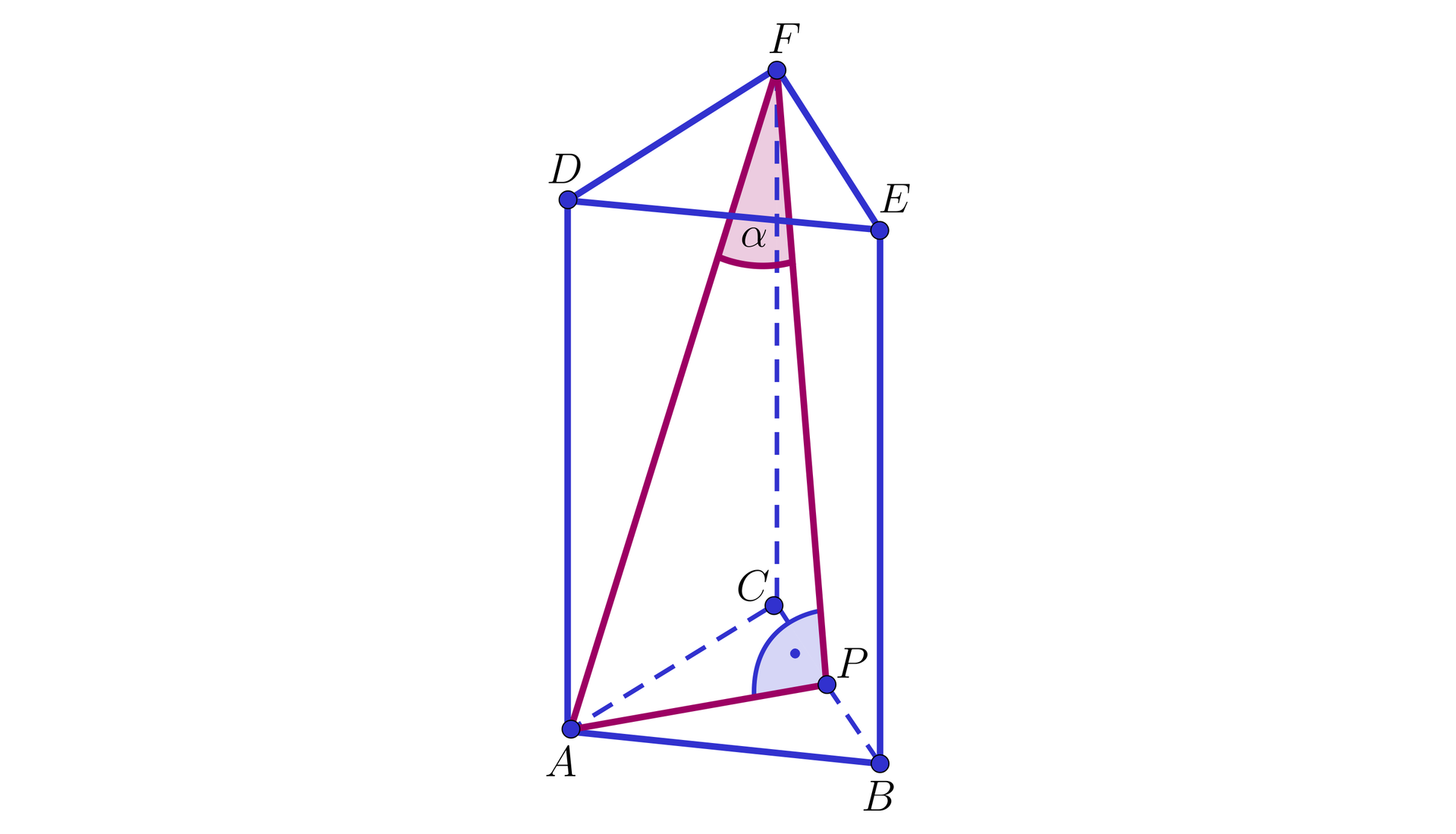
Niech $a>0$ oznacza długość krawędzi podstawy, $h>0$ długość wysokości oraz $d>0$ długość przekątnej ściany bocznej rozważanego graniastosłupa. Trójkąt $APF$ jest prostokątny. Odcinek $\left|CP\right|=\frac{1}{2}a$ oraz $\left|AP\right|=\frac{a\sqrt{3}}{2}$. Z warunków zadania mamy kolejno

$\sin \alpha =\frac{\left|AP\right|}{\left|AF\right|}$,

$\frac{{\displaystyle \frac{a\sqrt{3}}{2}}}{d}=\frac{1}{4}$,

$d=2\sqrt{3}a$.

Korzystając z twierdzenia Pitagorasa dla trójkąta $ACF$ mamy

$d^2=a^2+h^2$,

$a^2+h^2=12a^2$,

$h=\sqrt{11}a$.

Możemy wyliczyć długość krawędzi podstawy. Otrzymujemy

$V=\frac{a^2\sqrt{3}}{4}h$,

$\frac{a^2\sqrt{3}}{4}·\sqrt{11}a=\frac{\sqrt{33}}{4}$,

$a^3=1$,

$a=1$.

Wyliczymy teraz długość wysokości graniastosłupa $h=\sqrt{11}a=\sqrt{11}$. Możemy obliczyć pole powierzchni całkowitej naszego graniastosłupa

$P_{pc}=\frac{a^2\sqrt{3}}{2}+3ah=\frac{\sqrt{3}}{2}+3\cdot 1\cdot \sqrt{11}=\frac{\sqrt{3}}{2}+3\sqrt{11}$.

W graniastosłupie prawidłowym trójkątnym $ABCDEF$ poprowadzono płaszczyznę $\pi$ przechodzącą przez wysokość dolnej podstawy $AP$, gdzie $P$ jest spodkiem wysokości i wierzchołek $F$ górnej podstawy, tak, że płaszczyzna $\pi$ tworzy z płaszczyzną podstawy kąt którego tangens jest równy $2\sqrt{3}$. Pole przekroju graniastosłupa wyznaczonego przez płaszczyznę $\pi$ jest równe $8\sqrt{39}$. Obliczymy pole powierzchni całkowitej tego graniastosłupa.

Rozwiązanie:

RS5XfzqfOVUv4

Ilustracja przedstawia graniastosłup o podstawie trójkąta. Wierzchołki dolnej podstawy to A B oraz C, a wierzchołki górnej podstawy podpisano D E F. Na krawędzi BC zaznaczono punkt P. W graniastosłupie zaznaczono trójkąt prostokątny APF. Kąt APF to kąt prosty, kąt FPC podpisano literą alfa.

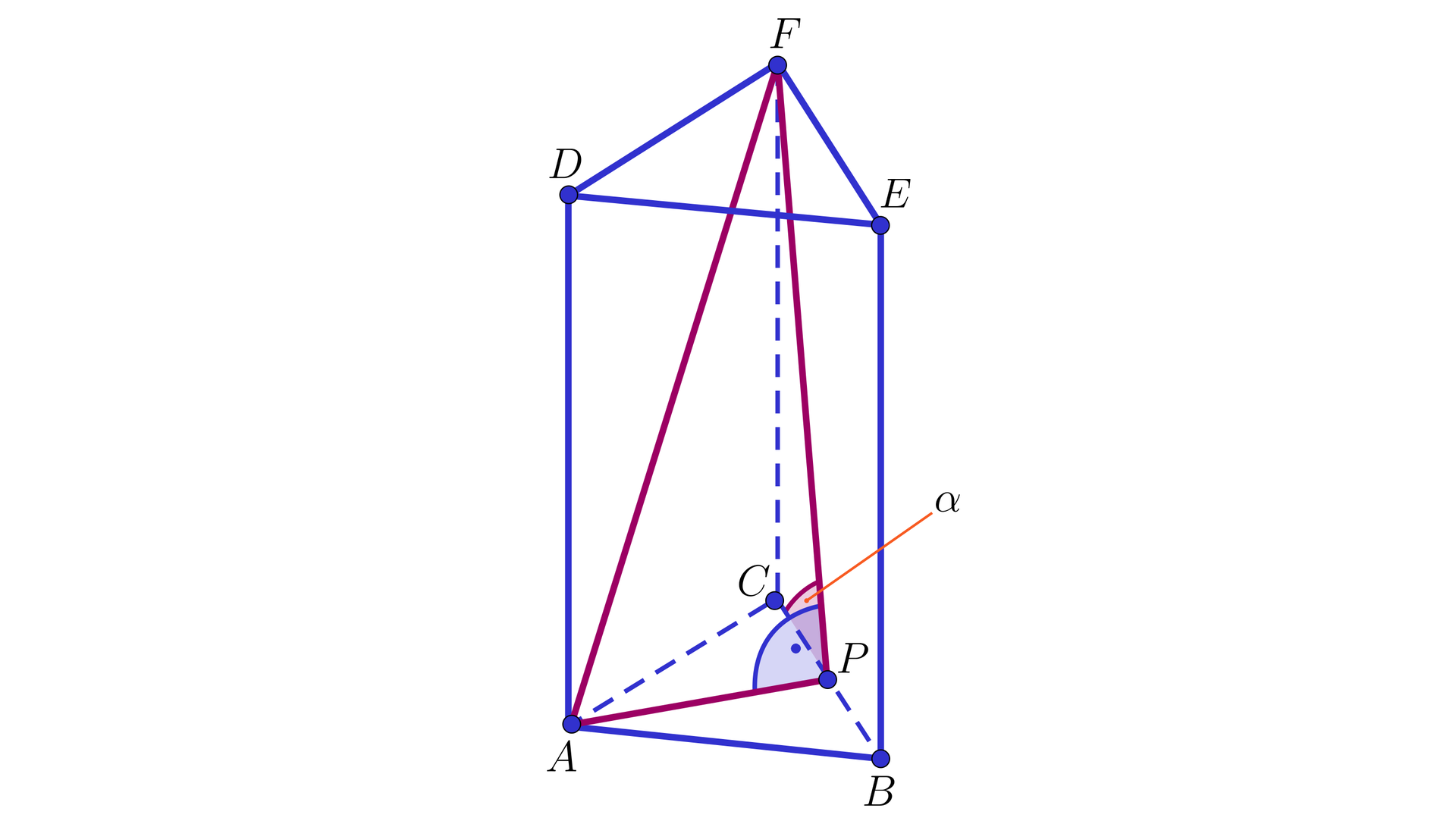
Niech $a>0$ oznacza długość krawędzi podstawy, $h>0$ długość wysokości oraz $d>0$ długość przekątnej ściany bocznej rozważanego graniastosłupa. Trójkąt prostokątny $APF$ jest przekrojem graniastosłupa wyznaczonym przez płaszczyznę $\pi$ o przyprostokątnych $\left|AP\right|=\frac{a\sqrt{3}}{2}$ oraz $\left|PF\right|=\sqrt{h^2+\frac{1}{4}{a}^2}$. Z warunków zadania mamy

$\mathrm{tg}\alpha =\frac{\left|CF\right|}{\left|CP\right|}$,

$\frac{h}{{\displaystyle \frac{a}{2}}}=2\sqrt{3}$,

$h=\sqrt{3}a$.

Wiemy ponadto, że

$\frac{1}{2}·\frac{a\sqrt{3}}{2}·\sqrt{h^2+\frac{1}{4}{a}^2}=8\sqrt{39}$.

Otrzymujemy kolejno

$\frac{a\sqrt{3}}{4}\sqrt{3a^2+\frac{1}{4}{a}^2}=8\sqrt{39}$

$\frac{a\sqrt{3}}{4}·\frac{a\sqrt{13}}{2}=8\sqrt{39}$,

$\frac{a^2\sqrt{39}}{8}=8\sqrt{39}$,

$a=8$.

Wyliczymy teraz długość wysokości graniastosłupa $h=\sqrt{3}a=8\sqrt{3}$. Możemy obliczyć pole powierzchni całkowitej naszego graniastosłupa

$P_{pc}=\frac{a^2\sqrt{3}}{2}+3ah=\frac{8^2·\sqrt{3}}{2}+3·8·8\sqrt{3}=224\sqrt{3}$.

graniastosłup prosty, którego podstawą jest trójkąt równoboczny

przedstawienie graniastosłupa na płaszczyźnie, powstające poprzez “rozcięcie” niektórych jego krawędzi tak, aby dało się rozłożyć ściany na płaszczyźnie

w dowolnym trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej tego trójkąta