Algorytmy liczbowe

Na lekcjach matematyki możesz się spotkać z różnymi zadaniami, w których należy kilkakrotnie wykonać określone działania. Rozwiązania takich problemów najlepiej zapisać za pomocą algorytmów iteracyjnych. Dzięki wykorzystaniu instrukcji iteracyjnych otrzymujemy krótki, zrozumiały algorytm, który po implementacji w danym języku programowania może zostać wykonany przez komputer. Rozważmy problem obliczania średniej arytmetycznejśrednia arytmetycznaśredniej arytmetycznej.

Wyobraź sobie, że chcesz obliczyć średnią arytmetyczną swoich ocen na świadectwie ukończenia szkoły. Aby rozwiązać to zadanie, musisz wykonać następujące działanie:

gdzie $n$ jest liczbą twoich ocen, natomiast $a_1$, $a_2$, $\dots$, $a_n$ to wartości ocen. Zatem średnia arytmetyczna jest sumą liczb podzieloną przez ich liczbę.

Naszym celem jest obliczenie średniej arytmetycznej. Zaczniemy od pobrania od użytkownika liczby n (czyli liczby wszystkich ocen, których średnią będziemy obliczać), a następnie na podstawie tej wiadomości wykonamy n iteracjiiteracjaiteracji pętli, w których będziemy kolejno dodawać pobierane liczby do sumy, zgodnie ze wzorem na średnią. Na końcu obliczymy iloraz otrzymanej sumy przez liczbę n.

Zapiszmy rozwiązanie problemu w postaci schematu blokowego. Zaczniemy od wczytania liczby n.

RGJUDND8wVKau

Ilustracja przedstawia schemat blokowy.
1: Zielony okrąg Start.
2: Fioletowy równoległobok Wczytaj n.

Następnie zmiennej suma nadajemy wartość początkową $0$. Do niej będziemy dodawać kolejne wartości ocen. Utworzymy także zmienną licznikliczniklicznik, której nadamy wartość $1$. Licznik to bardzo ważna zmienna używana w algorytmach iteracyjnych. Dzięki niej możemy kontrolować zachowanie pętli, zawiera ona bowiem wartość określającą liczbę wykonanych iteracji pętli, czyli wskazuje, ile razy zostały powtórzone określone instrukcje. Z każdą kolejną iteracją wartość zmiennej licznik jest zwiększana o $1$. W naszym przypadku rozpoczynamy od iteracji pierwszej, a skończymy na iteracji n-tej.

RwzTrqYTt4ays

Ilustracja przedstawia schemat blokowy.
1 Zielony okrąg Start.
2 Fioletowy równoległobok Wczytaj n.
3 Błękitny prostokąt suma := 0, licznik := 1.

Kolejnym krokiem jest sprawdzenie, czy nasz licznik jest mniejszy lub równy n, a więc czy wykonano już n iteracji pętli (czy zostało pobranych i dodanych już do siebie n liczb). Jeżeli warunek ten jest spełniony, to znaczy, że pozostała nam do dodania co najmniej jedna liczba. Pobieramy ją zatem od użytkownika, a następnie dodajemy ją do zmiennej suma i zwiększamy licznik o $1$, aby zapisać, że kolejna iteracja została wykonana. Wtedy ponownie wracamy do sprawdzenia warunku, zgodnie z definicją pętli.

RzFTRExowwd4A

Ilustracja przedstawia schemat blokowy.
1 Zielony okrąg Start.
2 Fioletowy równoległobok Wczytaj n.
3 Błękitny prostokąt suma := 0, licznik := 1.
4 Niebieski romb licznik mniejszy równy n.
Dla nie w kroku 4,
5 Strzałka wychodząca poza schemat.
Dla tak w kroku 4,
5 Fioletowy równoległobok Wczytaj a.
6 Błękitny prostokąt suma := suma+a, licznik := licznik +1.
7 Powrót do kroku 4.

Jeżeli warunek nie jest spełniony (czyli licznik osiągnął wartość większą od n), to znaczy, że zostało wykonanych już n iteracji pętli. Możemy wtedy podzielić obliczoną sumę wszystkich liczb przez ich liczbę, zgodnie ze wzorem na średnią arytmetyczną. Po tej operacji wypisujemy średnią i kończymy algorytm.

R13dP5cvHctpl

Ilustracja przedstawia schemat blokowy.
1 Zielony okrąg Start.
2 Fioletowy równoległobok Wczytaj n.
3 Błękitny prostokąt suma := 0, licznik := 1.
4 Niebieski romb licznik mniejszy równy n.
Dla nie w kroku 4,
5 Błękitny prostokąt średnia := suma podziel przez n.
6 Fioletowy równoległobok Wypisz średnia.
7 Czerwony okrąg Stop.
Dla tak w kroku 4,
5 Fioletowy równoległobok Wczytaj a.
6 Błękitny prostokąt suma := suma+a, licznik := licznik +1.
7 Powrót do kroku 4.

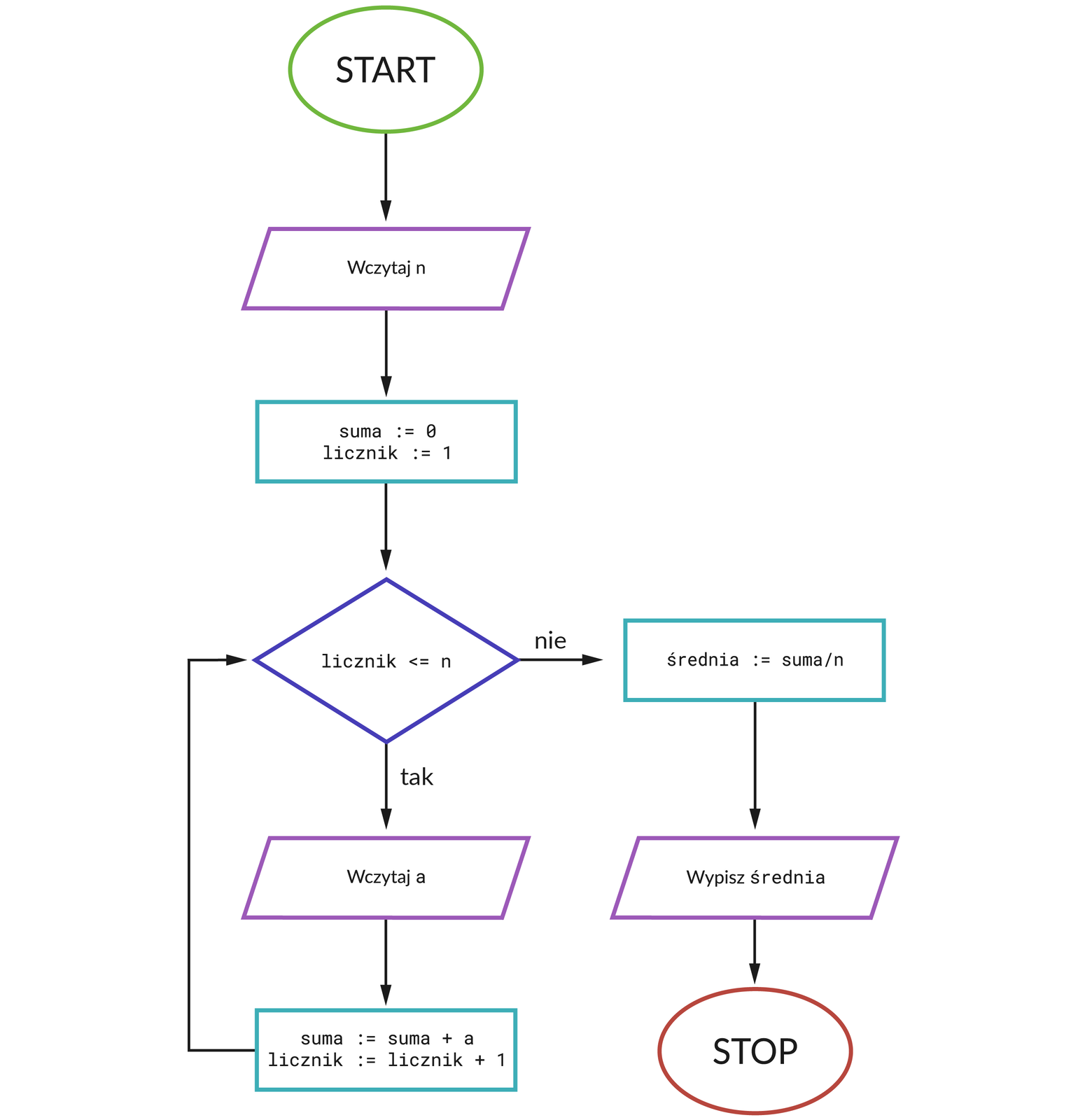
Schemat blokowy przedstawia kompletny algorytm obliczania średniej arytmetycznej n liczb podanych przez użytkownika. W przypadku naszego zadania, w którym musimy obliczyć średnią arytmetyczną wszystkich ocen ze świadectwa ukończenia szkoły, opracowany program:

• pobierze od użytkownika liczbę wszystkich ocen,

• następnie wykona n iteracji wczytujących kolejne oceny i dodających je do zmiennej suma,

• podzieli wartość zmiennej suma przez liczbę wszystkich ocen i wypisze ją na ekran.

Z kolejnych części e‑materiału dowiesz się, w jaki sposób analogicznie opracować schemat blokowy i pseudokod algorytmu obliczającego średnią geometryczną, a następnie wykonasz samodzielnie kilka zadań związanych z tworzeniem algorytmów liczbowych.

Słownik