Przeczytaj
Asymptoty wykresów funkcji pozwalają lepiej wyobrazić sobie ich kształt. Asymptoty nie są częścią wykresu, stanowią jedynie linie pomocnicze przy szkicowaniu wykresów.
Są trzy rodzaje asymptot:
pionowe,
poziome,
ukośne.
W poniższym materiale omówimy asymptoty ukośne.
Asymptota ukośna lewostronna wykresu funkcjiAsymptota ukośna lewostronna wykresu funkcji
Niech funkcja będzie określona w przedziale , gdzie .
Prosta jest asymptotą ukośną lewostronną wykresu funkcji , jeżeli granica różnicy wartości funkcji i funkcji liniowej dla dążącego do jest równa zero:
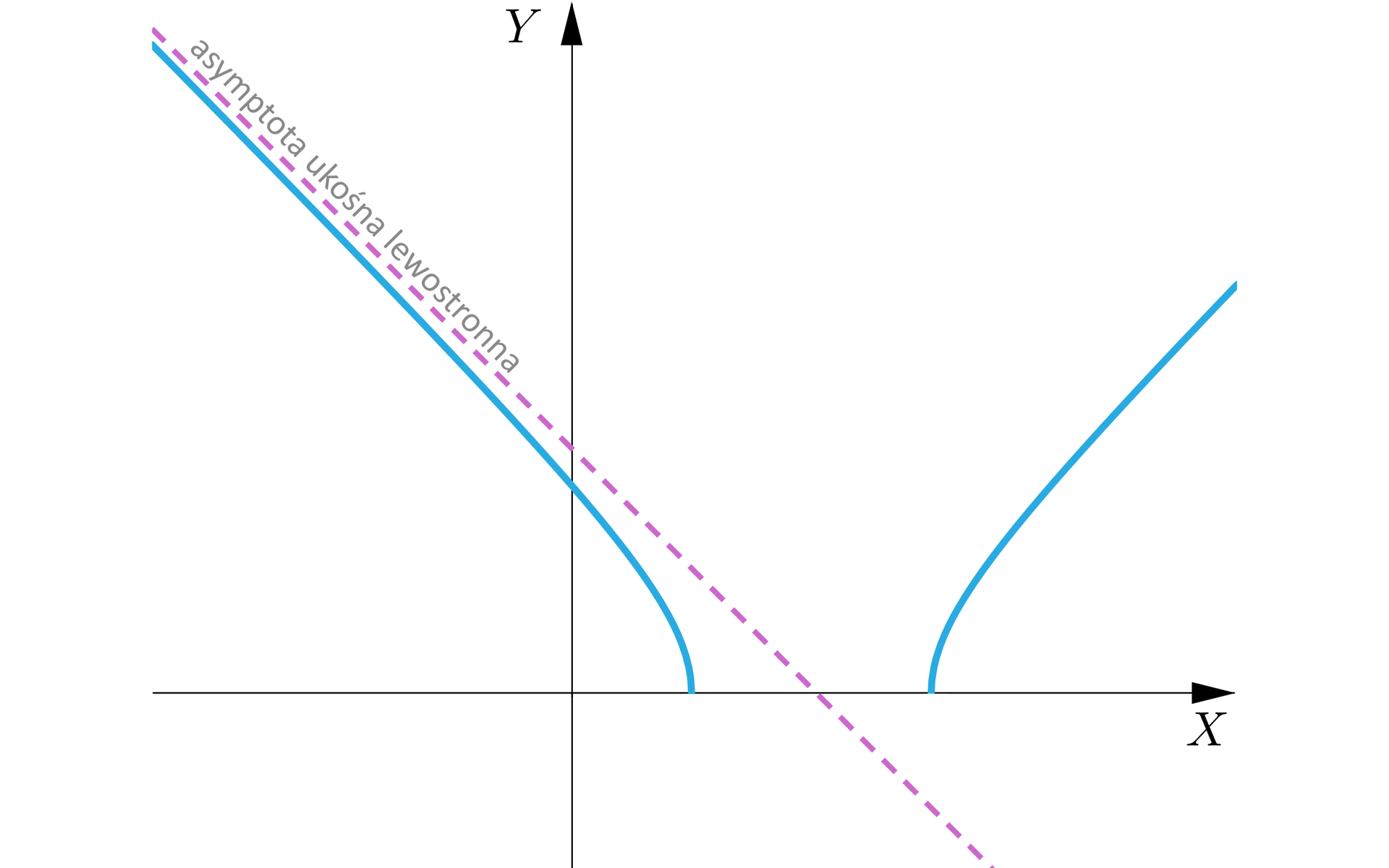
Z definicji asymptoty ukośnej lewostronnej wynika, że wykres funkcji dla dążącego do coraz bardziej zbliża się do asymptoty.
Prosta jest asymptotą lewostronną ukośną wtedy i tylko wtedy, gdy
i granice te są właściwe.
Asymptota ukośna prawostronna wykresu funkcjiAsymptota ukośna prawostronna wykresu funkcji
Niech funkcja będzie określona w przedziale , gdzie .
Prosta jest asymptotą ukośną prawostronną wykresu funkcji , jeżeli granica różnicy wartości funkcji i funkcji liniowej dla dążącego do jest równa zero:

Z definicji asymptoty ukośnej prawostronnej wynika, że wykres funkcji wraz ze wzrostem argumentów coraz bardziej zbliża się do asymptoty.
Prosta jest asymptotą prawostronną ukośną wtedy i tylko wtedy, gdy
i granice te są właściwe.
Jeżeli prosta jest asymptotą ukośną prawostronną krzywej o równaniu , to zgodnie z definicją asymptoty ukośnej mamy:
, zatem: .
Wyrażenie: zapisujemy następująco: .
Ponieważ , to, korzystając z twierdzenia o granicy sumy dwóch granic, z których każda ma granicę właściwą, otrzymujemy:
.
Aby otrzymać drugą z granic, skorzystamy z równości oraz z twierdzenia o granicy sumy funkcji:
, więc , czyli .
Z udowodnionego twierdzenia wynika, że istnienie granic właściwych oraz jest warunkiem koniecznym i wystarczającym na to, aby prosta była asymptotą ukośną prawostronną krzywej .
Podobnie można udowodnić, że istnienie granic właściwych oraz jest warunkiem koniecznym i wystarczającym na to, aby prosta była asymptotą ukośną lewostronną krzywej .
Jeżeli prosta jest jednocześnie asymptotą ukośną prawostronną i lewostronną, to nazywamy ją asymptotą obustronną wykresu funkcji .
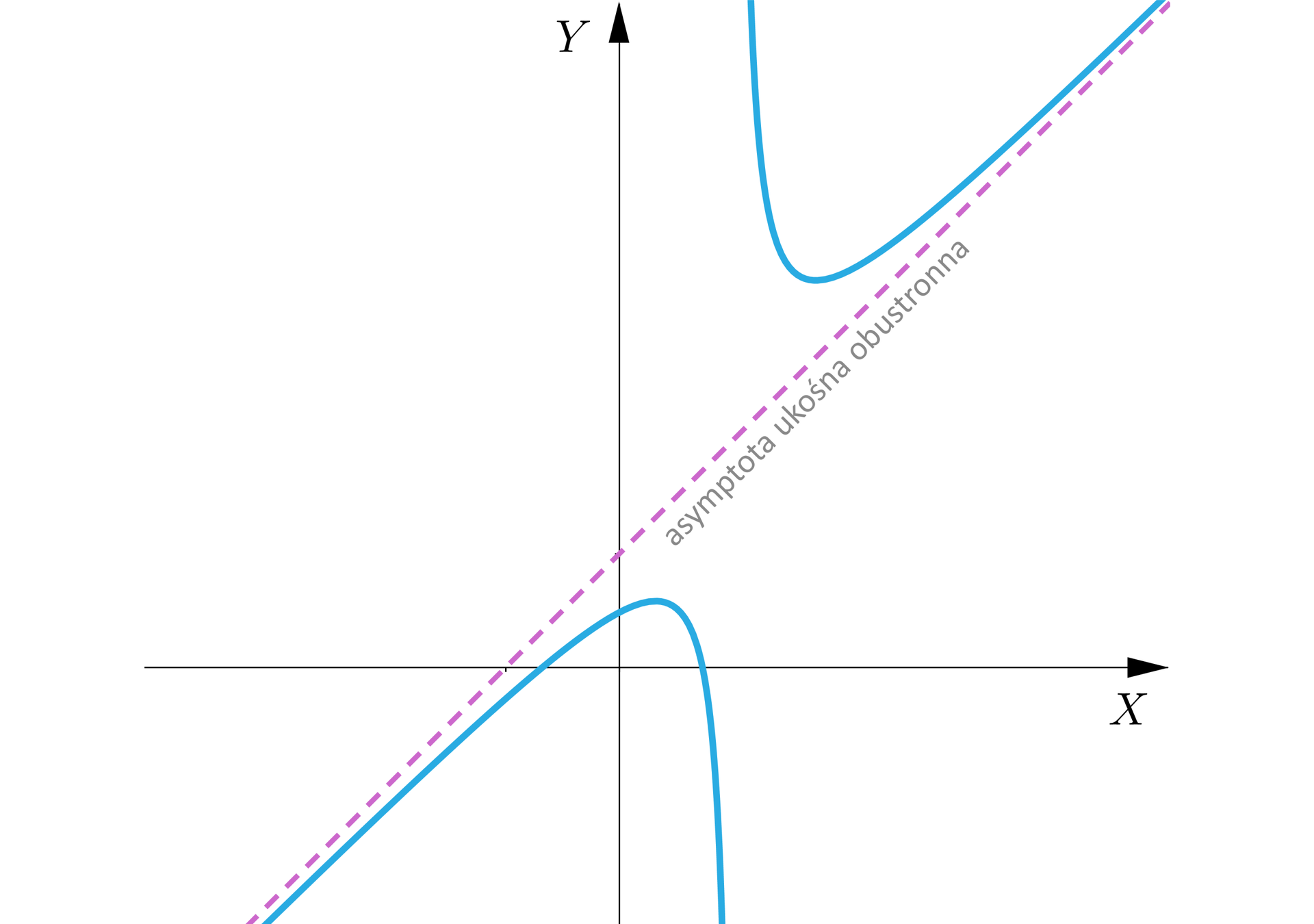
Jeżeli współczynnik kierunkowy asymptoty ukośnej wynosi zero, to asymptotę ukośną nazywamy asymptotą poziomą.
Asymptota pozioma jest szczególnym przypadkiem asymptoty ukośnej, dlatego też jeśli istnieje asymptota pozioma lewostronna lub prawostronna, to nie badamy istnienia asymptoty ukośnej.
Jeżeli funkcja daje się przedstawić w postaci , przy czym spełniony jest warunek:
, to prosta jest asymptotą ukośną lewostronną krzywej .
Jeżeli funkcja daje się przedstawić w postaci , przy czym spełniony jest warunek:
, to prosta jest asymptotą ukośną prawostronną krzywej .
Sprawdzimy, czy prosta o równaniu: jest asymptotą ukośną obustronną wykresu funkcji .
Rozwiązanie
Sprawdzamy, czy prosta jest asymptotą ukośną lewostronną wykresu funkcji :
Sprawdzamy teraz, czy prosta jest asymptotą ukośną prawostronną wykresu funkcji :
Zatem prosta o równaniu jest asymptotą ukośną obustronną wykresu funkcji
Wyznaczymy równanie asymptoty ukośnej lewostronnej wykresu funkcji .
Rozwiązanie
Wyznaczamy współczynnik kierunkowy asymptoty ze wzoru:
Wyznaczamy współczynnik ze wzoru:
Zatem równanie asymptoty ukośnej lewostronnej wykresu funkcji ma postać:
Wyznaczymy równanie asymptoty ukośnej prawostronnej wykresu funkcji .
Rozwiązanie
Wyznaczamy współczynnik kierunkowy asymptoty ze wzoru:
Wyznaczamy współczynnik ze wzoru:
Zatem równanie asymptoty ukośnej prawostronnej wykresu funkcji ma postać:
Wyznaczymy równania asymptot ukośnych wykresu funkcji .
Rozwiązanie
Równania asymptot ukośnych wyznaczymy na dwa sposoby.
Sposób 1
Funkcja jest określona, gdy , więc dziedziną tej funkcji jest zbiór .
Prosta jest asymptotą lewostronną ukośną wtedy i tylko wtedy, gdy
oraz i granice te są właściwe.
Obliczamy granice:
.
Zatem:
.
Mamy teraz: .
Ponieważ
,
to .
Prosta o równaniu jest asymptotą ukośną lewostronną wykresu funkcji .
Analogicznie wyznaczamy równanie asymptoty ukośnej prawostronnej:
.
Prosta o równaniu jest asymptotą ukośną prawostronną wykresu funkcji .
Odpowiedź
Prosta o równaniu jest asymptotą ukośną obustronną wykresu funkcji .
Sposób 2
Rozwiążemy teraz ten przykład korzystając z twierdzenia o wyznaczaniu asymptot ukośnych.
Ponieważ licznik funkcji jest stopnia wyższego niż mianownik, dzielimy licznik przez mianownik:
Możemy więc funkcję zapisać w postaci , czyli
.
Oznaczmy przez i zauważmy, że , więc prosta jest asymptotą ukośną prawostronną wykresu funkcji .
Podobnie pokazujemy, że prosta jest asymptotą ukośną lewostronną wykresu tej funkcji.
Odpowiedź
Prosta jest asymptotą ukośną obustronną wykresu funkcji .
Wyznaczymy równania asymptot wykresu funkcji .
Rozwiązanie
Funkcja jest określona dla , zatem: .
Zauważmy, że oraz , więc prosta jest asymptotą pionową wykresu funkcji .
Ponieważ licznik funkcji jest stopnia wyższego niż mianownik, dzielimy licznik przez mianownik:
Funkcję zapisujemy w postaci .
Prosta jest asymptotą ukośną obustronną wykresu funkcji ponieważ i .
Słownik
prosta jest asymptotą ukośną lewostronną wykresu funkcji , jeżeli granica różnicy wartości funkcji i funkcji liniowej dla jest równa zero
prosta jest asymptotą ukośną prawostronną wykresu funkcji , jeżeli granica różnicy wartości funkcji i funkcji liniowej dla jest równa zero