Przeczytaj
Przypomnijmy najpierw podstawowe pojęcie.
Kątem między odcinkami nazywamy kąt między prostymi zawierającymi te odcinki.
Kąty rozważane w graniastosłupie zwykle zawarte są między odcinkami o wspólnym początku.
Spośród odcinków w graniastosłupie warto szczególnie zwrócić uwagę na przekątne ścian, przekątne graniastosłupa, krawędzie graniastosłupa, wysokości ścian oraz graniastosłupa.
Graniastosłup trójkątny
Na poniższych rysunkach zaznaczono kilka najczęściej rozważanych kątów między odcinkami graniastosłupa trójkątnego.
Ilustracja pierwsza przedstawia graniastosłup prawidłowy trójkątny A B C D E F. Zaznaczono na nim kąt FAB między krawędzią boczną a krawędzią podstawy.
Ilustracja druga przedstawia graniastosłup prawidłowy trójkątny A B C D E F. Zaznaczono na nim kąt FAG między krawędzią boczną a wysokością podstawy.
Ilustracja trzecia przedstawia graniastosłup prawidłowy trójkątny A B C D E F. Zaznaczono na nim kąt AFB między krawędzią boczną a przekątną ściany bocznej.
Ilustracja czwarta przedstawia graniastosłup prawidłowy trójkątny A B C D E F. Zaznaczono na nim kąt ABF między przekątną ściany bocznej graniastosłupa a krawędzią podstawy.
Zwróćmy jeszcze uwagę, że w niektórych graniastosłupach pewne odcinki pokrywają się, zaś w innych są zupełnie różne. Dobrym przykładem jest krawędź boczna i wysokość graniastosłupa, które pokrywają się w graniastosłupach prostych, ale są różnymi odcinkami w graniastosłupach pochyłych. Poniżej galeria kątów między odcinkami w graniastosłupie trójkątnym pochyłym. Porównaj je z kątami zaznaczonymi wyżej między odcinkami w graniastosłupie trójkątnym prostym.
Ilustracja pierwsza przedstawia graniastosłup pochyły AB C D E F o podstawie trójkąta. Zaznaczono na nim kąt AFG między wysokością graniastosłupa, a jego krawędzią boczną.
Ilustracja druga przedstawia graniastosłup pochyły AB C D E F o podstawie trójkąta. Zaznaczono na nim kąt FAB między krawędzią boczną, a krawędzią podstawy graniastosłupa.
Ilustracja trzecia przedstawia graniastosłup pochyły AB C D E F o podstawie trójkąta. Zaznaczono na nim kąt ABF między przekątną ściany bocznej, a krawędzią podstawy graniastosłupa.
Ilustracja czwarta przedstawia graniastosłup pochyły AB C D E F o podstawie trójkąta. Zaznaczono na nim kąt DBF między przekątną ściany bocznej, a krawędzią boczną graniastosłupa.
Dany jest graniastosłup prawidłowygraniastosłup prawidłowy trójkątny, w którym wysokość podstawy jest równa . Kąt między przekątnymi ścian bocznych wychodzącymi z jednego wierzchołka ma miarę . Obliczymy objętość tego graniastosłupa.
Zacznijmy od wykonania rysunku i zaznaczenia kąta między przekątnymi ścian bocznych.
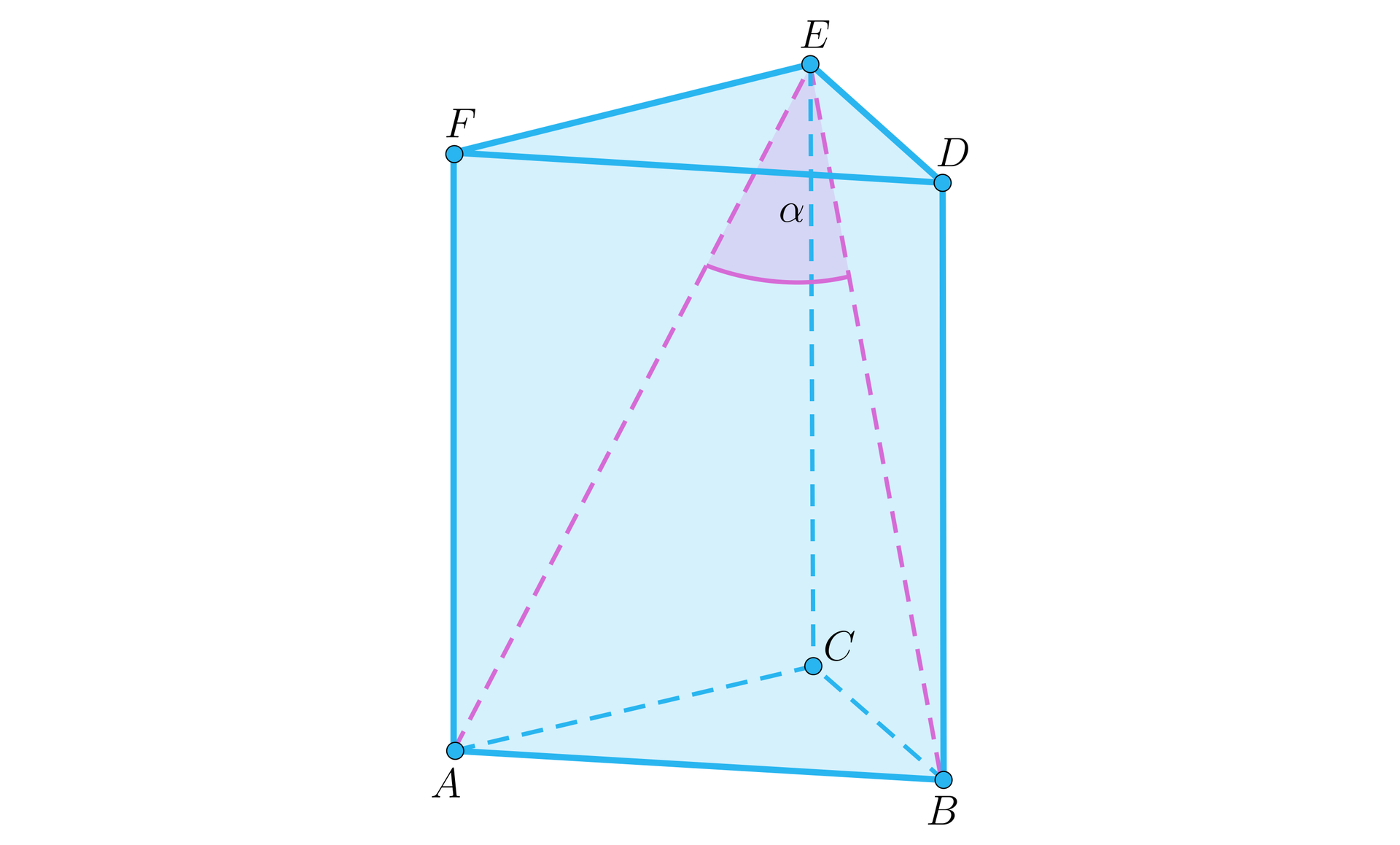
Ponieważ podstawa jest trójkątem równobocznym o wysokości , więc krawędź podstawy ma długość . Zauważmy, że trójkąt jest równoramienny, zatem jego wysokość poprowadzona z wierzchołka pada pod kątem prostym do i zawiera się w dwusiecznej kąta .
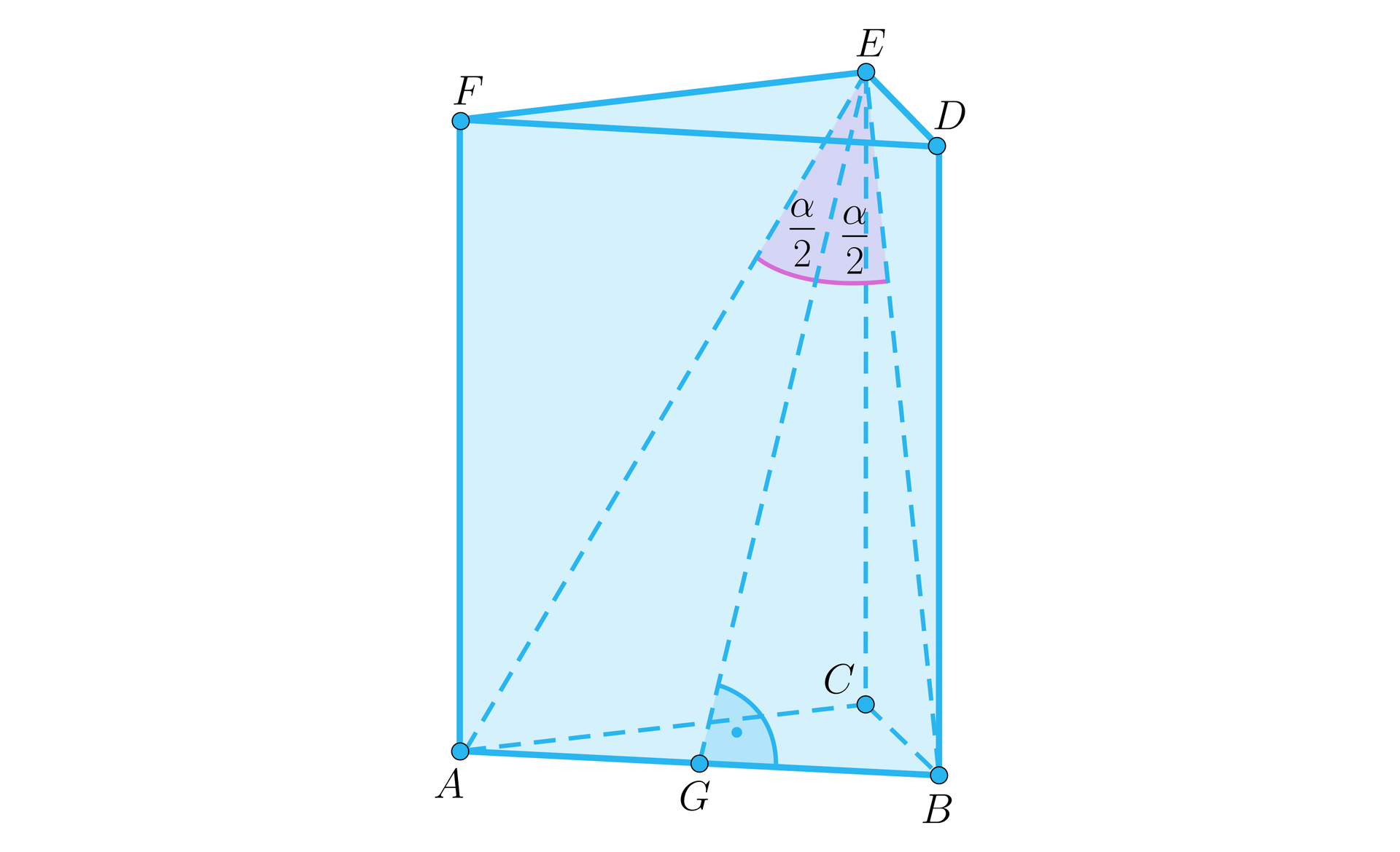
Z funkcji trygonometrycznych w trójkącie mamy , czyli .
Korzystając z tablic trygonometrycznych możemy przybliżyć wartość :
Z twierdzenia Pitagorasa w trójkącie mamy
.
Zatem objętość rozważanego graniastosłupa to
Graniastosłup czworokątny
W graniastosłupie czworokątnym wysokość i krawędź boczna również mogą się pokrywać lub być różnymi odcinkami – w zależności od tego, czy graniastosłup jest prosty, czy pochyły.
Przeanalizuj różnicę między obydwoma graniastosłupami na poniższych rysunkach.
Opis | Graniastosłup prosty | Graniastosłup pochyły |
|---|---|---|
Kąt między wysokością a przekątną ściany bocznej graniastosłupa. | 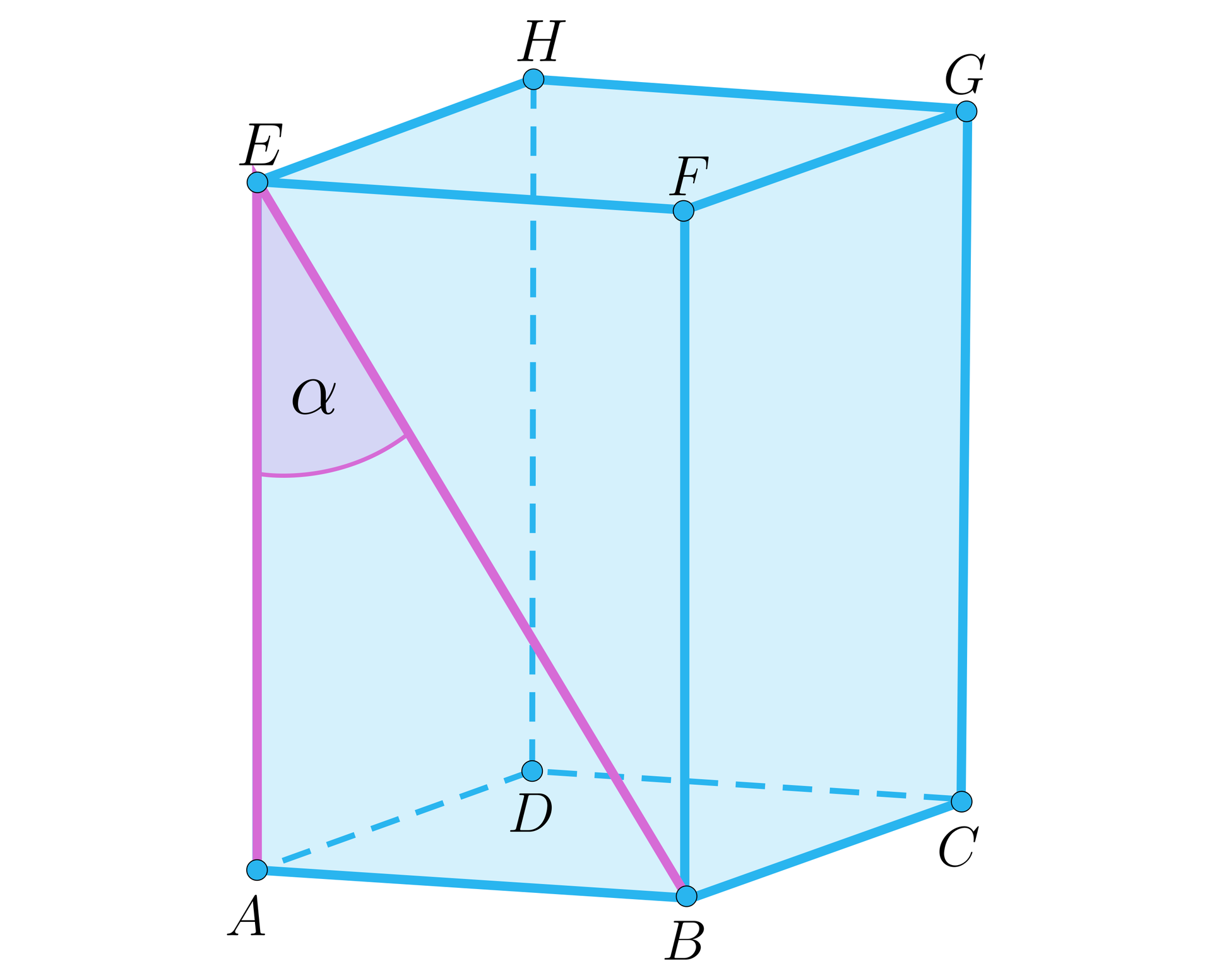 | 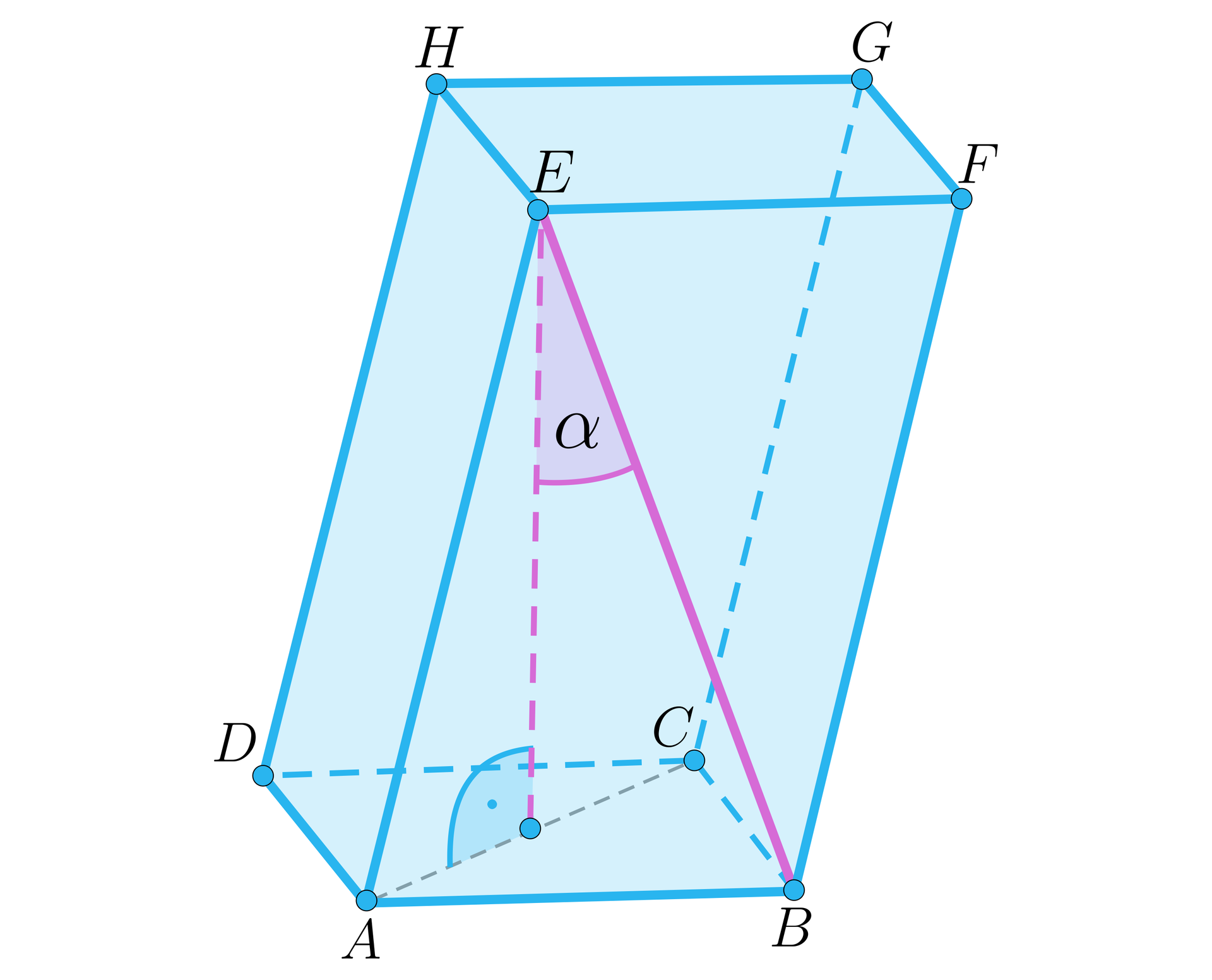 |
Kąt między wysokością a krawędzią boczną graniastosłupa. | 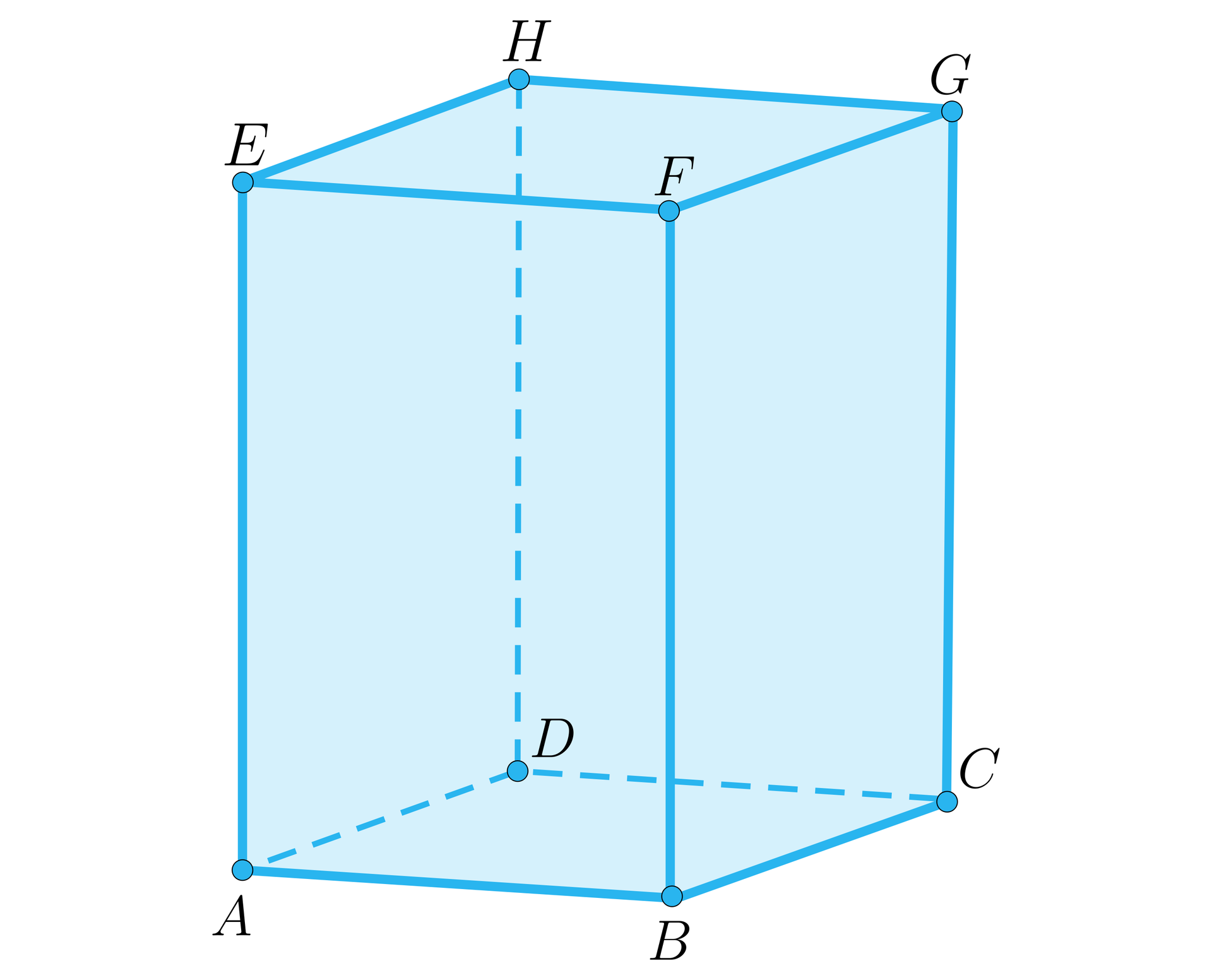 | 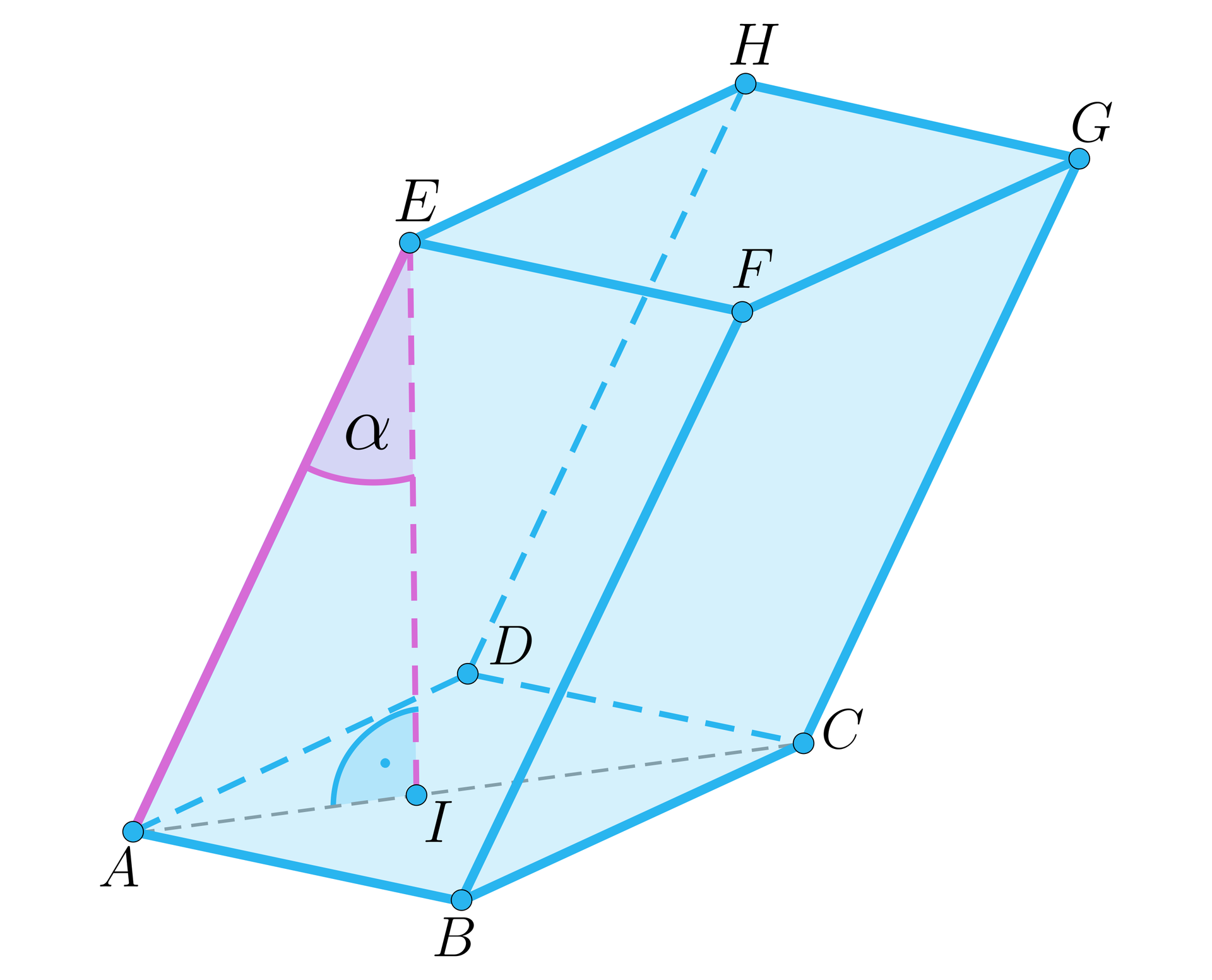 |
Kąt między przekątną ściany bocznej a krawędzią podstawy graniastosłupa. | 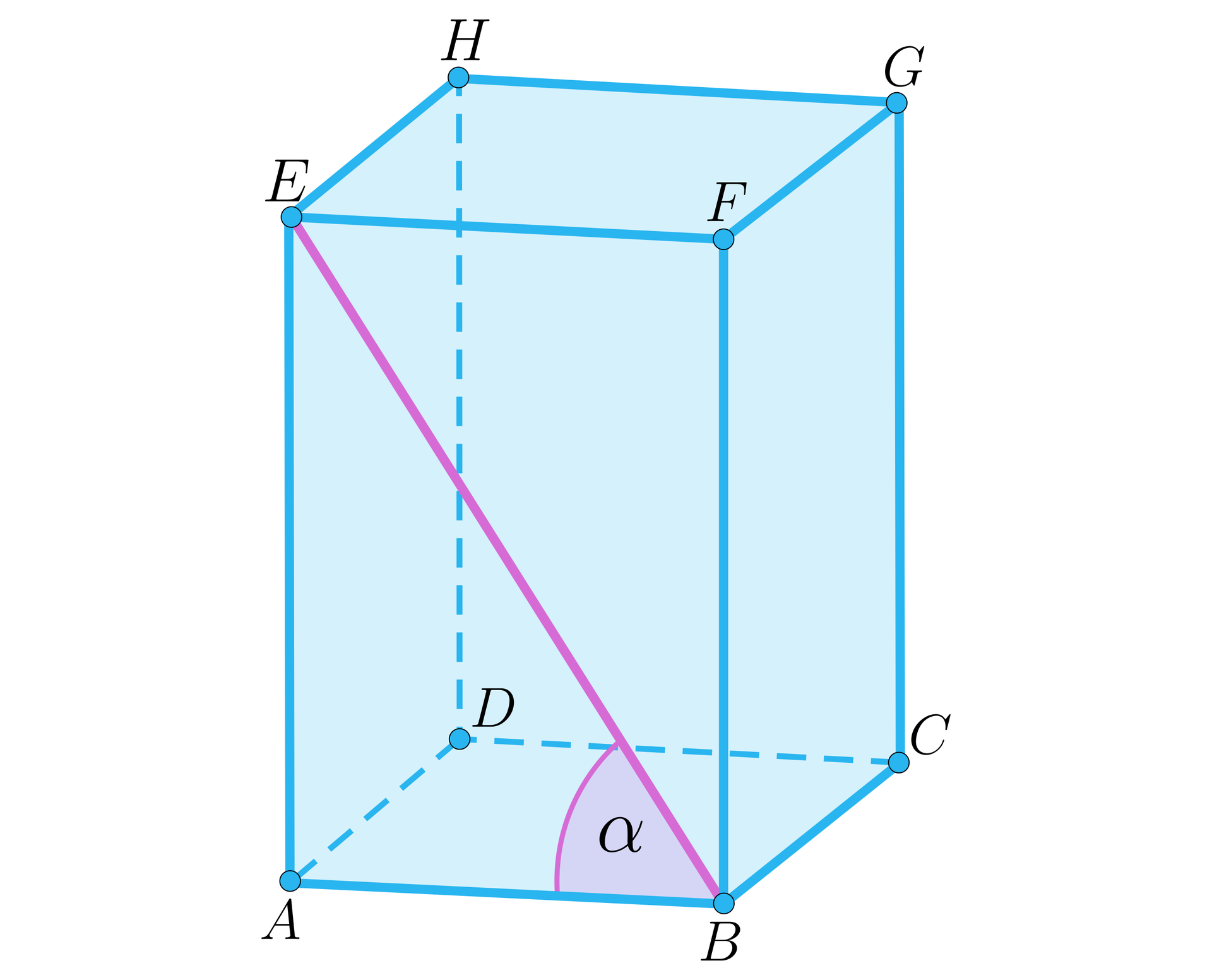 | 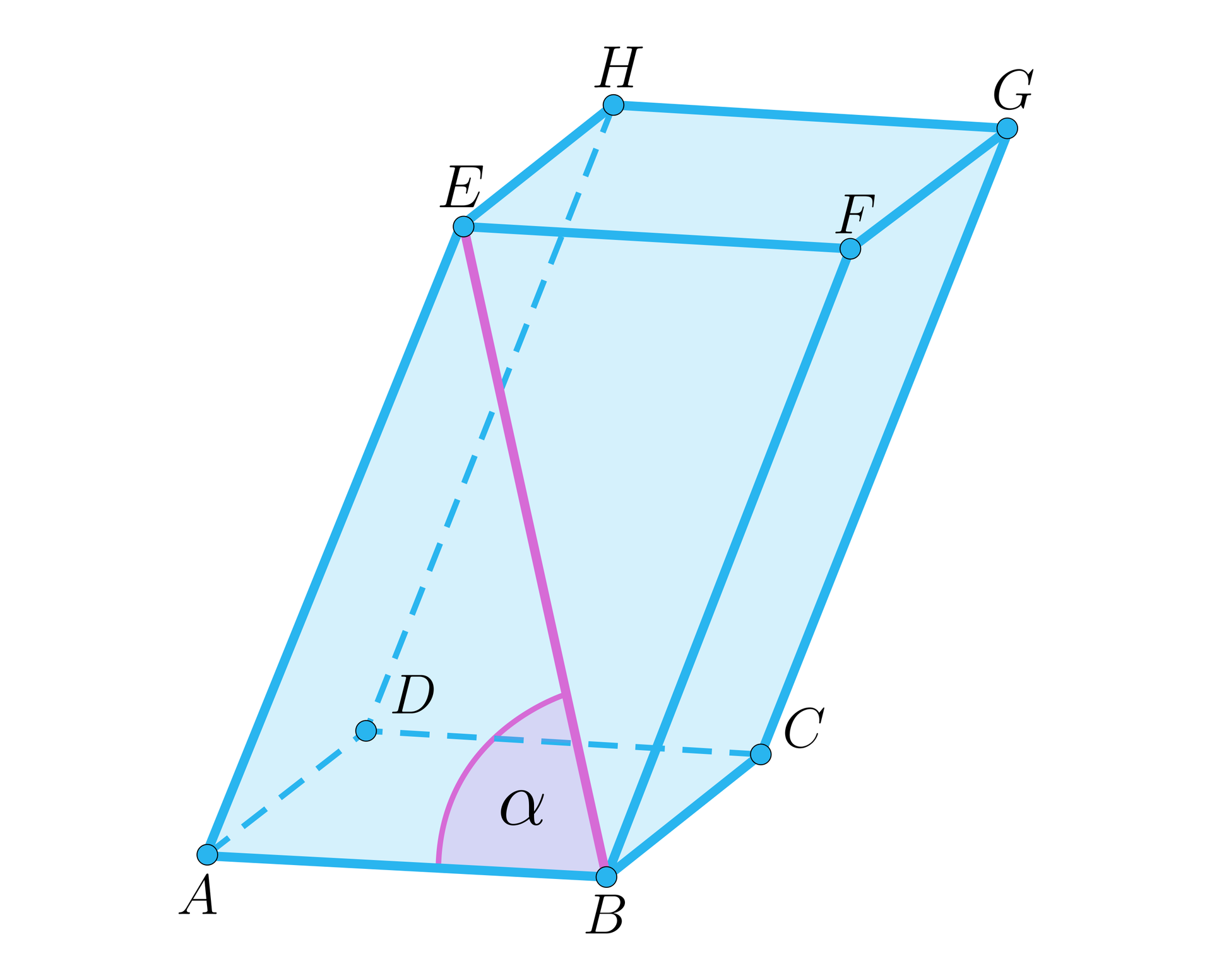 |
Kąt między przekątną graniastosłupa a przekątną ściany bocznej. | 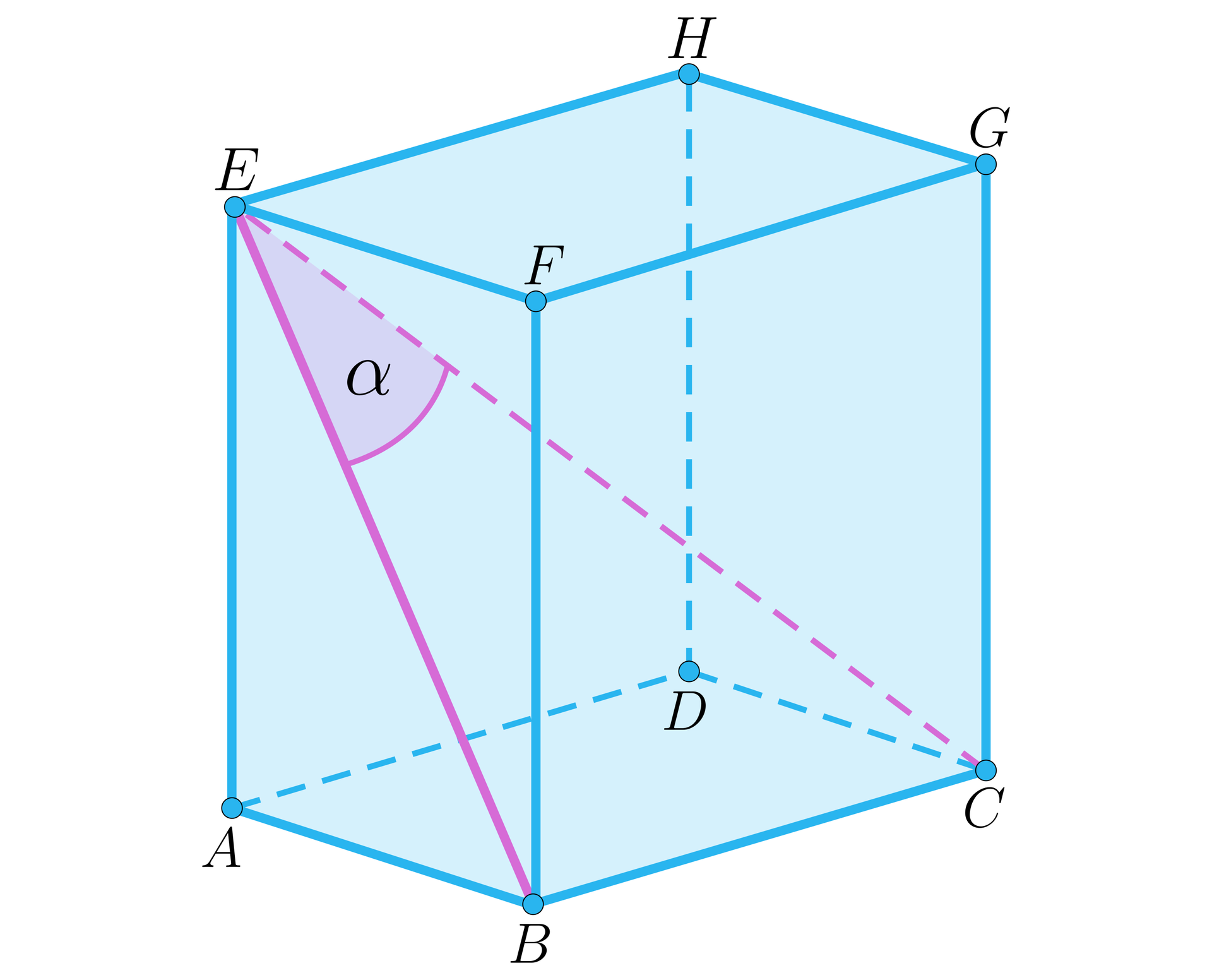 | 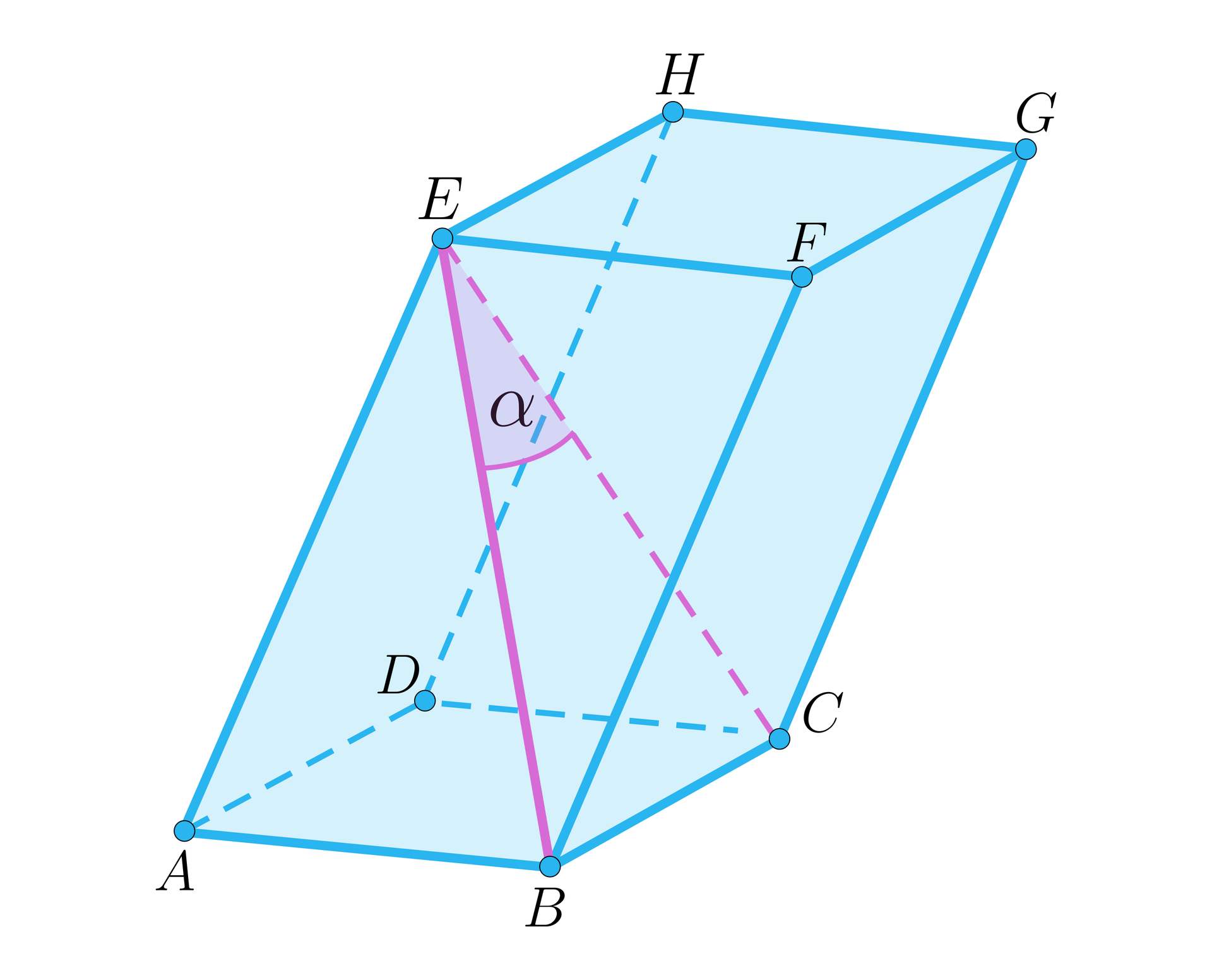 |
Kąt między przekątnymi graniastosłupa. | 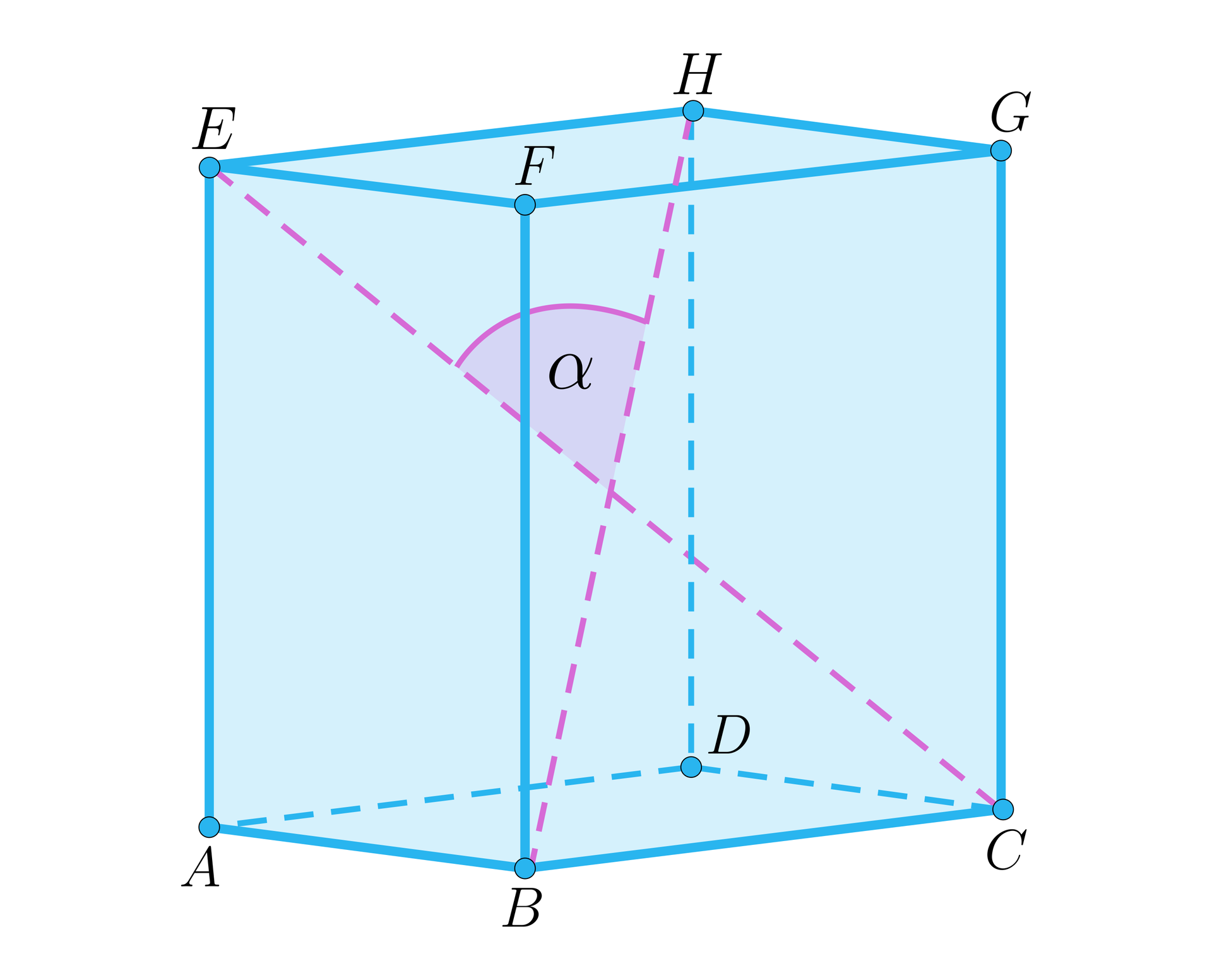 | 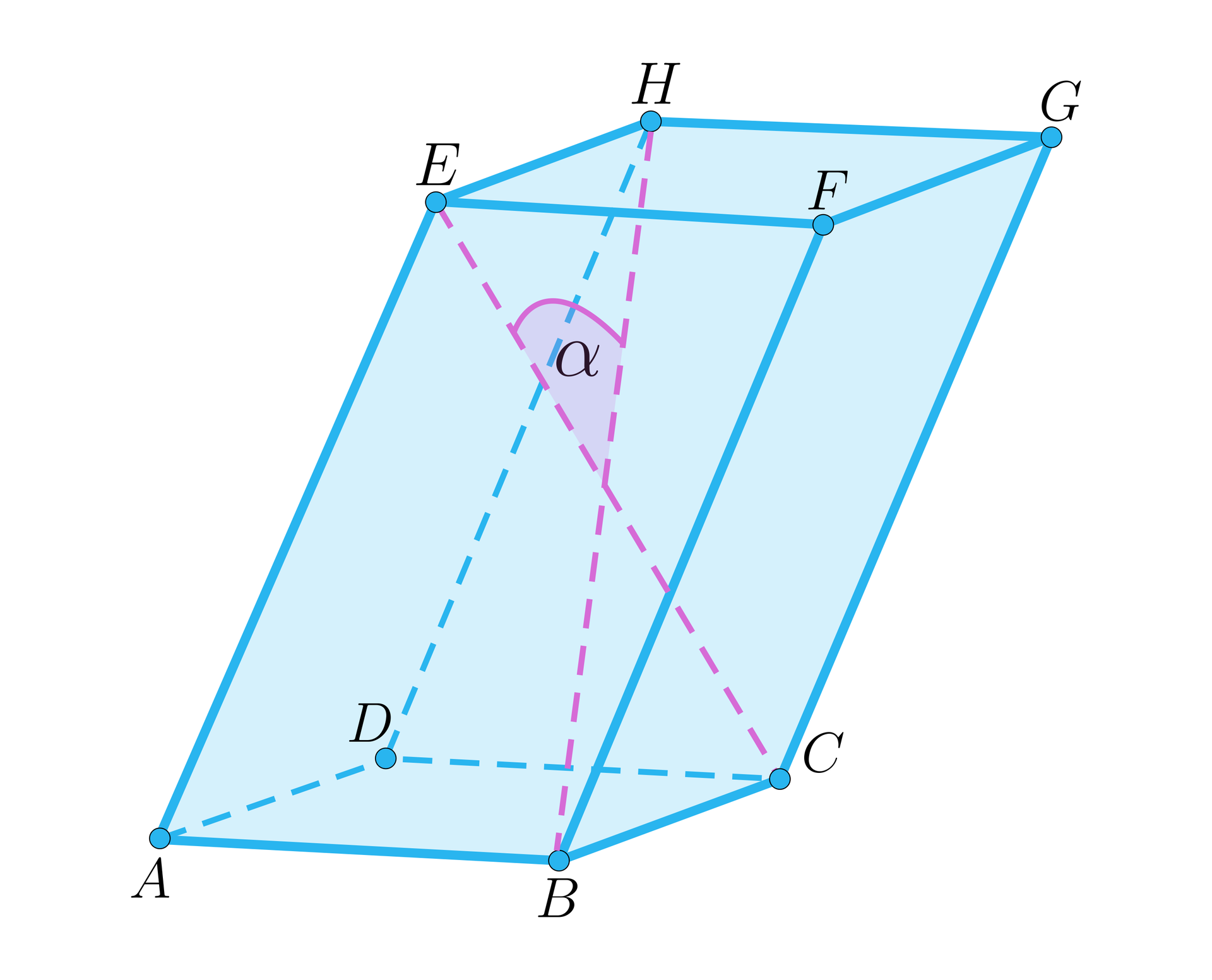 |
Objętość graniastosłupa prawidłowego czworokątnego jest równa . Kąt między przekątną graniastosłupaprzekątną graniastosłupa a przekątną podstawy wychodzącymi z tego samego wierzchołka ma miarę . Obliczymy pole powierzchni całkowitej tego graniastosłupa.
Zaczniemy od rysunku.
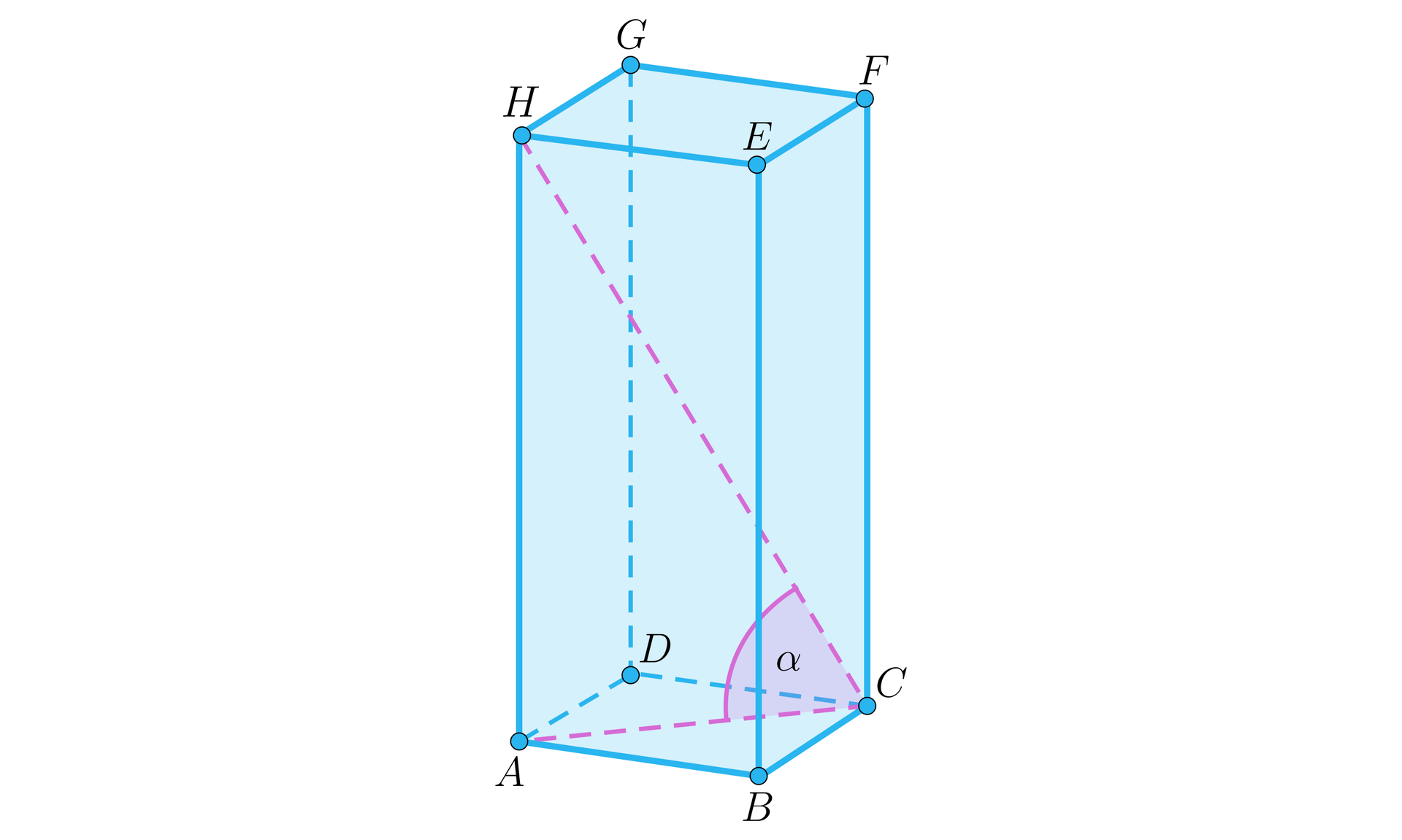
Jeśli przez oznaczymy długość krawędzi podstawy graniastosłupa, to jej przekątna ma długość . Ponieważ trójkąt ma kąty o miarach , , , więc .
Objętość graniastosłupa to iloczyn pola podstawy i wysokości, więc mamy równanie:
Pole powierzchni całkowitej tego graniastosłupa to:
.
Słownik
odcinek łączący dwa wierzchołki graniastosłupa, który nie jest zawarty w żadnym wielokącie tworzącym powierzchnię tego graniastosłupa (nie jest zawarty ani w żadnej ścianie bocznej, ani w żadnej podstawie)
graniastosłup prosty, w którego podstawie znajduje się wielokąt foremny