Przeczytaj

Przeanalizujemy teraz kilka konwencjonalnych problemów, które można rozwiązać z zastosowaniem prawdopodobieństwa klasycznegoklasyczna definicja prawdopodobieństwaprawdopodobieństwa klasycznego. Przypomnimy więc najpierw definicję, z której będziemy korzystać.

Klasyczna definicja prawdopodobieństwa

Definicja: Klasyczna definicja prawdopodobieństwa

Niech $Ω$ będzie skończonym zbiorem wszystkich możliwych zdarzeń elementarnych jednakowo prawdopodobnych.

Prawdopodobieństwem zajścia zdarzenia $A \subset Ω$ nazywamy liczbę:

P (A) = \frac{|A|}{|Ω|}

W zadaniach będziemy zakładać, że wszystkie zdarzenia elementarne są jednakowo prawdopodobne.

Przykład 1

Wśród dziesięciu losów na loterii znajduje się jeden los wygrywający i dwa losy uprawniające do wyciągnięcia następnego losu. Obliczymy, jakie jest prawdopodobieństwo wygranej przy zakupie jednego losu i maksymalnym wykorzystaniu uprawnień?

Oznaczmy:
$A$ – zdarzenie polegające na wygranej przy zakupie jednego losu i maksymalnym wykorzystaniu uprawnień.

Przedstawimy graficznie przebieg doświadczenia.

RACDmNo0dwUk9

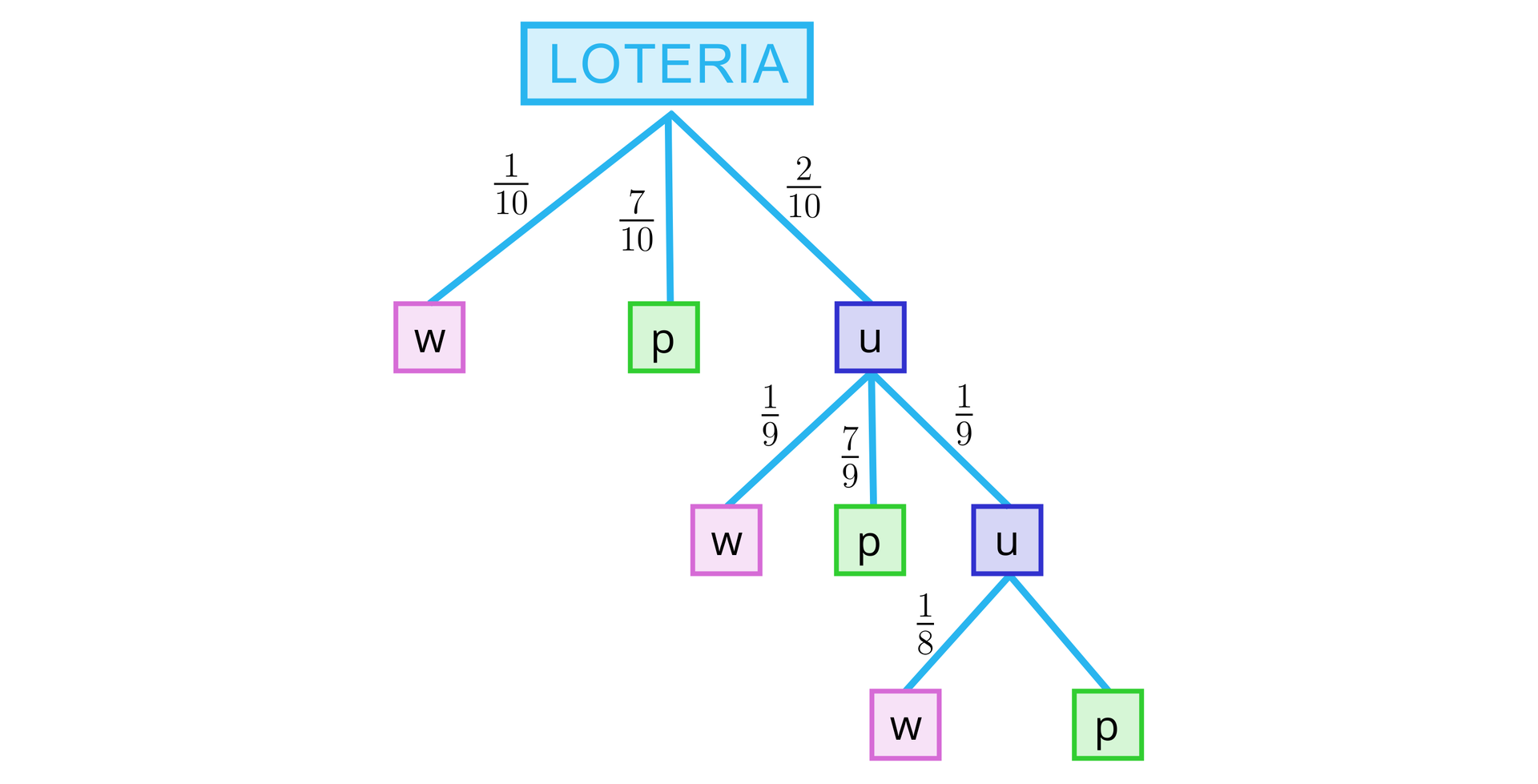
Ilustracja przedstawia drzewko prawdopodobieństwa, jedna dziesiąta szansy na w, siedem dziesiątych szansy na p i dwie dziesiąte szansy na u, przechodzimy rząd niżej wychodząc od u. Jedna dziewiąta szansy na w, siedem dziewiątych szansy na p i jedna dziewiąta szansy na u. Schodzimy rząd niżej wychodząc od u. Jedna ósma szansy na w i nie podana wartość szansy na p.

Z grafu odczytujemy, że mamy trzy możliwości wygranej.

Pierwsza możliwość:

prawdopodobieństwo jest równe $\frac{1}{10}$ (uzyskanie wygranej w pierwszym losowaniu).

Druga możliwość:

prawdopodobieństwo jest równe $\frac{2}{10} \cdot \frac{1}{9} = \frac{2}{90}$ (uzyskanie wygranej w drugim losowaniu).

Trzecia możliwość:

prawdopodobieństwo jest równe $\frac{2}{10} \cdot \frac{1}{9} \cdot \frac{1}{8} = \frac{2}{720}$ (uzyskanie wygranej w trzecim losowaniu).

Prawdopodobieństwo finalne jest równe sumie tych prawdopodobieństw.

$P (A) = \frac{1}{10} + \frac{2}{90} + \frac{2}{720}$

$P (A) = \frac{72}{720} + \frac{16}{720} + \frac{2}{720}$

$P (A) = \frac{90}{720} = \frac{1}{8}$

Odpowiedź:

Prawdopodobieństwo zdarzenia polegającego na wygranej przy zakupie jednego losu i maksymalnym wykorzystaniu uprawnień jest równe $\frac{1}{8}$ .

Przykład 2

RG391TP0cXSvq

Ilustracja przedstawia pięć zawieszonych skarpetek na sznurze. Każda skarpetka ma inny wzór: pierwsza z nich jest w groszki, druga w serduszka, trzecia w zygzaki, czwarta i piąta w falowane linie.

Na sznurze powieszonych jest pięć par skarpetek. Zdejmujemy ze sznura w sposób losowy cztery skarpetki. Oblicz prawdopodobieństwo, że wśród wybranych skarpetek nie ma ani jednej pary.

Pięć par skarpetek, to dziesięć sztuk skarpetek, z których losujemy cztery.

$|Ω| = (\binom{10}{4}) = 210$

Mamy $5$ możliwości wylosowania takich skarpetek, aby nie było wśród nich ani jednej pary.

Wśród wybranych skarpetek są:

cztery skarpetki są z prawej nogi,
jedna skarpetka z lewej nogi trzy z prawej (nie tworzące pary),
dwie skarpetki z lewej nogi, dwie z prawej (nie tworzące pary),
trzy skarpetki z lewej nogi, jedna z prawej (nie tworzące pary),
cztery skarpetki z lewej nogi.

Zatem liczba zdarzeń sprzyjających zdarzeniu: $S$ – wśród wybranych skarpetek nie ma ani jednej pary, jest równa:

$|S| = (\binom{5}{0}) (\binom{5}{4}) + (\binom{5}{1}) (\binom{4}{3}) + (\binom{5}{2}) (\binom{3}{2}) + (\binom{5}{3}) (\binom{2}{1}) + (\binom{5}{4}) (\binom{1}{0})$

$|S| = 5 + 5 \cdot 4 + 5 \cdot 3 \cdot 2 + 5 \cdot 4 \cdot 1 + 5 = 80$

Wyznaczamy szukane prawdopodobieństwo.

$P (A) = \frac{80}{210} = \frac{8}{21}$

Odpowiedź:

Prawdopodobieństwo, że wśród wybranych skarpetek nie ma ani jednej pary jest równe $\frac{8}{21}$ .

Przykład 3

R1Gw3fl4KW3cL1

Ilustracja przedstawia akrobatkę w sukience z odkrytymi ramionami, która wykonuje akrobacje na szarfie przyczepionej do sufitu.

Do finału mistrzostw w akrobatyce cyrkowej zakwalifikowało się $10$ zawodniczek.

Spośród zawodniczek wylosowano trzy, które jako pierwsze mają zaprezentować swoje umiejętności.

Obliczymy prawdopodobieństwo zdarzenia $A$ polegającego na tym, że numer jednej z wylosowanych zawodniczek jest równy sumie numerów dwóch pozostałych zawodniczek.

Zdarzeniami elementarnymi są trzyelementowe podzbiory zbioru $\{1, 2, 3, 4, 5, 6, . . ., 10\}$ .

$|Ω| = (\binom{10}{3}) = 120$

Wyznaczamy zdarzenia sprzyjające zajściu zdarzenia $A$ .

Numer jednej z wylosowanych zawodniczek jest równy sumie numerów dwóch pozostałych zawodniczek, jeżeli suma ta jest równa:

$10 (9 + 1, 8 + 2, 7 + 3, 6 + 4)$ – cztery możliwości,
$9 (8 + 1, 7 + 2, 6 + 3, 5 + 4)$ – cztery możliwości,
$8 (7 + 1, 6 + 2, 5 + 3)$ – trzy możliwości,
$7 (6 + 1, 5 + 2, 4 + 3)$ – trzy możliwości,
$6 (5 + 1, 4 + 2)$ – dwie możliwości,
$5 (4 + 1, 3 + 2)$ – dwie możliwości,
$4 (3 + 1)$ – jedna możliwość,
$3 (2 + 1)$ – jedna możliwość.

Zatem

$| A | = 2 \cdot 4 + 2 \cdot 3 + 2 \cdot 2 + 1 \cdot 2 = 20$

Wyznaczamy prawdopodobieństwo zdarzenia $A$ :

$P (A) = \frac{20}{120} = \frac{1}{6}$

Odpowiedź:

Prawdopodobieństwo zdarzenia polegającego na tym, że numer jednej z wylosowanych zawodniczek jest równy sumie numerów dwóch pozostałych zawodniczek jest równe $\frac{1}{6}$ .

Wiele zadań z rachunku prawdopodobieństwa prowadzi do rozwiązywania nierówności lub równań, w tym kwadratowych. Należy wtedy pamiętać, że uzyskane liczby muszę spełniać warunki zakładane w treści zadania. Z reguły uzyskane liczby powinny być dodatnie i wymierne.

Przykład 4

Niech $k$ będzie liczbą naturalną taką, że $3 < k \leq 20$ . Spośród liczb $1$ , $2$ , $3$ , $. . .$ , $20$ losujemy trzy liczby bez zwracania. Prawdopodobieństwo tego, że największa z wylosowanych liczb jest równa $k$ wynosi $\frac{3}{76}$ . Wyznaczymy liczbę $k$ .

Zdarzeniami elementarnymi są trzywyrazowe podzbiory zbioru dwudziestoelementowego.

Zatem

$|Ω| = (\binom{20}{3}) = \frac{20!}{3! \cdot 17!}$

$|Ω| = \frac{18 \cdot 19 \cdot 20}{6} = 1140$

Oznaczmy:
$A$ – zdarzenie polegające na tym, że największa z wylosowanych liczb jest równa $k$ .

Jeśli największa z wylosowanych liczb jest równa $k$ , to pozostałe dwie liczby są mniejsze od $k$ . Zatem wybieramy je spośród $k - 1$ liczb.

$|A| = (\binom{k - 1}{2}) = \frac{(k - 1)!}{2! \cdot (k - 3)!}$

$|A| = \frac{(k - 1) (k - 2)}{2}$

Z powyższych rozważań wynika, że prawdopodobieństwo zajścia zdarzenia $A$ jest równe

$P (A) = \frac{\frac{(k - 1) (k - 2)}{2}}{1140} = \frac{(k - 1) (k - 2)}{2280}$

Z treści zadania wynika, że prawdopodobieństwo zajścia zdarzenia $A$ jest równe $\frac{3}{76}$ .

Otrzymujemy więc równanie

$\frac{(k - 1) (k - 2)}{2280} = \frac{3}{76}$

Z otrzymanego równania wyznaczamy $k$ .

$\frac{k^{2} - 3 k + 2}{2280} = \frac{3}{76} | \cdot 76$

$k^{2} - 3 k + 2 = 90$

$k^{2} - 3 k - 88 = 0$

$∆ = 361$

$\sqrt{∆} = 19$

$k_{1} = \frac{3 - 19}{2} = - 8 < 0$ – liczba jest ujemna, nie spełnia więc warunków zadania

$k_{2} = \frac{3 + 19}{2} = 11$

Liczba $11$ spełnia warunek zakładany w treści zadania:

$3 < 11 \leq 20$

Odpowiedź:

Liczba $k$ jest równa $11$ .

Przykład 5

Dany jest $2 n + 1$ – kąt foremny ( $n \geq 2$ , $n \in ℕ$ ). Wybieramy w sposób losowy trzy dowolne wierzchołki tego trójkąta i tworzymy z nich trójkąt. Obliczymy prawdopodobieństwo tego, że środek okręgu opisanego na tym wielokącie znajduje się we wnętrzu powstałego trójkąta.

Wybieramy trzy spośród $2 n + 1$ wierzchołków. Zatem:

$|Ω| = (\binom{2 n + 1}{3})$

$|Ω| = \frac{n (2 n - 1) (2 n + 1)}{3}$

Obliczymy najpierw prawdopodobieństwo zdarzenia przeciwnego $A'$ – środek okręgu opisanego na wielokącie nie należy do powstałego trójkąta.

RE9eyW785yAaf

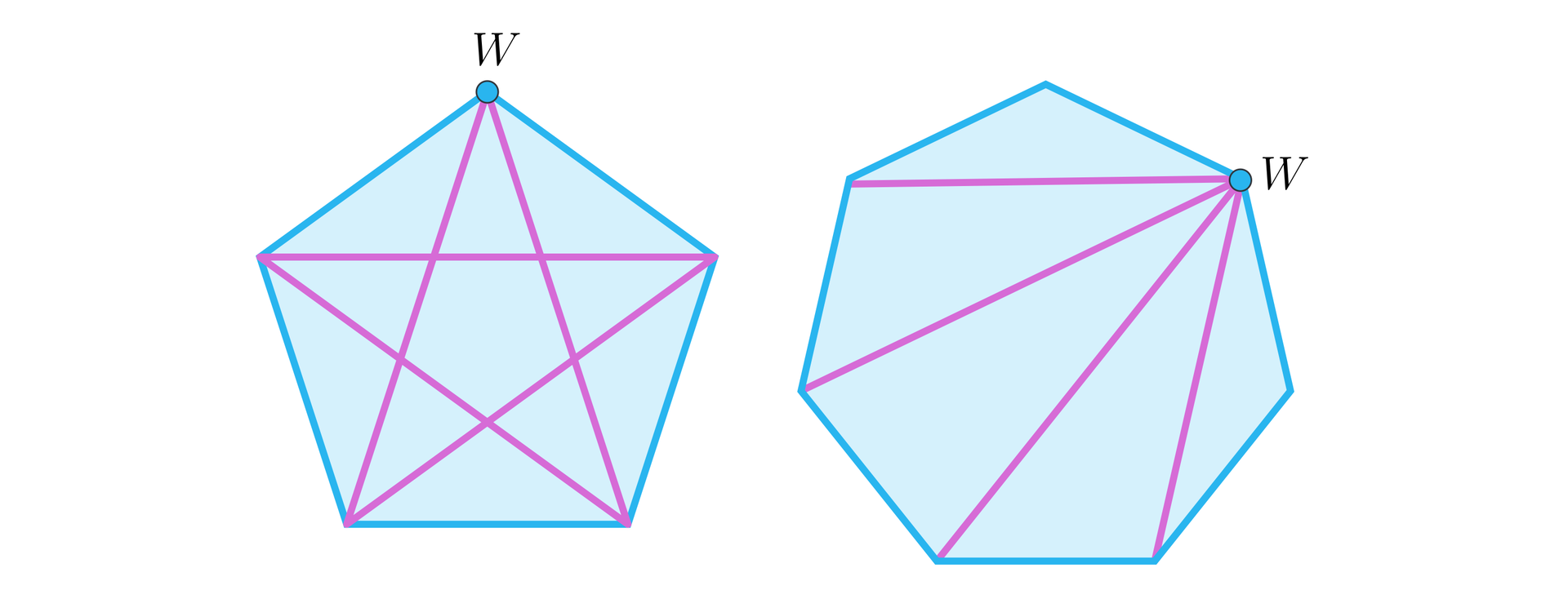
Rysunek przedstawia dwie figury, pierwszy pięciokąt w którym w środku połączono wszystkie wierzchołki ze sobą, a górny wierzchołek został oznaczony literą W. Druga figura to ośmiokąt gdzie zaznaczono jeden punkt W z którego wychodzą cztery odcinki łączące cztery wierzchołki z naprzeciwka.

Jeśli wybierzemy dowolny wierzchołek $W$ wielokąta, to istnieje dokładnie $n$ wierzchołków wielokąta o tej własności, że wybierając dowolne dwa z nich otrzymujemy trójkąt o wierzchołku kąta rozwartego w punkcie $W$ .

Zauważmy, że to właśnie te trójkąty nie zawierają środka okręgu opisanego na wielokącie. Ich liczba jest równa $(2 n + 1) \cdot (\binom{n}{2})$ . Czyli:

$|A'| = (2 n + 1) \cdot (\binom{n}{2})$

$|A'| = (2 n + 1) \cdot \frac{n (n - 1)}{2}$

Prawdopodobieństwo zajścia tego zdarzenia jest równe

$P (A') = \frac{n (2 n + 1) (n - 1)}{2} : \frac{n (2 n - 1) (2 n + 1)}{3}$

$P (A') = \frac{n (2 n + 1) (n - 1)}{2} \cdot \frac{3}{n (2 n - 1) (2 n + 1)} = \frac{3 \cdot (n - 1)}{2 \cdot (2 n - 1)}$

Oznaczmy:
$A$ – zdarzenie polegające na tym, że środek okręgu opisanego na tym wielokącie znajduje się we wnętrzu powstałego trójkąta.

$P (A) = 1 - P (A')$

$P (A) = 1 - \frac{3 \cdot (n - 1)}{2 \cdot (2 n - 1)} = \frac{4 n - 2 - 3 n + 3}{2 \cdot (2 n - 1)}$

$P (A) = \frac{n + 1}{2 \cdot (2 n - 1)}$

Odpowiedź:

Prawdopodobieństwo tego, że środek okręgu opisanego na tym wielokącie znajduje się we wnętrzu powstałego trójkąta jest równe $\frac{n + 1}{2 \cdot (2 n - 1)}$ .

Słownik

klasyczna definicja prawdopodobieństwa

niech $Ω$ będzie skończonym zbiorem wszystkich możliwych zdarzeń elementarnych jednakowo prawdopodobnych; prawdopodobieństwem zajścia zdarzenia $A \subset Ω$ nazywamy liczbę:

P (A) = \frac{|A|}{|Ω|}

Wprowadzenie

Animacja

Słownik