Przeczytaj

Różne spojrzenia na pole trójkąta

Trójkąt jest figurą, która „cieszy się szczególnymi względami” wśród autorów programów szkolnych. Pomyślcie bowiem, gdy nauczyciel w szkole poprosi o podanie wzoru na pole prostokąta jest niemal pewne, że przywołany zostanie tylko jeden – ten, w którym liczymy iloczyn długości boków: $a \cdot b$ . Raczej nikt nie powie, że pole prostokąta wyraża się np. wzorem $\frac{1}{2} \cdot d^{2} \cdot \sin φ$ , gdzie $d$ jest długością przekątnej, a $φ$ kątem między przekątnymi. Tymczasem swoistym elementarzem, w odniesieniu do trójkąta, jest nie tylko wzór, w którym liczymy połowę iloczynu długości podstawy i wysokości, ale także ten, często przywoływanym przy konstruowaniu zadań zamkniętych na maturę z matematyki, gdzie wykorzystujemy kąt między bokami, tj.: $\frac{1}{2} a b \cdot \sin ∢ (a, b)$ , czy ten najkrótszy i często nieuświadomiony: $p \cdot r$ , który łączy promień okręgu wpisanego i obwód trójkąta. Ale teraz nadszedł czas, by te wzory wykorzystać.

Przykład 1

Rozważmy trójkąt o bokach długości $5$ , $6$ , $7$ i zastanówmy się jak wiele dodatkowych informacji, związanych z tym trójkątem, da się otrzymać, przy wykorzystaniu poznanych dotychczas twierdzeń i zależności i tych, których zasoby znajdują się w dostępnym na egzaminie maturalnym zestawie wybranych wzorów matematycznych.

Zacznijmy od zastosowania wzoru Heronawzór Heronawzoru Herona. Zgodnie z przypisywaną Heronowi zależnością, pole dowolnego trójkąta opisuje wzór

$P_{△} = \sqrt{p (p - a) (p - b) (p - c)}$ , gdzie $a$ , $b$ , $c$ są długościami boków trójkąta, a $p$ jest połową jego obwodu.

W naszym przypadku mamy $p = \frac{5 + 6 + 7}{2} = 9$ oraz $P_{△} = \sqrt{9 (9 - 5) (9 - 6) (9 - 7)} = 6 \sqrt{6}$ .

Znajomość pola trójkąta i parametru $p$ – opisującego połowę jego obwodu – pozwala łatwo obliczyć promień $r$ okręgu wpisanego w ten trójkąt. Skorzystamy ze wzoru

$P_{△} = p \cdot r$ ,

który także cytowany jest w przywołanym zestawie wzorów. Mamy zatem:

$6 \sqrt{6} = 9 \cdot r$ , stąd $r = \frac{6 \sqrt{6}}{9} = \frac{2 \sqrt{6}}{3}$ .

Ponieważ pole trójkąta o bokach długości $a$ , $b$ , $c$ i promieniu $R$ okręgu opisanego na trójkącie opisuje wzór

$P_{△} = \frac{a b c}{4 R}$ ,

więc $R = \frac{a b c}{4 P_{△}}$ .
W naszym przypadku otrzymujemy: $R = \frac{5 \cdot 6 \cdot 7}{4 \cdot 6 \sqrt{6}} = \frac{35}{4 \sqrt{6}}$ .

Przed nami jest wyznaczenie miar kątów naszego trójkąta. Ponieważ

$\frac{a}{\sin α} = 2 R$ ,

więc w szczególności: $\frac{5}{\sin α} = 2 \cdot \frac{35}{4 \sqrt{6}}$ .

Stąd $\sin α = \frac{10 \sqrt{6}}{35} = \frac{2 \sqrt{6}}{7} \approx 0, 6999$ , zatem $α \approx 44 °$ .
Podobnie $\frac{6}{\sin β} = 2 \cdot \frac{35}{4 \sqrt{6}}$ , zatem $\sin β = \frac{12 \sqrt{6}}{35} \approx 0, 8398$ oraz $β \approx 57 °$ . Z bilansu kątów w trójkącie wynika, że trzeci z kątów ma przybliżona miarę równą: $180 ° - 44 ° - 57 ° = 79 °$ .

Uwaga

Niebawem wyznaczenie miar kątów trójkąta o danych bokach będzie możliwe bez wyznaczania jego pola – przydatne będzie twierdzenie cosinusówtwierdzenie Carnotatwierdzenie cosinusów – tymczasem jednak to właśnie pole stanowi punkt wyjścia do dalszych obliczeń. Warto jednak nadmienić, że aby wyznaczyć miary kątów nie ma potrzeby wyznaczać promienia okręgu opisanego – wystarczy zastosować inny wzór na pole trójkąta: $P_{△} = \frac{1}{2} a b \sin γ$ , gdzie oczywiście $a$ , $b$ są długościami boków, a $γ$ jest miarą kąta leżącego między tymi bokami.
Rozwiążemy teraz zadanie, w którym wyznaczeniu polu czworokąta będzie towarzyszyło zastosowanie twierdzenia sinusówtwierdzenie Snelliusatwierdzenia sinusów, a sam czworokąt potraktujemy jako „sumę” dwóch trójkątów (użycie cudzysłowu w słowie suma nie jest konieczne, bowiem czworokąt jest w istocie sumą mnogościową dwóch trójkątów).

Przykład 2

Rozważmy analogiczny problem jak w przykładzie $1$ , ale przygotowaniem do zastosowania twierdzenia sinusów będą jedynie definicje funkcji trygonometrycznych w trójkącie prostokątnym i twierdzenie Pitagorasa (unikniemy tym samym sięgania do wzoru Herona).

Rozważmy trójkąt o bokach długości $16$ , $20$ , $24$ . Wyznaczymy jego pole, promień okręgu opisanego i wartości sinusów kątów tego trójkąta.

Przyjmijmy oznaczenia jak na rysunku, gdzie $h$ jest wysokością poprowadzoną na bok $b$ , a $x$ i $y$ są długościami odcinków, na jakie spodek tej wysokości podzielił podstawę. Mamy wówczas, że $x + y = 24$ .

R1TF5wVKS4a3Q

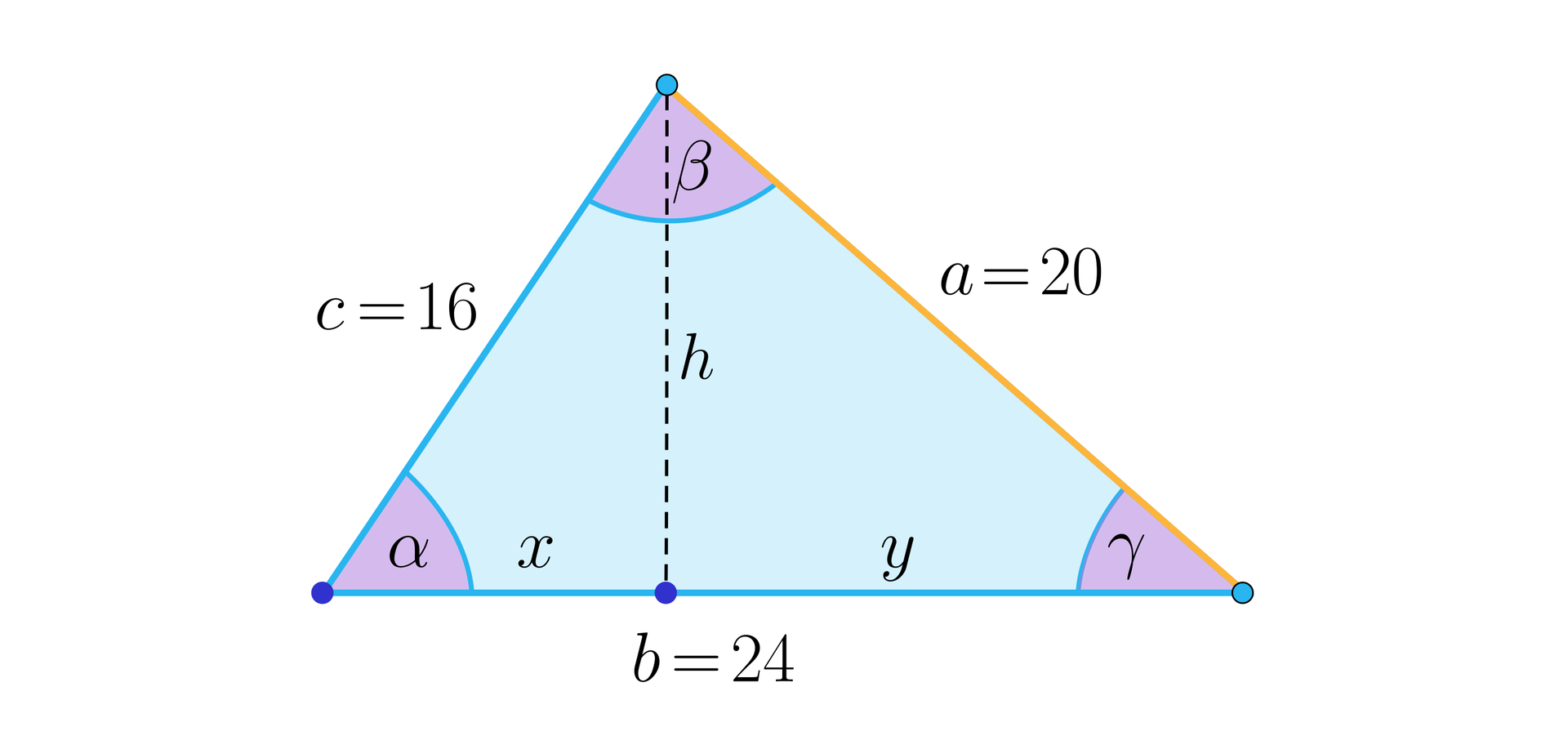
Ilustracja przedstawia trójkąt o podstawie b, która ma długość 24, prawym boku a o długości 20 i lewym c o długości 16. Kąty wewnętrzne w trójkącie to: między bokami c i b kąt alfa, między bokami b i a kąt gama, między bokami a i c kąt beta. Z górnego wierzchołka upuszczona jest wysokość h dzieląca podstawę b na dwa odcinki: x oraz y.

Trójkąty o bokach $x$ , $h$ , $c$ oraz $y$ , $h$ , $a$ są oczywiście prostokątne, dlatego możemy zapisać równości

$h^{2} = c^{2} - x^{2}$ oraz $h^{2} = a^{2} - y^{2}$ .

Stąd mamy $c^{2} - x^{2} = a^{2} - y^{2}$ , czyli $16^{2} - x^{2} = 20^{2} - y^{2}$ .

Pozwala to zbudować układ równań $\{\begin{cases} x + y = 24 \\ 256 - x^{2} = 400 - y^{2} \end{cases}$ .

Ponieważ $y = 24 - x$ , więc możemy drugą równość zapisać w postaci $256 - x^{2} = 400 - {(24 - x)}^{2}$ .

Po uproszczenie przyjmuje ona postać $256 - 400 + 576 = 48 x$ .

Stąd $x = 9$ oraz $h^{2} = 256 - 81 = 175$ . Zatem $h = 5 \sqrt{7}$ oraz $\sin α = \frac{5 \sqrt{7}}{16}$ .

Pole trójkąta jest więc równe: $P_{△} = \frac{1}{2} \cdot 24 \cdot 5 \sqrt{7} = 60 \sqrt{7}$ .

Promień okręgu opisanego na tym trójkącie jest równy: $R = \frac{20}{2 \cdot \frac{5 \sqrt{7}}{16}} = \frac{32}{\sqrt{7}}$ .

Korzystając ponownie z twierdzenia sinusów możemy wyznaczyć sinusy pozostałych kątów tego trójkąta:

$\sin β = \frac{\frac{5 \sqrt{7}}{16} \cdot 24}{20} = \frac{3 \sqrt{7}}{8}$ , $\sin γ = \frac{\frac{5 \sqrt{7}}{16} \cdot 16}{20} = \frac{\sqrt{7}}{4}$ .

Przykład 3

Rozważmy trapez wpisany w okrąg o promieniu $R = 12$ , którego kąt ma miarę $75 °$ , a jego przekątna tworzy z podstawą kąt o mierze $30 °$ . Naszym zadaniem jest obliczenie pola tego trapezu. Przyjmijmy oznaczenia jak na rysunku.

R1UJZHV0dh6B5

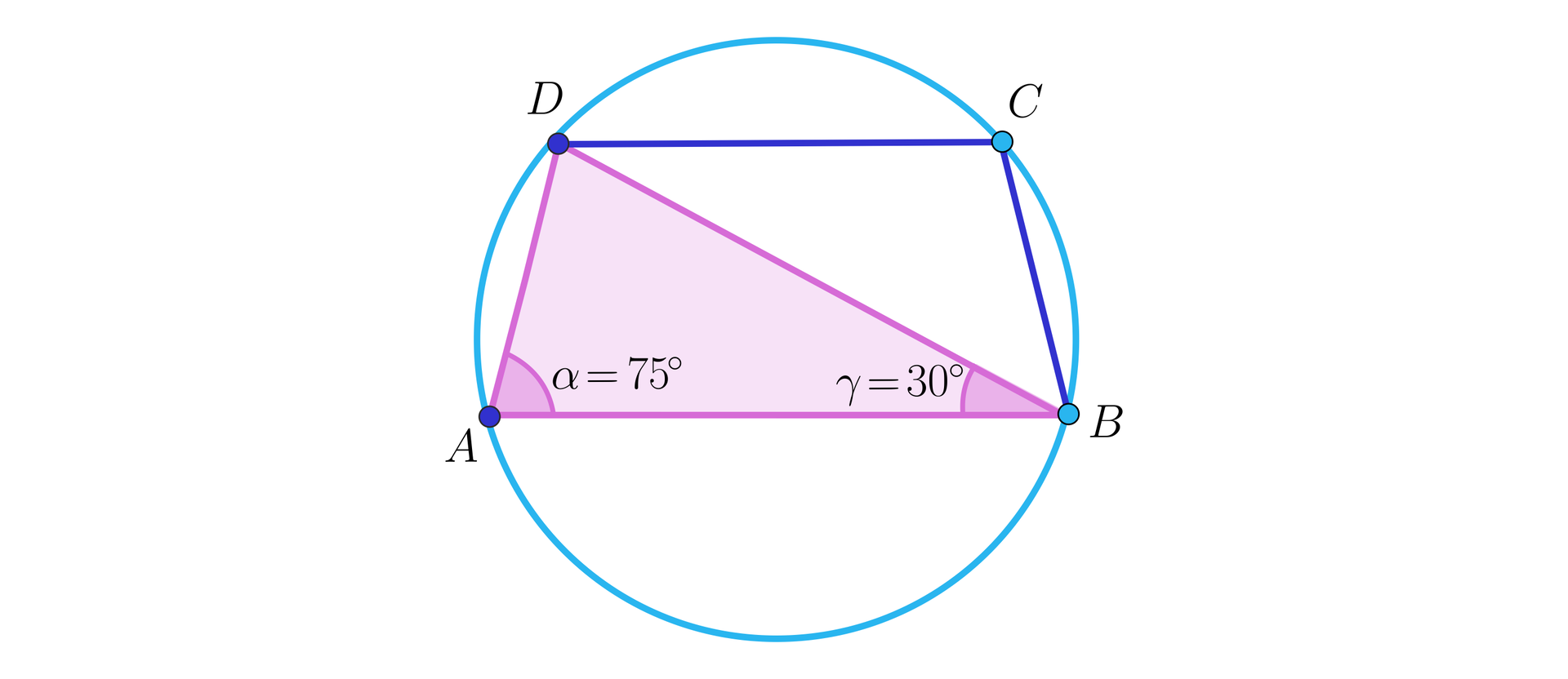
Ilustracja przedstawia okrąg, na którym zaznaczone są punkty: A, B, C i D. Punkty te połączone są odcinkami, które tworzą trapez równoramienny o dolnej podstawie A B i górnej podstawie DC. Trapez podzielony jest na dwa trójkąty przekątną D B. Trójkąt A B D jest zaznaczony kolorem fioletowym. Przy wierzchołku A zaznaczony jest kąt alfa o mierze 75 stopni. Przy wierzchołku B zaznaczony jest kąt gama o mierze 30 stopni.

Na początku musimy przypomnieć, że każdy trapez wpisany w okrąg jest równoramienny, zatem możemy rozważać dowolną z jego dwóch przekątnych, np. $B D$ . Należy także zauważyć, że trójkąt $A B D$ jest wpisany w ten sam okrąg, co dany trapez, zatem

$\frac{|A D|}{\sin 30 °} = 2 R = 24$ ,

a ramię trapezu ma długość $|A D| = 24 \cdot \frac{1}{2} = 12$ .

Ponieważ $|∢ A D B| = 180 ° - 75 ° - 30 ° = 75 °$ , więc $\frac{|A B|}{\sin 75 °} = 24$ .

Stąd $|A B| = |B D| = 24 \cdot \sin 75 °$ .

Oczywiście moglibyśmy wyznaczać długość wysokości trapezu i jego krótszej podstawy, ale dla ułatwienia skorzystamy z faktu, że pole trapezu jest równe sumie pól trójkątów $A B D$ i $B C D$ .

Zatem $P_{A B C D} = P_{A B D} + P_{B C D} = \frac{1}{2} \cdot |A B| \cdot |B D| \cdot \sin 30 ° + \frac{1}{2} \cdot |B C| \cdot |B D| \cdot \sin 45 °$ .

Stąd $P_{A B C D} = \frac{1}{2} \cdot 24 \cdot \sin 75 ° \cdot (24 \cdot \sin 75 ° \cdot \frac{1}{2} + 12 \cdot \frac{\sqrt{2}}{2}) =$
$= 12 \cdot \sin 75 ° \cdot (12 \cdot \sin 75 ° + 6 \sqrt{2})$ .

Jeśli „przeszkadza” nam zapis $\sin 75 °$ , jako oznaczenie pewnej liczby, to możemy podstawić przybliżoną wartość z tablic $(0, 9659)$ lub uwierzyć (przy zagadnieniach z trygonometrii będzie to wyjaśnione), że $\sin 75 ° = \frac{\sqrt{6} + \sqrt{2}}{4}$ .

Słownik

wzór Herona

wzór pozwalający obliczyć pole trójkąta, jeśli znane są długości $a$ , $b$ , $c$ jego boków; niech $p = \frac{a + b + c}{2}$ oznacza połowę obwodu trójkąta – wtedy pole $S$ wynosi: $S = \sqrt{p (p - a) (p - b) (p - c)}$

twierdzenie Snelliusa

w matematyce zamienna nazwa twierdzenia sinusów, określającego związek między bokami i kątami w trójkącie.

twierdzenie Carnota

w matematyce zamienna nazwa twierdzenia cosinusów, określającego związek między kątem i bokami w trójkącie

Wprowadzenie

Prezentacja multimedialna

Różne spojrzenia na pole trójkąta

Słownik