Wyznaczymy wymiary prostokąta o obwodzie $60 \mathrm{cm}$ i największym polu.

Rozwiązanie

W pierwszym etapie dążymy do opisania pola za pomocą funkcji jednej zmiennej. Oznaczmy $a$ i $b$ jako boki prostokąta. Zatem $a$ i $b$ muszą być liczbami dodatnimi, ponieważ długości boków figury nie mogą być ujemne. Zapiszmy obwód w postaci równania $2a+2b=60$. Wyznaczmy jedną zmienną np. $b$, otrzymujemy $b=30-a$. Skoro $b>0$, to $a\in \left(0,30\right)$.

Pole prostokąta wynosi $a·b$. Podstawiając otrzymujemy funkcję zależną od $a$:

$P\left(a\right)=a\left(30-a\right)$.

$D=\left(0, 30\right)$.

Naszkicujemy wykres funkcji, współczynnik przy najwyższej potędze jest ujemny, więc ramiona paraboli skierowane są w dół.

RsntKYnThleZP

Ilustracja przedstawia układ współrzędnych z poziomą osią X oraz z pionową osią Y, głównie pierwszą ćwiartkę. Na płaszczyźnie przedstawiono parabolę o wierzchołku w pierwszej ćwiartce i o ramionach skierowanych w dół. Miejsca zerowe 0 oraz 30 zaznaczono niezamalowanymi kółkami, a część wykresu znajdującą się w pierwszej ćwiartce wyróżniono kolorem.

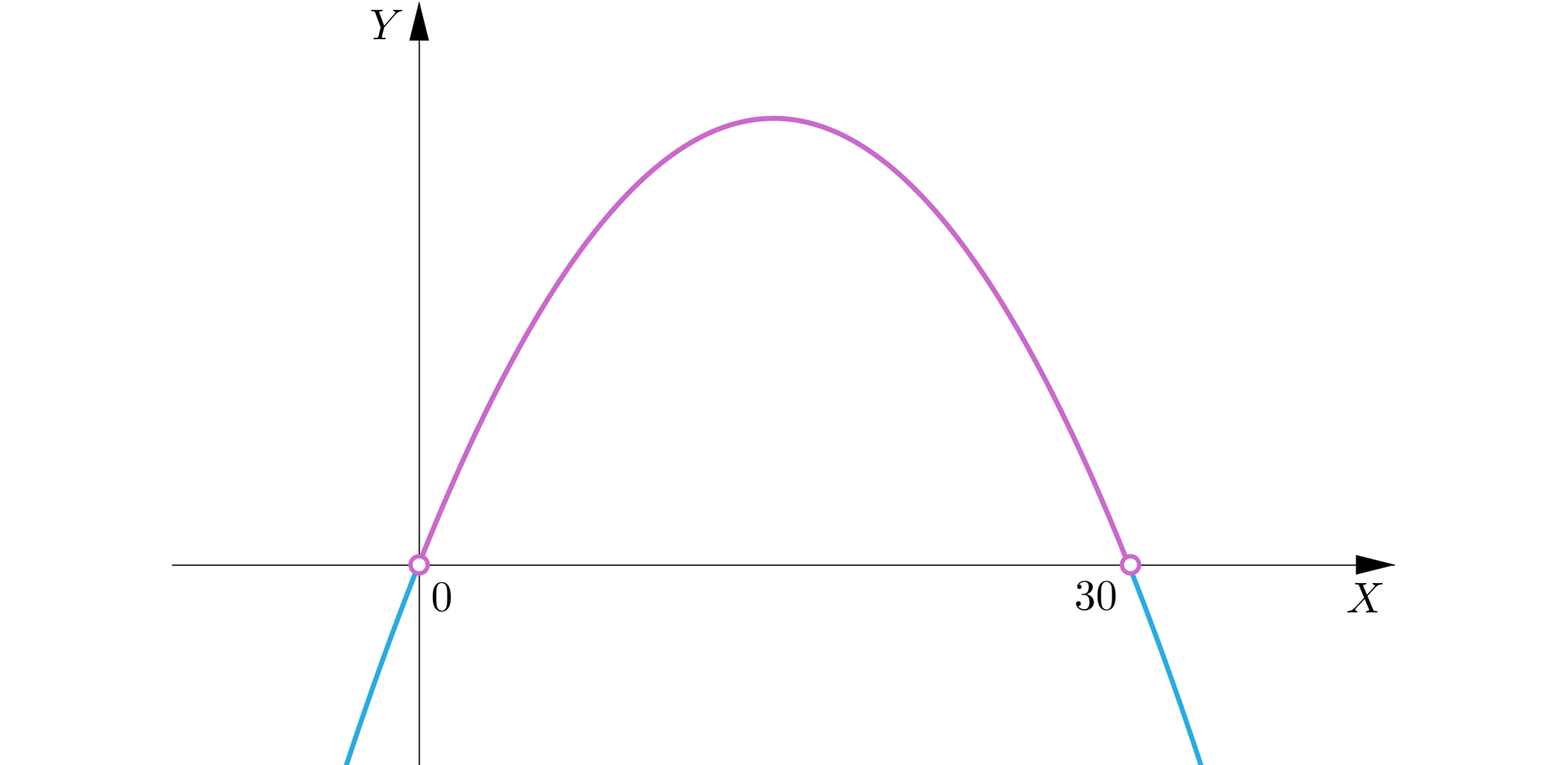
Pierwsza współrzędna wierzchołka paraboli $a_w$, jest średnią miejsc zerowych funkcji $y=a\left(30-a\right)$, zatem $a_w=\frac{0+30}{2}=15$. Zauważmy, że $a_w$ należy do dziedziny, zatem największa wartość funkcji jest przyjmowana w wierzchołku paraboli. Wyznaczymy $b=30-15=15$.

Odpowiedź

Wymiary prostokąta to $15 \mathrm{cm}\times 15 \mathrm{cm}$.

Wyznaczymy liczby, których różnica jest równa $8$ tak, by suma ich kwadratów była najmniejsza.

Rozwiązanie

Oznaczmy:
$x$, $y$ – szukane liczby.

Z treści zadania wiemy, że $x-y=8$. Szukamy najmniejszej wartości wyrażenia $x^2+y^2$. W tym celu wyznaczmy jedną ze zmiennych np. $y=x-8$ i rozważmy funkcję jednej zmiennej

$f\left(x\right)=x^2+{\left(x-8\right)}^2$.

Sprowadzając funkcję $f\left(x\right)$ do postaci ogólnej mamy:

$f\left(x\right)=2x^2-16x+64$.

W tym przykładzie nie mamy żadnych warunków nałożonych na zmienne $x$ i $y$, więc dziedziną jest zbiór liczb rzeczywistych.

Wykresem funkcji $f$ jest parabla, której ramiona skierowane są w górę. Wartość najmniejsza jest więc przyjmowana w wierzchołku. Obliczając pierwszą współrzędną wierzchołka paraboli ze wzoru:

$x_w=-\frac{b}{2a}$,

otrzymamy $x_w=-\frac{-16}{2·2}=4$. Zatem jedna z liczb jest równa $4$.

Obliczamy drugą liczbę $y=4-8=-4$.

Odpowiedź

Szukane liczby to $\left(-4\right)$ i $4$.

Przekrój osiowy walca jest prostokątem o obwodzie $14$. Obliczymy największe możliwe pole powierzchni bocznej tego walca.

Rozwiązanie

Oznaczmy:
$H$ – wysokość walca,
$r$ – promień podstawy walca.

RXNpzcCmrLRVU

Ilustracja przedstawia walec o wysokości H i o średnicy podstawy równej 2 r.

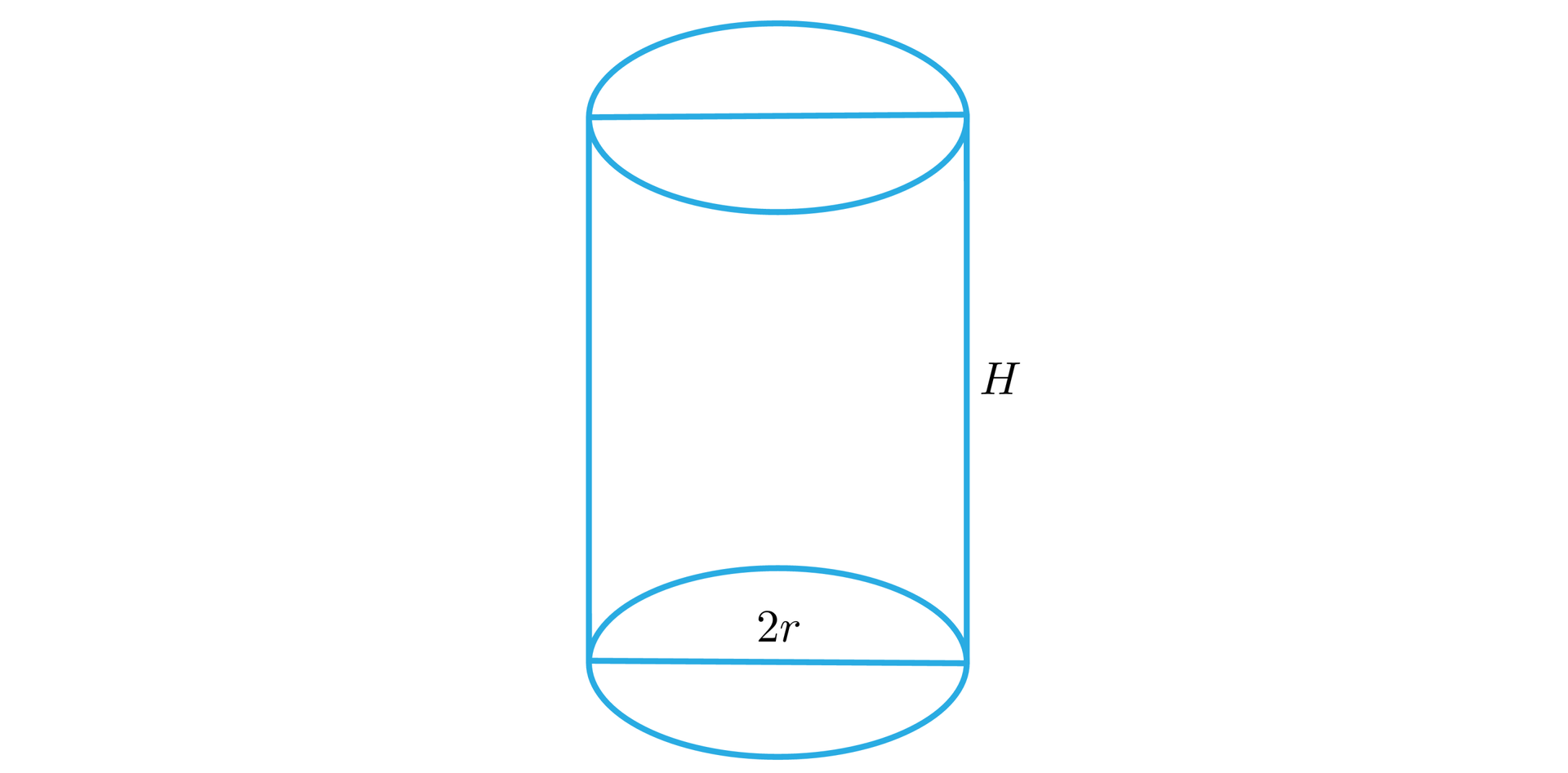
Obwód prostokąta możemy zapisać $2H+4r=14$. Pole powierzchni bocznej walca możemy wyliczyć ze wzoru:

$P_b=2\pi rH$.

Ze wzoru na obwód prostokąta wyliczamy, że $2r=7-H$. Podstawiając $7-H$ w miejsce $2r$ otrzymujemy pole powierzchni bocznej jako funkcję zmiennej $H$.

$P_b\left(H\right)=\pi \left(7-H\right)H$.

Ponieważ wysokość walca i promień jego podstawy są liczbami dodatnimi, więc dziedziną funkcji jest zbiór $D: H\in \left(0, 7\right)$.

Naszkicujemy wykres funkcji kwadratowej, której wykres pokrywa się z funkcją $H$ w jej dziedzinie.

R16Id2sANrfGx

Ilustracja przedstawia układ współrzędnych z poziomą osią X oraz z pionową osią Y, głównie pierwszą ćwiartkę. Na płaszczyźnie przedstawiono parabolę o wierzchołku w pierwszej ćwiartce i o ramionach skierowanych w dół. Miejsca zerowe 0 oraz 7 zaznaczono niezamalowanymi kółkami, a część wykresu znajdującą się w pierwszej ćwiartce wyróżniono kolorem.

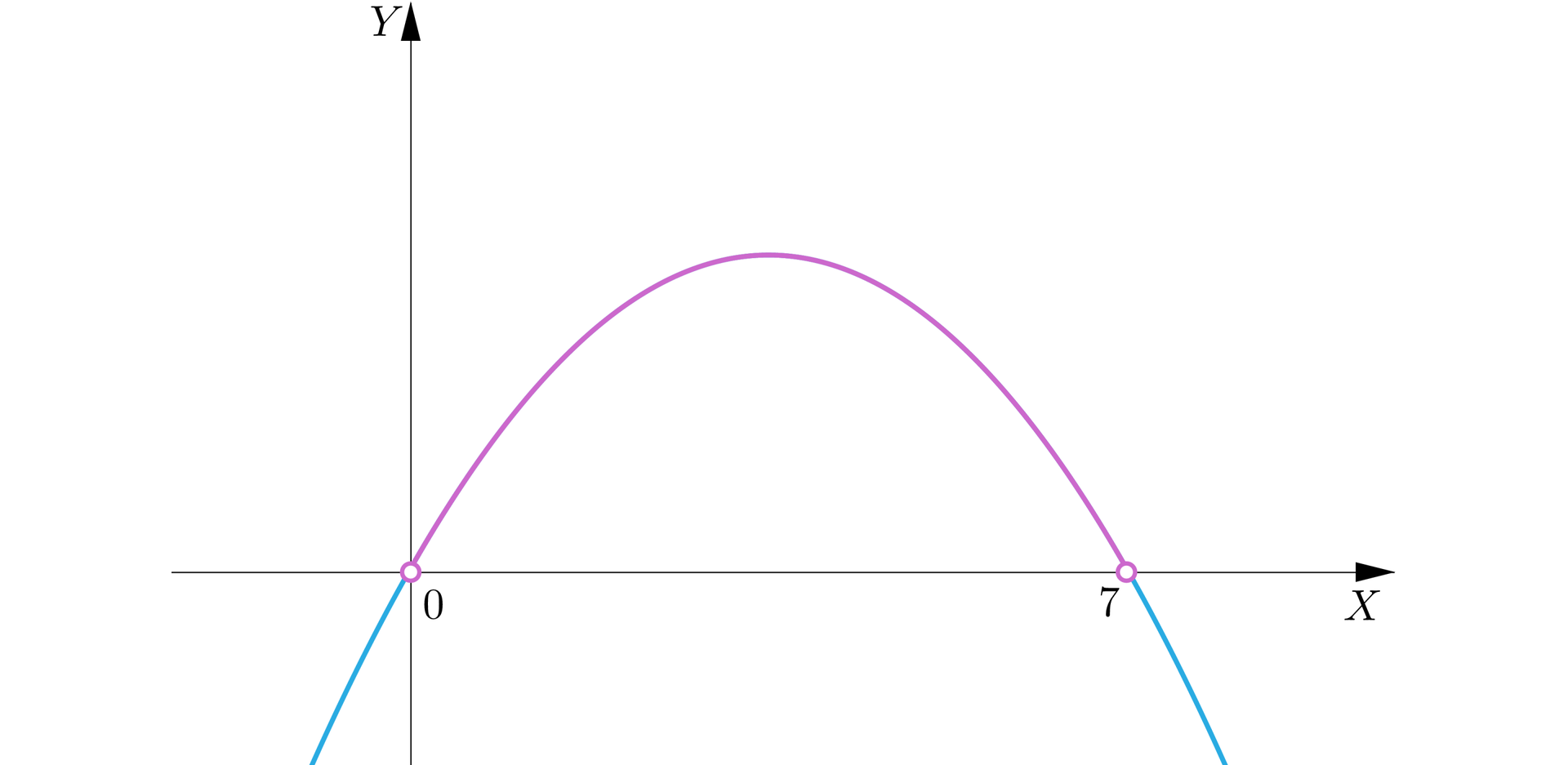
Pierwsza współrzędna wierzchołka paraboli $H_w$ , jest średnią arytmetyczną miejsc zerowych, zatem $H_w=\frac{0+7}{2}=3,5 \mathrm{cm}$. Możemy zauważyć, że należy do dziedziny funkcji, zatem funkcja przyjmuje największą wartość w wierzchołku paraboli. Następnie wyznaczymy największe możliwe pole. Podstawmy wyliczoną wysokość do wzoru na pole powierzchni bocznej walca:

$P_b\left(H\right)=\pi \left(7-3,5\right)·3,5=12,25\pi$.

Odpowiedź

Największe możliwe pole wynosi $12,25\pi$.

Wysokość prostopadłościanu jest równa $3 \mathrm{cm}$, a jego podstawą jest prostokąt o obwodzie $18 \mathrm{cm}$. Obliczymy wymiary podstawy oraz objętość prostopadłościanu, którego pole powierzchni całkowitej jest największe.

Rozwiązanie

Oznaczmy przez $x$ i $y$ długości krawędzi podstawy.

R1MzMRrH4s4AF

Ilustracja przedstawia prostopadłościan o prostokątnej podstawie o wymiarach y na x oraz o wysokości równej 3 centymetry.

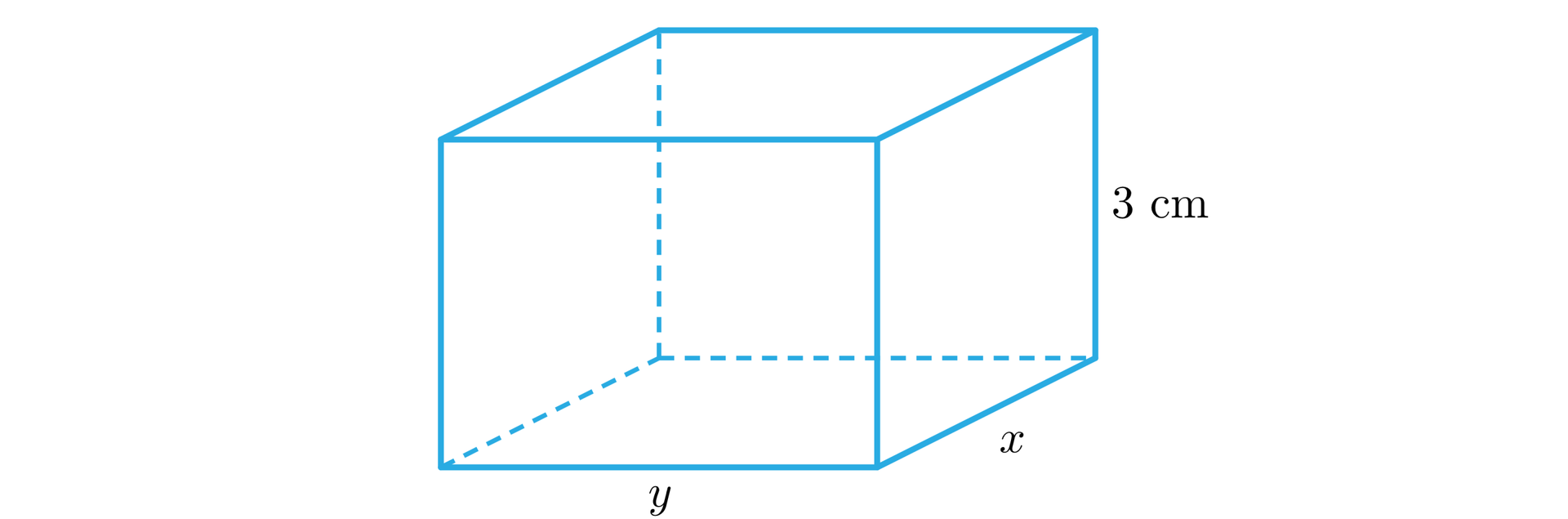
Zapisując obwód w postaci równania otrzymujemy $2x+2y=18$. Pole powierzchni prostopadłościanu wynosi:

$P_c=2xy+6x+6y$.

Wyznaczamy jedną zmienną z równania obwodu np. $y=9-x$ i podstawiamy do wzoru na pole powierzchni całkowitej:

$P_c\left(x\right)=2x\left(9-x\right)+6x+6\left(9-x\right)=-2x^2+18x+54$.

Długości krawędzi muszą być dodatnie, więc $y=9-x>0$, więc dziedziną funkcji jest:

$D: x\in \left(0, 9\right)$.

Powstała funkcja kwadratowa ma ramiona skierowane w dół, więc wartość największą przyjmuje w wierzchiłku. Dlatego obliczymy pierwszą współrzędną wierzchołka paraboli ze wzoru:

$x_w=-\frac{b}{2a}$,

otrzymamy $x_w=-\frac{18}{-4}=4,5$, czyli należy do dziedziny funkcji. Prostokąt w  podstawie ma więc wymiary $4,5 \mathrm{cm}\times 4,5 \mathrm{cm}$.

Policzymy objętość prostopadłościanu ze wzoru:

$V=xyH$.

Podstawiając otrzymujemy $V=4,5\cdot 4,5\cdot 3=60,75{\mathrm{c}\mathrm{m}}^3$.

to funkcja określona wzorem:

gdzie współczynniki $a$, $b$, $c$ są ustalonymi liczbami przy czym $a\ne 0$

to maksymalna lub minimalna wartość funkcji