Przeczytaj
Wielościanem nazywamy bryłę przestrzenną, której wszystkie ściany są wielokątami.
Poniżej przedstawiono bryły, które są wielościanamiwielościanami. Przyjrzyj im się uważnie. Wszystkie ściany są wielokątami – niekoniecznie takimi samymi.
-

ściany są trójkątami i pięciokątami
-

ściany są trójkątami
-

ściany są trójkątami
-

sześć ścian to trójkąty, jedna ściana to sześciokąt
-
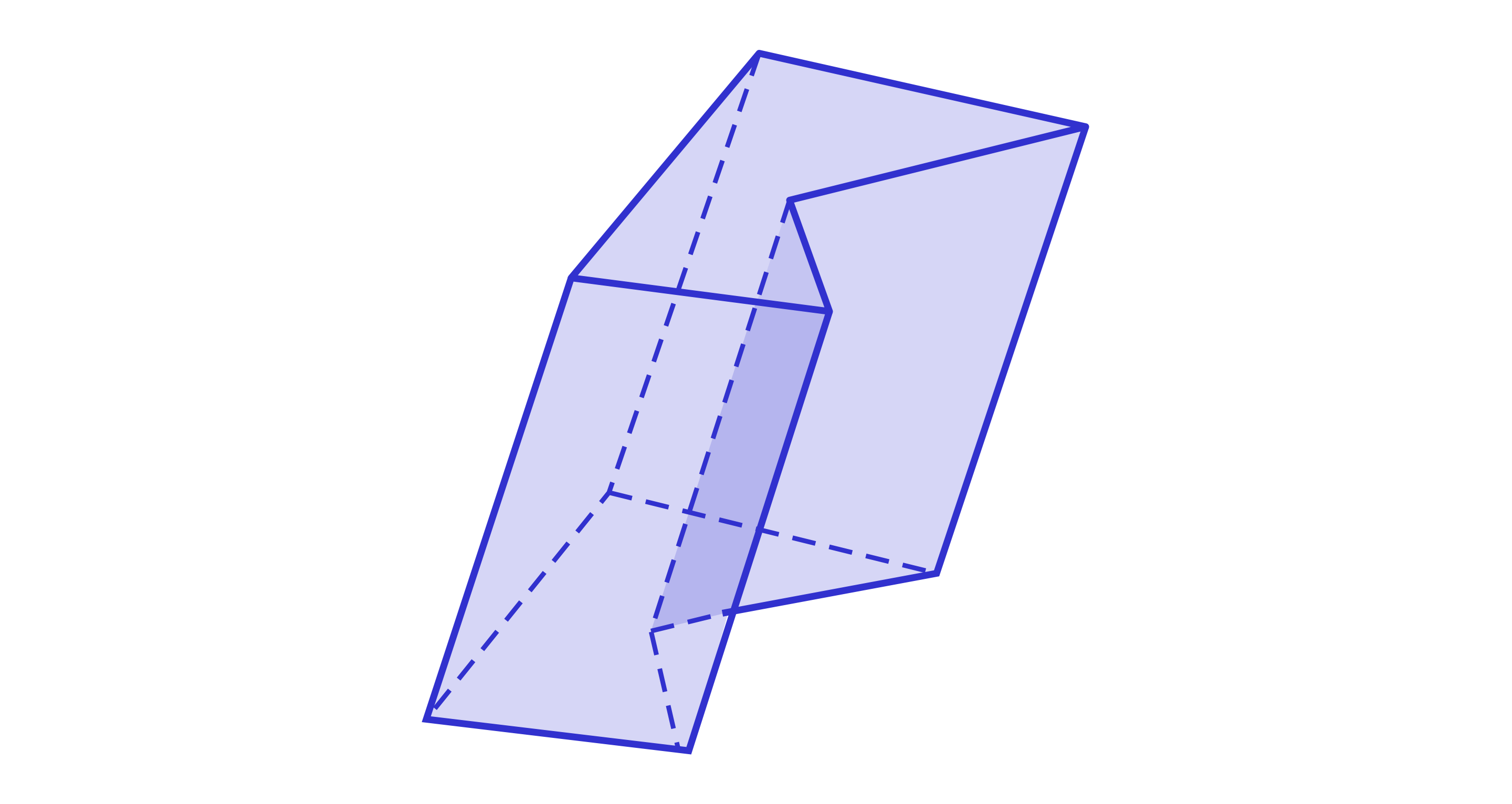
dwie ściany są pięciokątami, pozostałe – równoległobokami
-
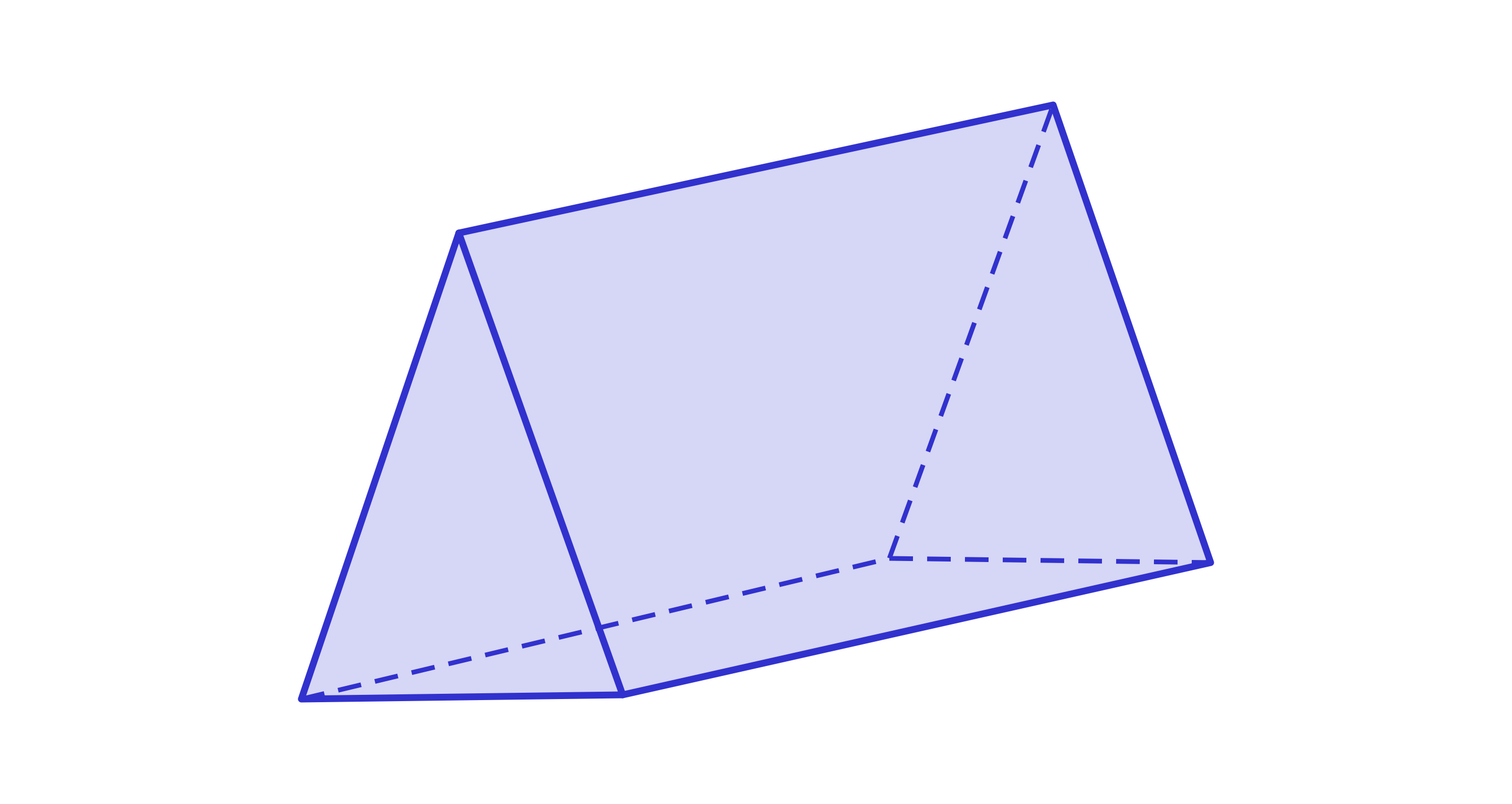
dwie ściany są trójkątami, a trzy – prostokątami
-
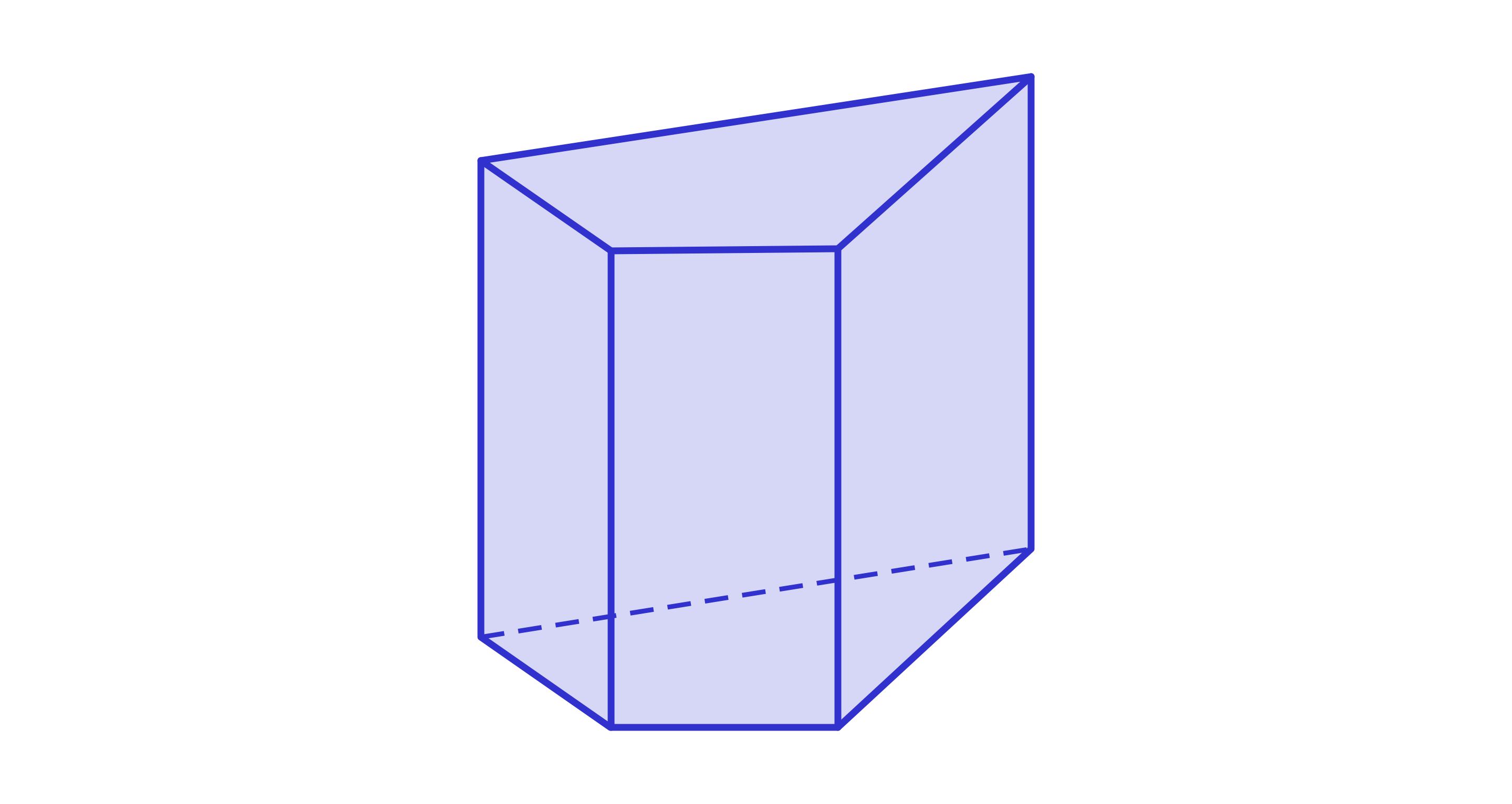
ściany są czworokątami
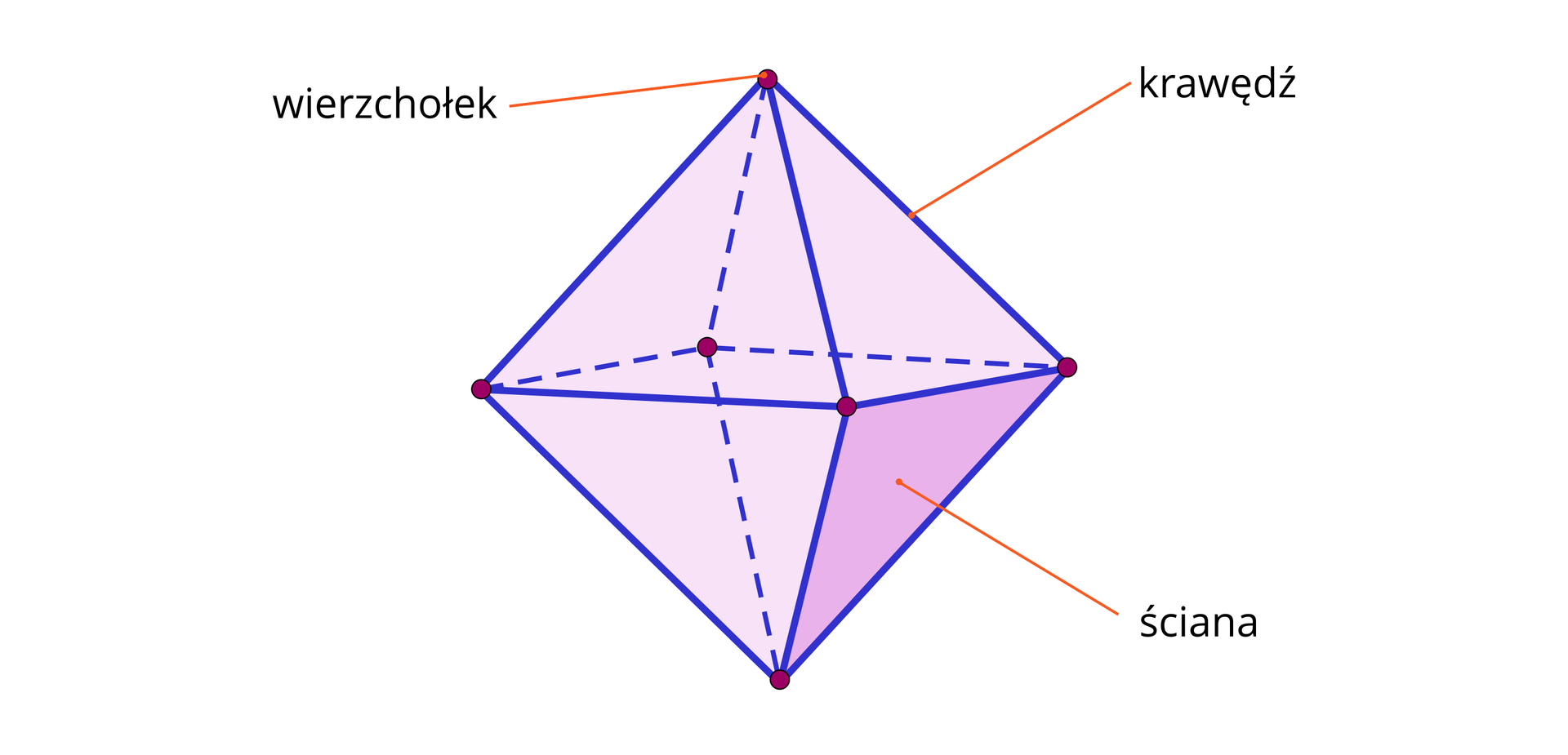
Obserwując wielościan, możemy zauważyć następujące elementy:
wierzchołki
krawędzie
ściany
Dla bryły przedstawionej na rysunku ustalimy liczbę wierzchołków, krawędzikrawędzi i ścian.
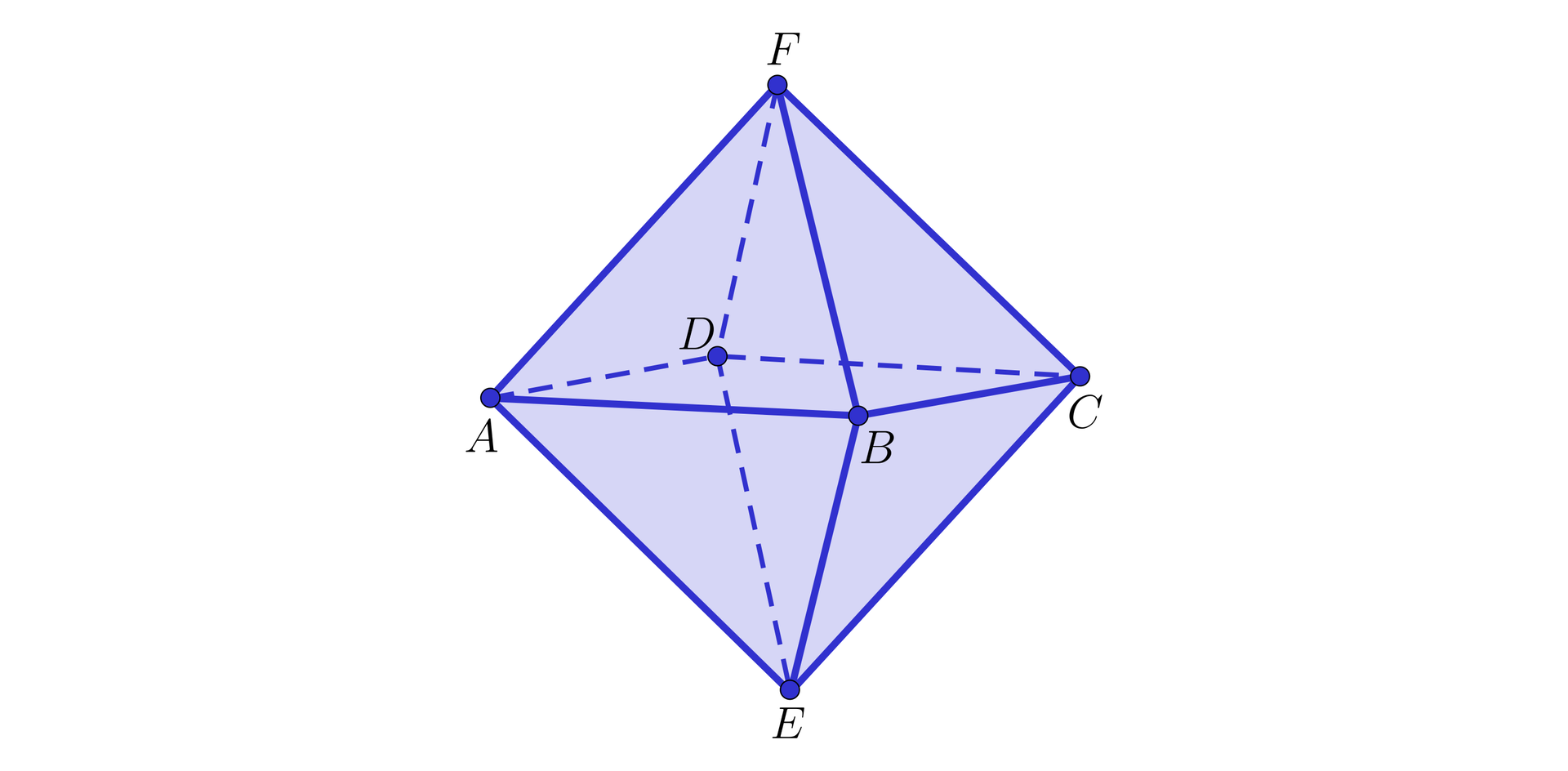
Gdy przyjrzymy się bryle na rysunku, możemy zauważyć następujące elementy:
wierzchołki, czyli punkty: , , , , ,
krawędzie, czyli odcinki: , , , , , , , , , , ,
ściany, czyli wielokąty: , , , , , , ,
Bryła przedstawiona na rysunku ma zatem wierzchołków, krawędzi i ścian, które są trójkątami.
Dla bryły przedstawionej na rysunku ustalimy liczbę wierzchołków, krawędzi i ścian.
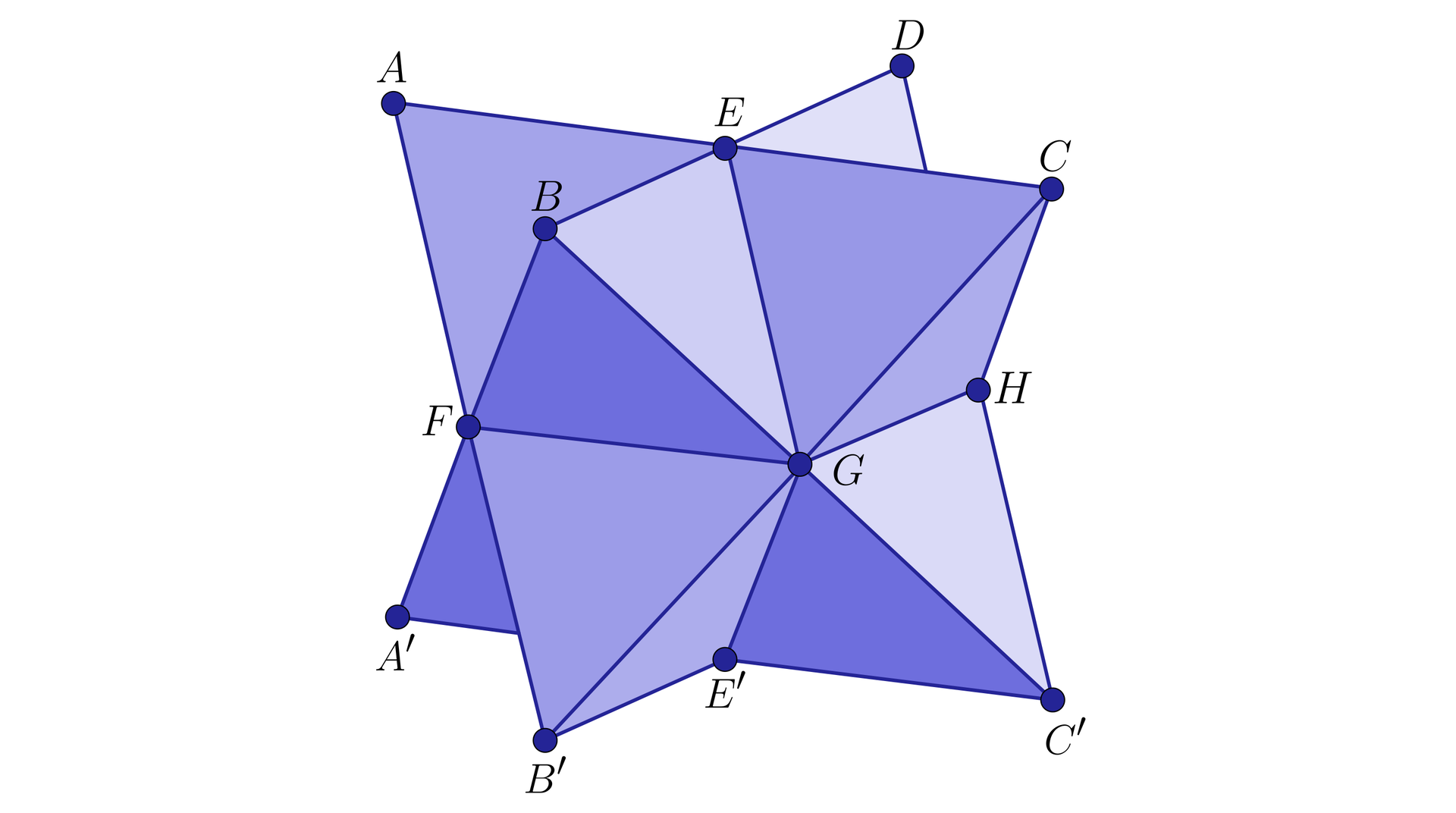
Zaczniemy od wyznaczenia liczby wierzchołków. W górnej części bryły w jednej płaszczyźnie leży wierzchołków – są to: , , , oraz . Dla uproszczenia wierzchołki, które leżą w jednej płaszczyźnie w dolnej części bryły zostały zaznaczone „primami” – są to: , , , oraz (wierzchołek nie jest widoczny). Przez środek bryły można poprowadzić kolejną płaszczyznę, w której leżą wierzchołki: , , oraz (niewidoczny).
Gdy znamy już liczbę wierzchołków, możemy stwierdzić, że wielościan ma krawędzi ( widoczne na rysunku, pozostałe są niewidoczne) i ściany, które są trójkątami równobocznymi.
Nazwa tej bryły to stella octangula (ośmiościan gwiaździsty).
Poniższe bryły mają taką samą liczbę wierzchołków, krawędzi oraz ścian, które są prostokątami.
W przypadku bryły : jeżeli wybierzemy dowolne dwa punkty bryły i połączymy je odcinkiem, to cały ten odcinek zawiera się w tej bryle. Inaczej to wygląda w przypadku wielościanu . Bez problemu możemy znaleźć takie dwa punkty bryły, że odcinek, który je łączy, nie zawiera się całkowicie w bryle (na przykład odcinek ).
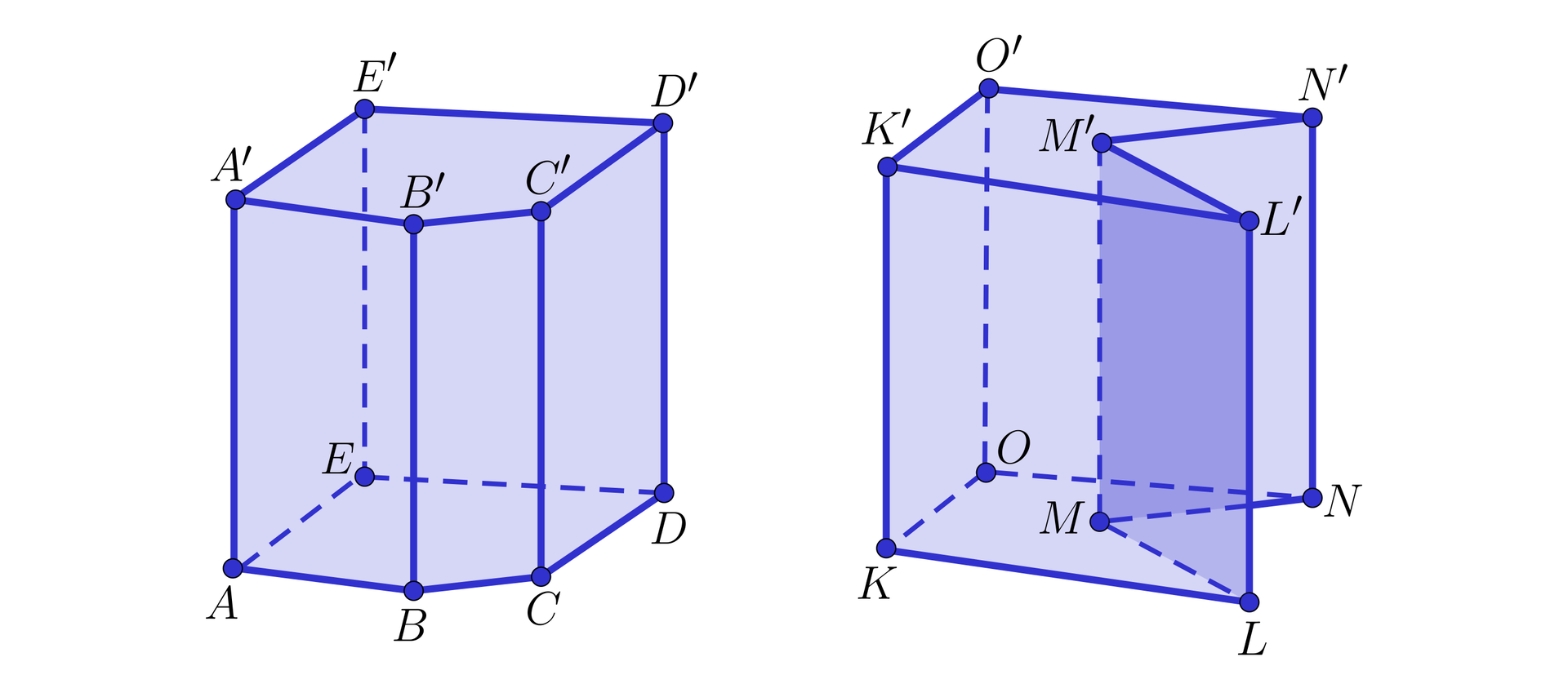
Wielościany możemy więc podzielić na dwie grupy: wypukłewypukłe i wklęsłewklęsłe.
Wielościan
wypukły - dowolne dwa punkty wielościanu tworzą odcinek, który w całości zawiera się w bryle

wklęsły - istnieje przynajmniej jeden odcinek utworzony przez punkty wielościanu, który nie zawiera się w całości w bryle

Gdy połączymy wierzchołki wielościanu, otrzymamy jeden z odcinków:
krawędź
przekątną ścianyprzekątną ściany
przekątną wielościanuprzekątną wielościanu
Jak sama nazwa wskazuje, przekątna ściany to odcinek łączący dwa wierzchołki bryły, które nie sąsiadują ze sobą, zawierający się w ścianie (wieloboku). Z kolei przekątna wielościanu to odcinek, który łączy wierzchołki bryły i nie należy do jej ściany.

Z określenia wielościanu wypukłego oraz przekątnej wielościanu wynika następująca własność.
Wielościan jest wypukły, gdy zawiera każdą swoją przekątną.
Zastanów się, czy każdy wielościan ma przekątne? Czy w każdym wielościanie występują przekątne ścian?
Wielościan przedstawiony na poniższym rysunku posiada zarówno przekątne wielościanu, jak i przekątne ścian.
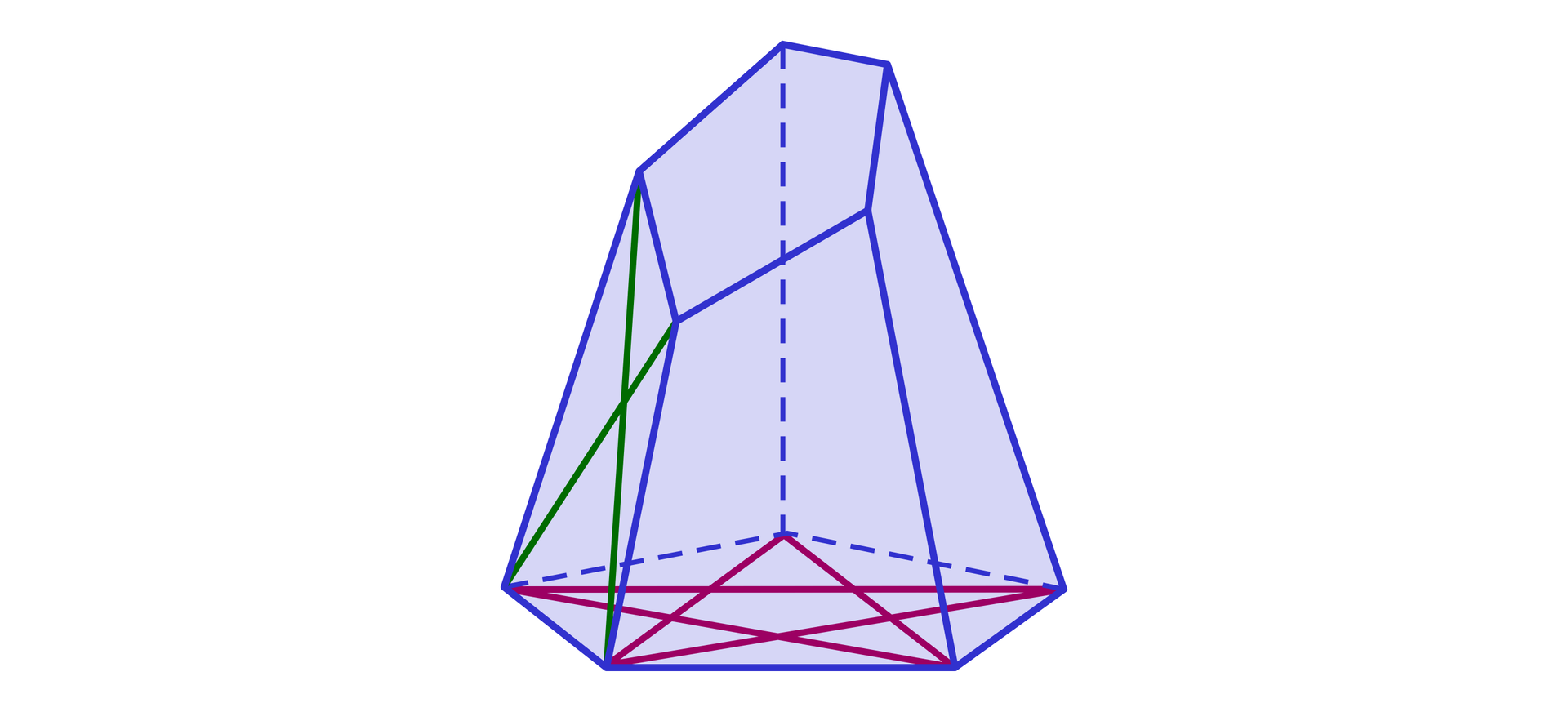
Każda z pięciu ścian, która jest czworokątem, ma dwie przekątne.
Pozostałe dwie ściany są pięciokątami, więc każda z nich ma pięć przekątnych.
W sumie wielościan przedstawiony na rysunku ma 20 przekątnych ścian.
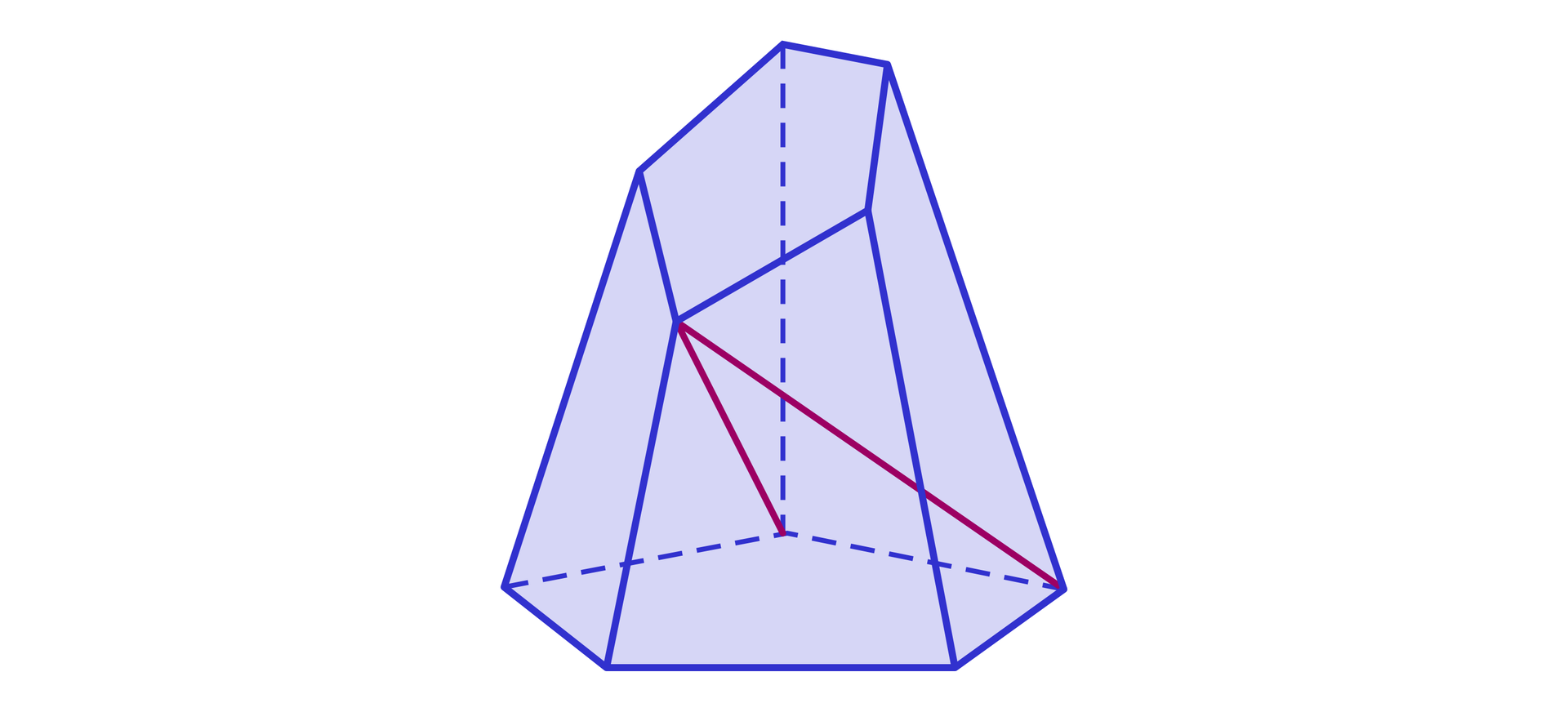
Zauważmy, że z każdego wierzchołka górnego pięciokąta można poprowadzić dwa odcinki do wierzchołków dolnego pięciokąta, tak aby odcinki te nie zawierały się w ścianie bryły. W ten sposób można utworzyć przekątnych bryły.
Zastanów się, dlaczego w tym przypadku nie musimy tego rozumowania powtarzać dla wierzchołków z dolnego pięciokąta.
Czworościan jest przykładem wielościanu, który nie ma ani jednej przekątnej zarówno ściany, jak i bryły.

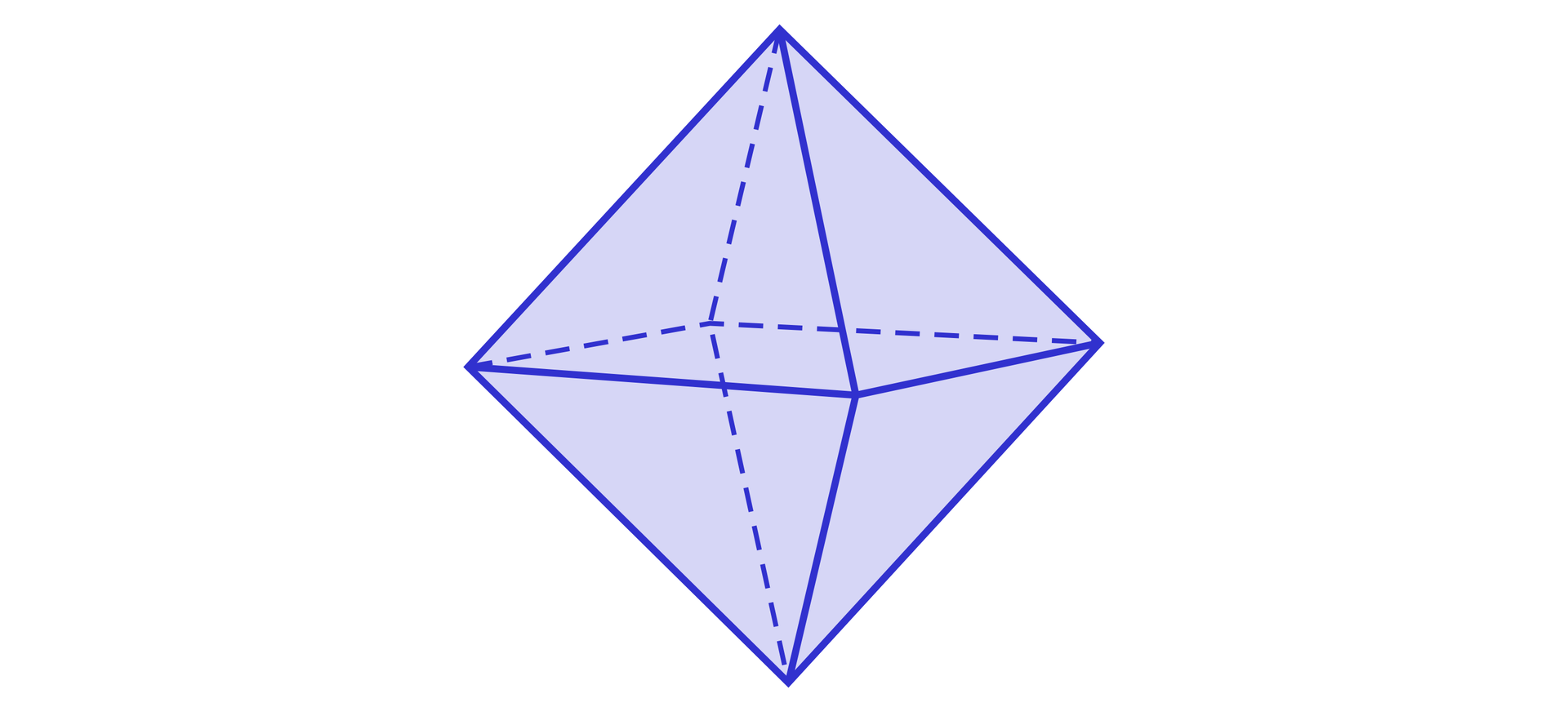
Z kolei ośmiościan jest przykładem wielościanu, który ma trzy przekątne i ani jednej przekątnej ściany.
Ciekawą grupę wielościanów stanowią wielościany foremnewielościany foremne. Wszystkie ściany są przystającymi wielokątami foremnymi i w każdym wierzchołku spotyka się taka sama liczba ścian. Istnieje tylko pięć takich brył. Są to: czworościan, sześcian, ośmiościan, dwunastościan i dwudziestościan.
Na bazie brył foremnych można tworzyć nowe bryły poprzez ścinanie ich wierzchołków. Przykładem takiego wielościanu jest czworościan ścięty, który powstał w wyniku odcięcia naroży czworościanu.

W podobny sposób możemy otrzymać sześcian ścięty – jest to sześcian z odciętymi wierzchołkami.
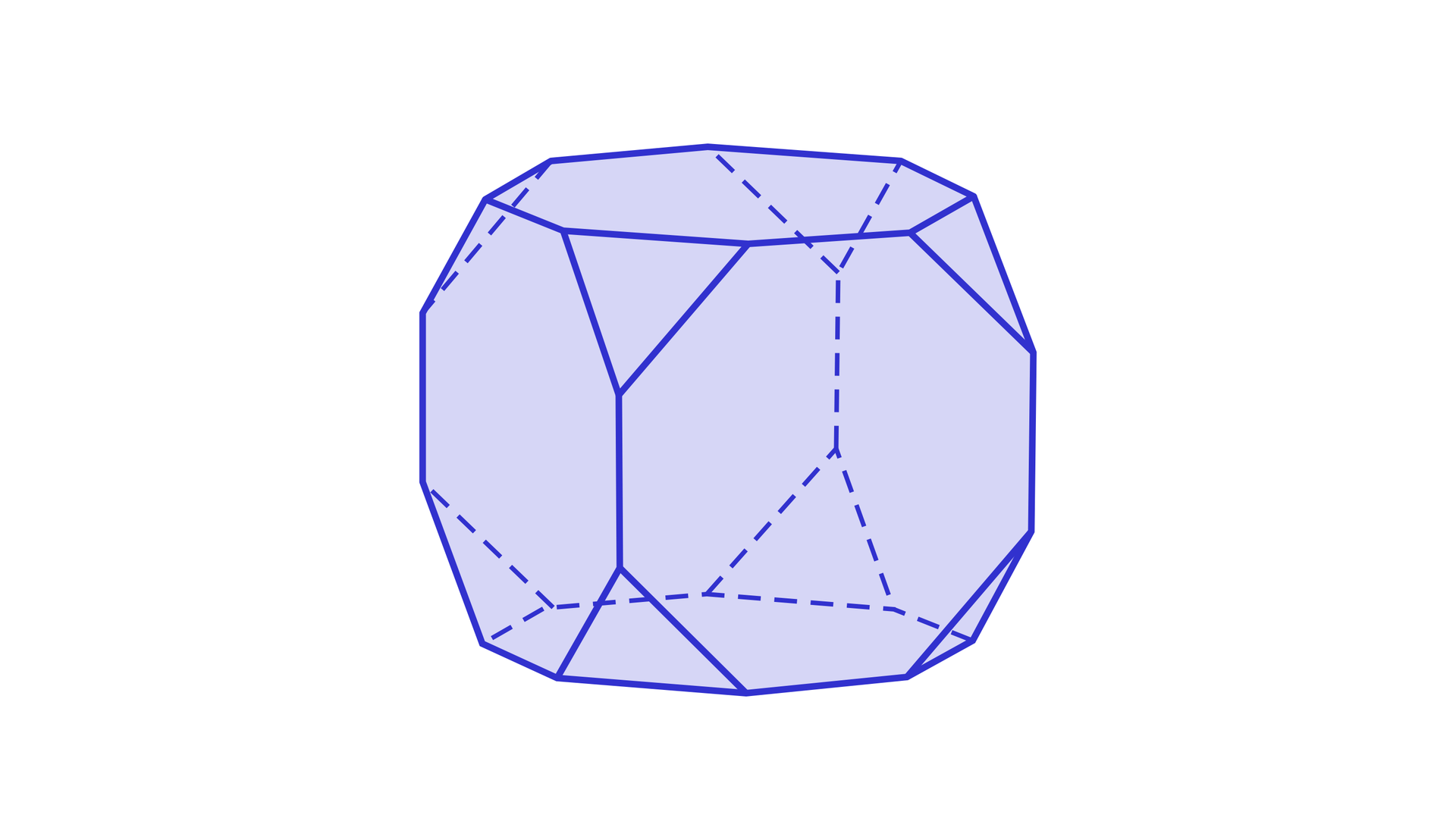
Niektóre wielościany mają ciekawą własność.
Jeżeli w sześcianie środki sąsiednich ścian połączymy odcinkami, otrzymamy ośmiościan.
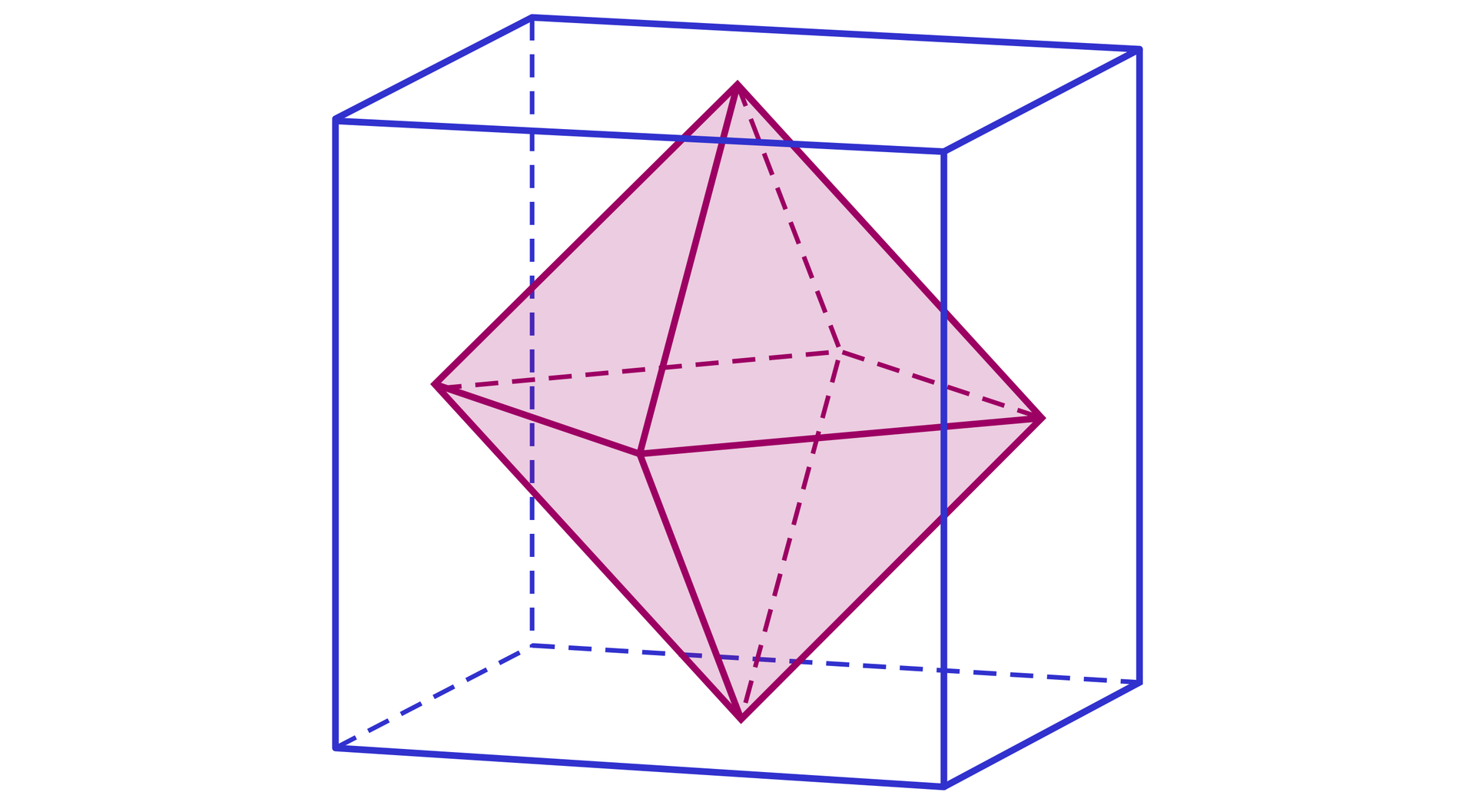
Gdy podobnie postąpimy w ośmiościanie foremnym, czyli połączymy odcinkami środki sąsiednich ścian, to w wyniku tej operacji otrzymamy sześcian.
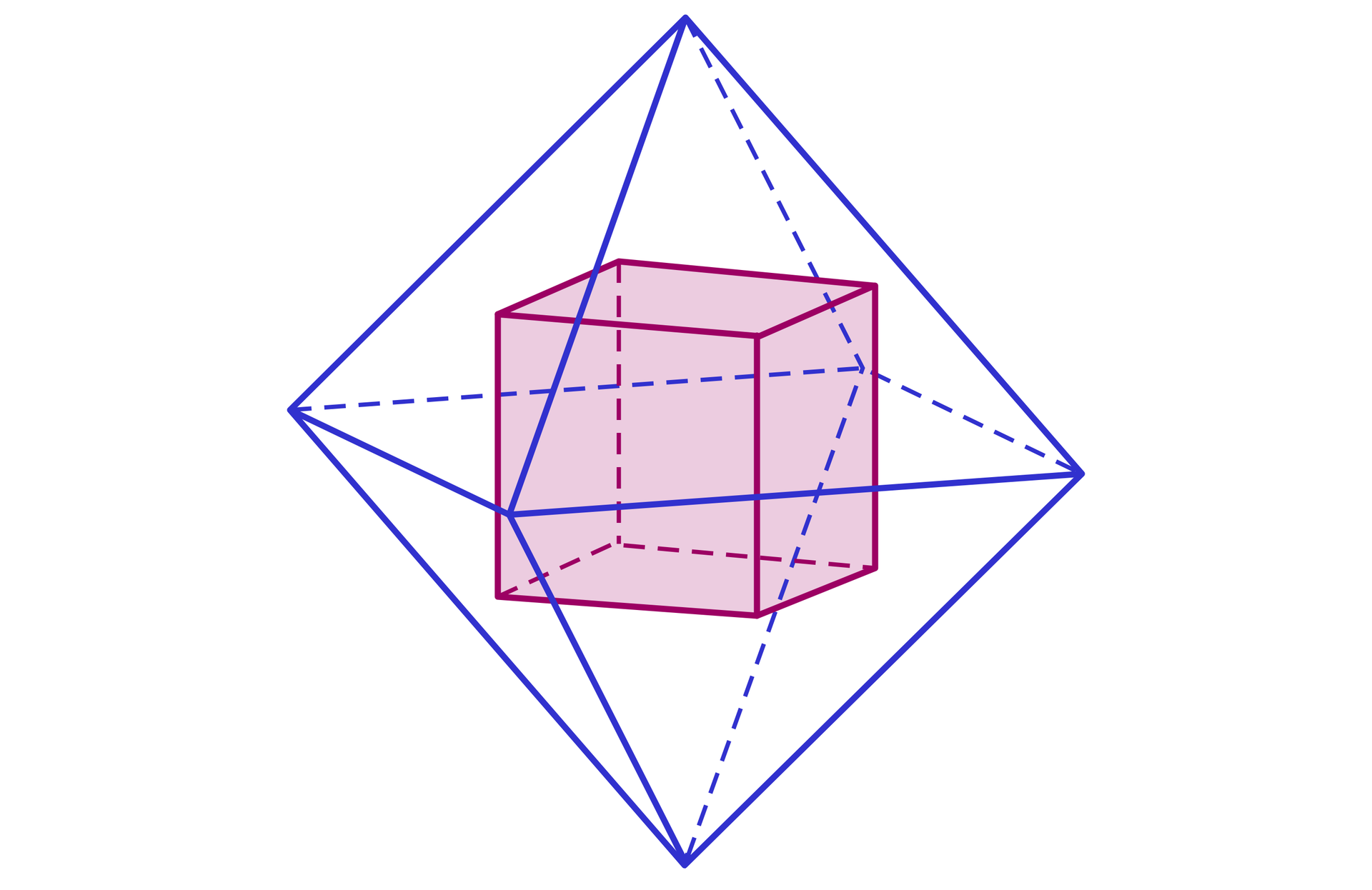
Wielościany o takiej własności nazywamy wielościanami dualnymi.
Słownik
bryła przestrzenna, której wszystkie ściany są wielokątami
wielościan, w którym dowolne dwa punkty tworzą odcinek zawierający się w całości w tej bryle
wielościan, w którym istnieje przynajmniej jeden odcinek utworzony przez dowolne punkty tej bryły, który nie zawiera się w całości w tym wielościanie
odcinek, który łączy dwa sąsiednie wierzchołki bryły
odcinek łączący dwa wierzchołki bryły, które nie sąsiadują ze sobą, zawierający się w ścianie (wieloboku)
odcinek, który łączy wierzchołki wielościanu i nie należy do żadnej ściany tej bryły
wielościany, których wszystkie ściany są przystającymi wielokątami foremnymi i w każdym wierzchołku spotyka się taka sama liczba ścian