Przeczytaj
Dotarcie do idealnego prawa gazowego
Ponad trzy stulecia temu naukowcy przeprowadzali eksperymenty, aby sprawdzić, jak zachowują się gazy, jeśli ich ciśnienie lub temperatura ulegną zmianie. Na podstawie badań sformułowano prawa dla hipotetycznego gazu, zwanego „gazem doskonałymgazem doskonałym”. Poniżej zapisano wnioski, które wynikają z tych praw.
Prawo Boyle’a
W r. zostało sformułowane prawo Boyle’a. Naukowiec Robert Boyle (czyt. boil) odkrył, że tak długo, jak temperatura gazu pozostaje stała, wzrost ciśnienia gazu powoduje zmniejszenie objętości gazu. Prawo zakłada, że ciśnienie gazu (w stałej temperaturze) jest odwrotnie proporcjonalne do jego objętości – określa się to mianem przemiany izotermicznejprzemiany izotermicznej. W formie matematycznej można to przedstawić jako:
Gdzie:
– ciśnienie;
– objętość;
– znak oznaczający „jest proporcjonalne do”.

Wykres funkcji ciśnienia od objętości nazywa się izotermąizotermą ().
Prawo Charles’a
Jacques Charles (czyt. szarl) zbadał zależność temperatury () gazu i jego objętości. Prawo sformułowane przez naukowca zakłada, że w izochorycznej przemianie stałej masy gazu doskonałego, jego ciśnienie () zależy wprost proporcjonalnie od temperatury bezwzględnejtemperatury bezwzględnej.

Wykres funkcji ciśnienia od czasu nazywa się izochorąizochorą ().
Prawo Gay‑Lussaca
Prawo sformułowane przez francuskiego chemika i fizyka Louisa Gay‑Lussaca mówi, że w trakcie przeprowadzania procesu izobarycznego, stosunek objętości do temperatury () jest stały – objętość () i temperatura są w tym procesie wielkościami proporcjonalnymi.

Wykres funkcji objętości od czasu nazywamy izobarąizobarą ().
Równanie Clapeyrona (równanie stanu gazu doskonałego)
jest kombinacją wszystkich omówionych praw gazowych:
Gdzie:
– ciśnienie gazu;
– objętość;
– liczba moli gazu;
– temperatura bezwzględna (w Kelwinach);
– stała gazowa; .
W obliczeniach należy zwrócić uwagę na warunki, w jakich znajduje się gaz (warunki standardowewarunki standardowe albo warunki normalnewarunki normalne).
Do przeliczenia temperatury () wyrażonej w stopniach Celsjusza () na Kelwiny (), należy posługiwać się zależnością:
Przeliczanie temperatury wyrażonej w stopniach Celsjusza na skalę Kelwina.
np. w skali Kelwina wynosi:
w skali Kelwina ma wartość .
Jak wyprowadzić prawa gazowe z równania stanu gazu doskonałego?
Mamy początkowe wartości dla stanu gazu:
W innych warunkach, kiedy zmieniamy stan gazu, liczba cząsteczek/atomów nie zmienia się w trakcie przemiany ().
Gdy ciśnienie gazu jest stałe (), otrzymujemy:
Dzielimy dwie strony równania przez i dotarliśmy do prawa Gay‑Lussaca:
Zastosowanie równania gazu doskonałego (równanie Clapeyrona)
Równanie Clapeyrona stosuje się w zadaniach praktycznych, gdy gaz zmienia swoją objętość, ciśnienie lub temperaturę. Pozwala ono obliczać te wielkości fizyczne w różnych przemianach gazowych. Przekształcając równanie Clapeyrona, możemy również wyznaczyć wielkości w stałych warunkach:
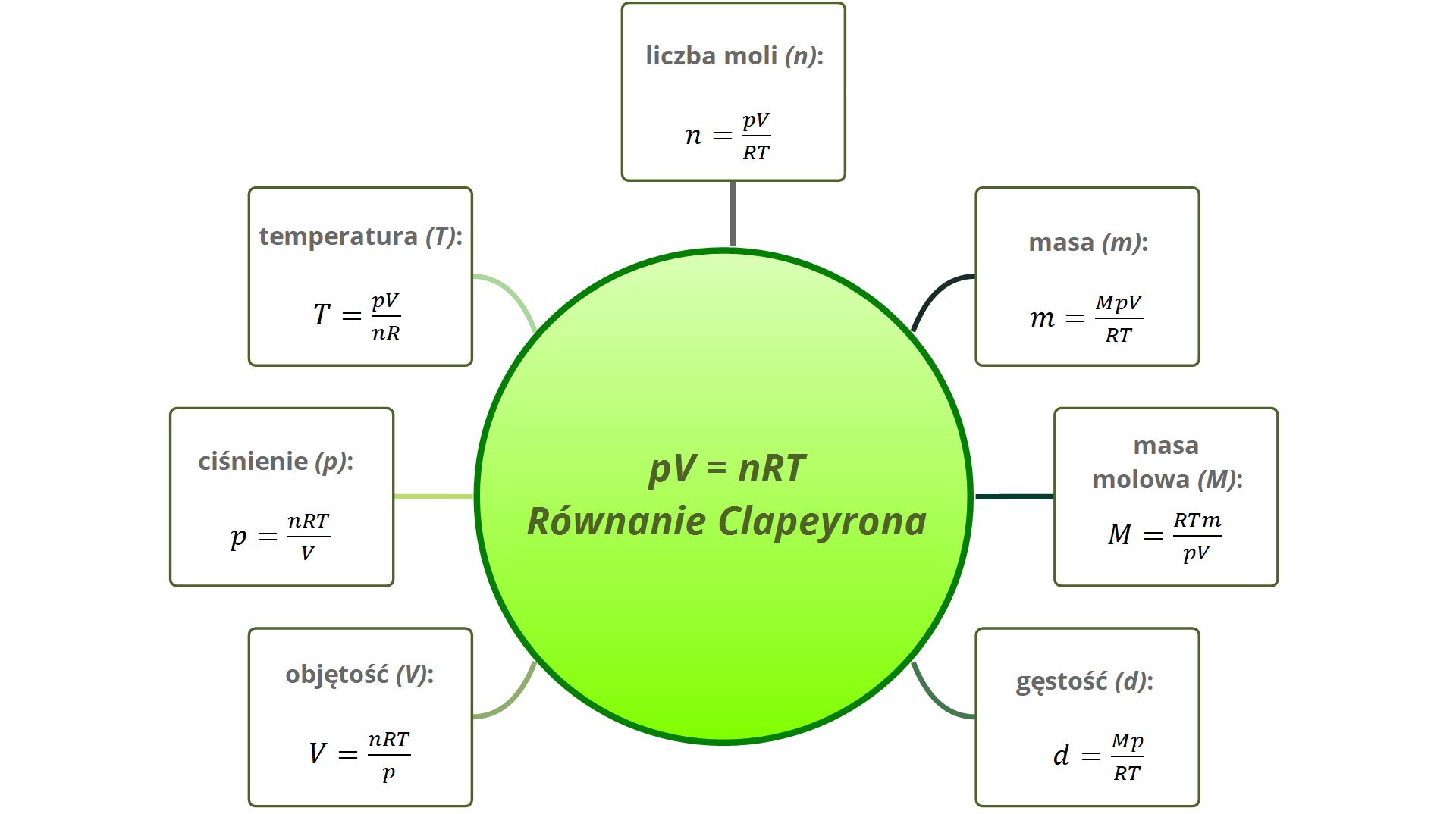
Spójrz na poniższe problemy, aby zapoznać się z różnymi przykładami zastosowań równania Clapeyrona. Najpierw spróbuj rozwiązać je samodzielnie, a jeśli potrzebujesz pomocy – rozwiązania są ukryte tuż pod nimi.
Oblicz ciśnienie, jakie jest wywierane na mole gazu znajdującego się w pojemniku o objętości , jeśli temperatura wewnątrz układu wynosi .
Oblicz masę chloru w temperaturze i pod ciśnieniem . Przyjmij, że stała gazowa wynosi .
Słownik
gaz idealny, przybliżony model gazu nieuwzględniający oddziaływań międzycząsteczkowych (wyjątkiem jest odpychanie w trakcie doskonale sprężystych zderzeń cząsteczek, które znajdują się w ciągłym chaotycznym ruchu). W stosunku do objętości gazu, objętości cząsteczek są znikome
(proces izotermiczny) proces termodynamiczny, podczas którego temperatura układu nie ulega zmianie
linia na wykresie termodynamicznym, która przedstawia proces izotermiczny
(proces izochoryczny) proces termodynamiczny, podczas którego objętość układu nie ulega zmianie
linia na wykresie termodynamicznym, która przedstawia proces izochoryczny
(proces izobaryczny) proces termodynamiczny, podczas którego ciśnienie nie ulega zmianie
linia na wykresie termodynamicznym, która przedstawia proces izobaryczny
stosowana niekiedy nazwa temperatury Kelvina, w której punktowi potrójnemu wody (trzy fazy wody są w równowadze termodynamicznej) przypisano wartość
(STP, ang. standard temperature and pressure) ściśle określona temperatura i ciśnienie otoczenia, które stanowią rodzaj punktu odniesienia dla pomiarów doświadczalnych i obliczeń fizykochemicznych. Według IUPAC: ciśnienie standardowe – , temperatura standardowa –
umownie przyjęte wartości ciśnienia (tzw. ciśnienie normalne), gdzie i temperatury (tzw. temperatura normalna), gdzie , dla których podaje się zwykle wartości wielkości fizycznych, charakteryzujące ciała
Bibliografia
Bielański A., Podstawy Chemii nieorganicznej, t. 1‑2, Warszawa 2010.
Encyklopedia PWN
Lichocka H., Historia Chemii. Repozytorium Centrum Otwartej nauki.
Pazdro K., Zbiór zadań z chemii dla szkół ponadgimnazjalnych, Warszawa 2003.
Atkins P., Jones L., Chemia ogólna. Cząsteczki, materia, reakcje, Warszawa 2004.
Hassa R., Mrzigod A., Mrzigod J., Sułkowski W., Chemia 1. Podręcznik i zbiór zadań w jednym, Warszawa 2003.
Usnalski W., Chemia w szkole średniej, Warszawa 1998.