Przeczytaj
PRZYPOMNIJ SOBIE
Rozwiązaniem układu równań liniowych z dwiema niewiadomymi nazywamy parę liczb spełniającą jednocześnie każde równanie danego układu równań.
Dany jest układ równań . Przedstawimy interpretację geometryczną tego układu. Sprawdzimy, czy posiada rozwiązanie.
Doprowadzamy pierwsze równanie do postaci kierunkowej.
Wybieramy przykładowe punkty, których współrzędne spełniają to równanie. Mogą to być punkty przecięcia wykresu z osiami układu współrzędnych.
Oś – punkt
Oś – punkt
Zajmiemy się teraz drugim równaniem.
W tym równaniu pojawia się wartość bezwzględna liczby .
Przypomnimy podstawowe informacje na temat wartości bezwzględnej.
Algebraicznie wartością bezwzględną liczby rzeczywistej nazywamy:
liczbę , jeśli liczba jest nieujemna;
liczbę przeciwną do , jeśli liczba jest ujemna.
Wartość bezwzględną liczby rzeczywistejWartość bezwzględną liczby rzeczywistej oznaczamy .
Powyższą definicję możemy zapisać za pomocą wzoru
A zatem wracając do równania mamy:
jeśli , to
i wtedy równanie przyjmuje postać:
jeśli , to
i wtedy równanie przyjmuje postać:
Teraz przekształcamy równania do postaci kierunkowej i wybieramy punkty przez które przechodzi wykres.
i
i
Wybierając współrzędną musimy pamiętać o warunkach dotyczących zmiennej .
– otrzymujemy punkt i – otrzymujemy punkt
– otrzymujemy punkt i – otrzymujemy punkt
Rysujemy wykresy obu równań i sprawdzamy, czy posiadają one punkty wspólne.

Wykresy równań oraz przecinają się w jednym punkcie o współrzędnych .
Jak zawsze, przy metodzie graficznej, musimy jeszcze sprawdzić poprawność rozwiązania.
Podstawiamy wartości do każdej ze stron każdego z równań układu.
Otrzymaliśmy tożsamości, a zatem para liczb jest rozwiązanie układu równańrozwiązanie układu równań
.
Rozwiążemy metodą graficzną układ równań .
Korzystając z definicji wartości bezwzględnej, przekształcamy pierwsze równanie, rozpatrując przypadki.
i
Wtedy równanie przyjmuje postać:
i
i
Wybieramy przykładowe punkty, których współrzędne spełniają te równania. (Mogą to być punkty przecięcia wykresu z osiami układu współrzędnych).
, i ,
Wykres drugiego równania jest prostą równoległą do osi .
Rysujemy wykresy obu równań i sprawdzamy, czy posiadają one punkty wspólne.

Wykresy przecinają się w dwóch punktach: oraz .
Sprawdzamy poprawność odczytanych rozwiązań.
Dla pary :
Dla pary :
A zatem układ równań ma dwa rozwiązania: oraz .
Rozwiążemy metodą graficzną układ równań .
Korzystając z definicji wartości bezwzględnej przekształcamy pierwsze równanie rozpatrując przypadki.
I przypadek – I ćwiartka układu współrzędnych
wtedy i równanie przyjmuje postać
Wybieramy pary, które należą do pierwszej ćwiartki układu współrzędnych i spełniają to równanie.
,
II przypadek – II ćwiartka układu współrzędnych
wtedy i równanie przyjmuje postać
Wybieramy pary, które należą do drugiej ćwiartki i spełniają to równanie.
,
III przypadek – III ćwiartka układu współrzędnych
wtedy i równanie przyjmuje postać
Wybieramy pary, które należą do trzeciej ćwiartki układu współrzędnych i spełniają to równanie.
,
IV przypadek – IV ćwiartka układu współrzędnych
wtedy i równanie przyjmuje postać
Wybieramy pary, które należą do czwartej ćwiartki układu współrzędnych i spełniają to równanie.
,

Zajmiemy się teraz drugim równaniem .
Rozpatrujemy przypadki wynikające z definicji wartości bezwzględnej liczby.
I przypadek:
wtedy i równanie przyjmuje postać .
Przekształcamy równanie:
Wybieramy pary liczb spełniające to równanie:
, ,
II przypadek:
wtedy i równanie przyjmuje postać .
Przekształcamy równanie:
Wybieramy pary liczb spełniające to równanie:
,
A więc wykres równania ma postać:
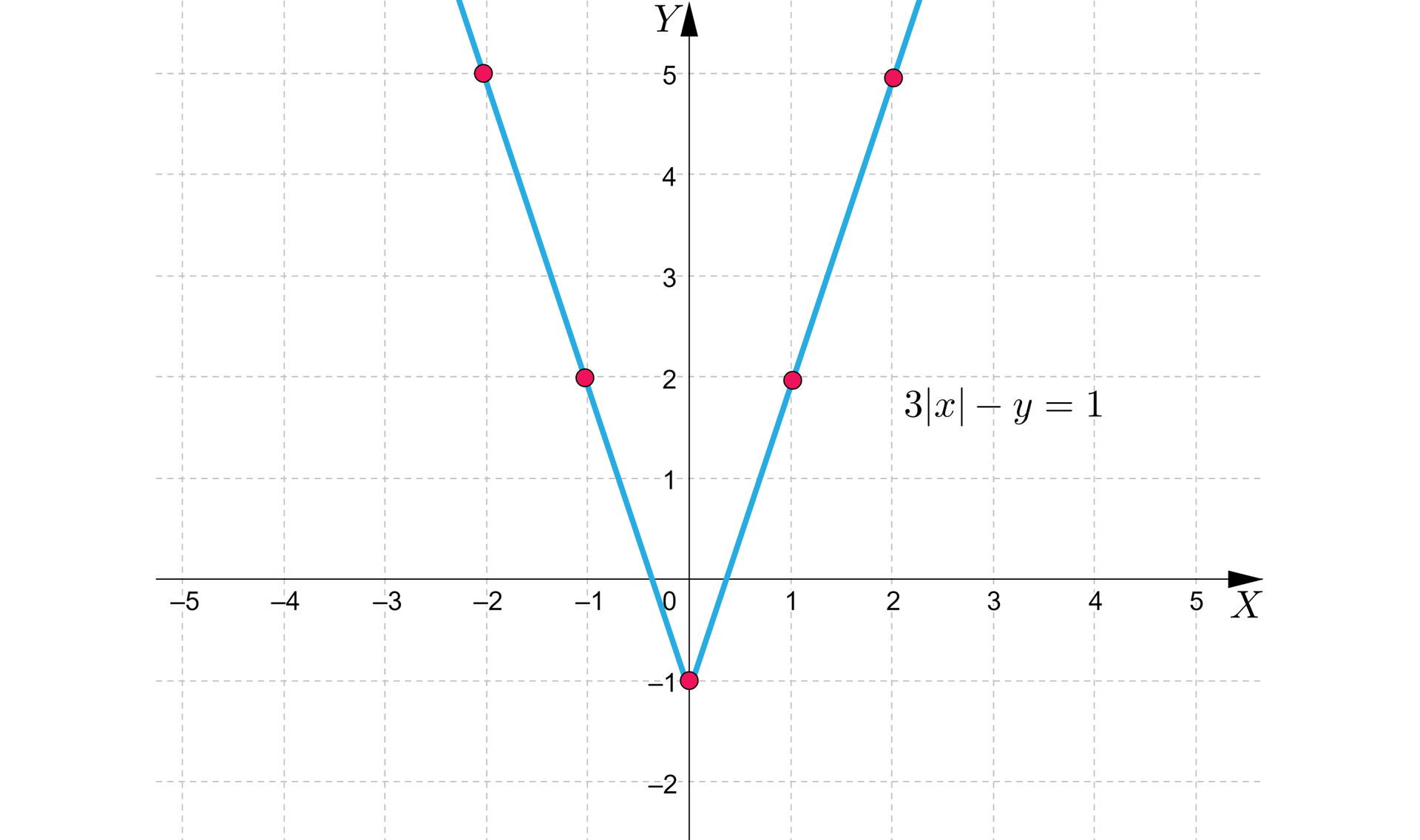
Umieszczamy powyższe wykresy w jednym układzie współrzędnych.
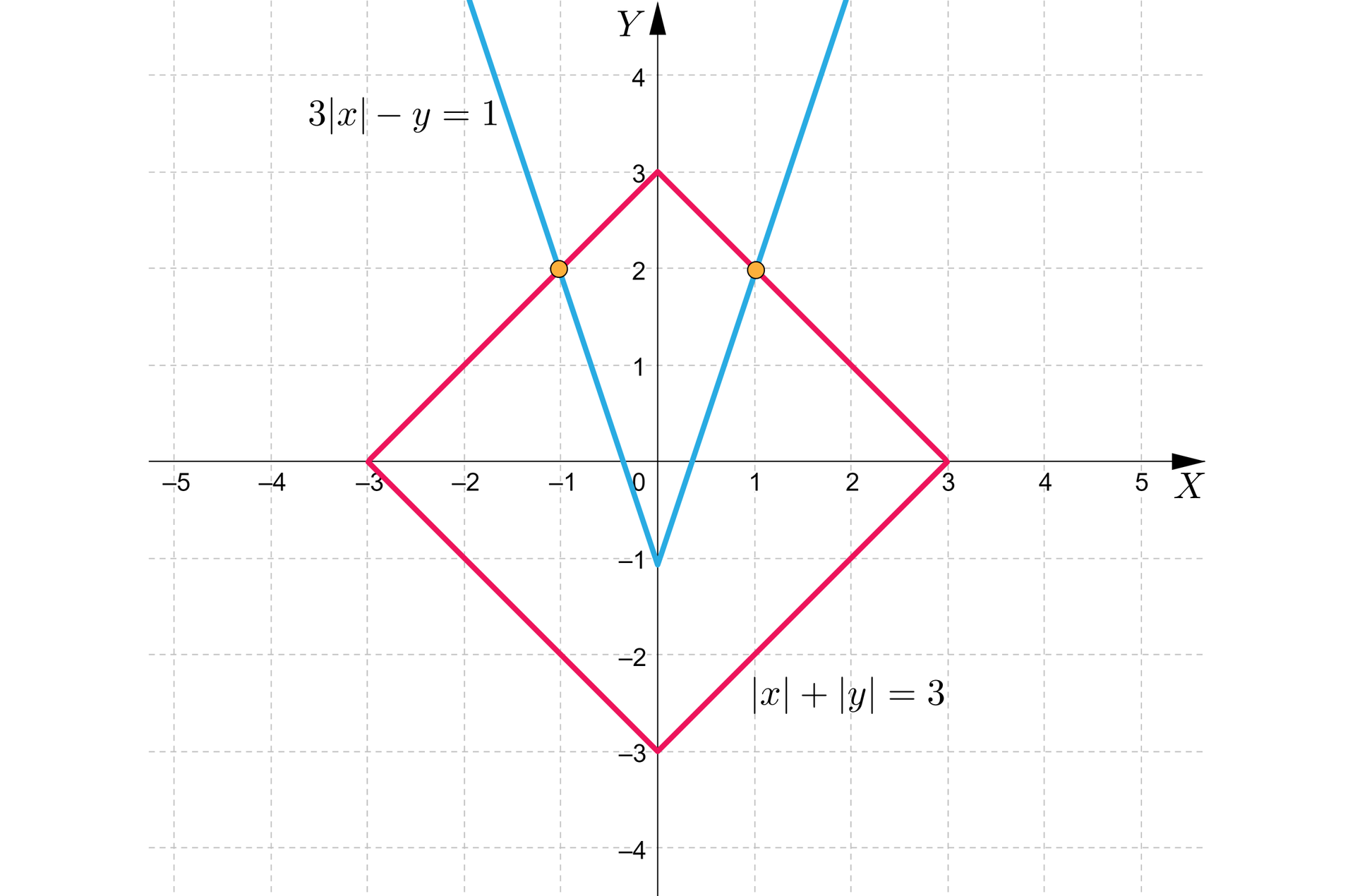
Wykresy przecinają się w dwóch punktach oraz .
Sprawdzamy poprawność odczytanych rozwiązań.
Dla pary :
Dla pary :
A zatem układ równań ma dwa rozwiązania: oraz .
Rozwiążemy metodą graficzną układ równań .
Doprowadzamy pierwsze równanie do postaci kierunkowej.
Wybieramy przykładowe punkty, których współrzędne spełniają to równanie. Mogą to być punkty przecięcia z osiami układu współrzędnych.
Oś – punkt
Oś – punkt
Rysujemy wykres równania .

Zajmiemy się teraz drugim równaniem .
Rozpatrujemy przypadki wynikające z definicji wartości bezwzględnej liczby.
I przypadek:
Wtedy równanie przyjmuje postać
.
Przekształcamy je do postaci kierunkowej i dobieramy pary liczb będące rozwiązaniem.
,
II przypadek:
Wtedy równanie przyjmuje postać
.
Przekształcamy je do postaci kierunkowej i dobieramy pary liczb będące rozwiązaniem.
,
Rysujemy wykres równania .

Umieszczamy wykresy obu równań w jednym układzie współrzędnych.

Wykresy przecinają się w dwóch punktach oraz .
Sprawdzamy poprawność odczytanych rozwiązań.
Dla pary :
Dla pary :
A zatem układ równań ma dwa rozwiązania: oraz .
Określimy liczbę rozwiązań układu równań w zależności od parametru .
Korzystając z przykładu , wiemy jaką postać będzie miał wykres równania .
Wyznaczymy jedynie punkty przecięcia wykresu z osiami i .
Oś – punkty ,
Oś – punkty ,
Rysujemy wykres.
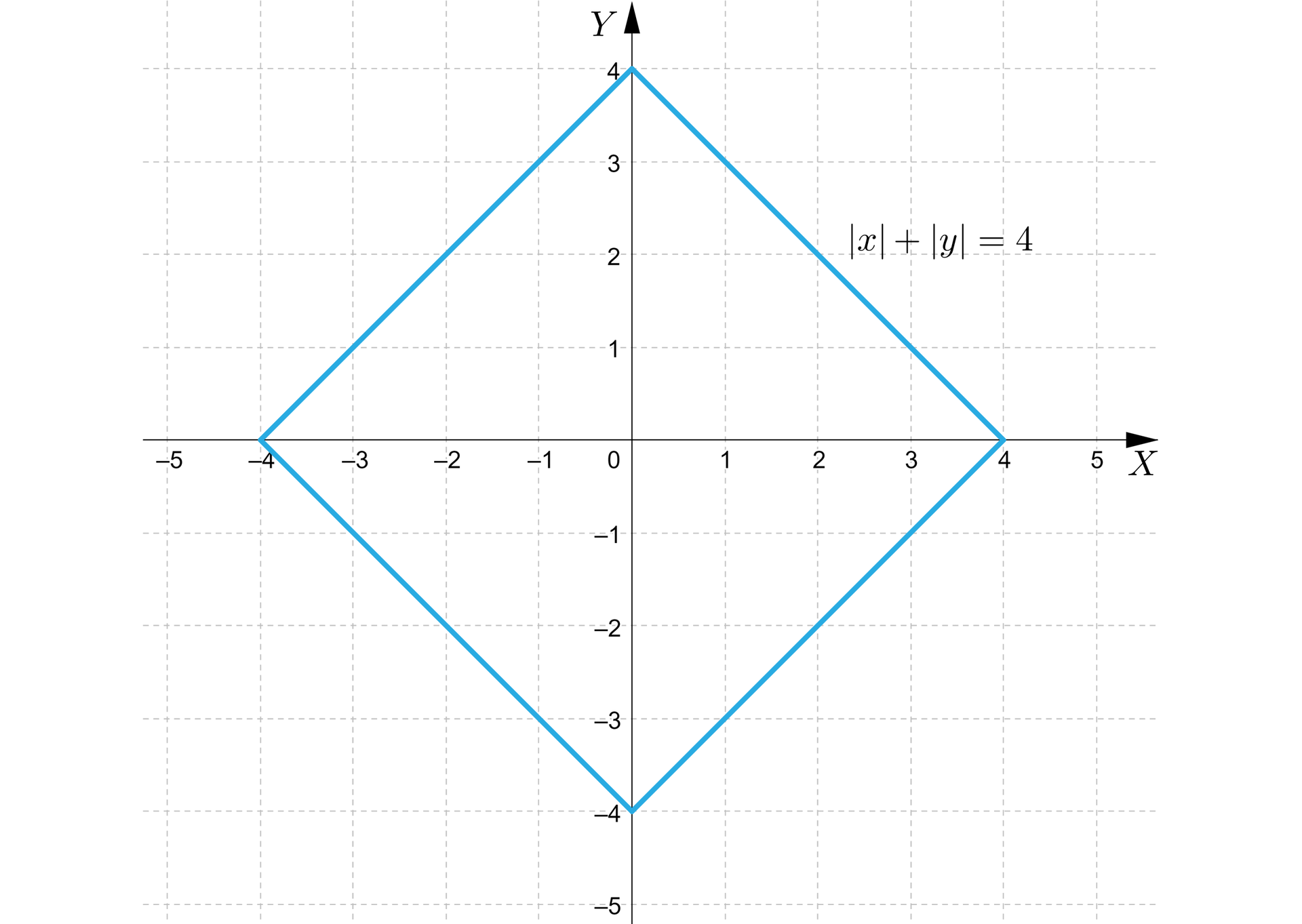
Rozpatrzymy teraz położenie wykresu równania w zależności od parametru .
Wykres jest prostą równoległą do osi , a parametr „przesuwa” tą prostą wzdłuż osi .
Przyjrzyjmy się następującym przypadkom:
Wtedy równanie przyjmuje postać .
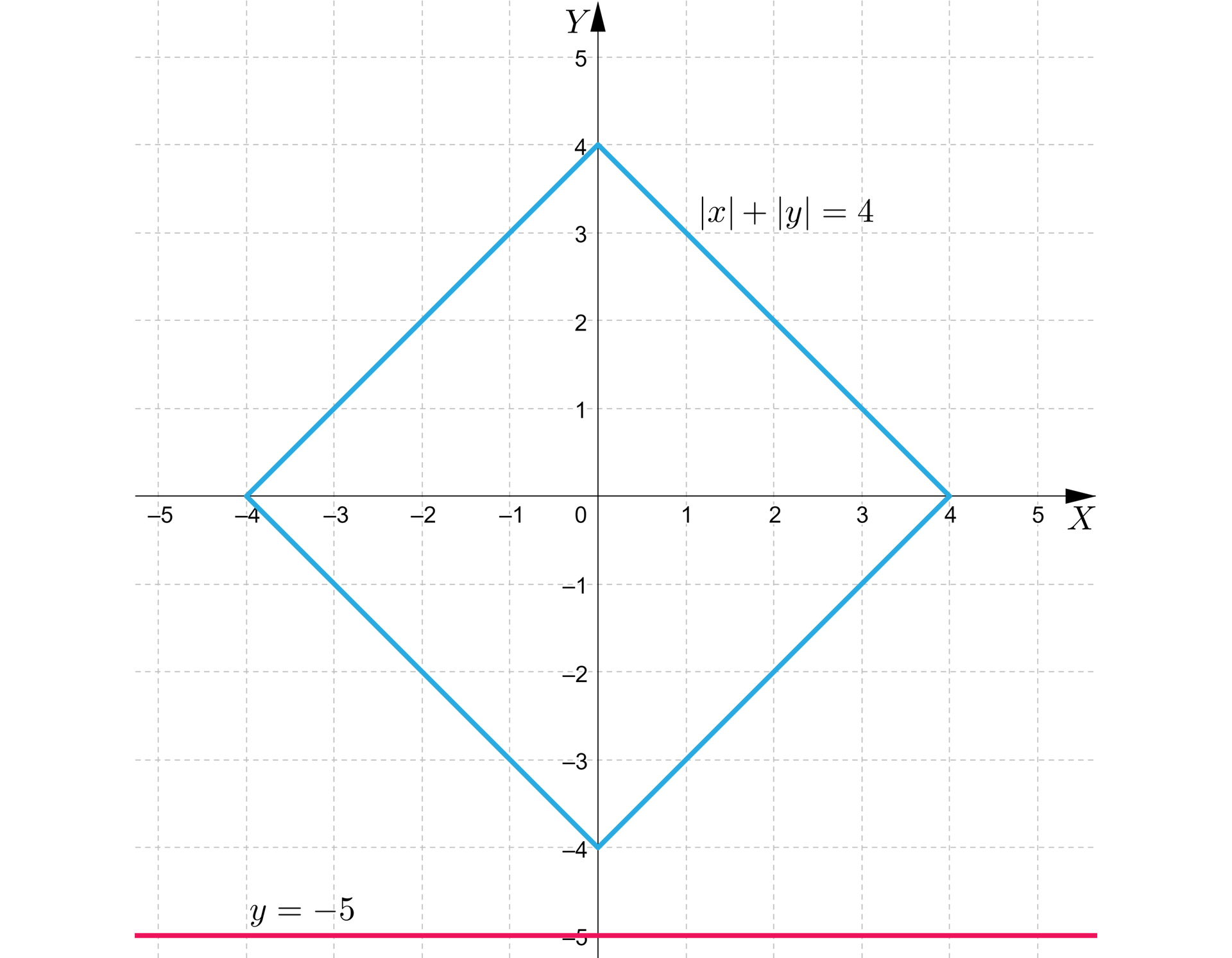
Wykresy nie mają teraz punktów wspólnych. Widać, że analogiczna sytuacja będzie dla wszystkich , np.:
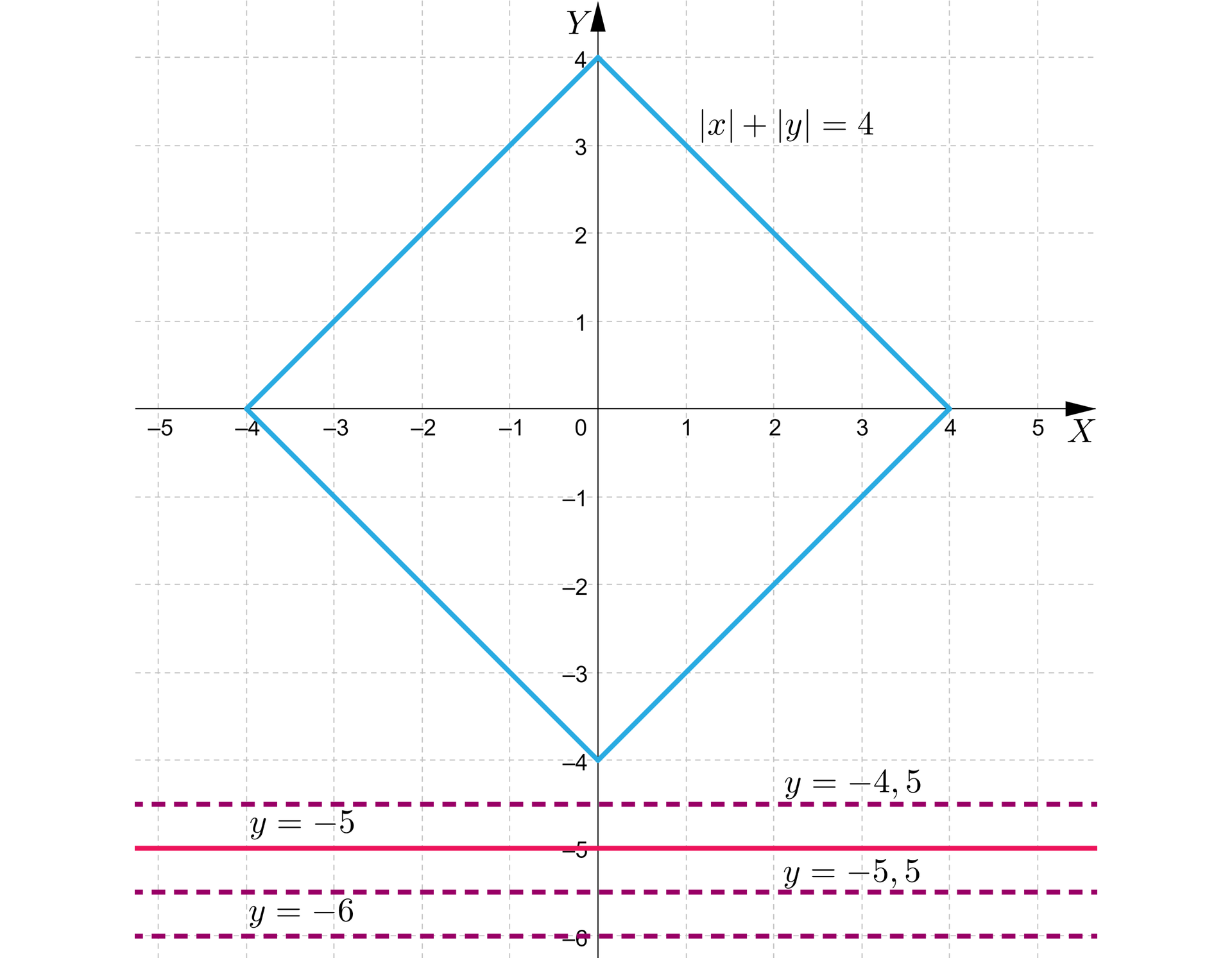
A także dla wszystkich , np.:

lub

Wykresy równań i oraz i mają jeden punkt wspólny.

Wykresy równań i mają dwa punkty wspólne.
Zauważmy, że analogiczna sytuacja będzie dla , np.:

Podsumowujmy nasze rozważania.
Układ równań :
nie ma rozwiązań dla ;
ma jedno rozwiązanie dla ;
ma dwa rozwiązania dla .
Słownik
para liczb spełniających każde z równań składowych w tym układzie