Przeczytaj
Siatka graniastosłupa prawidłowego trójkątnego to przedstawienie graniastosłupa na płaszczyźnie, powstające poprzez “rozcięcie” niektórych jego krawędzi tak, aby dało się rozłożyć ściany na płaszczyźnie.
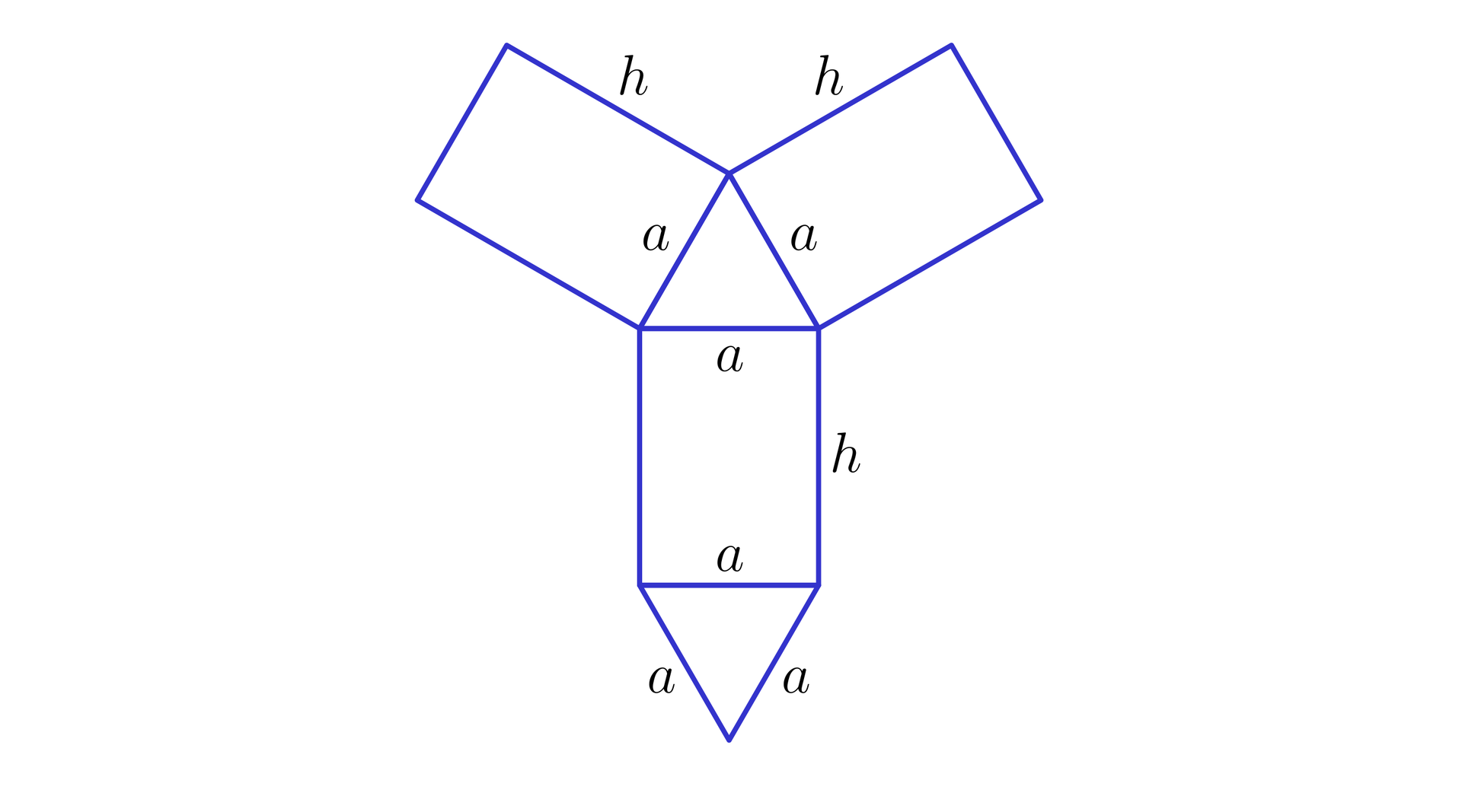
Z rysunku przedstawionego wyżej, możemy zauważyć, że siatka graniastosłupa prawidłowego trójkątnegograniastosłupa prawidłowego trójkątnego zbudowana jest z trzech przystających prostokątów (ścian bocznych graniastosłupa, siatka powierzchni bocznej graniastosłupa) o bokach długości i oraz dwóch przystających trójkątów równobocznych (podstawa górna i dolna graniastosłupa, siatka powierzchni podstaw) o boku długości .
Mrówka przeszła po powierzchni graniastosłupa prawidłowego trójkątnego z wierzchołka do wierzchołka , przy czym była to najkrótsza droga z przedstawionych na rysunku. Uzasadnimy, że drogą, którą wybrała mrówka jest (niebieska), jeżeli wiemy, że tangens nachylenia przekątnej ściany bocznej do krawędzi podstawy wynosi .

Rozwiązanie
Niech oznacza długość krawędzi podstawy oraz długość wysokości rozważanego graniastosłupa. Z warunków zadania wynika, że , stąd , czyli . Gdybyśmy “skleili” siatkę graniastosłupa z rysunku powyżej otrzymalibyśmy bryłę przedstawioną poniżej.

Obliczymy teraz kolejno długości dróg jakie mrówka mogła przejść.
1) Droga składa się z trzech odcinków. Jeden z nich równy jest wysokości graniastosłupa, a dwa pozostałe są równe wysokości podstawy graniastosłupa. Otrzymujemy zatem kolejno:
.
2) Droga składa się z trzech odcinków. Jeden z nich równy jest wysokości graniastosłupa, a dwa pozostałe są równe długości krawędzi podstawy graniastosłupa. Otrzymujemy zatem kolejno:
.
3) Droga składa się z dwóch odcinków. Jeden z nich równy przekątnej ściany bocznej graniastosłupa, a drugi długości krawędzi podstawy graniastosłupa. Otrzymujemy zatem kolejno:
.
Zatem .
W graniastosłupie prawidłowym trójkątnym , w którym pole ściany bocznej i podstawy są równe, połączono środki krawędzi podstaw w sposób pokazany na rysunku. Obliczymy ile razy pole powierzchni całkowitej powstałej bryły jest mniejsze od pola powierzchni całkowitej graniastosłupa .
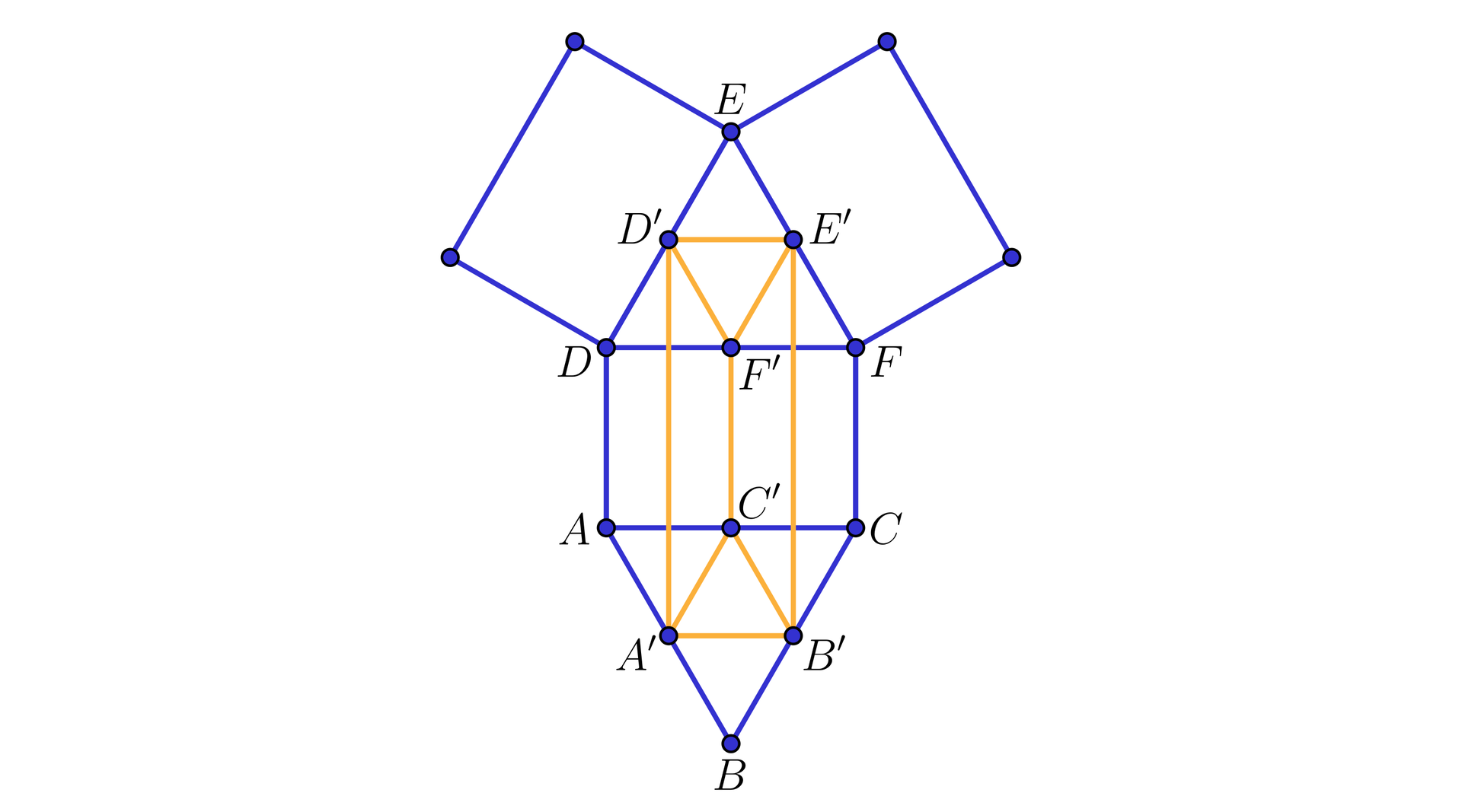
Rozwiązanie
Niech oznacza długość krawędzi podstawy oraz długość wysokości rozważanego graniastosłupa. Z warunków zadania wynika, że . Stąd otrzymujemy, że . W wyniku połączenia środków krawędzi podstaw w sposób pokazany na rysunku otrzymujemy graniastosłup prawidłowy trójkątny o krawędzi podstawy równej i wysokości równej wysokości graniastosłupa , czyli . Obliczymy pola powierzchni całkowitej obu graniastosłupów. Dla graniastosłupa otrzymujemy kolejno
.
Dla graniastosłupa otrzymujemy kolejno
.
Możemy policzyć ile razy pole powierzchni całkowitej graniastosłupa jest mniejsze od pola całkowitego graniastosłupa . Otrzymujemy
.
Czyli .
Obliczymy pole powierzchnipole powierzchni i objętość graniastosłupa prawidłowego trójkątnegoobjętość graniastosłupa prawidłowego trójkątnego, którego siatkę przedstawia rysunek.
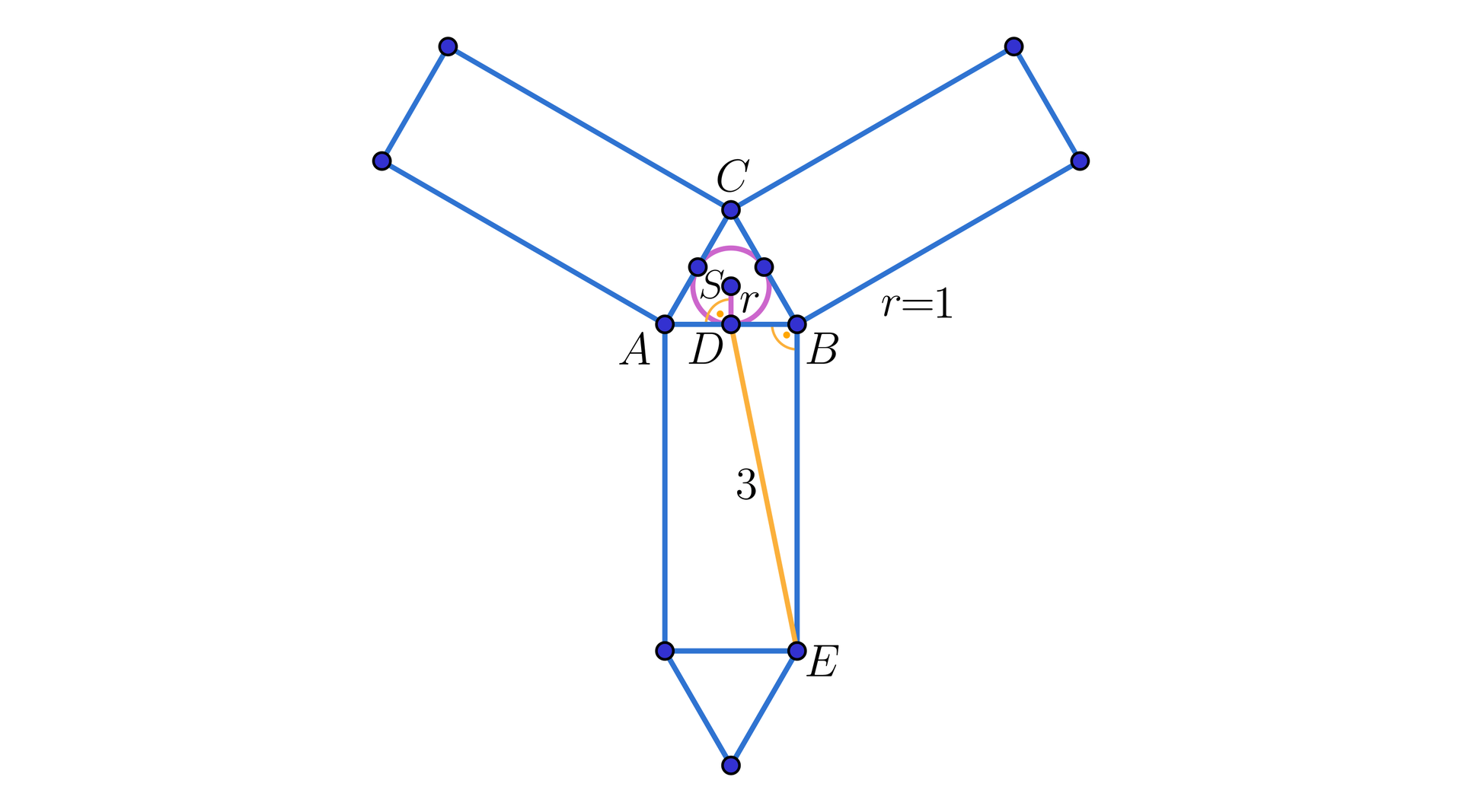
Rozwiązanie
Niech oznacza długość krawędzi podstawy oraz długość wysokości rozważanego graniastosłupa. Z warunków zadania wynika, że promień okręgu wpisanego w trójkąt równoboczny będący podstawą graniastosłupa jest równy . Korzystając z zależności, że promień okręgu wpisanego w trójkąt równoboczny jest równy wysokości tego trójkąta otrzymujemy kolejno
,
,
Punkt dzieli krawędź podstawy na połowę, zatem odcinek . Korzystając z twierdzenia Pitagorasatwierdzenia Pitagorasa dla trójkąta obliczymy wysokość graniastosłupa. Otrzymujemy
,
.
Możemy obliczyć pole powierzchni całkowitej i objętość naszego graniastosłupa
.
.
Wiadomo, że prostokąt przedstawiony na rysunku jest jedną, ze ścian bocznych graniastosłupa prawidłowego trójkątnego. Narysujemy jego siatkę oraz obliczymy pole powierzchni całkowitej tego graniastosłupa.
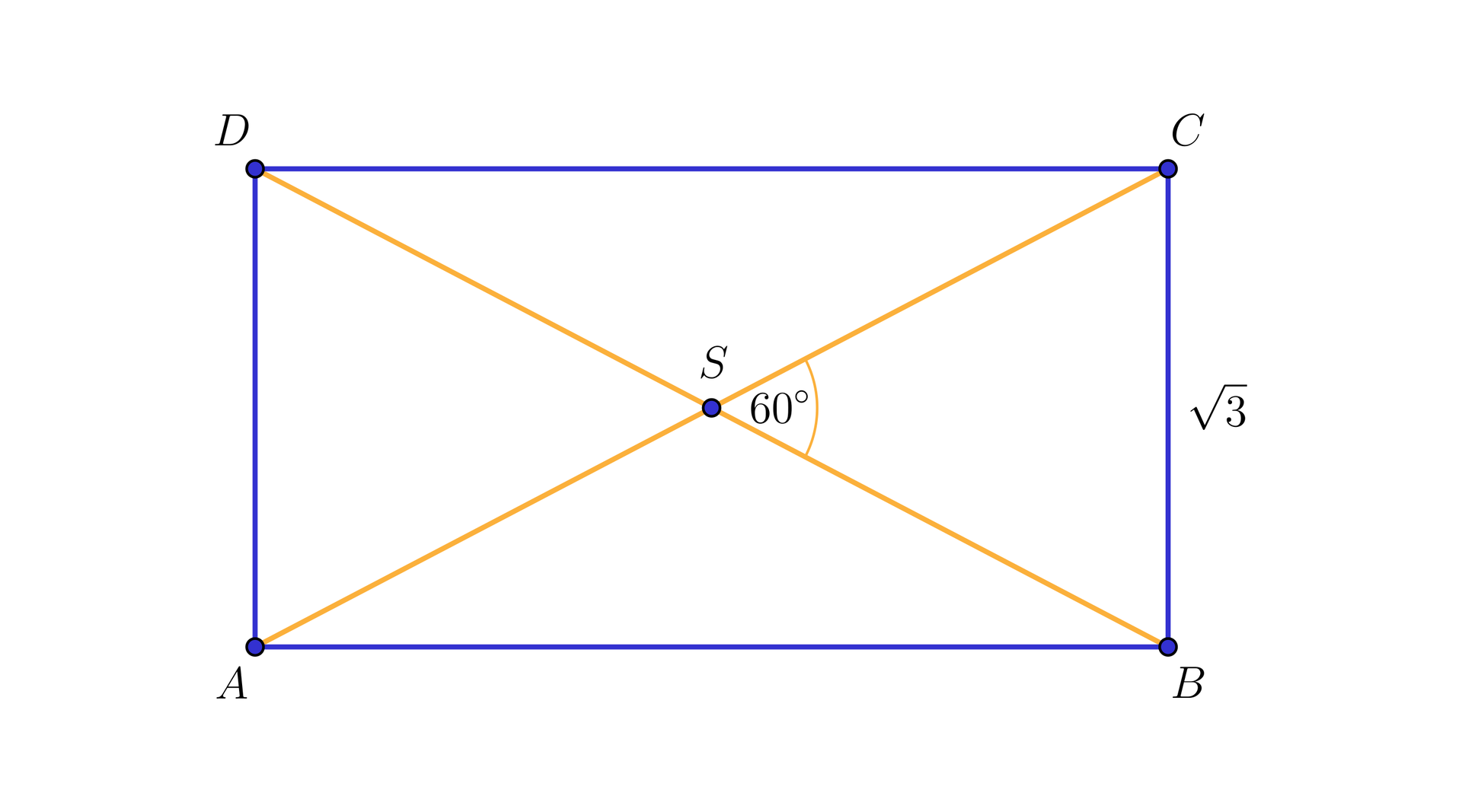
Rozwiązanie
Na początku wyznaczymy wymiary prostokąta . Z danych przedstawionych na rysunku wynika, że trójkąt jest równoboczny (odcinki i są równe, bo przekątne w prostokącie dzielą się na połowy). Zatem przekątna prostokąta jest równa . Korzystając z twierdzenia Pitagorasa możemy wyliczyć długość drugiego boku prostokąta. Otrzymujemy
,
.
Jest wiele możliwości narysowania siatek tego graniastosłupa. Natomiast istnieją dwa różne graniastosłupy w zależności od tego, który z boków danego prostokąta weźmiemy za wysokość, a który za krawędź podstawy. Zobaczmy kilka przykładowych siatek. Obliczymy pola powierzchni tych graniastosłupów.
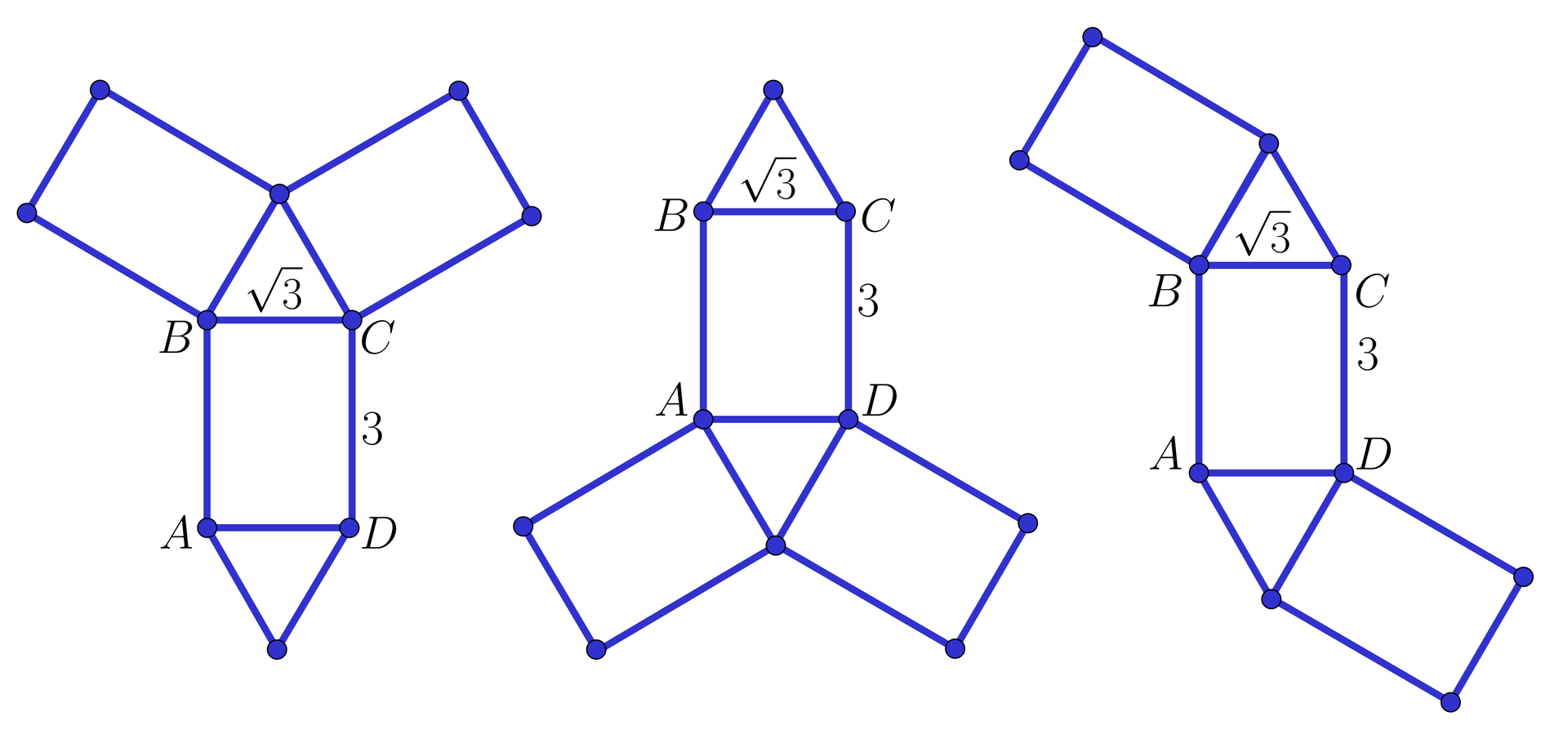
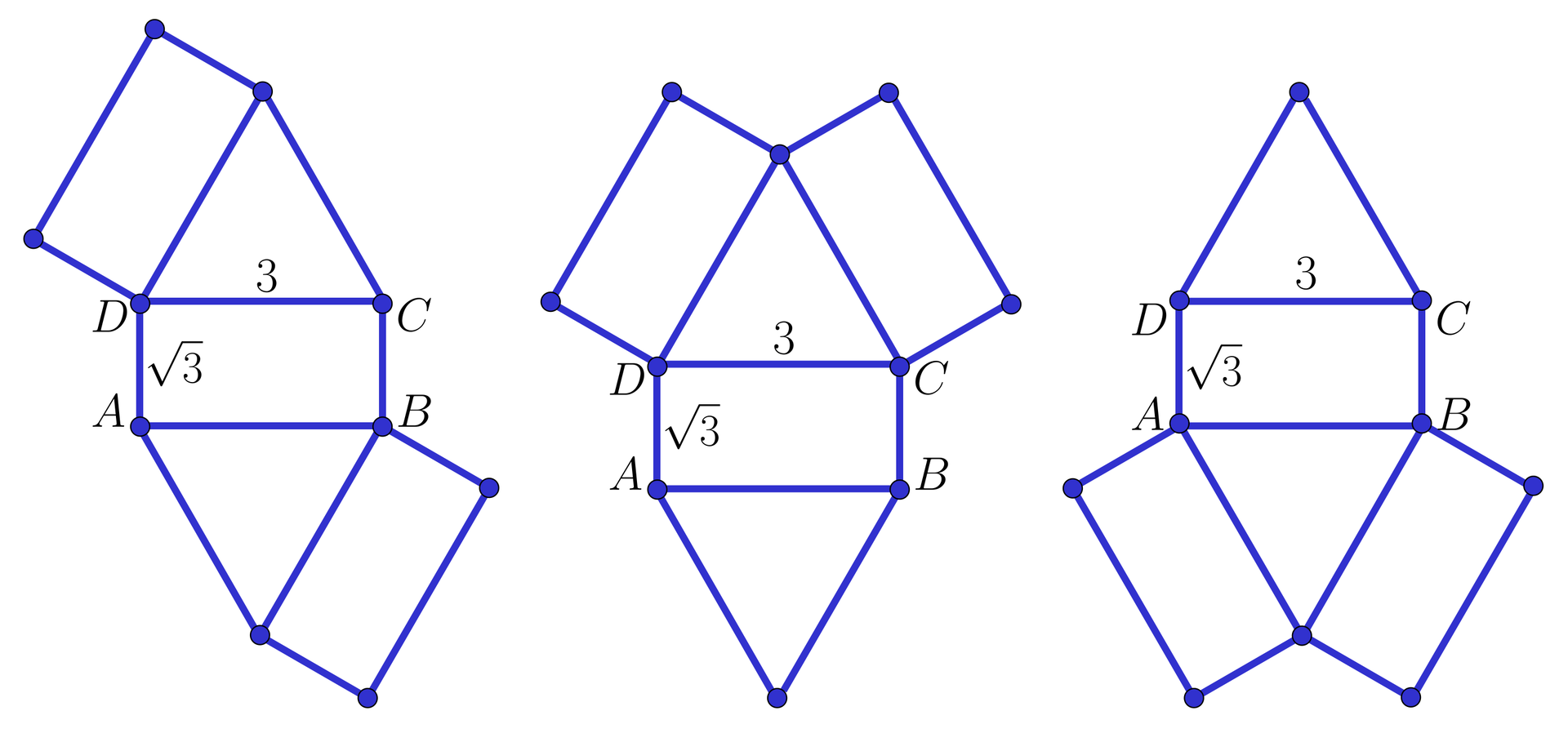
Dla pierwszego graniastosłupa krawędź podstawy jest równa oraz wysokość .
.
Dla graniastosłupa na drugim rysunku krawędź podstawy jest równa oraz wysokość .
.
Wskażemy, który z poniższych rysunków przedstawia siatkę z której można skleić graniastosłup prawidłowy trójkątny przedstawiony na rysunku poniżej.

-
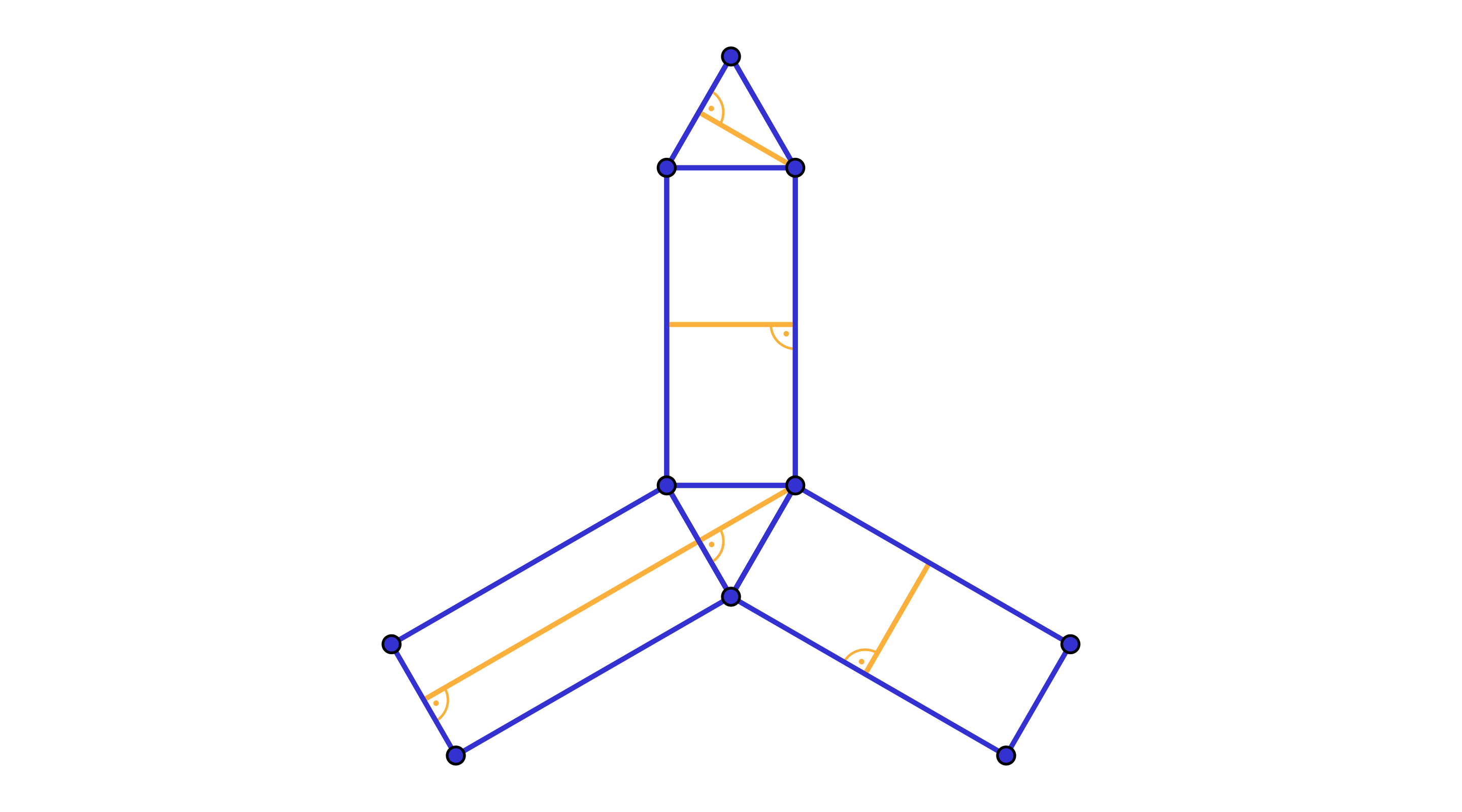
Rysunek 1
-
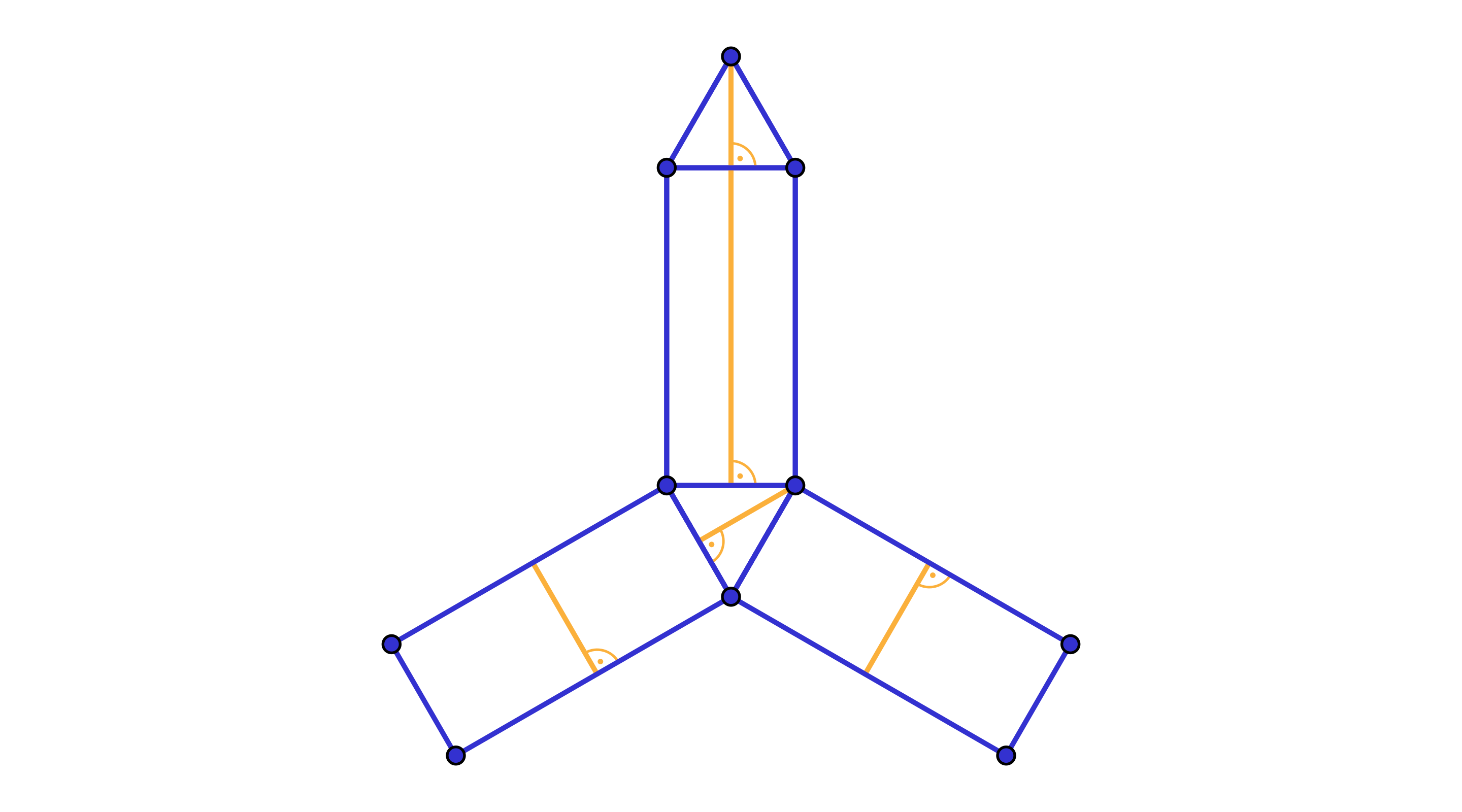
Rysunek 2
-
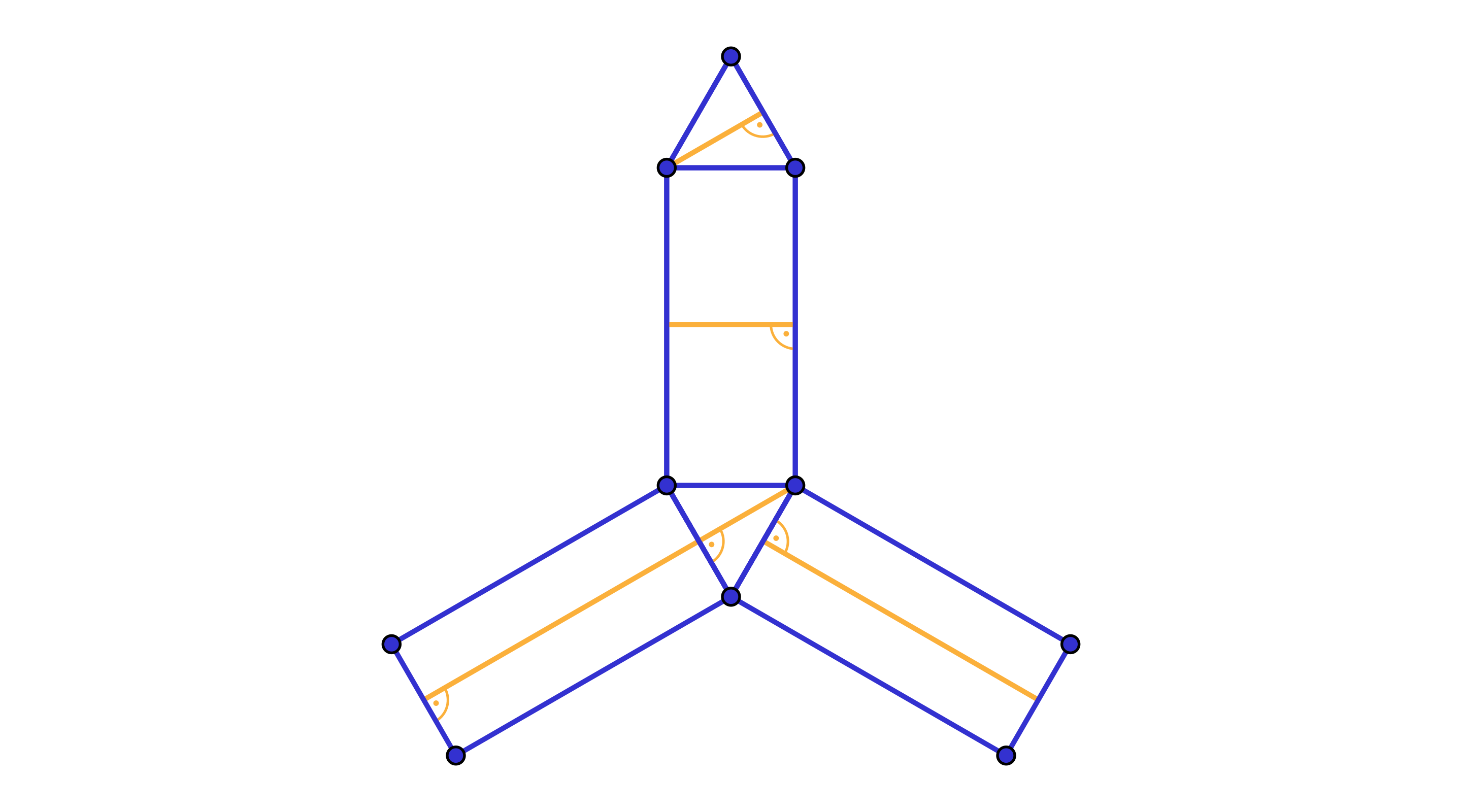
Rysunek 3
Rozwiązanie
Rysunek 1 przedstawia prawidłową siatkę. Po sklejeniu schemat odcinków na siatce odpowiada wyjściowemu schematowi odcinków na graniastosłupie.
Rysunek 2 nie przedstawia prawidłowej siatki. Po sklejeniu schemat odcinków na siatce nie odpowiada wyjściowemu schematowi odcinków na graniastosłupie.
Rysunek 3 nie przedstawia prawidłowej siatki. Po sklejeniu schemat odcinków na siatce nie odpowiada wyjściowemu schematowi odcinków na graniastosłupie.
Słownik
graniastosłup prosty, którego podstawą jest trójkąt równoboczny
w dowolnym trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej tego trójkąta
jest równa iloczynowi pola podstawy przez wysokość
definiujemy jako sumę pól jego podstaw (dwa trójkąty równoboczne) i pola powierzchni bocznej (trzy przystające prostokąty); pole powierzchni całkowitej graniastosłupa prawidłowego trójkątnego jest równe polu jego siatki