Najprostszymi dynamicznymi strukturami, które poznaliśmy, są stos i kolejka. Obydwie implementować można za pomocą różnych mechanizmów. Jedno z najprostszych rozwiązań, które służy zazwyczaj do wyjaśnienia działania tych struktur w języku Python, to użycie listy, jednej z wbudowanych struktur danych. Jest to struktura dynamiczna umożliwiająca zapisywanie dowolnej liczby elementów. Z jej pomocą można łatwo implementować operacje wykonywane na omawianych poniżej strukturach. Ponieważ jednak celem tego materiału jest wyjaśnienie zasad działania i implementowania struktur dynamicznych, wykorzystywane dalej listy skonstruujemy sami przy użyciu klas użytkownika.

Stos

Przypomnijmy, że stos to liniowa struktura typu LIFO (ang. Last‑In, First‑Out – ostatni na wejściu, pierwszy na wyjściu), która obsługuje dwie podstawowe operacje, tj. odkładanie i zdejmowanie danych. Dodatkowe działania, które wykonuje się na stosie, to odczytywanie wierzchołka stosu, czyli ostatniego odłożonego elementu, bez usuwania go, oraz ewentualnie sprawdzanie rozmiaru stosu, czyli liczby odłożonych elementów.

Biorąc powyższe warunki pod uwagę, do implementacji stosu wystarczy nam jednokierunkowa lista niecykliczna. Elementami tej listy będą węzły zawierające dane, np. liczby, oraz – w przypadku listy jednokierunkowej – referencjareferencjareferencja na element następny. Do zdefiniowania węzła użyjemy klasyklasaklasy zawierającej konstruktorkonstruktorkonstruktor inicjalizujący dwa pola klasy:

class Wezel:
    def __init__(self, liczba):
        self.liczba = liczba
        self.nastepny = None

Stworzenie nowego węzła i przypisanie wartości do jego składowych umożliwia instrukcja:

nowy = Wezel(liczba)

Stos zaimplementujemy również jako klasę, której atrybutem inicjalizowanym w konstruktorze referencją pustąreferencjareferencją pustą będzie referencja na wierzchołek stosu o nazwie wierzcholek.

class Stos:
    def __init__(self):
        self.wierzcholek = None

    # Poniżej dodamy kolejne metody

Do klasy Stos() dodamy teraz metody wykonujące charakterystyczne dla stosu operacje.

Zaczniemy od metody czyPusty(), która będzie zwracała wartość true (prawda), jeżeli stos będzie pusty, czyli w sytuacji, kiedy pole wierzcholek będzie referencją pustą. W przeciwnym razie metoda zwróci wartość false (fałsz).

def czy_pusty(self):
    if self.wierzcholek is None:
        print("Stos pusty!")
        return True
    return False

W celu zachowania poprawności działania struktury LIFO, funkcja odloz() będzie dodawała elementy na początku listy i odpowiednio funkcja zdejmij() będzie usuwała elementy również z początku listy.

Zacznijmy od metody odloz():

def odloz(self, liczba):
    print("Odkladam", liczba)
    nowy = Wezel(liczba)
    nowy.nastepny = self.wierzcholek
    self.wierzcholek = nowy

W funkcji odloz() tworzymy nowy węzeł i zapisujemy w nim wartość zmiennej liczba przekazaną jako argument. Następnie pole nastepny nowego elementu ustawiamy na dotychczasowy wierzcholek, w ten sposób dodajemy element na początku listy. Na koniec aktualizujemy pole wierzcholek, tak aby wskazywało na nowo dodany element.

Usuwanie pierwszego elementu jest możliwe dzięki referencji wierzcholek:

def zdejmij(self):
    if self.czy_pusty():
        return -sys.maxsize - 1

    pomocniczy = self.wierzcholek
    liczba = pomocniczy.liczba
    self.wierzcholek = self.wierzcholek.nastepny

    print("Zdejmuje", liczba)
    return liczba

Jeżeli stos jest pusty, tzn. zachodzi błąd niedopełnienia stosuniedopełnienie stosuniedopełnienia stosu, zwracamy minimalną wartość dla typu całkowitego, którą w języku wylicza się jako ujemną wartość maksymalną (-sys.maxsize) pomniejszoną o 1.

W przeciwnym razie dotychczasowy pierwszy element oraz zapisaną w nim wartość zapamiętujemy w zmiennych pomocniczych. Następnie ustawiamy wierzchołek na drugi element listy, dotychczasowy pierwszy usuwamy, a zapamiętaną wartość zwracamy.

Metoda pobierz_wierzcholek() ma tylko jedno zadanie: jeżeli stos nie jest pusty, zwraca wartość zapisaną w pierwszym, czyli ostatnim dodanym, elemencie listy:

def pobierz_wierzcholek(self):
    if self.czy_pusty():
        return -sys.maxsize - 1
    return self.wierzcholek.liczba

Metoda wypisz() posłuży do wypisania wartości odłożonych na stosie, czyli zapisanych w kolejnych węzłach listy:

def wypisz(self):
    if self.czy_pusty():
        return

    print("Stos zawiera:", end="")
    pomocniczy = self.wierzcholek
    while pomocniczy:
        print(pomocniczy.liczba, "", end="")
        pomocniczy = pomocniczy.nastepny;
    print()

Do wypisania wartości używamy pętli przechodzącej po wszystkich elementach stosu zapisywanych w zmiennej pomocniczy, którą ustawiamy na wierzchołek, a następnie wewnątrz pętli przesuwamy na kolejne węzły wskazywane przez pole nastepny. Pętla będzie działać dopóki nie dojdziemy do ostatniego węzła, którego referencja nastepny będzie pusta.

Do sprawdzenia działania stosu możemy użyć poniższego kodu:

stos = Stos()
stos.odloz(1)
stos.odloz(2)
stos.odloz(3)
stos.wypisz()
stos.zdejmij()
stos.zdejmij()
stos.zdejmij()
stos.zdejmij()

import sys

class Wezel:
    def __init__(self, liczba):
        self.liczba = liczba
        self.nastepny = None

class Stos:
    def __init__(self):
        self.wierzcholek = None

    def czy_pusty(self):
        if self.wierzcholek is None:
            print("Stos pusty!")
            return True
        return False

    def odloz(self, liczba):
        print("Odkladam", liczba)
        nowy = Wezel(liczba)
        nowy.nastepny = self.wierzcholek
        self.wierzcholek = nowy

    def zdejmij(self):
        if self.czy_pusty():
            return -sys.maxsize - 1
        pomocniczy = self.wierzcholek
        liczba = pomocniczy.liczba
        self.wierzcholek = self.wierzcholek.nastepny
        print("Zdejmuje", liczba)
        return liczba

    def pobierz_wierzcholek(self):
        if self.czy_pusty():
            return -sys.maxsize - 1
        return self.wierzcholek.liczba

    def wypisz(self):
        if self.czy_pusty():
            return

        print("Stos zawiera: ", end="")
        pomocniczy = self.wierzcholek
        while pomocniczy:
            print(pomocniczy.liczba, "", end="")
            pomocniczy = pomocniczy.nastepny;
        print()


stos = Stos()
stos.odloz(1)
stos.odloz(2)
stos.odloz(3)
stos.wypisz()
stos.zdejmij()
stos.zdejmij()
stos.zdejmij()
stos.zdejmij()

Odkladam 1
Odkladam 2
Odkladam 3
Stos zawiera: 3 2 1 
Zdejmuje 3
Zdejmuje 2
Zdejmuje 1
Stos pusty!

Kolejka

Kolejka to liniowa struktura danych typu FIFO (ang. First‑In, First‑Out – pierwszy na wejściu, pierwszy na wyjściu), co oznacza, że jej elementy odczytywane są zgodnie z kolejnością dodawania, a zatem odwrotnie niż w przypadku stosu.

W implementacji kolejki również użyjemy listy jednokierunkowej i takiej samej jak w przypadku stosu definicji klasy Wezel. Natomiast klasa Kolejka będzie zawierała dwa pola:

• glowa – referencję na pierwszy element kolejki;

• ogon – referencję na ostatni element kolejki, który ułatwi dodawanie elementów na końcu listy.

Nazwy pozostałych metod dostosujemy do omawianej struktury.

class Wezel:
    def __init__(self, liczba):
        self.liczba = liczba
        self.nastepny = None

class Kolejka:
    def __init__(self):
        self.glowa = None
        self.ogon = None

    # Poniżej dodamy kolejne metody

Metoda czy_pusta() działa tak samo, jak w przypadku stosu i każdej listy, tzn. jeżeli referencja na pierwszy element jest pusta, lista jest pusta.

    def czy_pusta(self):
        return self.glowa is None

Metoda dodaj() będzie dodawała nowe elementy na końcu listy przy użyciu pola ogon.

    def dodaj(self, liczba):
        print("Dodaje:", liczba)
        nowy = Wezel(liczba)

        if self.czy_pusta():
            self.glowa = self.ogon = nowy
        else:
            self.ogon.nastepny = nowy
            self.ogon = nowy

Na początku metody tworzymy nowy węzeł, przypisujemy otrzymaną liczbę do jego pola liczba, a referencję nastepny ustawiamy na wartość pustą. Następnie, jeżeli lista jest pusta, referencje na pierwszy (glowa) i ostatni (ogon) element listy ustawiamy na nowy węzeł.

W przeciwnym razie referencję nastepny dotychczasowego ostatniego elementu ustawiamy na nowy węzeł i aktualizujemy referencję ogon, aby wskazywał nowo dodany element.

Metoda usun() będzie zwracała kolejne elementy z początku listy, czyli działać będzie tak samo, jak metoda zdejmij() w przypadku stosu. Ponieważ jednak elementy będą dodawane na końcu listy, zasada działania kolejki FIFO zostanie zachowana.

def usun(self):
    if self.czy_pusta():
        return -sys.maxsize - 1

    pomocniczy = self.glowa
    liczba = pomocniczy.liczba
    self.glowa = self.glowa.nastepny
    print("Usuwam:", liczba)
    return liczba

import sys

class Wezel:
    def __init__(self, liczba):
        self.liczba = liczba
        self.nastepny = None

class Kolejka:
    def __init__(self):
        self.glowa = None
        self.ogon = None

    def czy_pusta(self):
        return self.glowa is None

    def dodaj(self, liczba):
        print("Dodaje:", liczba)
        nowy = Wezel(liczba)

        if self.czy_pusta():
            self.glowa = self.ogon = nowy
        else:
            self.ogon.nastepny = nowy
            self.ogon = nowy

    def usun(self):
        if self.czy_pusta():
            return -sys.maxsize - 1

        pomocniczy = self.glowa
        liczba = pomocniczy.liczba
        self.glowa = self.glowa.nastepny
        print("Usuwam:", liczba)
        return liczba

    def wypisz(self):
        if self.czy_pusta():
            print("Kolejka jest pusta!")
            return

        print("Kolejka zawiera: ", end="")
        pomocniczy = self.glowa
        while pomocniczy:
            print(pomocniczy.liczba, "", end="")
            pomocniczy = pomocniczy.nastepny
        print()


kolejka = Kolejka()
kolejka.dodaj(1)
kolejka.dodaj(2)
kolejka.dodaj(3)
kolejka.wypisz()
kolejka.usun()
kolejka.usun()
kolejka.usun()
kolejka.usun()

Dodaje: 1
Dodaje: 2
Dodaje: 3
Kolejka zawiera: 1 2 3 
Usuwam: 1
Usuwam: 2
Usuwam: 3

Lista

Przypomnijmy, że lista – podobnie jak stos i kolejka – jest liniową i dynamiczną strukturą danych. Elementami listy, jak już wiemy, są węzły, które zawierają dane oraz referencjęreferencjareferencję na element następny (w przypadku listy jednokierunkowej) lub na następny i poprzedni (w przypadku listy dwukierunkowej).

Do implementacji stosu i kolejki użyliśmy listy jednokierunkowej. Jej węzły zdefiniowaliśmy przy użyciu klasyklasaklasy zawierającej konstruktor argumentowy inicjalizujący dwa pola:

class Wezel:
    def __init__(self, liczba):
        self.liczba = liczba
        self.nastepny = None

Konstruktor wymaga podania argumentu podczas tworzenia obiektu, co pozwala zainicjować pole liczba otrzymaną wartością:

wezel = Wezel(1)

Lista jednokierunkowa

Listę jednokierunkową implementujemy jako klasęklasaklasę z jednym polem glowa – referencją na pierwszy element listy. Oprócz tego w klasie definiujemy metody umożliwiające dodawanie, usuwanie i wypisywanie elementów listy. W konstruktorze __init__() inicjalizujemy pole glowa referencją pustąreferencjareferencją pustą.

class Lista:
    def __init__(self):
        self.glowa = None

    # Poniżej dodamy kolejne metody

Metody czy_pusta() oraz wypisz() działają tak samo jak w przypadku stosu i kolejki. Poniżej wyjaśnimy działanie metody dodającej węzły na końcu listy oraz usuwającej węzły o podanej pozycji.

Dodawanie węzłów na końcu listy jednokierunkowej

Metoda dodaj() jako argument będzie przyjmowała liczbę całkowitą. Nowy węzeł – inaczej niż w przypadku stosu i kolejki – będzie dodawany na końcu listy.

def dodaj(self, liczba):
    print("Dodaję:", liczba)

    # Tworzymy nowy węzeł
    nowy = Wezel(liczba)

    # Jeżeli lista jest pusta
    if self.czy_pusta():
        self.glowa = nowy
        return

    # W przeciwnym razie przejdź do ostatniego elementu
    pomocniczy = self.glowa
    while pomocniczy.nastepny != None:
        pomocniczy = pomocniczy.nastepny

    # Dodajemy nowy węzeł na końcu listy
    pomocniczy.nastepny = nowy

Na początku metody tworzymy nowy węzeł, przekazując do jego konstruktora otrzymaną liczbę. Następnie, jeżeli lista jest pusta, nowy węzeł staje się pierwszym elementem listy przypisanym do pola glowa.

W przeciwnym razie za pomocą węzła pomocniczy w pętli przechodzimy listę do ostatniego elementu, którego referencja nastepny będzie pusta. Po zakończeniu pętli pole nastepny dotychczasowego ostatniego elementu ustawiamy na nowy węzeł. W ten sposób dodajemy węzeł na końcu listy.

R1eSTXiWk4HIn

Ilustracja przedstawia schemat dodawania węzła do końca listy jednokierunkowej. Lista składa się z czterech elementów, gdzie element pierwszy jest głową, trzeci jest pomocniczy, a czwarty jest elementem nowym. Elementy połączone są strzałkami z podpisem następny. Przy czym element NULL znajdujący się po elemencie trzecim został skreślony, a nowy element NULL jest następny po nowym elemencie czwartym.

Usuwanie węzłów z listy jednokierunkowej

Metoda usuwająca węzły z listy otrzymywać będzie jako argument liczbę całkowitą wskazującą indeks czy też numer węzła, który chcemy usunąć. Przyjmijmy, że indeksy węzłów zaczynają się od 1.

def usun(self, indeks):
    if self.czy_pusta():
        return

    print("Usuwam pozycje:", indeks)

    pomocniczy1, pomocniczy2 = self.glowa, None
    rozmiar = 0

    # Zliczamy elementy listy
    while pomocniczy1 != None:
        pomocniczy1 = pomocniczy1.nastepny
        rozmiar += 1

    # Jeżeli indeks jest większy od rozmiaru listy
    if indeks > rozmiar:
        print("Indeks poza zakresem.")
        return

    # Poniżej dodamy kod usuwający elementy

Jeżeli lista nie jest pusta, definiujemy zmienne, których używamy w metodzie:

• referencję pomocniczy1 ustawiamy na pierwszy element listy,

• referencję pomocniczy2 wykorzystamy przy usuwaniu węzłów innych od pierwszego,

• zmienna rozmiar posłuży do ustalenia rozmiaru listy.

Następnie zliczamy elementy listy za pomocą pętli while przechodzącej po wszystkich węzłach listy, zaczynając od pierwszego. Po dojściu do ostatniego elementu w zmiennej pomocniczy1 zostanie zapisana wartość None i pętla zakończy swoje działanie.

Następnie, jeżeli podany indeks nie jest większy od obliczonego rozmiaru listy, zaczynamy usuwanie węzła. Zadanie to realizuje kod, który umieszczamy na końcu omawianej metody:

    # Usuwanie pierwszego węzła
    pomocniczy1 = self.glowa
    if (indeks == 1):
        self.glowa = self.glowa.nastepny
        return

    # Szukanie węzła do usunięcia (innego niż pierwszy)
    while indeks > 1:
        pomocniczy2 = pomocniczy1
        pomocniczy1 = pomocniczy1.nastepny
        indeks -= 1

    # Zmiana referencji nastepny węzła poprzedzającego usuwany
    pomocniczy2.nastepny = pomocniczy1.nastepny

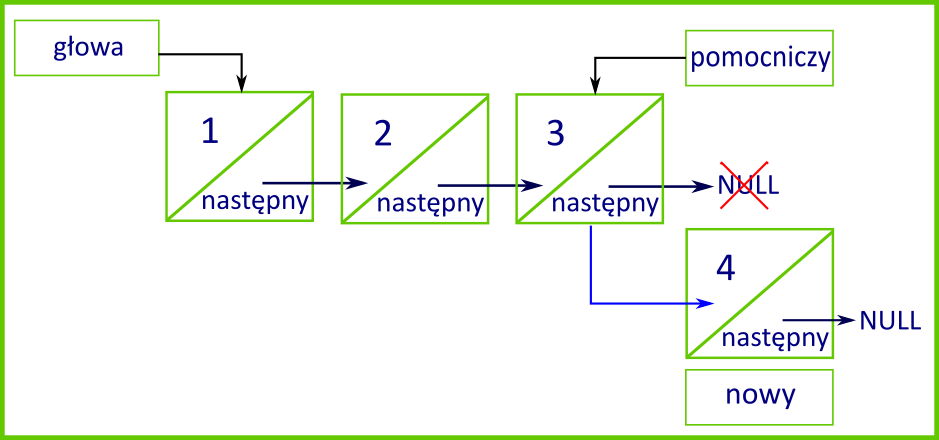
Jeżeli usuwanym elementem jest pierwszy węzeł (indeks 1), pole glowa ustawiamy na następny węzeł, co powoduje wyłączenie dotychczasowego pierwszego elementu z listy.

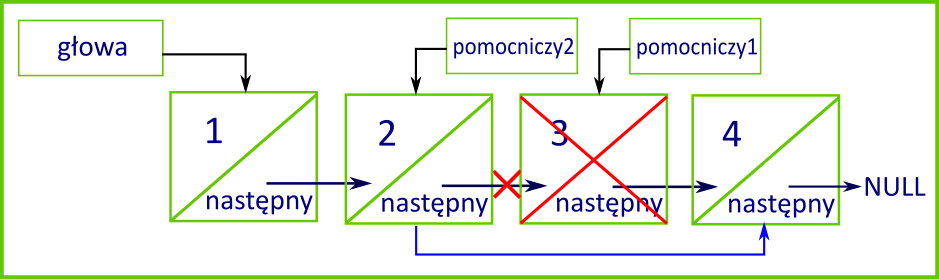
W przeciwnym razie w pętli, która wykonuje się, dopóki indeks jest większy od 1, szukamy węzła do usunięcia. W każdej iteracji indeks jest zmniejszany o 1 dzięki notacji postfiksowej. Wewnątrz pętli przechodzimy po indeks - 1 elementach listy od jej początku, więc po jej zakończeniu zmienna pomocniczy1 będzie wskazywała węzeł do usunięcia, a zmienna pomocniczy2 węzeł poprzedni.

Po zakończeniu pętli w węźle poprzedzającym węzeł usuwany ustawiamy referencję nastepny na węzeł następny po węźle usuwanym (w przypadku usuwania ostatniego węzła będzie to wartość None).

R1DT71fUbiSfA

Ilustracja przedstawia schemat usuwania węzła z listy jednokierunkowej. Lista składa się z czterech elementów, gdzie element pierwszy jest głową, drugi jest elementem pomocniczym dwa a trzeci jest elementem pomocniczym jeden. Element trzeci został przekreślony, wraz ze strzałką pomiędzy elementami pomocniczymi. Z  elementu drugiego prowadzi nowa strzałka prosto do elementu czwartego.

import sys

class Wezel:
    def __init__(self, liczba):
        self.liczba = liczba
        self.nastepny = None

class Lista:
    def __init__(self):
        self.glowa = None

    def czy_pusta(self):
        if self.glowa is None:
            print("Lista jest pusta!")
            return True
        return False

    def dodaj(self, liczba):
        print("Dodaje:", liczba)
        nowy = Wezel(liczba)

        if self.czy_pusta():
            self.glowa = nowy
            return

        pomocniczy = self.glowa
        while pomocniczy.nastepny != None:
            pomocniczy = pomocniczy.nastepny

        pomocniczy.nastepny = nowy

    def usun(self, indeks):
        if self.czy_pusta():
            return

        print("Usuwam pozycje:", indeks)

        pomocniczy1, pomocniczy2 = self.glowa, None
        rozmiar = 0

        while pomocniczy1 != None:
            pomocniczy1 = pomocniczy1.nastepny
            rozmiar += 1

        if indeks > rozmiar:
            print("Indeks poza zakresem.")
            return

        pomocniczy1 = self.glowa
        if (indeks == 1):
            self.glowa = self.glowa.nastepny
            return

        while indeks > 1:
            pomocniczy2 = pomocniczy1
            pomocniczy1 = pomocniczy1.nastepny
            indeks -= 1

        pomocniczy2.nastepny = pomocniczy1.nastepny

    def wypisz(self):
        if self.czy_pusta():
            return

        print("Lista zawiera: ", end="")
        pomocniczy = self.glowa
        while pomocniczy:
            print(pomocniczy.liczba, "", end="")
            pomocniczy = pomocniczy.nastepny;
        print()


lista = Lista()
lista.dodaj(1)
lista.dodaj(2)
lista.dodaj(3)
lista.wypisz()

lista.usun(2)
lista.wypisz()

lista.usun(2)
lista.dodaj(4)
lista.wypisz()

Dodaje: 1
Lista jest pusta!
Dodaje: 2
Dodaje: 3
Lista zawiera: 1 2 3 
Usuwam pozycje: 2
Lista zawiera: 1 3 
Usuwam pozycje: 2
Dodaje: 4
Lista zawiera: 1 4

Lista dwukierunkowa

Lista dwukierunkowa od jednokierunkowej różni się tym, że jej węzły, oprócz referencji na element następny, zawierają także referencję na element poprzedni. Implementację przygotujemy w oparciu o omówiony kod listy jednokierunkowej.

Na początku uzupełniamy klasę Wezel o pole poprzedni i uzupełniamy konstruktor tak, aby inicjalizował je wartością pustą. Do klasy Lista dodajemy pole ogon, które będzie wskazywało ostatni element listy. W konstruktorze klasy pola glowa i ogon ustawiamy na wartości puste.

class Wezel:
    def __init__(self, liczba):
        self.liczba = liczba
        self.nastepny = None
        self.poprzedni = None

class Lista:
    def __init__(self):
        self.glowa = self.ogon = None

    # Poniżej dodamy kolejne metody

Dodawanie węzłów na końcu listy dwukierunkowej

Metody czy_pusta() oraz wypisz() pozostają bez zmian. Modyfikacji wymagają tylko implementacje metod dodaj() i usun(). Zacznijmy od metody dodającej nowe węzły:

def dodaj(self, liczba):
    print("Dodaję:", liczba)

    nowy = Wezel(liczba)

    if self.czy_pusta():
        self.glowa = self.ogon = nowy
        return

    self.ogon.nastepny = nowy
    nowy.poprzedni = self.ogon
    self.ogon = nowy

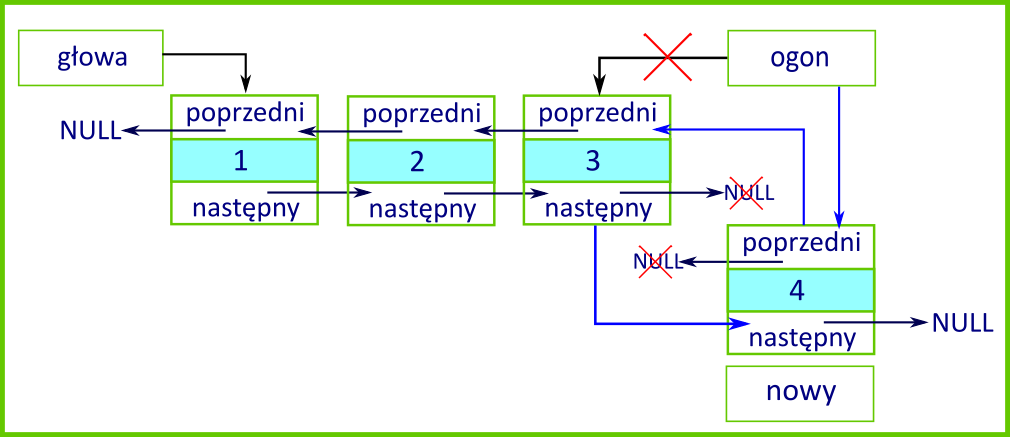
Różnice w porównaniu do implementacji tej metody w przypadku listy jednokierunkowej są następujące:

• ustawienia pola ogon na nowy węzeł w przypadku dodawania pierwszego elementu listy,

• wykorzystanie pola ogon – zamiast pętli przechodzącej wszystkie elementy listy – do wskazania ostatniego węzła listy,

• ustawienie referencji nastepny dotychczasowego ostatniego węzła na nowy oraz poprzedni nowego węzła na dotychczasowy ostatni,

• ustawienie pola ogon na nowo dodany element.

RlhFi1x6RJLwH

Ilustracja przedstawia schemat dodawania węzła do końca listy dwukierunkowej. Lista składa się z czterech elementów. Pomiędzy elementami są po dwie strzałki, gdyż każdy z nich jest jednocześnie elementem następnym oraz poprzednim. Pierwszy z elementów to głowa. Trzeci element początkowo był ogonem, jednak po dodaniu węzła to nowy element czwarty jest podpisany jako ogon.

Usuwanie węzłów z listy dwukierunkowej

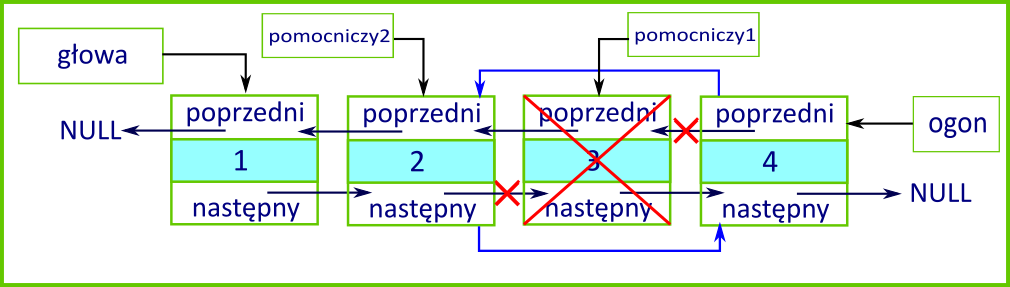
Metoda usuwająca elementy z podanej pozycji nie wymaga zmian, lecz uzupełnienia. Jeżeli usuwamy element niebędący ani pierwszym, ani ostatnim, musimy odpowiednio ustawić referencję poprzedni węzła występującego po węźle usuwanym. W przeciwnym razie, jeżeli usuwamy ostatni element, musimy zaktualizować pole ogon, aby wskazywało na dotychczasowy węzeł przedostatni. Poniżej kod uzupełnionej metody usun(). W komentarzu zaznaczyliśmy instrukcję warunkową realizującą omówione operacje:

def usun(self, indeks):
    if self.czy_pusta():
        return

    print("Usuwam pozycje:", indeks)

    pomocniczy1, pomocniczy2 = self.glowa, None
    rozmiar = 0

    while pomocniczy1 != None:
        pomocniczy1 = pomocniczy1.nastepny
        rozmiar += 1

    if indeks > rozmiar:
        print("Indeks poza zakresem.")
        return

    if (indeks == 1):
        self.glowa = self.glowa.nastepny
        return

    pomocniczy1 = self.glowa
    while indeks > 1:
        pomocniczy2 = pomocniczy1
        pomocniczy1 = pomocniczy1.nastepny
        indeks -= 1

    pomocniczy2.nastepny = pomocniczy1.nastepny

    # Kod obsługujący listę dwukierunkową
    if pomocniczy1.nastepny != None:
        # Jeżeli usuwany węzeł nie jest ostatni
        pomocniczy1.nastepny.poprzedni = pomocniczy2
    else:
        # Jeżeli usuwany element jest ostatni
        self.ogon = pomocniczy2

R50oTO05RitRz

Ilustracja przedstawia schemat usuwania węzła z listy dwukierunkowej. Lista składa się z czterech elementów. Pomiędzy elementami są po dwie strzałki, gdyż każdy z nich jest jednocześnie elementem następnym oraz poprzednim. Pierwszy z elementów to głowa. Element drugi to element pomocniczy dwa. Element trzeci to element pomocniczy jeden. Element czwarty to ogon. Element trzeci został przekreślony wraz ze strzałkami łączącymi go z drugim oraz czwartym elementem. Pomiędzy drugim i czwartym elementem dodane zostały nowe strzałki.

import sys

class Wezel:
    def __init__(self, liczba):
        self.liczba = liczba
        self.nastepny = None
        self.poprzedni = None

class Lista:
    def __init__(self):
        self.glowa = self.ogon = None

    def czy_pusta(self):
        if self.glowa is None:
            print("Lista jest pusta!")
            return True
        return False

    def dodaj(self, liczba):
        print("Dodaje:", liczba)

        nowy = Wezel(liczba)

        if self.czy_pusta():
            self.glowa = self.ogon = nowy
            return

        self.ogon.nastepny = nowy
        nowy.poprzedni = self.ogon
        self.ogon = nowy

    def usun(self, indeks):
        if self.czy_pusta():
            return

        print("Usuwam pozycje:", indeks)

        pomocniczy1, pomocniczy2 = self.glowa, None
        rozmiar = 0

        while pomocniczy1 != None:
            pomocniczy1 = pomocniczy1.nastepny
            rozmiar += 1

        if indeks > rozmiar:
            print("Indeks poza zakresem.")
            return

        if (indeks == 1):
            self.glowa = self.glowa.nastepny
            return

        pomocniczy1 = self.glowa
        while indeks > 1:
            pomocniczy2 = pomocniczy1
            pomocniczy1 = pomocniczy1.nastepny
            indeks -= 1

        pomocniczy2.nastepny = pomocniczy1.nastepny

        if pomocniczy1.nastepny != None:
            pomocniczy1.nastepny.poprzedni = pomocniczy2
        else:
            self.ogon = pomocniczy2

    def wypisz(self):
        if self.czy_pusta():
            return

        print("Lista zawiera: ", end="")
        pomocniczy = self.glowa
        while pomocniczy:
            print(pomocniczy.liczba, "", end="")
            pomocniczy = pomocniczy.nastepny;
        print()


lista = Lista()
lista.dodaj(1)
lista.dodaj(2)
lista.dodaj(3)
lista.wypisz()

lista.usun(1)
lista.usun(3)
lista.usun(2)
lista.dodaj(4)
lista.wypisz()

Dodaje: 1
Lista jest pusta!
Dodaje: 2
Dodaje: 3
Lista zawiera: 1 2 3 
Usuwam pozycje: 1
Usuwam pozycje: 3
Indeks poza zakresem.
Usuwam pozycje: 2
Dodaje: 4
Lista zawiera: 2 4

Klasa deque z modułu collections

Klasa deque udostępnia m. in. następujące metody:

• append() – zadaniem metody jest dodawanie elementu na końcu listy;

• pop() – metoda zwraca ostatni element listy i go usuwa;

• appendleft() – zadaniem metody jest dodawanie elementu na początku listy;

• popleft() – metoda zwraca pierwszy element listy i go usuwa.

Pozostałe funkcjonalności danej struktury (oznaczonej poniżej nazwą s) uzyskujemy za pomocą standardowych mechanizmów języka. Możemy używać następujących instrukcji:

• len(s) – instrukcja zwraca liczbę elementów listy;

• s[0] – zadaniem instrukcji jest zwrócenie bez usuwania pierwszego elementu listy;

• s[-1] lub s[len(s) - 1] – zadaniem instrukcji jest zwrócenie bez usuwania ostatniego elementu listy;

• if s:, while s:, return s – instrukcja sprawdza, czy lista jest pusta; jeśli tak, s przyjmie wartość False, w przeciwnym razie True.

Kontener deque jako stos

from collections import deque

stos = deque()

print("Odkladam liczby 5, 4, 6")
stos.append(5);
stos.append(4);
stos.append(6);
print("Rozmiar:", len(stos), end="")
print(" Wierzcholek:", stos[-1])

print("Zdejmuje wierzcholek:", stos.pop())
print("Rozmiar:", len(stos), end="")
print(" Wierzcholek:", stos[-1])

print("Stos zawiera: ", end="")
while stos:
    print(stos.pop(), "", end="")

print()
print("Rozmiar:", len(stos))

Odkladam liczby 5, 4, 6
Rozmiar: 3 Wierzcholek: 6
Zdejmuje wierzcholek: 6
Rozmiar: 2 Wierzcholek: 4
Stos zawiera: 4 5 
Rozmiar: 0

Kontener deque jako kolejka

from collections import deque

kolejka = deque()

print("Dodaje liczby 5, 4, 6")
kolejka.append(5);
kolejka.append(4);
kolejka.append(6);
print("Rozmiar:", len(kolejka), end="")
print(" Pierwszy:", kolejka[0], end="")
print(" Ostatni:", kolejka[-1])

print("Usuwam pierwszy: ", kolejka.popleft())
print("Rozmiar:", len(kolejka), end="")
print(" Pierwszy:", kolejka[0], end="")
print(" Ostatni:", kolejka[-1])

print("Lista zawiera: ", end="")
while kolejka:
    print(kolejka.popleft(), "", end="")

print()
print("Rozmiar:", len(kolejka))

Dodaje liczby 5, 4, 6
Rozmiar: 3 Pierwszy: 5 Ostatni: 6
Usuwam pierwszy:  5
Rozmiar: 2 Pierwszy: 4 Ostatni: 6
Lista zawiera: 4 6 
Rozmiar: 0

Kontener deque jako lista

from collections import deque

lista = deque()

print("Dodaje liczby 5, 4 na koncu")
lista.append(5);
lista.append(4);
print("Dodaje liczbe 6 na poczatku")
lista.appendleft(6)
print("Rozmiar:", len(lista), end="")
print(" Pierwszy:", lista[0], end="")
print(" Ostatni:", lista[-1])

print("Usuwam ostatni: ", lista.pop())
print("Rozmiar:", len(lista), end="")
print(" Pierwszy:", lista[0], end="")
print(" Ostatni:", lista[-1])

print("Lista zawiera: ", end="")
while lista:
    print(lista.popleft(), "", end="")

print()
print("Rozmiar:", len(lista))

Dodaje liczby 5, 4 na koncu
Dodaje liczbe 6 na poczatku
Rozmiar: 3 Pierwszy: 6 Ostatni: 4
Usuwam ostatni:  4
Rozmiar: 2 Pierwszy: 6 Ostatni: 5
Lista zawiera: 6 5 
Rozmiar: 0

Słownik