Przeczytaj

Rozpoczniemy od klasycznego problemu optymalizacji.

Przykład 1

Odpowiemy na pytanie, który prostokąt wśród wszystkich o obwodzie $4$ ma największe pole?

Rozwiązanie

Oznaczmy przez $x$ długość jednego z boków. Ponieważ obwód rozważanego prostokąta wynosi $4$ , długość boku $x$ musi być mniejsza niż $2$ . Ze wzoru na obwód prostokąta otrzymujemy, że jeżeli $y$ jest długością drugiego boku, to

$2 x + 2 y = 4$

$2 y = 4 - 2 x$

$y = 2 - x$ .

Pole prostokąta wyraża się wzorem $x y = x (2 - x)$ . Reasumując, jeżeli jeden z boków wynosi $x \in (0, 2)$ , to jego pole jest równe $x (2 - x)$ . Sprowadziliśmy zatem wyjściowy problem do znalezienia największej wartości funkcji $f (x) = x (2 - x)$ na przedziale $(0, 2)$ . Funkcja $f$ jest funkcją kwadratową o ramionach skierowanych do dołu. Jej wartość największa jest więc przyjmowana w wierzchołku. Funkcja $f$ jest w postaci iloczynowej. Odczytujemy więc natychmiast, że miejsca zerowe $f$ wynoszą kolejno

$x_{1} = 0$ , $x_{2} = 2$ .

Pierwsza współrzędna wierzchołka jest równo odległa od obu miejsc zerowych i musi wynosić $1$ . Otrzymujemy więc, że spośród wszystkich prostokątów o obwodzie $4$ największe pole ma ten o bokach $1$ , $1$ , $1$ , $1$ , a więc kwadrat.

Przykładem bardziej skomplikowanych zastosowań może być następujący problem.

Przykład 2

Zginamy arkusz blachy o wymiarach $10 \times 16$ równolegle do krótszej krawędzi w rurę o prostokątnym przekroju. Jak powinniśmy to zrobić, jeżeli chcemy, by otrzymana rura posiadała jak największe pole przekroju?

Rozwiązanie

Oczywiście jedno ze zgięć będzie przebiegało dokładnie po środku arkusza.

R1ZZiYtAfBTJX

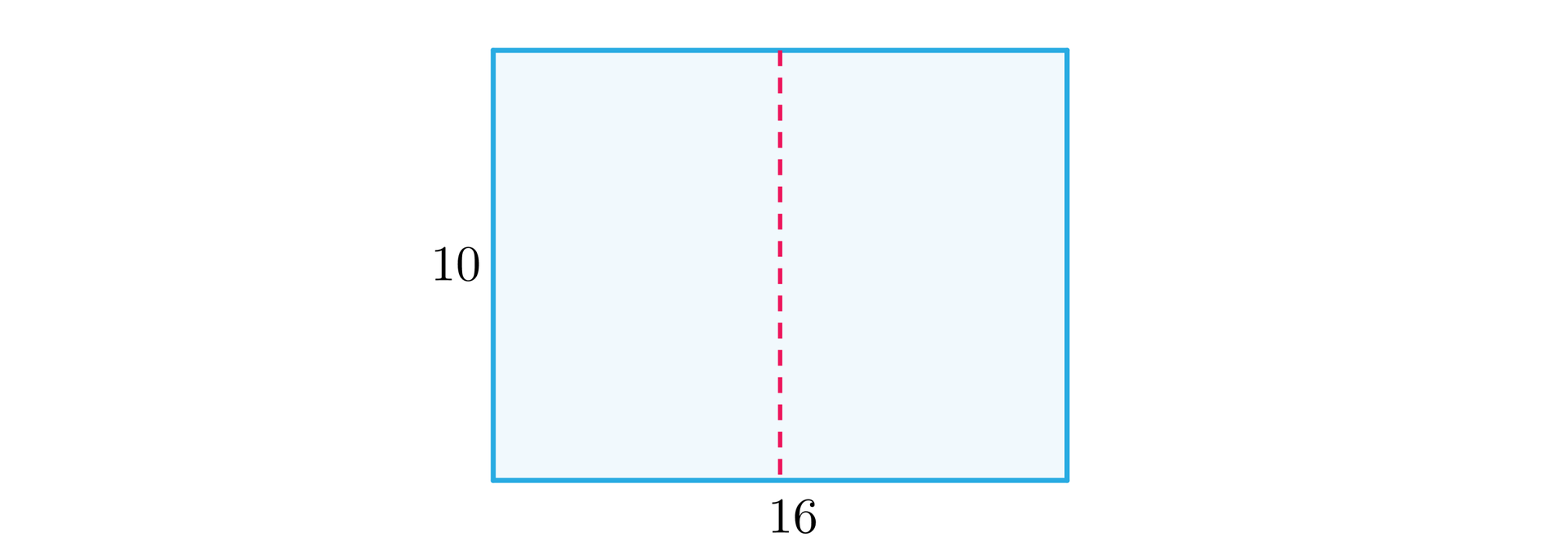
Ilustracja przedstawia prostokąt o bokach 10 i szesnaście. Przez połowę dłuższego boku przebiega przerywana linia.

Kolejne dwa będą równo odległe od, kolejno, środkowego zgięcia oraz boku.

RlOtP5vmXhisg

Ilustracja przedstawia prostokąt o bokach 10 i szesnaście. Przez połowę dłuższego boku przebiega przerywana linia. Dłuższy bok podzielono na cztery części. Dwie o długości 8 minus x oraz dwie o długości x. Zbudowano prostopadłościan o wymiarach 8 minus x, 10, x.

Przekrój jest zatem prostokątem o bokach $x$ oraz $8 - x$ . Pole tego przekroju wynosi zatem $x (8 - x)$ . Co za tym idzie wyjściowy problem został, podobnie jak poprzednio, sprowadzony do znalezienia największej wartości funkcji $f (x) = x (8 - x)$ na przedziale $(0, 8)$ . Tym razem posłużymy się jednak wykresem funkcji $f$ .

RF5c05mCPmY1X

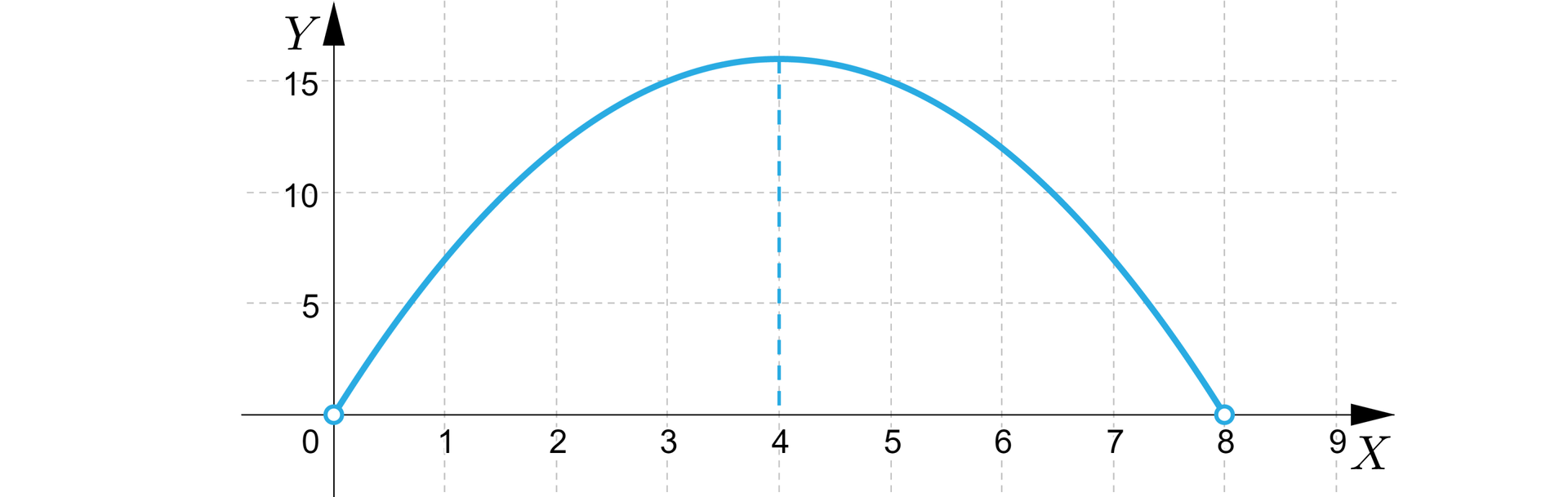
Ilustracja przedstawia układ współrzędnych o osi pionowej od 0 do 15 oraz osi poziomej od zera do dziewięciu. Zaznaczono fragment paraboli z ramionami skierowanymi w dół od miejsca zerowego równego 0 do drugiego miejsca zerowego osiem. Obydwa zaznaczone są niezamalowanym kółeczkiem.

Łatwo zauważyć, że największa wartość jest przyjmowana w punkcie $4$ . Pole przekroju wynosi zatem $4 \cdot 4 = 16$ .

Można się zastanowić jaki przekrój będzie miała otrzymana rura jeżeli rozważany arkusz blachy zegniemy w rurę o przekroju okrągłym.

R14J4mnO0WgS4

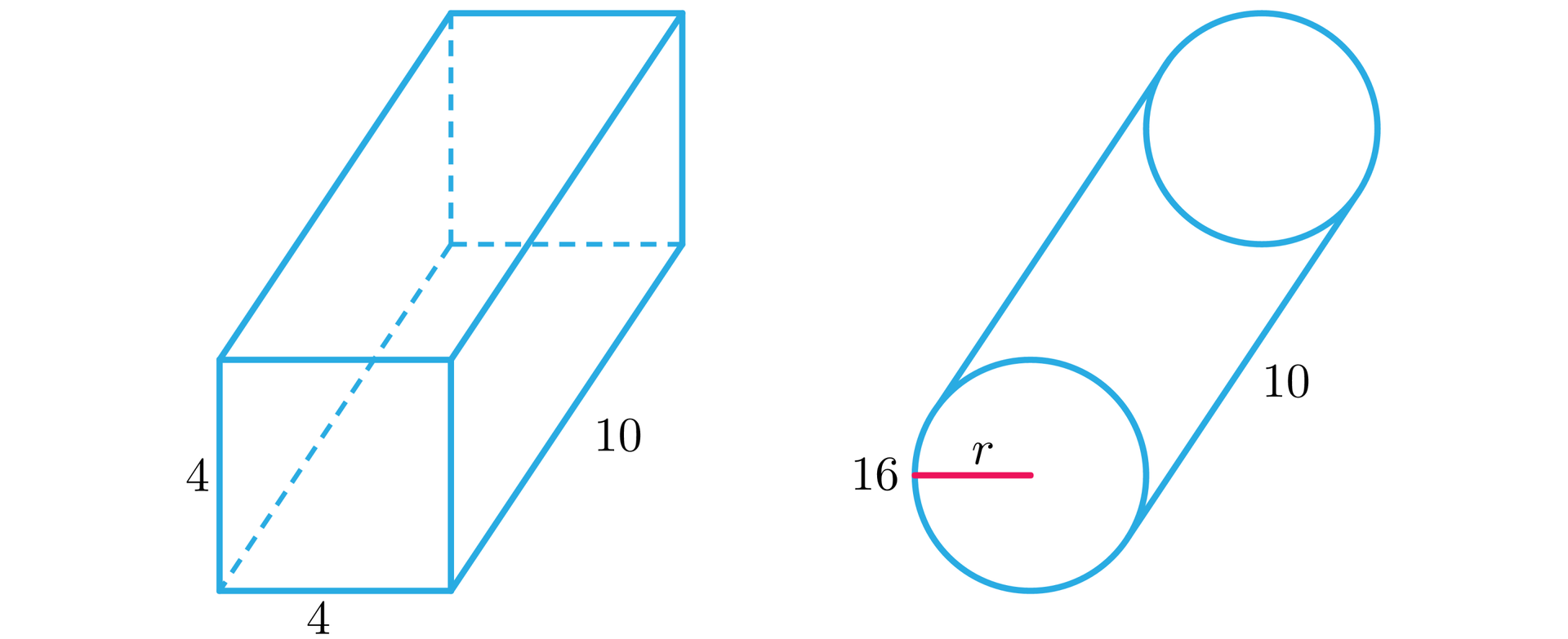
Ilustracja przedstawia prostopadłościan o wymiarach szerokość 4, długość 10 oraz wysokość 4. Oraz walec o długości 10 i obwodzie okręgu równym szesnaście.

Oznaczmy promień tego przekroju przez $r$ . Obwód okręgu wynosi $16$ , a więc otrzymujemy równanie:

$2 π r = 16$

$r = \frac{8}{π}$ .

Przekrój wynosi zatem:

$π r^{2} = π {(\frac{8}{π})}^{2} = \frac{64}{π}$ .

Wykorzystamy teraz niewymagającą dodatkowego komentarza nierówność: $π < 4$ . Otrzymujemy:

$16 = \frac{16 π}{π} < \frac{16 \cdot 4}{π} = \frac{64}{π}$

Ostatecznie okazuje się, że rura o przekroju okrągłym ma większy przekrój niż rura o przekroju prostokątnym, o ile założymy, że obie rury były wykonane z identycznych arkuszy blachy.

Należy podkreślić, że nie każdy problem optymalizacyjny posiada rozwiązanie.

Przekonamy się o tym, nieznacznie modyfikując rozważany już przykład.

Przykład 3

Czterometrowy drut zginamy w taki sposób, by otrzymać prostokątną ramkę. Jak powinniśmy to zrobić, by pole otrzymanego prostokąta było najmniejsze? Czy jest to możliwe?

Rozwiązanie

Funkcja $f$ przyporządkowuje bokowi $x$ pole prostokąta o wymiarach $x \times (2 - x)$ . W przykładzie $1$ poszukiwaliśmy największej wartości funkcji $f (x) = x (2 - x)$ na przedziale $(0, 4)$ , aby znaleźć największe możliwe pole. Obecnie, aby znaleźć proporcję boków dającą najmniejsze pole musielibyśmy znaleźć najmniejszą wartość funkcji $f$ na przedziale $(0, 4)$ . Rysując wykres funkcji $f$ przekonujemy się, że minimum na przedziale $(0, 4)$ nie jest osiągane, gdyż najmniejsza wartość musiałaby wynosić $0$ . Nie jest jednak możliwe, by pole prostokąta było równe $0$ . Sformułowany powyżej problem polegający na znalezieniu najmniejszego pola nie posiada zatem rozwiązania.

Nieocenioną pomocą w weryfikowaniu tego czy dany problem ma rozwiązanie okazuje się być twierdzenie Weierstrassa, które przytoczymy poniżej

Weierstrassa

Twierdzenie: Weierstrassa

Jeżeli funkcja $f : ⟨a, b⟩ ⟶ ℝ$ jest ciągła, to istnieją takie punkty $c$ , $d \in ⟨a, b⟩$ , że dla każdego $x \in ⟨a, b⟩$ zachodzi

f (c) \leq f (x) \leq f (d)

Przykład 4

Dom pana $X$ znajduje się na mapie w początku układu współrzędnych. Szlak widokowy znajdujący się w pobliżu domu pana $X$ układa się w krzywą będącą wykresem funkcji $f (x) = 1 - x^{2}$ dla $x \in ⟨- 1, 1⟩$ . Wyznaczymy miejsca na szlaku, które znajdują się najbliżej domu pana $X$ oraz te, które znajdują się najdalej.

Rozwiązanie

RyRDcPEPVfxKs

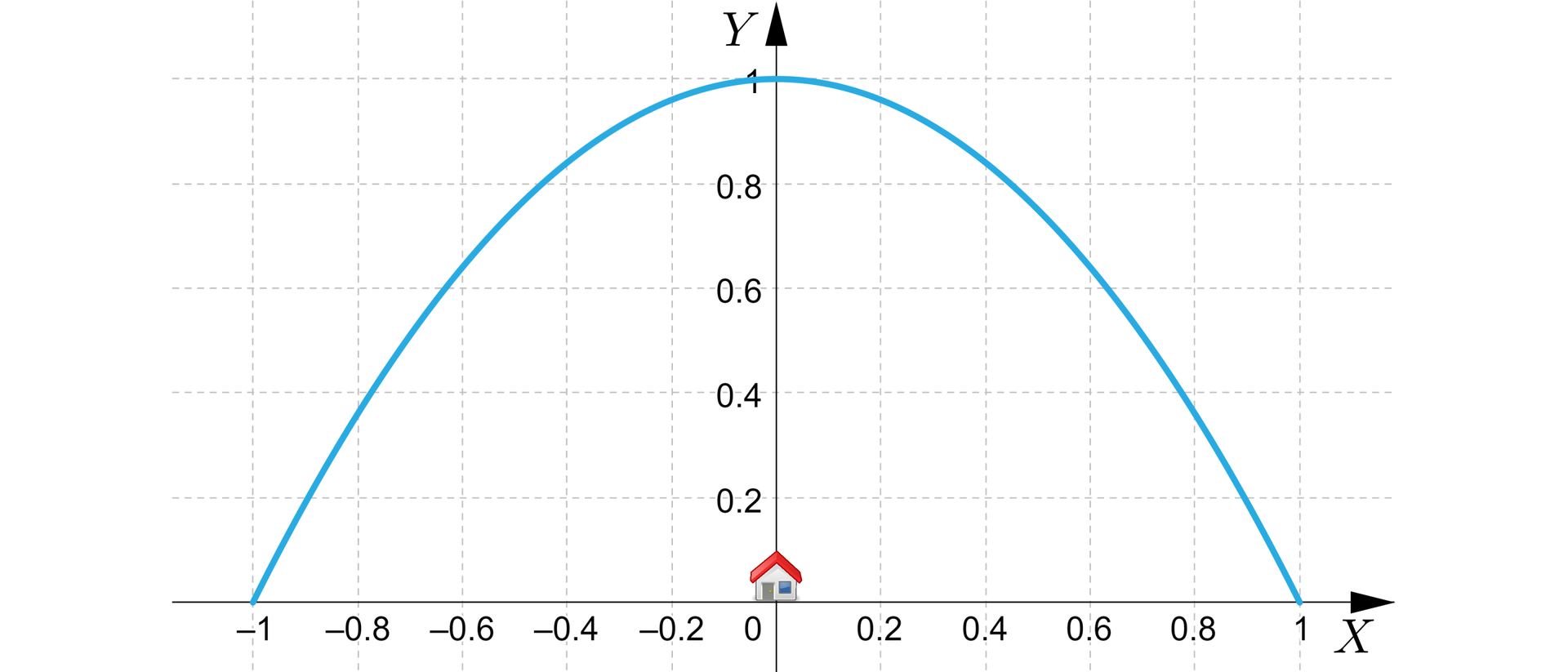
Ilustracja przedstawia układ współrzędnych z poziomą osią od minus jeden do jeden oraz pionową od zera do jednego. Dom znajduję się w początku układu współrzędnych. Zaznaczono fragment paraboli z ramionami skierowanymi w dół od miejsca zerowego równego minus jeden do miejsca zerowego równego jeden.

Wybierzmy dowolny punkt znajdujący się na szlaku. Skoro należy on do wykresu musi być postaci:

$(x, f (x)) = (x, 1 - x^{2})$ , dla pewnego $x \in ⟨- 1, 1⟩$ .

Odległość tak wybranego punktu od początku układu współrzędnych obliczmy korzystając ze wzoru na odległość między dwoma punktami.

$|(0, 0), (x, 1 - x^{2})| = \sqrt{{(x - 0)}^{2} + {(0 - 1 + x^{2})}^{2}} = \sqrt{x^{2} + 1 - 2 x^{2} + x^{4}} =$

$= \sqrt{1 - x^{2} + x^{4}}$

Każdy punkt $x \in ⟨- 1, 1⟩$ wyznacza zatem dokładnie jeden punkt na ścieżce, którego odległość od początku układu współrzędnych wynosi $\sqrt{1 - x^{2} + x^{4}}$ . Aby dokończyć zadanie musimy zatem znaleźć ekstrema funkcjiekstremum funkcjiekstrema funkcji $g : ⟨- 1, 1⟩ ⟶ ℝ$ określonej wzorem:

$g (x) = \sqrt{1 - x^{2} + x^{4}}$ .

Pierwiastek z danego wyrażenia będzie tym większy im większa będzie wartość tego wyrażenia. Analogicznie, im mniejsza będzie wielkość, tym mniejszy będzie jej pierwiastek. Wystarczy zatem, że poszukamy najmniejszej i największej wartości wyrażenia:

$1 - x^{2} + x^{4}$ .

Na przedziale $⟨- 1, 1⟩$ twierdzenie Weierstrassa zapewnia nam, że ten problem posiada rozwiązanie. Wyznaczmy zatem ekstrema funkcji $h (x) = 1 - x^{2} + x^{4}$ , która jest różniczkowalna na przedzialefunkcja różniczkowalna w zbiorze $A$ różniczkowalna na przedziale $(- 1, 1)$ . Jeżeli więc przyjmuje najmniejszą lub największą wartość w $(- 1, 1)$ , to musi mieć tam zerową pochodną, tj. musi zachodzić:

$h^{'} (x) = - 2 x + 4 x^{3} = 2 x (x^{2} - 2) = 0$ .

Łatwo zauważyć, że powyższe równanie posiada dokładnie trzy rozwiązania: $- \frac{\sqrt{2}}{2}$ , $0$ , $\frac{\sqrt{2}}{2}$ . Zauważmy, że nasze rozważania pomijały punkty znajdujące się na końcach przedziału. Uwzględnimy je teraz. Ostatecznie więc jedyne punkty, w których funkcja $h$ może przyjmować wartości największe lub najmniejsze to $- 1$ , $- \frac{\sqrt{2}}{2}$ , $0$ , $\frac{\sqrt{2}}{2}$ , $1$ . Policzmy wartości w tych punktach:

$h (- 1) = 1$

$h (- \frac{\sqrt{2}}{2}) = \frac{3}{4}$

$h (0) = 1$

$h (\frac{\sqrt{2}}{2}) = \frac{3}{4}$

$h (1) = 1$

Otrzymujemy zatem, że funkcja $h$ , a co za tym idzie także funkcja $g$ , przyjmuje największe wartości w punktach $- 1$ , $0$ oraz $1$ , zaś najmniejsze wartości przyjmowane są w punktach $- \frac{\sqrt{2}}{2}$ i $\frac{\sqrt{2}}{2}$ . Wracając do wyjściowych interpretacji omawianych wielkości mamy, iż miejsca na ścieżce widokowej, które znajdują się najdalej domu pana $X$ mają współrzędne $(- 1, 0)$ , $(0, 1)$ oraz $(1, 0)$ . Z kolei te znajdujące się najbliżej to $(- \frac{\sqrt{2}}{2}, \frac{1}{2})$ i $(\frac{\sqrt{2}}{2}, \frac{1}{2})$ .

Przykład 5

Mamy do dyspozycji prostokątny arkusz tektury o wymiarach $4 \times 6$ . Chcemy wykonać z niego prostopadłościenne pudełko. W tym celu wycinamy identyczny kwadrat w każdym z rogów, a następnie składamy otrzymane boki zgodnie z zamieszczoną poniżej grafiką.

RbDPLqVjGUamS

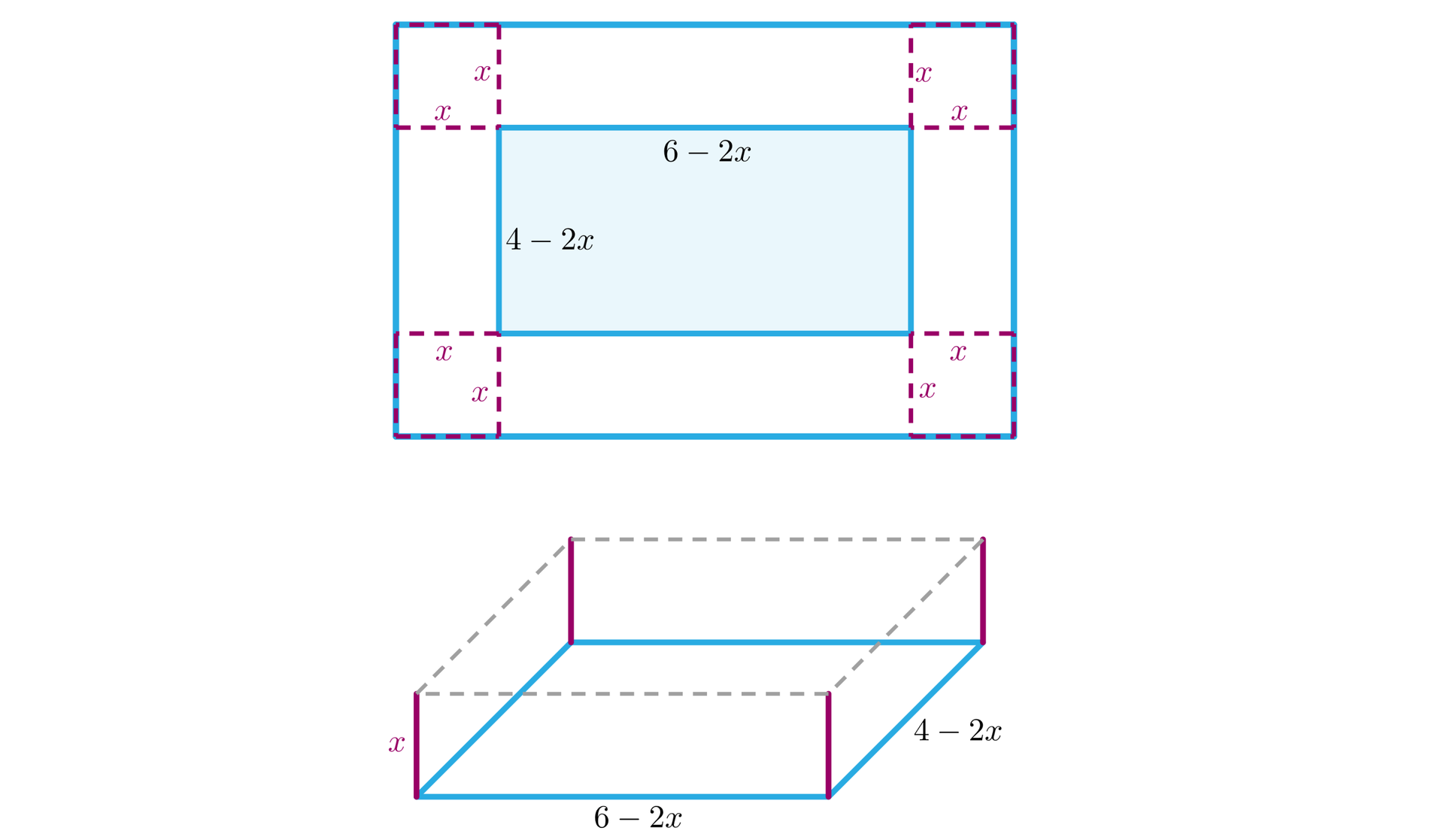
Ilustracja przedstawia prostokąt o wymiarach 6 i cztery. W każdym z rogów zaznaczono kwadrat o boku x. W środku prostokąta utworzono mniejszy o wymiarach 6 minus 2 x oraz 4 minus dwa x. Z prostokąta utworzono prostopadłościan o wymiarach szerokość 6 minus 2x, długość 4 minus dwa x oraz wysokość x.

Znajdziemy takie wymiary wycinanych przez nas kwadratów, dla których otrzymane pudełko ma możliwie największą objętość.

Rozwiązanie

Oznaczmy przez $x$ długość boku, który będzie wycinany. Wymiary otrzymanego pudełka to wówczas $x \times (4 - 2 x) \times (6 - 2 x)$ . Jest jasne, że musi zachodzić:

$x > 0$ ,

$4 - 2 x > 0$ ,

$6 - 2 x > 0$ .

Przekształcając powyższe równania otrzymujemy:

$x > 0$ ,

$x < 2$ ,

$x < 3$ .

Ostatecznie $x \in (0, 2)$ . Objętość otrzymanego pudełka wynosi więc $x (4 - 2 x) (6 - 2 x) = 4 x (2 - x) (3 - x)$ . Znalezienie rozwiązania będzie zatem wymagało znalezienia maksimum funkcji

$f (x) = 4 x (2 - x) (3 - x) = 4 x^{3} - 20 x^{2} + 24 x$ , na przedziale $(0, 2)$ .

Funkcja $f$ jest wprawdzie ciągła, ale zbiór, na którym ją rozważamy nie jest przedziałem domkniętym. Nic jednak nie stoi na przeszkodzie, by znaleźć największą wartość funkcji $f$ na przedziale $⟨0, 2⟩$ . Twierdzenie Weierstrassa zapewnia nam rozwiązywalność tak postawionego problemu. Dokładne wyznaczenie punktu, w którym funkcja $f$ przyjmuje wartość największą będzie już jednak trudniejsze. Funkcja $f$ jest różniczkowalna, więc wartości ekstremalne może przyjmować jedynie na końcach przedziału $⟨0, 2⟩$ lub w tych punktach, w których zeruje się pochodna $f$ . Policzmy zatem

$f^{'} (x) = 4 \cdot 3 x^{2} - 20 \cdot 2 x + 24 = 12 x^{2} - 40 x + 24$ .

Rozwiązujemy równanie kwadratowe:

$12 x^{2} - 40 x + 24 = 0 | : 4$

$3 x^{2} - 10 x + 6 = 0$

$∆ = {(- 10)}^{2} - 4 \cdot 3 \cdot 6 = 100 - 72 = 28$

$x_{1} = \frac{10 - 2 \sqrt{7}}{6} = \frac{5 - \sqrt{7}}{3} \in (0, 2)$

$x_{2} = \frac{10 + 2 \sqrt{7}}{6} = \frac{5 + \sqrt{7}}{3} \notin (0, 2)$

Otrzymujemy zatem, że funkcja $f$ posiada co najwyżej jedno ekstremum na przedziale $(0, 2)$ . Wartości na końcach przedziału są sobie równe i wynoszą $f (0) = f (2) = 0$ . Zauważmy, że wartość funkcji $f$ w punkcie $\frac{5 - \sqrt{7}}{3}$ jest dodatnia, gdyż odpowiada ona objętości pewnego prostopadłościennego pudełka. Oznacza to, że funkcja $f$ przyjmuje największą wartość właśnie w punkcie $\frac{5 - \sqrt{7}}{3}$ . Co za tym idzie, aby uzyskać pudełko o możliwie największej objętości powinniśmy wyciąć kwadraty o bokach równych $\frac{5 - \sqrt{7}}{3}$ .

Słownik

ekstremum funkcji

najmniejsza lub największa wartość funkcji

funkcja różniczkowalna w zbiorze

A

funkcja różniczkowalna w zbiorze

A

funkcja, która posiada pochodną w każdym punkcie zbioru $A$

Wprowadzenie

Prezentacja multimedialna

Słownik