Układem równań liniowych z dwiema niewiadomymi nazywamy koniunkcję dwóch równań pierwszego stopnia z dwiema niewiadomymi.

Układ taki przyjmuje postać:

gdzie:
$x$ oraz $y$ – oznaczają niewiadome,
$a_1$, $a_2$, $b_1$ oraz $b_2$ – współczynniki przy niewiadomych $x$ oraz $y$,
$c_1$ i $c_2$ – nazywamy wyrazami wolnymi.

Przy czym współczynniki przy odpowiednich niewiadomych nie są równocześnie zerami.

Znajdziemy dwie liczby naturalne, takie, że ich suma wynosi $10$, a ich różnica $4$.

Zapiszemy warunki podane w treści zadania za pomocą dwóch równań z dwiema niewiadomymi. Pierwszą z liczb oznaczymy $x$, a drugą $y$.

Wtedy $x+y=10$ i $x-y=4$.

Warunki te możemy zapisać w postaci układu równań liniowych z dwiema niewiadomymiukład równań liniowych z dwiema niewiadomymiukładu równań liniowych z dwiema niewiadomymi

$\left\{\begin{array}{l}x+y=10\\ x-y=4 \end{array}\right.$.

Łatwo odgadnąć, że szukane liczby to $x=7$ i $y=3$.

Sprawdzimy, czy spełniają one nasze równania, czyli czy po podstawieniu wartości $x=7$ i $y=3$ do równań w miejsca niewiadomych otrzymamy tożsamości.

Pierwsze równanie.

$L_1=x+y=7+3=10=P_1$

A zatem para $\left(7,3\right)$ spełnia to równanie.

Drugie równanie.

$L_2=x-y=7-3=4=P_2$

A zatem para $\left(7,3\right)$ spełnia to równanie.

Para $\left(7,3\right)$ spełnia każde z równań, a więc spełnia układ tych równań $\left\{\begin{array}{l}x+y=10\\ x-y=4\end{array}\right.$.

Rozwiązaniem układu równań liniowych z dwiema niewiadomymi nazywamy każdą  parę liczb spełniającą jednocześnie każde równanie danego układu równań.

Sprawdzimy, która para liczb $\left(2,3\right)$, $\left(-6,9\right)$ jest rozwiązaniem układu równań

$\left\{\begin{array}{l}\frac{1}{2}x+\frac{2}{3}y=3\\ \frac{1}{7}x+\frac{2}{7}y+\frac{2}{7}=2\end{array}\right.$.

W przypadku takiego układu trudno jest odgadnąć rozwiązanie.

Musimy więc sprawdzić wartości liczbowe wyrażeń  uzyskanych po prawej i lewej stronie każdego z równań układu, po podstawieniu  w miejsce niewiadomych odpowiednich liczb.

Jeśli lewa strona równania będzie równa prawej $\left(L=P\right)$, w każdym z dwóch równań, to para spełnia układ równań, a więc jest jego rozwiązaniem.

Para $\left(2,3\right)$.

Pierwsze równanie.

$L_1=\frac{1}{2}x+\frac{2}{3}y=\frac{1}{2}·2+\frac{2}{3}·3=1+2=3=P_1$

A zatem para $\left(\mathrm{2,} 3\right)$ spełnia to równanie.

Drugie równanie.

$L_2=\frac{1}{7}x+\frac{2}{7}y+\frac{2}{7}=\frac{1}{7}·2+\frac{2}{7}·3+\frac{2}{7}=\frac{2+6+2}{7}=\frac{10}{7}\ne 2=P_2$

A zatem para $\left(2,3\right)$ nie spełnia tego równania.

Nie jest więc rozwiązaniem układu równańrozwiązanie układu równań liniowych z dwiema niewiadomymirozwiązaniem układu równań.

Para $\left(-6,9\right)$.

Pierwsze równanie.

$L_1=\frac{1}{2}x+\frac{2}{3}y=\frac{1}{2}·\left(-6\right)+\frac{2}{3}·9=-3+6=3=P_1$

A zatem para $\left(-6,9\right)$ spełnia to równanie.

Drugie równanie.

$L_2=\frac{1}{7}x+\frac{2}{7}y+\frac{2}{7}=\frac{1}{7}·\left(-6\right)+\frac{2}{7}·9+\frac{2}{7}=\frac{-6+18+2}{7}=\frac{14}{7}=2=P_2$

A zatem para $\left(-6,9\right)$ spełnia to równanie.

Para $\left(-6,9\right)$ spełnia każde z równań, a więc jest rozwiązaniem układu równań $\left\{\begin{array}{l}\frac{1}{2}x+\frac{2}{3}y=3\\ \frac{1}{7}x+\frac{2}{7}y=\frac{2}{7}=2\end{array}\right.$.

Wróćmy teraz do problemu, który pojawił się na początku materiału.

Bartek i Tomek mają razem $780 \mathrm{zł}$ oszczędności. Jednak Tomek ma o $250 \mathrm{zł}$ więcej od Bartka. Jak policzyć ile oszczędności ma każdy z chłopców?  Czy jest tylko jedna prawidłowa odpowiedź na to pytanie?

Oznaczymy przez $x$ oszczedności Bartka, a przez $y$ oszczędności Tomka.

Warunki wynikające z treści zadania możemy zapisać w postaci układu równań liniowych z dwiema niewiadomymi

$\left\{\begin{array}{l}x+y=780\\ y=x+250\end{array}\right.$.

Aby odpowiedzieć, czy jest tylko jedna prawidłowa odpowiedź na to pytanie, możemy narysować wykresy równań i sprawdzić ile mają punktów wspólnych.

RWZkJK9wiXdoV

Grafika przedstawia układ współrzędnych z poziomą osią x od minus czterystu do ośmiuset i pionową osią y od minus dwustu do siedmiuset. Na płaszczyźnie zaznaczone zostały dwie proste, pierwsza o równaniu $y=x+250$ i druga o równaniu $x+y=780$. Proste przecinają się w jednym punkcie.

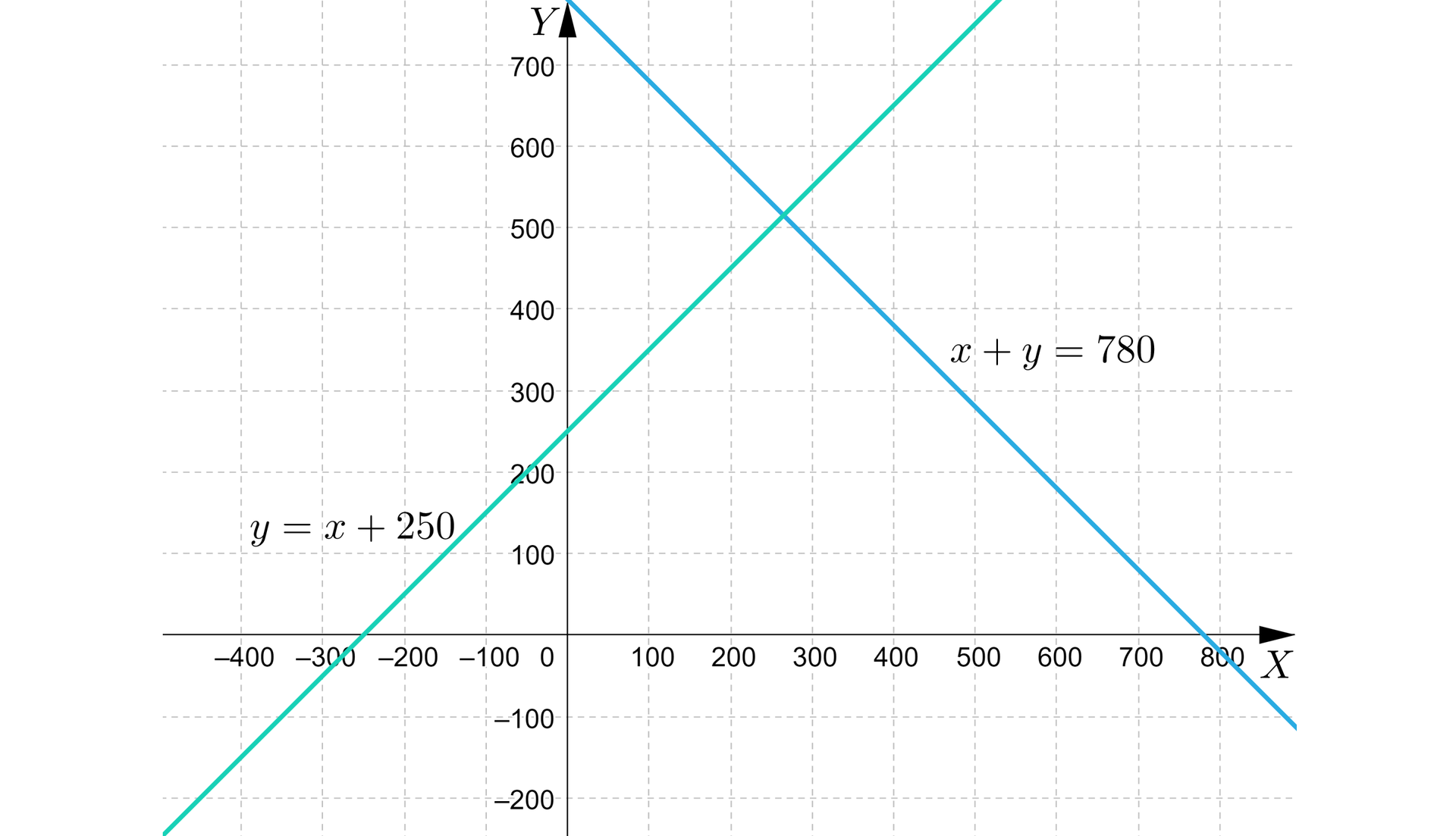
Widzimy, że wykresy mają jeden punkt wspólny, a więc istnieje tylko jedna para liczb, spełniająca jednocześnie obydwa równania, zatem istnieje tylko jedno rozwiązanie tego układu równań.

Aby je znaleźć,  możemy łatwo zapisać układ równań w postaci jednego równania z jedną niewiadomą.

$x+x+250=780$

$2x=780-250$

$x=265$

A wtedy korzystając z drugiego równania obliczmy $y$.

$y=x+250=265+250=515$.

Możemy zatem odpowiedzieć na pytanie:

Bartek ma $265 \mathrm{zł}$ oszczędności, a Tomek ma $515 \mathrm{zł}$.

Istnieje tylko jedna para liczb, będąca rozwiązaniem tego układu równań i spełniająca warunki zadania.

Układ równań liniowych z dwiema niewiadomymi, którego rozwiązaniem jest dokładnie jedna para liczb, nazywamy układem oznaczonym.

Znajdźmy rozwiązania układu równań liniowych

$\left\{\begin{array}{l}\frac{2}{3}y-\frac{1}{3}x=\frac{1}{3}y+1-x\\ 5x+\frac{1}{2}y+\frac{1}{2}=2+4x\end{array}\right.$.

Każde z równań układu przekształcamy równoważnie doprowadzając do najprostszej postaci.

$\left\{\begin{array}{l}\frac{2}{3}y-\frac{1}{3}x=\frac{1}{3}y+1-x \left|·3\right.\\ 5x+\frac{1}{2}y+\frac{1}{2}=2+4x \left|·2\right.\end{array}\right.$

$\left\{\begin{array}{l}2y-x=1y+3-3x\\ 10x+y+1=4+8x\end{array}\right.$

$\left\{\begin{array}{l}2x+y=3\\ 2x+y=3\end{array}\right.$

Otrzymaliśmy takie same równania, a więc ich wykresy pokrywają się.

RcCv784fbLzmb

Grafika przedstawia układ współrzędnych z poziomą osią x od minus 5 do pięciu i pionową osią y od minus trzech do pięciu. Na płaszczyźnie zaznaczona została prosta o równaniu $2x+y=3$

Proste mają zatem nieskończenie wiele punktów wspólnych, a ten układ równań spełnia nieskończenie wiele par liczb.

Pary te są tożsame ze współrzędnymi wszystkich punktów leżących na prostej o równaniu $y=-2x+3$.

A zatem rozwiązaniem układu równań

$\left\{\begin{array}{l}\frac{2}{3}y-\frac{1}{3}x=\frac{1}{3}y+1-x\\ 5x+\frac{1}{2}y+\frac{1}{2}=2+4x\end{array}\right.$.

jest każda para liczb rzeczywistych postaci $\left(x,-2x+3\right)$, gdzie $x\in \mathrm{ℝ}$.

Układ równań liniowych z dwiema niewiadomymi, którego rozwiązaniem jest nieskończenie wiele par liczb, nazywamy układem nieoznaczonym.

Poszukajmy teraz rozwiązań układu równań

$\left\{\begin{array}{l}6x-2y-3=4x-1\\ 0,5x-0,5y+2,5=2\end{array}\right.$.

Każde z równań układu przekształcamy równoważnie doprowadzając do najprostszej postaci.

$\left\{\begin{array}{l}6x-2y-3=4x-1\\ 0,5x-0,5y+2,5=2\end{array}\right.$

$\left\{\begin{array}{l}2x-2y=2 \left|:2\right.\\ 0,5x-0,5y=-0,5 \left|·2\right.\end{array}\right.$

$\left\{\begin{array}{l}x-y=1\\ x-y=-1\end{array}\right.$

$\left\{\begin{array}{l}y=x-1\\ y=x+1\end{array}\right.$

Otrzymaliśmy dwa równania, których wykresy są równoległe i nie mają punktów wspólnych.

R1X59pZAkFpVK

Grafika przedstawia układ współrzędnych z poziomą osią x od minus pięciu do pięciu i pionową osią y od minus czterech do czterech. Na płaszczyźnie zaznaczone zostały dwie proste, pierwsza o równaniu $y=x+1$ i druga o równaniu $y=x-1$. Proste są do siebie równoległe.

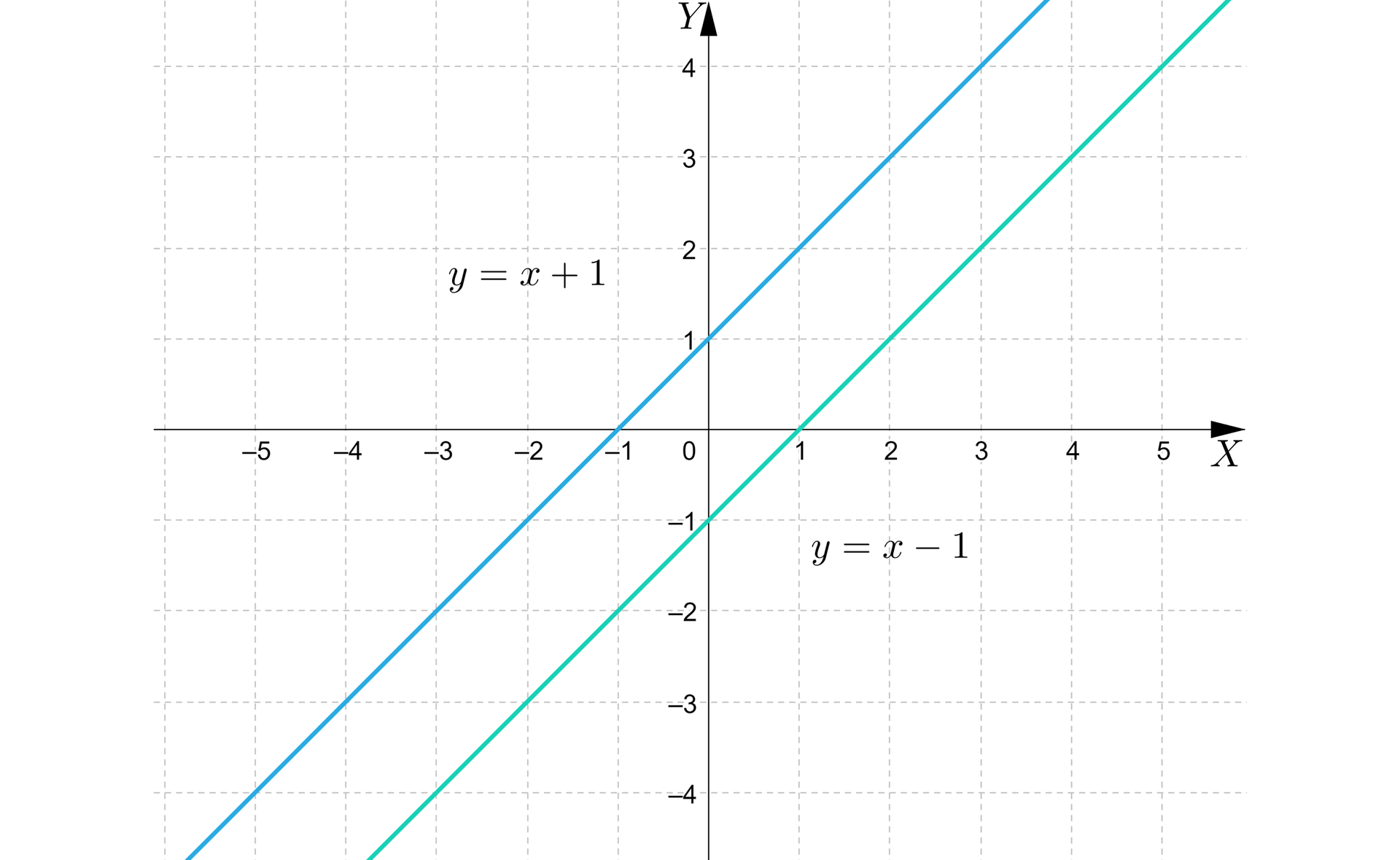
Układ równań nie ma zatem rozwiązania.

Układ równań liniowych z dwiema niewiadomymi, który nie posiada rozwiązań, nazywamy układem sprzecznym.

układ równań liniowych (współczynniki przy odpowiednich zmiennych nie są   równocześnie zerami)  postaci:

para liczb spełniających jednocześnie  każde z równań składowych w tym układzie