Przeczytaj

bg‑turquoise

Iloczyn rozpuszczalności

Pewne związki chemiczne, w których występują wiązania jonowe, są trudno rozpuszczalne w wodzie. Ta niewielka ilość substancji jonowej (soli lub wodorotlenku), która ulegnie rozpuszczeniu, rozpada się całkowicie na jony. W naczyniu ustala się zatem równowaga pomiędzy stałym osadem nierozpuszczonej soli lub wodorotlenku, a jonami znajdującymi się w roztworze.

Równowagę procesu rozpuszczania trudno rozpuszczalnego osadu opisuje równanie:

M_{m} X_{x} ⇄ m M^{x +} + {xX}^{m -}

Gdzie $M^{x +}$ i $X^{m -}$ oznaczają odpowiednio kation i anion trudno rozpuszczalnego związku o wzorze $M_{m} X_{x}$ .

Wyrażenie na stałą równowagistałą równowagi tej reakcji możemy zapisać w postaci:

K = \frac{{[M^{x +}]}^{m} · {[X^{m -}]}^{x}}{[M_{m} X_{x}]}

${[M^{x +}]}^{m}$ – stężenie molowe jonów $M^{x +}$ w roztworze nasyconym;
${[X^{m -}]}^{x}$ – stężenie molowe jonów $X^{m -}$ w roztworze nasyconym;
$m$ – wartościowość reszty kwasowej (lub anionu wodorotlenkowego) równa liczbie kationów metalu;
$x$ – wartościowość metalu równa liczbie anionów reszt kwasowych (w przypadku soli) lub liczbie anionów wodorotlenkowych (w przypadku wodorotlenków).

Powyższe równanie oznacza, że w tym samym czasie tyle samo jonów przechodzi z fazy stałej do roztworu, ile się ich osadza na powierzchni osadu. W wyrażeniu tym stężenie osadu [ $M_{m} X_{x}$ ] jest wielkością stałą i przyjmuje wartość 1. Z tego względu stężenia ciał stałych w wyrażeniu na iloczyn rozpuszczalności można włączyć do stałej.

K \cdot [M_{m} X_{x}] = {[M^{x +}]}^{m} \cdot {[X^{m -}]}^{x}

K_{so} = {[M^{x +}]}^{m} \cdot {[X^{m -}]}^{x}

stała rozpuszczalności

Definicja: stała rozpuszczalności

$K_{so}$ (indeks so od ang. solubility „rozpuszczalność”) nazywana jest iloczynem rozpuszczalności,

K_{so} = [M^{x +}]^{m} \cdot [X^{m -}]^{x}

a wyrażenie $[M^{x +}]^{m} \cdot [X^{m -}]^{x}$ – iloczynem jonowym, który jest iloczynem stężeń molowych kationu i anionu podniesionych do odpowiednich potęg $m$ , $x$ , oznaczających współczynniki stechiometryczne z równania procesu rozpuszczania osadu trudno rozpuszczalnego.

Ważne!

Iloczyn rozpuszczalności $K_{so}$ (oznaczany czasem jako $I_{r}$ ) jest wartością stałą w określonych warunkach ciśnienia i temperatury oraz charakterystyczną dla danego układu. Wartości $K_{so}$ wyznaczane są doświadczalnie i zestawiane tabelarycznie do dalszego wykorzystania. Wartości iloczynów rozpuszczalności związków trudno rozpuszczalnych podawane są bez jednostek. Natomiast podczas obliczania stężenia jonów w roztworze (np. na podstawie iloczynu rozpuszczalności), jednostką stężenia jest $\frac{mol}{{dm}^{3}}$ .

R166aLLwESQCI

Źródło: Lipiec T., Szmal Z., Chemia Analityczna z Elementami Analizy Instrumentalnej, Warszawa 1980.

Porównując wartości iloczynów rozpuszczalności substancji dysocjujących na tę samą liczbę kationów i tę samą liczbę anionów, możemy w łatwy sposób stwierdzić, która substancja jest lepiej rozpuszczalna w wodzie. Im mniejsza wartość iloczynu rozpuszczalności, tym rozpuszczalność mniejsza. W ten sposób możemy szybko stwierdzić, że chlorek srebra ( $I_{r} = 1,6 \cdot 10^{- 10}$ ) jest lepiej rozpuszczalny od bromku srebra ( $I_{r} = 7,7 \cdot 10^{- 13}$ ). Nie powinniśmy jednak porównywać w ten sposób rozpuszczalności substancji o różnej budowie, np. ${SrCrO}_{4}$ i ${PbI}_{2}$ – pomimo znaczącej różnicy wartości iloczynów rozpuszczalności ( $I_{r} = 3,5 \cdot 10^{- 5}$ ; $I_{r} = 1,4 \cdot 10^{- 8}$ ) ich rozpuszczalności będą bowiem podobne (stężenia nasyconych roztworów wynoszą odpowiednio $1,5 \cdot 10^{- 3} \frac{mol}{{dm}^{3}}$ dla ${PbI}_{2}$ i $5,9 \cdot 10^{- 3} \frac{mol}{{dm}^{3}}$ dla ${SrCrO}_{4}$ ).

RSbS7SRP7mzkJ

Zdjęcie przedstawia szkiełko zegarkowe, na którym znajduje się pewna ilość żółtego proszku. — Próbka strąconego osadu jodku ołowiu( $II$ ) PbI₂
Źródło: Adam Rędzikowski, licencja: CC BY-SA 4.0.

R19xQqPfkLz18

Na zdjęciu jest probówka, w której mętny niebieski roztwór. — Zawiesina wodorotlenku miedzi( $II$ ) w roztworze
Źródło: Chemik2001, licencja: CC BY-SA 4.0.

Podsumowując, aby ocenić, która substancja jest lepiej lub gorzej rozpuszczalna, należy pamiętać, że wartość $K_{so}$ można porównywać do substancji o tym samym składzie jonowym (czyli do takich, które dysocjują na taką samą liczbę jonów).

bg‑turquoise

Kiedy wytrąca się osad?

Czy po zmieszaniu dwóch roztworów, zawierających jony soli (lub wodorotlenku), wytrąci się osad?

W sposób uproszczony można powiedzieć, że iloczyn rozpuszczalności $K_{so}$ wskazuje, jakie stężenia jonów należy osiągnąć, aby wytrącić osad. Istnieją trzy przypadki, z którymi spotykamy się w praktyce laboratoryjnej i obliczeniach chemicznych.

Iloczyn stężeń jonowych trudno rozpuszczalnego elektrolituelektrolitelektrolitu (podniesionych do odpowiednich potęg) jest mniejszy od jego iloczynu rozpuszczalności. Wówczas osad nie wytrąca się, a substancja całkowicie rozpuszcza się w wodzie (roztwór nienasyconyroztwór nienasyconyroztwór nienasycony).
$K_{SO} > {[M^{x +}]}^{m} \cdot {[X^{m -}]}^{x}$
Iloczyn stężeń jonów (podniesionych do odpowiednich potęg) trudno rozpuszczalnego elektrolitu równa się jego iloczynowi rozpuszczalności. Otrzymujemy roztwór nasyconyroztwór nasyconyroztwór nasycony, układ znajduje się w stanie równowagi dynamicznej.
$K_{SO} = {[M^{x +}]}^{m} \cdot {[X^{m -}]}^{x}$
Co istotne, stężenie jednego z jonów może przyjmować dowolną wartość, pod warunkiem, że stężenie drugiego jonu będzie takie, aby spełniona była powyższa zależność.
Gdy iloczyn stężeń jonowych trudno rozpuszczalnego elektrolitu (podniesionych do odpowiednich potęg) w roztworze jest większy od iloczynu rozpuszczalności, to należy spodziewać się wytrącenia nadmiaru substancji:
$K_{SO} < {[M^{x +}]}^{m} \cdot {[X^{m -}]}^{x}$
Wytrącenie substancji stałej spowoduje bowiem zmniejszenie stężeń obu jonów w roztworze, a w konsekwencji spadek iloczynu stężeń jonów (podniesionych do odpowiednich potęg) do wartości równej iloczynowi rozpuszczalności. Jednakże roztwór nadal będzie nasycony.

bg‑gray1 1

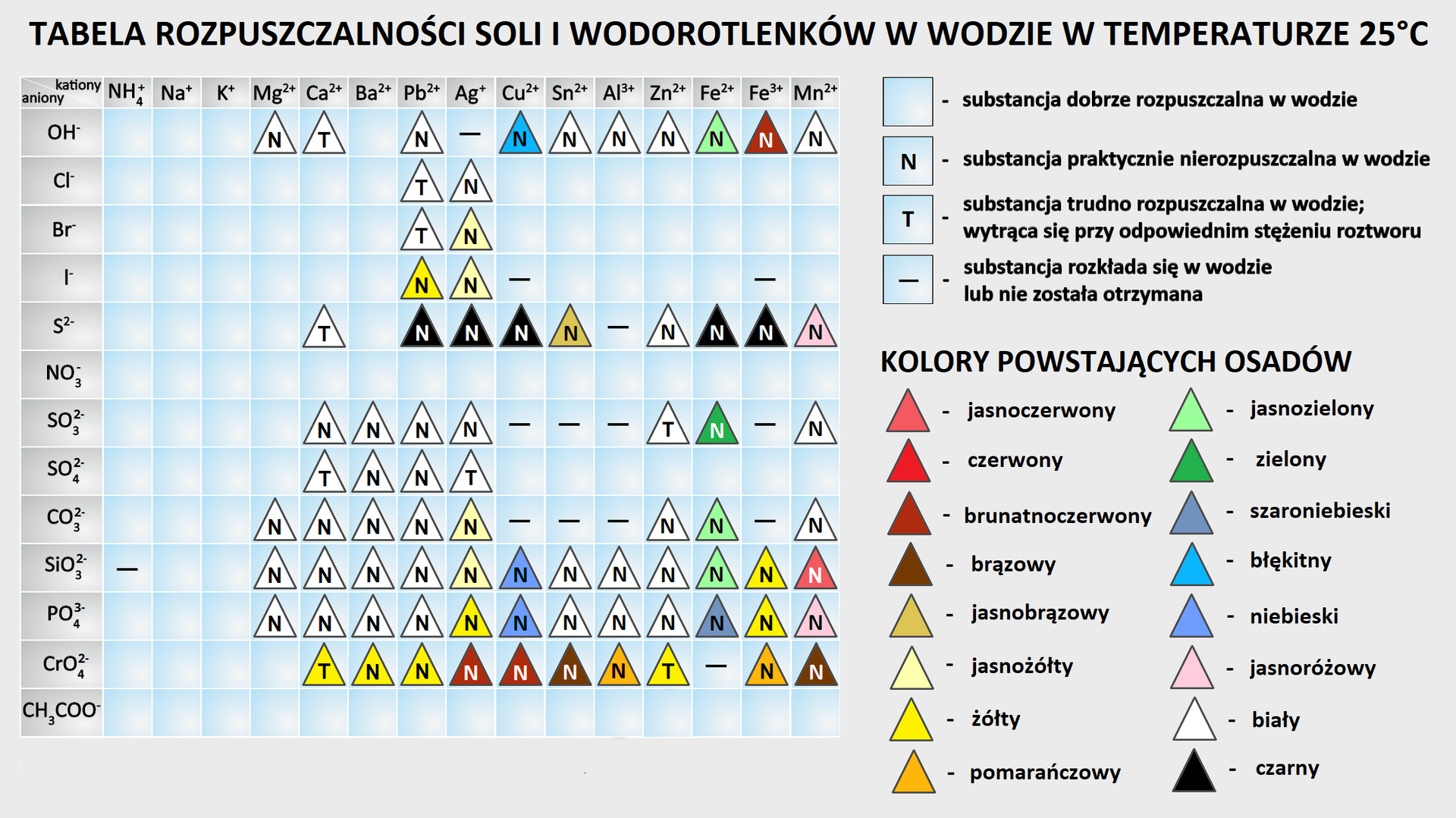
Podczas wytrącania osadów korzysta się z tabeli rozpuszczalności, w której znajdują się dane obrazujące charakter rozpuszczalności powstającego związku (osadu) w wodzie. Jeśli powstająca substancja jest:

rozpuszczalna – jej rozpuszczalność w wodzie jest większa niż 1 gram na 100 gramów wody;
trudno rozpuszczalna – strąca się w postaci osadu przy odpowiednim stężeniu roztworów (zazwyczaj z roztworów stężonych); jej rozpuszczalność w wodzie mieści się w granicach 0,1 – 1 grama na 100 gramów wody;
nierozpuszczalna – strąca się w postaci osadu z roztworów rozcieńczonych; jej rozpuszczalność w wodzie leży powyżej 0,1 grama na 100 gramów wody.

Indeks dolny /Źródło danych dotyczących wartości rozpuszczalności: wikipedia.org, data dostępu: 16.03.2020 r./ Indeks dolny koniec

RonQRibaRGxaE1

Tabela rozpuszczalności soli i wodorotlenków w wodzie w temperaturze dwudziestu pięciu stopni Celsjusza. Z tabeli można odczytać, które substancje są dobrze rozpuszczalne w wodzie, co symbolizuje pusta komórka, praktycznie nierozpuszczalne w wodzie, co symbolizuje litera N, trudno rozpuszczalne w wodzie, osad wytrąca się przy odpowiednim stężeniu roztworu, co symbolizuje litera T, substancje rozkładające się lub takie, dla których substancja chemiczna nie została otrzymana, co symbolizuje znak minusa. Ponadto zaznaczono kolory otrzymywanych osadów. Aniony wypisane w kolumnie: wodorotlenkowy, chlorkowy, bromkowy, jodkowy, siarczkowy, azotanowy(<math aria‑label="pięć">V), siarczanowy(<math aria‑label="cztery">IV), siarczanowy(<math aria‑label="sześć">VI), węglanowy, krzemianowy, fosforanowy(<math aria‑label="pięć">V), chromianowy(<math aria‑label="sześć">VI), octanowy. Kationy wypisane w wierszu: amonu, potasu, magnezu, wapnia, baru, ołowiu, srebra, miedzi, cyny, glinu, cynku, żelaza(<math aria‑label="dwa">II), żelaza (<math aria‑label="trzy">III), manganu, kobaltu. Wszystkie sole amonowe oraz wodorotlenki: amonowe, sodowe, potasowe oraz azotany(<math aria‑label="pięć">V) są rozpuszczalne w wodzie, oprócz krzemianu amonowego, który to oznaczono znakiem minus. Dla magnezu do nierozpuszczalnych należą białe: wodorotlenek magnezu, węglan magnezu, krzemian magnezu, fosforan(<math aria‑label="pięć">V) magnezu. Pozostałe sole magnezu zawarte w tabeli są rozpuszczalne. Dla wapnia do nierozpuszczalnych należą białe: siarczan(<math aria‑label="cztery">IV) wapnia, węglan wapnia, krzemian wapnia i fosforan(<math aria‑label="pięć">V) wapnia. Do trudno rozpuszczalnych należą białe: wodorotlenek wapnia, siarczek wapnia, siarczan(<math aria‑label="sześć">VI) wapnia oraz żółty chromian(<math aria‑label="sześć">VI) wapnia. Pozostałe sole wapnia są rozpuszczalne. Dla baru jako nierozpuszczalne i białe należą: siarczan(<math aria‑label="cztery">IV) baru, siarczan(<math aria‑label="sześć">VI) baru, węglan baru, krzemian baru oraz fosforan(<math aria‑label="pięć">V) baru, a także żółty chromian(<math aria‑label="sześć">VI) baru. Pozostałe są rozpuszczalne. Dalej oznaczono nierozpuszczalne i białe związki ołowiu: wodorotlenek ołowiu, siarczan(<math aria‑label="cztery">IV) ołowiu oraz siarczan(<math aria‑label="sześć">VI) ołowiu, węglan ołowiu, krzemian ołowiu oraz fosforan(<math aria‑label="pięć">V) ołowiu, a także czarny siarczek ołowiu oraz żółte sole: jodek ołowiu i chromian(<math aria‑label="sześć">VI) ołowiu. Do trudno rozpuszczalnych i białych związków ołowiu zaliczono chlorek ołowiu oraz bromek ołowiu. Pozostałe sole są dobrze rozpuszczalne. Dla srebra do nierozpuszczalnych zaliczono brązowy chromian(<math aria‑label="sześć">VI) srebra, białe sole: chlorek i siarczan(<math aria‑label="cztery">IV) srebra, żółtawe sole: bromek srebra, jodek srebra, węglan srebra, krzemian srebra, żółty fosforan(<math aria‑label="pięć">V) srebra, a także czarny siarczek srebra. Do trudno rozpuszczalnych soli srebra należą: biały siarczan(<math aria‑label="sześć">VI) srebra. Pozostałe sole są dobrze rozpuszczalne. Komórka z wodorotlenkiem srebra posiada znak minus. Dla miedzi do nierozpuszczalnych zaliczono niebieskie: wodorotlenek miedzi, krzemian miedzi oraz fosforan(<math aria‑label="pięć">V) miedzi, czarny siarczek miedzi oraz brązowy chromian(<math aria‑label="sześć">VI) miedzi. Pozostałe sole miedzi są rozpuszczalne, z wyjątkiem jodku miedzi, węglanu miedzi oraz siarczanu(<math aria‑label="cztery">IV) miedzi, które posiadają znak minus. Dla cyny na drugim stopniu utlenienia do nierozpuszczalnych zaliczono białe: wodorotlenek cyny, krzemian cyny oraz fosforan(<math aria‑label="pięć">V) cyny, brązowo‑żółty siarczek cyny i brązowy chromian(<math aria‑label="sześć">VI) cyny. Pozostałe są dobrze rozpuszczalne, z wyjątkiem siarczanu(<math aria‑label="cztery">IV) cyny oraz węglanu cyny, które oznaczono znakiem minus. Dla glinu do nierozpuszczalnych i białych zaliczono: wodorotlenek glinu, krzemian glinu, fosforan(<math aria‑label="pięć">V) glinu oraz pomarańczowy chromian(<math aria‑label="sześć">VI) glinu. Pozostałe sole są dobrze rozpuszczalne z wyjątkiem oznaczonych znakiem minus: siarczku, siarczanu(<math aria‑label="cztery">IV) i węglanu(<math aria‑label="cztery">IV). Dla cynku na drugim stopniu utlenienia do nierozpuszczalnych zaliczono białe: wodorotlenek cynku, siarczek cynku, węglan cynku, krzemian cynku, fosforan(<math aria‑label="pięć">V) cynku. Do trudno rozpuszczalnych związków cynku zalicza się biały siarczan(<math aria‑label="cztery">IV) cynku, a także żółty chromian(<math aria‑label="sześć">VI) cynku. Pozostałe związki cynku są rozpuszczalne. Dla żelaza na drugim stopniu utlenienia do nierozpuszczalnych zaliczono jasnozielone: wodorotlenek żelaza(<math aria‑label="dwa">II), węglan żelaza(<math aria‑label="dwa">II), krzemian żelaza(<math aria‑label="dwa">II), a także czarny siarczek żelaza(<math aria‑label="dwa">II), zielony siarczan żelaza(<math aria‑label="dwa">II) i niebieski fosforan(<math aria‑label="pięć">V) żelaza(<math aria‑label="dwa">II). Pozostałe sole żelaza(<math aria‑label="dwa">II) są dobrze rozpuszczalne, z wyjątkiem chromianu(<math aria‑label="sześć">VI) żelaza(<math aria‑label="dwa">II), który posiada symbol minusa. Dla żelaza na trzecim stopniu utlenienia do nierozpuszczalnych zaliczono: brązowy wodorotlenek żelaza(<math aria‑label="trzy">III), czarny siarczek żelaza(<math aria‑label="trzy">III), żółte krzemian żelaza(<math aria‑label="trzy">III) i fosforan(<math aria‑label="pięć">V) żelaza(<math aria‑label="trzy">III), a także pomarańczowy chromian(<math aria‑label="sześć">VI) żelaza(<math aria‑label="trzy">III). Pozostałe sole są rozpuszczalne, z wyjątkiem jodku żelaza(<math aria‑label="trzy">III), siarczanu(<math aria‑label="cztery">IV) żelaza(<math aria‑label="trzy">III) oraz węglanu żelaza(<math aria‑label="trzy">III), które posiadają symbol minusa. Dla manganu na drugim stopniu utlenienia wśród nierozpuszczalnych wyróżnia się białe: wodorotlenek manganu(<math aria‑label="dwa">II), siarczan(<math aria‑label="cztery">IV) manganu(<math aria‑label="dwa">II), węglan manganu(<math aria‑label="dwa">II), różowe: siarczek manganu(<math aria‑label="dwa">II) i fosforan(<math aria‑label="pięć">V) manganu(<math aria‑label="dwa">II), czerwony krzemian manganu(<math aria‑label="dwa">II), brązowy chromian(<math aria‑label="sześć">VI) manganu(<math aria‑label="dwa">II). Pozostałe sole są dobrze rozpuszczalne. — Tabela rozpuszczalności soli i wodorotlenków w wodzie
Źródło: GroMar Sp. z o.o., rozpuszczalność na podstawie: Mizerski W., *Tablice chemiczne*, Warszawa 2004; kolory osadów na podstawie: White W. E., *A Table of solubilities and colors of precipitates for use in a course in qualitative analysis*, „J. Chem. Educ.,” 1931., licencja: CC BY-SA 3.0.

Przykład 1

Obliczanie stężeń jonów ${Ba}^{2 +}$ oraz ${SO}_{4}^{2 -}$ w roztworze nasyconym siarczanu( $VI$ ) baru ${BaSO}_{4}$

Rozwiązanie:

Rozpuszczalność ${BaSO}_{4}$ w wodzie obrazuje poniższe równanie:

{BaSO}_{4 (s)} ⇄ {Ba}_{(aq)}^{2 +} + {SO}_{4 (aq)}^{2 -}

Jony pozostają z osadem w równowadze, a wyrażenie na iloczyn rozpuszczalności przyjmuje postać:

K_{SO} = [{Ba}^{2 +}] [{SO}_{4}^{2 -}]

R1B8cPdpBfSov

Ilustracja przedstawia zlewkę, w której jest roztwór, a na dnie znajduje się osad BaSO4. W roztworze nad osadem znajdują się liczne jony Ba2+ oraz towarzyszące im SO42−. — Uproszczony schemat równowagi pomiędzy osadem a roztworem na przykładzie siarczanu(VI) baru (BaSO₄)
Źródło: GroMar Sp. z o. o., licencja: CC BY-SA 3.0.

Wartość iloczynu rozpuszczalności $K_{so}$ w temperaturze 25°C dla siarczanu( $VI$ ) baru ( ${BaSO}_{4}$ ) wynosi $1, 1 \cdot 10^{- 10}$ .

Indeks dolny Źródło: Lipiec T., Szmal Z, Chemia Analityczna z Elementami Analizy Instrumentalnej, Warszawa 1980. Indeks dolny koniec

W wyniku rozpadu 1 mola ${BaSO}_{4}$ na jony powstaje 1 mol kationów baru i 1 mol anionów siarczanowych( $VI$ ), zatem można zapisać:

[{Ba}^{2 +}] = [{SO}^{2 -}_{4}]

K_{SO} = [{Ba}^{2 +}] [{SO}^{2 -}_{4}] = 1, 1 \cdot 10^{- 10}

Przyjmując stężenia jonów $[{Ba}^{2 +}] = [{SO}^{2 -}_{4}]$ , jako równe $x$ , otrzymujemy:

x^{2} = [{Ba}^{2 +}] [{SO}_{4}^{2 -}]

x^{2} = 1,1 \cdot 10^{- 10}

x = \sqrt{1,1 \cdot 10^{- 10}} = 1,05 \cdot 10^{- 5} [\frac{mol}{{dm}^{3}}]

Odpowiedź:

Stężenia jonów ${Ba}^{2 +}$ oraz ${SO}_{4}^{2 -}$ w roztworze nasyconym wynoszą 1,05 ∙ 10Indeks górny -5 $\frac{mol}{{dm}^{3}}$ .

Przykład 2

Czy po zmieszaniu $5 {cm}^{3}$ roztworu ${BaCl}_{2}$ o stężeniu $1 \cdot 10^{- 2} \frac{mol}{{dm}^{3}}$ oraz $5 {cm}^{3}$ roztworu ${Na}_{2} {SO}_{4}$ o stężeniu $1 \cdot 10^{- 5} \frac{mol}{{dm}^{3}}$ wytrąci się osad ${BaSO}_{4}$ ?

Rozwiązanie

Krok 1. Zapisanie równania reakcji:

Wyobraźmy sobie, że mieszamy ze sobą dwie substancje dobrze rozpuszczalne w wodzie ( ${BaCl}_{2}$ i ${Na}_{2} {SO}_{4}$ ), zawierające jony ${Ba}^{2 +}$ oraz ${SO}_{4}^{2 -}$ , w celu wytrącenia osadu ${BaSO}_{4}$ . W trakcie mieszania roztworów zachodzi reakcja opisana równaniem:

{Na}_{2} {SO}_{4} + {BaCl}_{2} \to {BaSO}_{4} + 2 NaCl

Lub w postaci uproszczonej:

{Ba}_{(aq)}^{2 +} + {SO}_{4 (aq)}^{2 -} \to {BaSO}_{4 (s)}

Po zmieszaniu roztworów ${Na}_{2} {SO}_{4}$ oraz ${BaCl}_{2}$ sumaryczna objętość roztworu wynosi 10 ${cm}^{3}$ . Zmianie ulegają stężenia roztworów, a co za tym idzie stężenia jonów.

Krok 2. Obliczenie stężeń jonów po zmieszaniu roztworów ${Na}_{2} {SO}_{4}$ i ${BaCl}_{2}$

1. ${BaCl}_{2}$ :

$C_{początkowe} (C_{1}) = 1 \cdot 10^{- 2} \frac{mol}{{dm}^{3}}$ - $C_{końcowe} (C_{2}) = ?$
$V_{początkowe} (V_{1}) = 5 {cm}^{3} = 0,005 {dm}^{3}$
$V_{końcowe} (V_{2}) = 10 {cm}^{3} = 0,010 {dm}^{3}$

Korzystamy ze wzoru na stężenie molowe:

C = \frac{n}{V}

Gdzie:

$C$ – stężenie;
$n$ – liczba moli;
$V$ – objętość roztworu.

Przyjmujemy, że:

n = C \cdot V

Bierzemy pod uwagę fakt, że liczba moli ${BaCl}_{2}$ przed zmieszaniem roztworów ( $n_{1}$ ) oraz po zmieszaniu roztworów ( $n_{2}$ ) nie ulega zmianie. Zmienia się wyłącznie objętość roztworu oraz jego stężenie. Zatem:

n_{1} = n_{2}

Stężenie końcowe roztworu ${BaCl}_{2}$ można obliczyć z zależności:

C_{1} \cdot V_{1} = C_{2} \cdot V_{2}

Po przekształceniu równania względem $C_{2}$ otrzymujemy:

C_{2} = \frac{C_{1} \cdot V_{1}}{V_{2}}

C_{2} = \frac{1 \cdot 10^{- 2} \frac{mol}{{dm}^{3}} \cdot 0,005 {dm}^{3}}{0,010 {dm}^{3}} = 5 \cdot 10^{- 3} \frac{mol}{{dm}^{3}}

${BaCl}_{2}$ dysocjuje zgodnie z równaniem:

{BaCl}_{2} \to {Ba}^{2 +} + {2 Cl}^{-}

Stężenie jonów ${Ba}^{2 +}$ jest równe stężeniu roztworu ${BaCl}_{2}$ :

[{BaCl}_{2}] = [{Ba}^{2 +}] = 5 \cdot 10^{- 3} \frac{mol}{{dm}^{3}}

2. ${Na}_{2} {SO}_{4}$ :

$C_{początkowe} (C_{1}) = 1 \cdot 10^{- 5} \frac{mol}{{dm}^{3}}$
$C_{końcowe} (C_{2}) = ?$
$V_{początkowe} (V_{1}) = 5 {cm}^{3} = 0,005 {dm}^{3}$
$V_{końcowe} (V_{2}) = 10 {cm}^{3} = 0,010 {dm}^{3}$

Podobnie obliczamy stężenie końcowe roztworu ${Na}_{2} {SO}_{4}$ :

C_{2} = \frac{C_{1} \cdot V_{1}}{V_{2}}

C_{2} = \frac{1 \cdot 10^{- 5} \frac{mol}{{dm}^{3}} \cdot 0,005 {dm}^{3}}{0,010 {dm}^{3}} = 5 \cdot 10^{- 6} \frac{mol}{{dm}^{3}}

${Na}_{2} {SO}_{4}$ dysocjuje zgodnie z równaniem:

{Na}_{2} {SO}_{4} \to {2 Na}^{+} + {SO}_{4}^{2 -}

Stężenie jonów ${SO}_{4}^{2 -}$ jest równe stężeniu roztworu ${Na}_{2} {SO}_{4}$ :

[{Na}_{2} {SO}_{4}] = [{SO}^{2 -}_{4}] = 5 \cdot 10^{- 6} \frac{mol}{{dm}^{3}}

Krok 3. Zapisanie wyrażenia na iloczyn rozpuszczalności $K_{so}$

Wartość iloczynu rozpuszczalności $K_{so}$ w temperaturze 25°C dla siarczanu( $VI$ ) baru ( ${BaSO}_{4}$ ) wynosi $1,1 \cdot 10^{- 10}$ .

Indeks dolny /Źródło: Lipiec T., Szmal Z., Chemia Analityczna z Elementami Analizy Instrumentalnej, Warszawa 1980./ Indeks dolny koniec

K_{so} = [{Ba}^{2 +}] [{SO}_{4}^{2 -}] = 1,1 \cdot 10^{- 10}

Do wytrącenia osadu ${BaSO}_{4}$ konieczne jest przekroczenie wartości iloczynu rozpuszczalności $K_{so}$ , Zatem iloczyn ze stężeń jonów ${Ba}^{2 +}$ i ${SO}_{4}^{2 -}$ musi być większy niż $K_{so}$ .

[{Ba}^{2 +}] [{SO}_{4}^{2 -}] > K_{so}

Obliczamy wartość iloczynu jonowego z warunków zadania, podstawiając stężęnia jonów z poprzedniego punktu (krok 2).

[{Ba}^{2 +}] [{SO}_{4}^{2 -}] = 5 \cdot 10^{- 3} \cdot 5 \cdot 10^{- 6} = 2,5 \cdot 10^{- 8}

[{Ba}^{2 +}] [{SO}_{4}^{2 -}] > K_{so}

Odpowiedź

Osad ${BaSO}_{4}$ wytrąci się, ponieważ został przekroczony iloczyn rozpuszczalności $K_{so}$ .

bg‑turquoise

Efekt wspólnego jonu

Rozpuszczalność ${BaSO}_{4}$ w czystej wodzie będzie większa niż rozpuszczalność ${BaSO}_{4}$ w roztworze ${Na}_{2} {SO}_{4}$ . Siarczan( $VI$ ) sodu dysocjując, dostarcza do roztworu jony ${SO}_{4}^{2 -}$ :

{Na}_{2} {SO}_{4} ⇄ 2 {Na}^{+} + {SO}_{4}^{2 -}

{BaSO}_{4} ⇄ {Ba}^{2 +} + {SO}_{4}^{2 -}

Jony te niejako zajmują miejsca przeznaczone dla jonów pochodzących z dysocjacji ${BaSO}_{4}$ . Można więc powiedzieć, że roztwór posiada określoną ilość miejsc przeznaczonych dla jonów pochodzących z dysocjacji ${BaSO}_{4}$ , czyli ${Ba}^{2 +}$ i ${SO}_{4}^{2 -}$ . Jeśli miejsca te zajmie ktoś inny, np. jony ${SO}_{4}^{2 -}$ pochodzące z innej substancji, to w konsekwencji mniejsza ilość ${BaSO}_{4}$ będzie mogła ulec rozpuszczeniu w takim roztworze. Takie zjawisko opisujemy jako efekt wspólnego jonu.

bg‑turquoise

Rozpuszczalność

Znajomość iloczynu rozpuszczalności pozwala na obliczenie rozpuszczalności danej substancji, a mianowicie rozpuszczalności molowej ( $S$ ) $[\frac{mol}{{dm}^{3}}]$ . Jest ona wyrażona jako liczba moli substancji, którą można rozpuścić w $1 {dm}^{3}$ roztworu. Rozpuszczalność molowa $S$ równa jest zatem całkowitemu stężeniu molowemu substancji rozpuszczonej w roztworze nasyconym tej substancji.

Przykład 3

Obliczanie rozpuszczalności molowej soli trudno rozpuszczalnej o znanym iloczynie rozpuszczalności

Oblicz rozpuszczalność molową soli ${Ag}_{2} S$ , której iloczyn rozpuszczalności wynosi $1, 6 \cdot 10^{- 49}$ .

Indeks dolny /Źródło danych K Indeks dolny koniecIndeks dolny s: Lipiec T., Szmal Z., Chemia Analityczna z Elementami Analizy Instrumentalnej, Warszawa 1980./ Indeks dolny koniec

Rozwiązanie

Równowagę pomiędzy stałym ${Ag}_{2} S$ a roztworem opisuje zależność:

{Ag}_{2} S_{(s)} ⇄ 2 {Ag}_{(aq)}^{+} + S_{(aq)}^{2 -}

Wyrażenie na iloczyn rozpuszczalności:

K_{so} = {[{Ag}^{+}]}^{2} [S^{2 -}] = 1,6 \cdot 10^{- 49}

Z równania rozpuszczania soli wynika, że rozpuszczeniu $S$ moli soli będzie towarzyszyć wprowadzenie do roztworu $S$ moli jonów $S^{2 -}$ oraz 2 $S$ moli jonów ${Ag}^{+}$ :

[{Ag}^{+}] = 2 S oraz [S^{2 -}] = S

Zatem po podstawieniu wartości $S$ do wyrażenia na iloczyn rozpuszczalności otrzymujemy:

K_{so} = {[2 S]}^{2} \cdot [S] = 4 S^{2} \cdot S = 4 S^{3}

Przekształcamy wrażenie względem $S$ , co daje:

S = \sqrt[3]{\frac{K_{s}}{4}}

S = \sqrt[3]{\frac{1,6 \cdot 10^{- 49}}{4}} = 3,4 \cdot 10^{- 17} \frac{mol}{{dm}^{3}}

Odpowiedź

Rozpuszczalność molowa soli o wzorze ${Ag}_{2} S$ wynosi $3, 4 \cdot 10^{- 17} \frac{mol}{{dm}^{3}}$ .

bg‑turquoise

Podsumowanie

Spójrz na mapę myśli dotyczącą iloczynu rozpuszczalności i zastanów się, co oznaczają umieszczone na niej pojęcia. W razie wątpliwości przejrzyj materiał ponownie.

Zapoznaj się z mapą myśli dotyczącą iloczynu rozpuszczalności i zastanów się, co oznaczają umieszczone na niej pojęcia. W razie wątpliwości przestudiuj materiał ponownie.

RNv3ggkWj0pPE1

Mapa myśli. Lista elementów: Nazwa kategorii: Iloczyn rozpuszczalności [italic]K[/][subscript]so[/]{color=#FF9999}Elementy należące do kategorii Iloczyn rozpuszczalności [italic]K[/][subscript]so[/]{color=#FF9999}Nazwa kategorii: substancje jonowe[br](sole, wodorotlenki){color=#66CCFF}Elementy należące do kategorii substancje jonowe[br](sole, wodorotlenki){color=#66CCFF}Nazwa kategorii: kationy[br]i aniony{color=#CCCC99}Elementy należące do kategorii kationy[br]i aniony{color=#CCCC99}Nazwa kategorii: iloczyn[br]stężeń[br]jonowych{color=#777777}Elementy należące do kategorii iloczyn[br]stężeń[br]jonowych{color=#777777}Nazwa kategorii: mniejszy od[br][italic]K[/][subscript]so[/] - roztwór[br]nienasycony{color=#99CC33}{value=19}Nazwa kategorii: większy od[br][italic]K[/][subscript]so[/] - nadmiar[br]jonów[br]wytrąca się[br]w postaci[br]osadu{color=#99CC33}{value=22}Nazwa kategorii: równy [italic]K[/][subscript]so[/] -[br]roztwór[br]nasycony{color=#99CC33}{value=19}Koniec elementów należących do kategorii iloczyn[br]stężeń[br]jonowych{color=#777777}Koniec elementów należących do kategorii kationy[br]i aniony{color=#CCCC99}Koniec elementów należących do kategorii substancje jonowe[br](sole, wodorotlenki){color=#66CCFF}Nazwa kategorii: stała wartość w[br]określonych warunkach[br]ciśnienia i temperaturyNazwa kategorii: im mniejsza wartość,[br]tym sól jest trudniej[br]rozpuszczalnaElementy należące do kategorii im mniejsza wartość,[br]tym sól jest trudniej[br]rozpuszczalnaNazwa kategorii: ten sam[br]skład[br]jonowy{color=#99CC33}Koniec elementów należących do kategorii im mniejsza wartość,[br]tym sól jest trudniej[br]rozpuszczalnaNazwa kategorii: wartości w tablicach[br]chemicznych{color=#777777}Nazwa kategorii: rozpuszczalność[br]molowa ([italic]S[/]){color=#66CCFF}Nazwa kategorii: nie posiada jednostki{color=#0099CC}Koniec elementów należących do kategorii Iloczyn rozpuszczalności [italic]K[/][subscript]so[/]{color=#FF9999}

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Słownik

stechiometryczna (stężeniowa) stała równowagi

stała równowagi, w której stężenia równowagowe są podniesione do potęg odpowiadającym współczynnikom stechiometrycznym

reakcja odwracalna

reakcja, która może zachodzić w obu kierunkach (w kierunku produktów lub substratów)

elektrolit

(gr. ḗlektron „bursztyn”, lytós „rozpuszczalny”) związek chemiczny, który ulega procesowi rozpadu na jony pod wpływem wody i jest zdolny do przewodzenia prądu elektrycznego; gdy jest całkowicie zdysocjowany, mówimy o elektrolicie mocnym

roztwór nasycony

roztwór, w którym w danych warunkach ciśnienia i temperatury zwykle nie da się rozpuścić większej ilości danej substancji

roztwór nienasycony

roztwór, którego stężenie substancji rozpuszczonej jest mniejsze niż rozpuszczalność tej substancji w danych warunkach ciśnienia i temperatury

Bibliografia

Encyklopedia PWN

Litwin M., Styka‑Wlazło Sz., Szymońska J., To jest chemia 1, Warszawa 2013.

Hejwowska S., Marcinkowski R., Staluszka J. Równowagi i procesy jonowe Chemia 3, Gdynia 2006.

Skoog D. A., West D. M., Holler J. F., Crouch S. R.: Podstawy Chemii Analitycznej, t. 1, Warszawa, 2006.

Minczewski J., Marczenko Z., Chemia analityczna. T.2. Chemiczne metody analizy ilościowej, Warszawa 2011, wyd. 10.

Schweda E., Chemia nieorganiczna tom 1 - wprowadzenie i analiza ilościowa, Wrocław 2014.

Sienko M. J., Plane R. A. Chemia podstawy i zastosowania, Warszawa 1999.

Pazdro K., Rola‑Noworyta A., Akademicki zbiór zadań z chemii ogólnej, Warszawa 2013.

Wprowadzenie

Film samouczek

Iloczyn rozpuszczalności

Kiedy wytrąca się osad?

Efekt wspólnego jonu

Rozpuszczalność

Podsumowanie

Słownik

Bibliografia