Optymalizacja algorytmów sortowania

W jednym z poprzednich e‑materiałów omawialiśmy zagadnienie optymalizacji algorytmów sortowaniasortowaniesortowania. Polega ona na doprowadzeniu do uzyskania możliwie najbardziej wydajnego algorytmu. W procesie optymalizacji staramy się zazwyczaj ograniczyć liczbę zbędnych operacji. Przekłada się to na zmniejszenie pamięciowej i czasowej złożoności obliczeniowej algorytmu.

Istotą optymalizacji algorytmów nie jest opracowywanie całkowicie nowych metod porządkowania danych, lecz usprawnianie mechanizmów już znanych. Cały proces ma jednak również pewien związek z tworzeniem alternatywnych algorytmów. Część spośród nich bazuje na gotowych rozwiązaniach bądź czerpie niektóre z ich elementów. Optymalizacja miewa zatem także własny wkład w nowe sposoby sortowania.

Alternatywne metody sortowania

Powody, dla których opracowuje się alternatywne metody sortowania, mogą być przeróżne – rozpoczynając od chęci zaprojektowania dobrego, zdatnego do użytku algorytmu, a kończąc na dążeniach do rozwiązania jakiegoś problemu matematycznego. Niezależnie od pobudek autorów, analizowanie oraz testowanie przedstawionych mechanizmów daje szansę na dokonanie ciekawych obserwacji oraz wyciągnięcia z nich wniosków (a może także przyczynić się do powstania kolejnego nietypowego algorytmu).

Alternatywne sposoby porządkowania danych dobrze jest poznać nawet wtedy, gdy algorytmy sortowania uważamy wyłącznie za narzędzia przydatne podczas pisania programów. Istnieje spore prawdopodobieństwo, że nietypowe, rzadziej stosowane i mniej znane metody okażą się zdatne do efektywnego wykorzystania w obecnych bądź przyszłych projektach. Z tego właśnie powodu przeanalizujemy trzy różne algorytmy porządkowania danych: algorytm kopcowy, naleśnikowy oraz bogosort.

Sortowanie kopcowe

Algorytm sortowania kopcowego (nazywanego też sortowaniem przez kopcowanie lub sortowaniem stogowym) jest algorytmem niestabilnym. Podczas jego wykonywania  konstruowany jest pojawiający się w nazwie kopiec, będący w rzeczywistości drzewem binarnymdrzewo binarnedrzewem binarnym.

Załóżmy, że chcemy posortować nierosnąco zbiór {5, 8, 4, 11, 6, 9, 1}. Pierwszy element umieszczamy na samej górze stogu (możemy go również nazwać korzeniem drzewa binarnego).

R13ksr2A7OJS7

Ilustracja przedstawia zbiór liczb: 5, 6, 4, 11, 6, 9, 1.
Poniżej w okręgu znajduje się liczba 5.

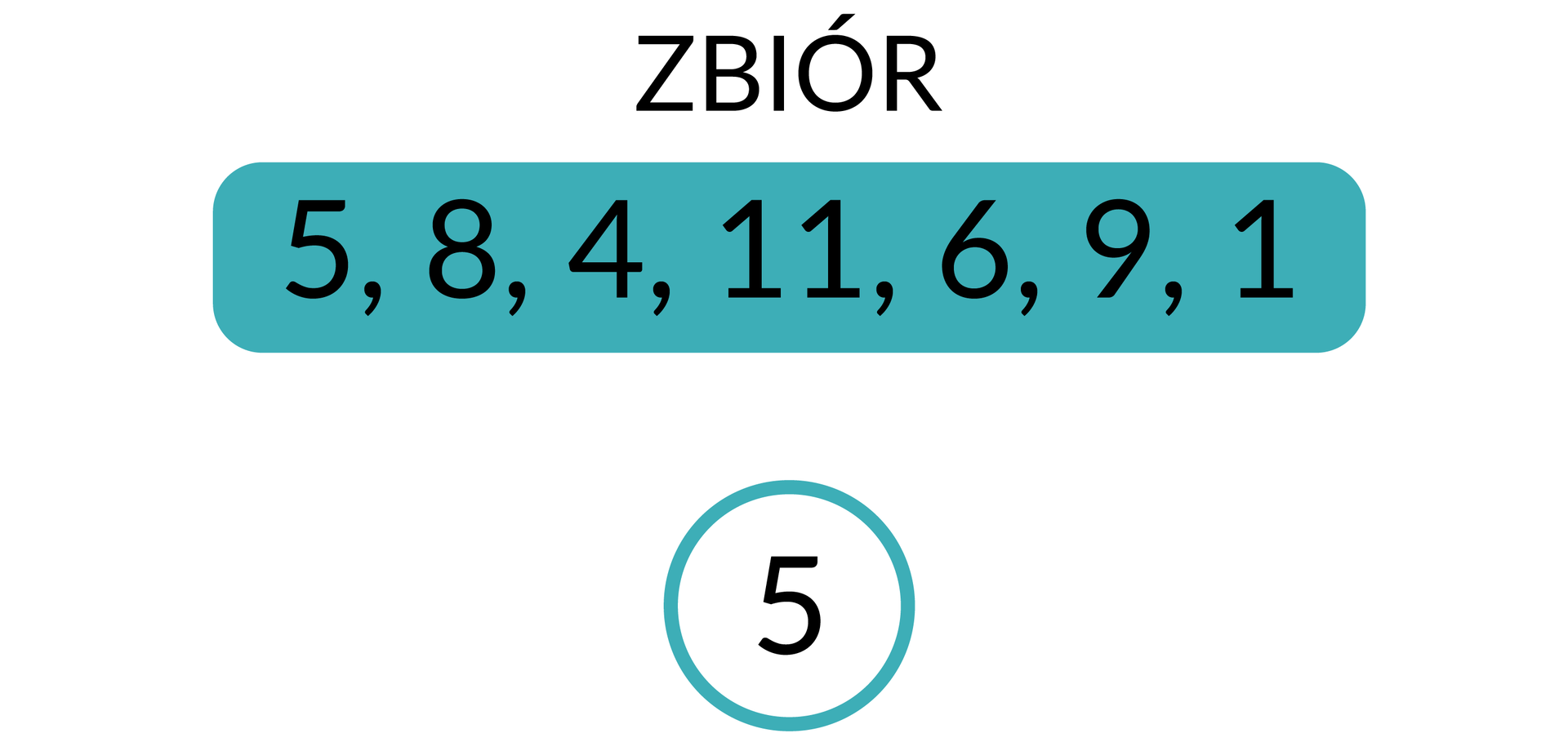
Poniżej szczytu kopca umieszczamy kolejny element zbioru. Porównujemy wartość górnego (tzw. nadrzędnego) węzła kopca z wartościami węzłów położonych niżej (tzw. potomnych węzłów kopca). Obowiązuje przy tym następująca zasada: jeżeli element znajdujący się na górze jest większy od elementu umieszczonego niżej, nie zmieniamy ich ułożenia. W przeciwnym przypadku zamieniamy elementy miejscami.

R15p0IZNtOP0z

Ilustracja przedstawia zbiór liczb: 5, 6, 4, 11, 6, 9, 1.
Poniżej w okręgu znajduje się liczba 5, wychodzi od niej prosta do liczby 8.

Liczba 8 jest większa niż 5, dlatego nastąpi zamiana miejsc.

R4vF4Rf7yS7OY

Ilustracja przedstawia zbiór liczb: 5, 6, 4, 11, 6, 9, 1.
Poniżej w okręgu znajduje się liczba 8, wychodzi od niej prosta do liczby 5.

Każdy węzeł nadrzędny ma dwa węzły potomne. Kolejny element zbioru umieścimy zatem na tym samym poziomie, na którym znajduje się obecnie element o wartości 5. Również i w tym wypadku sprawdzimy, czy zachowana jest przedstawiona wcześniej zasada.

RoIQGoylvEhPo

Ilustracja przedstawia zbiór liczb: 5, 6, 4, 11, 6, 9, 1.
Poniżej w okręgu znajduje się liczba 8, wychodzi od niej prosta do liczby 5 oraz 4.

Opisane czynności wykonujemy aż do wykorzystania wszystkich elementów zbioru. Na kolejnych obrazkach przedstawione zostały działania podejmowane przy dodawaniu liczby 11 do kopca.

R11rGwr4Nv4ju

Ilustracja przedstawia zbiór liczb: 5, 6, 4, 11, 6, 9, 1.
Poniżej w okręgu znajduje się liczba 8, wychodzi od niej prosta do liczby 5 oraz 4.
Z liczby 5 wychodzi prosta do liczby 11.

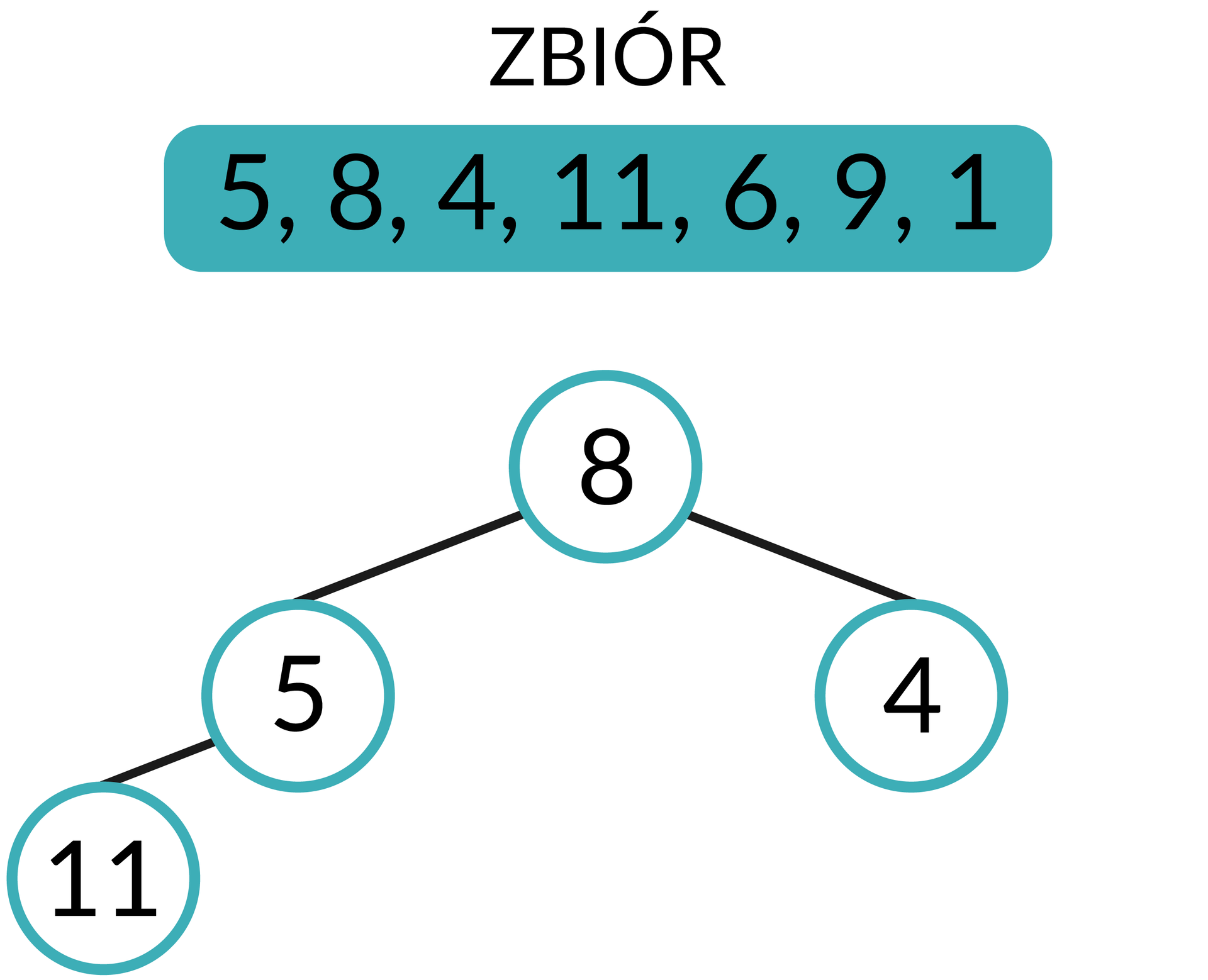
Liczba 11 jest większa od 5, musimy więc zamienić je miejscami.

RUqVMjSEpaRM1

Ilustracja przedstawia zbiór liczb: 5, 6, 4, 11, 6, 9, 1.
Poniżej w okręgu znajduje się liczba 8, wychodzi od niej prosta do liczby 5 oraz 4.
Z liczby 11 wychodzi prosta do liczby 5.

Liczba 11 jest również większa niż znajdująca się w węźle nadrzędnym liczba 8; ponownie zamieniamy więc elementy.

R1BwwViHdCrWX

Ilustracja przedstawia zbiór liczb: 5, 6, 4, 11, 6, 9, 1.
Poniżej w okręgu znajduje się liczba 11, wychodzi od niej prosta do liczby 8 oraz 4.
Z liczby 8 wychodzi prosta do liczby 5.

Po wykonaniu podobnych operacji na następnych elementach zbioru otrzymamy całe drzewo.

R1OPR4uqBZs4b

Ilustracja przedstawia zbiór liczb: 5, 6, 4, 11, 6, 9, 1.
Poniżej w okręgu znajduje się liczba 11, wychodzi od niej prosta do liczby 8 oraz 9.
Z liczby 8 wychodzi prosta do liczby 5 oraz 6.
Z liczby 9 wychodzą proste do licz 4 oraz 1.

Teraz należy zmienić budowę kopca. Popularną metodą jest przepisanie do pustego zbioru wartości elementu ze szczytu stogu, a następnie usunięcie go z kopca i zastąpienie ostatnim elementem (znajdującym się najdalej z prawej strony w najniższym rzędzie węzłów).

RVcBJhV6uDrUO

Ilustracja przedstawia zbiór liczb: 5, 6, 4, 11, 6, 9, 1.
Poniżej w okręgu znajduje się liczba 11, wychodzi od niej prosta do liczby 8 oraz 9.
Z liczby 8 wychodzi prosta do liczby 5 oraz 6.
Z liczby 9 wychodzą proste do licz 4 oraz 1.
Powyżej znajduje się tablica: Sortowanie.
W pierwszym polu umieszczono liczbę 11.

RmP5OzoKg7wtW

Ilustracja przedstawia zbiór liczb: Poniżej w okręgu znajduje się liczba 1, wychodzi od niej prosta do liczby 8 oraz 9.
Z liczby 8 wychodzi prosta do liczby 5 oraz 6.
Z liczby 9 wychodzą proste do licz 4 oraz 1.
Powyżej znajduje się tablica: Sortowanie.
W pierwszym polu umieszczono liczbę 11.

Musimy ponownie uporządkować stóg zgodnie z przedstawioną wcześniej zasadą. Po wykonaniu niezbędnych operacji na szczycie stogu znowu pojawi się największa obecnie liczba.

RBNM1kGmr3bzR

Ilustracja przedstawia zbiór liczb: Poniżej w okręgu znajduje się liczba 1, wychodzi od niej prosta do liczby 8 oraz 9.
Z liczby 8 wychodzi prosta do liczby 5 oraz 6.
Z liczby 9 wychodzi prosta do liczby 4.
Powyżej znajduje się tablica: Sortowanie.
W pierwszym polu umieszczono liczbę 11.
Na liczby 1 oraz 9 wskazują strzałki oznaczające zamianę.

RDBjlme1wFfOU

Ilustracja przedstawia zbiór liczb: Poniżej w okręgu znajduje się liczba 9, wychodzi od niej prosta do liczby 8 oraz 1.
Z liczby 8 wychodzi prosta do liczby 5 oraz 6.
Z liczby 1 wychodzi prosta do liczby 4.
Powyżej znajduje się tablica: Sortowanie.
W pierwszym polu umieszczono liczbę 11.
Na liczby 1 oraz 4 wskazują strzałki oznaczające zamianę.

RLZsZ4a5NCXMb

Ilustracja przedstawia zbiór liczb: Poniżej w okręgu znajduje się liczba 9, wychodzi od niej prosta do liczby 8 oraz 4.
Z liczby 8 wychodzi prosta do liczby 5 oraz 6.
Z liczby 4 wychodzi prosta do liczby 1.
Powyżej znajduje się tablica: Sortowanie.
W pierwszym polu umieszczono liczbę 11.

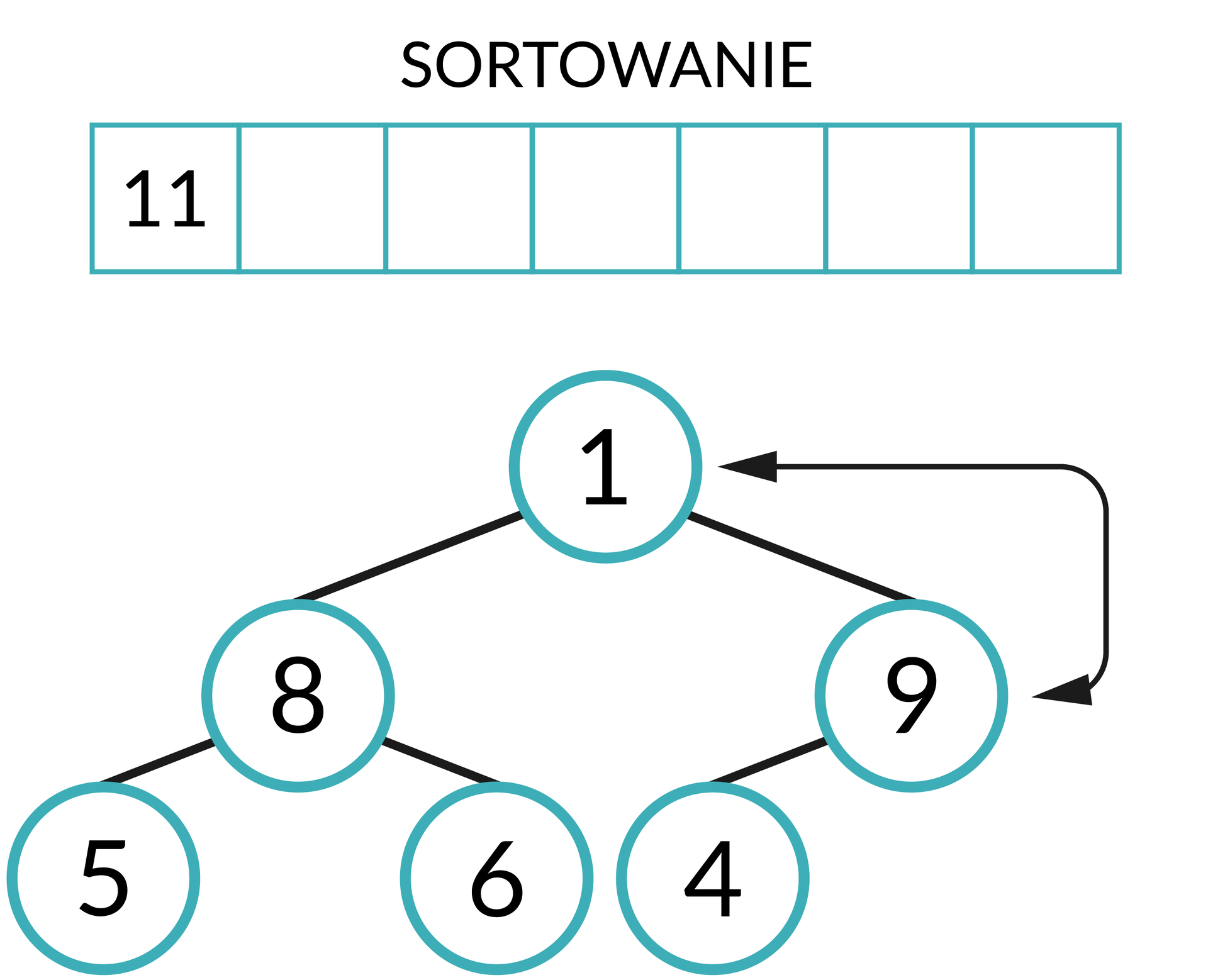
Czynności składające się na algorytm będziemy powtarzać do momentu, gdy wykorzystamy wszystkie węzły, a cały kopiec zniknie. Kolejne wartości umieszczane na szczycie kopca zapisujemy w zbiorze wynikowym przed ostatnio dodanymi elementami lub za nimi – w zależności od tego, czy chcemy posortować dane rosnąco, czy malejąco.

Warto zaznaczyć, że sortowanie przez kopcowanie jest efektywne pod względem pamięciowym oraz czasowym: jego pamięciowa i pesymistyczna czasowa złożoność obliczeniowa wynosi odpowiednio O(n) i O(n log n).

Sortowanie naleśnikowe

Sortowanie naleśnikowe, w przeciwieństwie do sortowania przez kopcowanie, nie jest typową metodą porządkowania danych, lecz raczej problemem matematycznym. Zakładamy, że dysponujemy kuchenną łopatką, za pomocą której musimy posortować ułożone jeden na drugim naleśniki o różnych rozmiarach. Wykorzystywany przyrząd możemy włożyć pomiędzy dwa dowolne naleśniki lub pod naleśnik znajdujący się na samym dole, a następnie przewrócić do góry nogami całą, znajdującą się nad łopatką stertę.

RbU8Wb310TmdJ

Ilustracja przedstawia osiem pomarańczowych poziomych słupków jeden na drugim symbolizujących naleśniki przed przewróceniem.
Każdy z tych słupków jest różnej długości.
Pomiędzy czwartym a piątym naleśnikiem znajduje się ciemna łopatka kuchenna.

RBWIMv5xe1UX5

Ilustracja przedstawia osiem pomarańczowych poziomych słupków leżących jeden na drugim symbolizujących naleśniki po przewróceniu.
Każdy słupek jest innej długości.
Pomiędzy czwartym a piątym naleśnikiem znajduje się ciemna łopatka kuchenna.
Naleśniki od piątego do ósmego zostały odwrócone kolejnością.

W odróżnieniu od typowego problemu związanego z sortowaniem nie interesuje nas liczba przeprowadzonych porównań, a jedynie minimalna liczba operacji łopatką wymagana do posortowania naleśników według ich rozmiaru. Bazując na liczbie naleśników, będziemy w stanie określić złożoność obliczeniową algorytmu. Jej analizę wykonamy dla prostej wersji sortowania naleśnikowego polegającej na wyszukiwaniu aktualnie największego, nieposortowanego jeszcze naleśnika i umieszczeniu go na szczycie stosu, a następnie wykonaniu kolejnego przewrócenia tak, aby naleśnik znalazł się na pożądanym miejscu.  Jako optymistyczny wariant sortowania założyć możemy scenariusz, w którym wszystkie naleśniki są od razu posortowane. Wówczas zbędne będą jakiekolwiek operacje łopatką, a złożoność czasowa wyniesie O(n) (n to liczba naleśników na stosie). W pesymistycznym przypadku na stercie ułożone będą na przemian kolejno naleśnik najmniejszy i największy. Wariant ten przedstawiony za pomocą zbioru liczb mógłby wyglądać następująco {0, 6, 1, 5, 2, 4, 3}. W takiej sytuacji wymagana liczba przewrotów naleśników określana jest jako 2n‑3, a również i sama złożoność czasowa ulegnie zmianie. Złożoność O(n) mogliśmy rozumieć jako czas wymagany na przewrócenie n naleśników. W przypadkach innych niż optymistyczny musimy jednak uwzględnić również czas przeznaczony na szukanie największego naleśnika. W wariancie pesymistycznym będziemy musieli przeszukiwać cały stos naszych naleśników przed wykonaniem operacji łopatką. Przy takim założeniu nasza złożoność czasowa wyniesie O(nIndeks górny 2²).

Dodatkowo warto nadmienić, że sortowanie naleśnikowe nie wymaga żadnej pamięci pomocniczej, dlatego złożoność pamięciowa określana jest jako O(n).

Bogosort

Bogosort (znany również jako slow sort lub stupid sort) jest algorytmem sortowania w pełni bazującym na losowości. Jego działanie jest proste w założeniach i polega na losowaniu ustawień sortowanych elementów, aż do uzyskania całkowicie posortowanego zbioru. Jest to metoda wysoce nieefektywna i nie nadaje się do praktycznego zastosowania. W wariancie pesymistycznym pełne posortowanie całego zbioru może nigdy nie nastąpić.

Wyobraźmy sobie następującą sytuację: przypadkowo ustawiamy wszystkich uczniów naszej szkoły w jednym rzędzie, a następnie pytam się każdego z nich po kolei o datę urodzenia. Szansa, że uda nam się uzyskać kolejność uczniów w rzędzie od najmłodszego do najstarszego jest niewyobrażalnie mała, nawet w przypadku, gdy nasza szkoła nie należy do największych placówek edukacyjnych. Tego typu przykład idealnie obrazuje nam wspomnianą nieefektywność algorytmu bogosort.

Opisywana metoda nie jest jednak całkowicie bezużyteczna. Może być dobrym, edukacyjnym porównaniem dla skuteczniejszych i popularniejszych metod sortowania.

Słownik