Przeczytaj
Miejscem zerowym funkcji nazywamy argument, dla którego wartość funkcji jest równa .
Zbiorem miejsc zerowych funkcji nazywamy zbiór wszystkich argumentów, dla których funkcja przyjmuje wartość .
Wiemy, że funkcję możemy opisywać różnymi sposobami. Poznamy sposoby wyznaczania miejsca zerowego funkcji w zależności od sposobu jej opisu. Pomogą nam w tym poniższe przykłady.
Funkcja opisana jest za pomocą grafu.
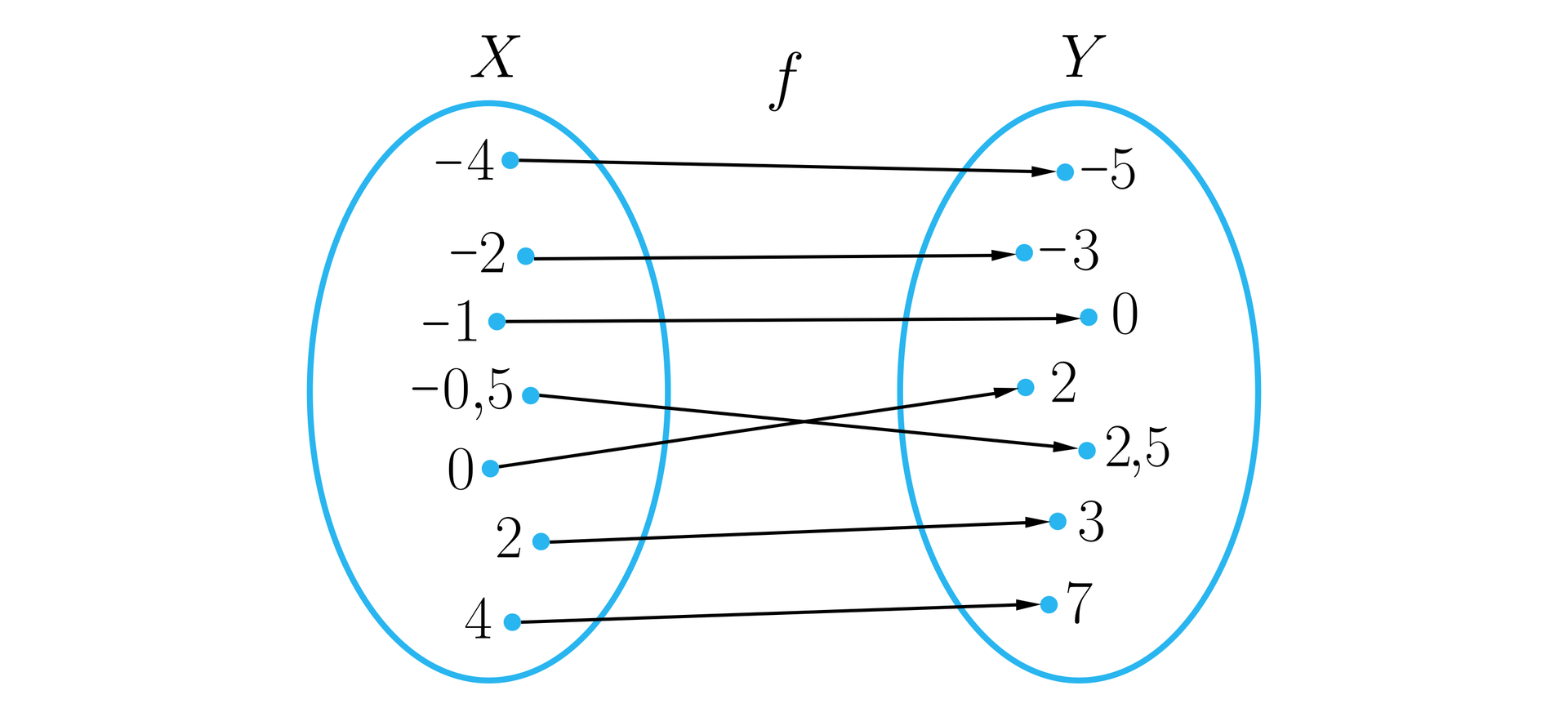
Wyznaczymy jej miejsce zerowe.
Rozwiązanie
Wśród wartości funkcji , które są umieszczone w prawej części grafu oznaczonej literą , szukamy liczby .
W następnym kroku przesuwamy się wzdłuż strzałki do lewej części grafu oznaczonej literą .
Liczba połączona jest z liczbą .
Stąd możemy zapisać, że miejscem zerowym funkcji jest liczba . Często miejsce zerowe oznaczamy . Możemy więc zapisać, że .
Funkcja opisana jest za pomocą tabelki.
Wyznaczymy jej miejsce zerowe.
Rozwiązanie
W drugim wierszu, oznaczonym symbolem , szukamy liczby .
Następnie w wierszu pierwszym, oznaczonym symbolem , szukamy odpowiedniego argumentu.
Jest nim liczba .
Stąd możemy zapisać, że miejscem zerowym funkcji jest liczba .
Zapisujemy to symbolicznie .
Funkcja przedstawiona jest za pomocą opisu słownego. Funkcja każdej liczbie rzeczywistej , takiej, że przyporządkowuje różnicę wartości bezwzględnej liczby i liczby .
Wyznaczymy jej miejsce zerowe.
Rozwiązanie
Przykład ten możemy rozwiązać dwoma sposobami.
Sposób pierwszy
Ponieważ do dziedziny należy tylko siedem liczb, to możemy wykonać tabelkę i z tabelki odczytać miejsce zerowe.
Zauważamy, że miejscem zerowym funkcji jest liczba .
Zapisujemy symbolicznie .
Sposób drugi
Zapiszemy funkcję za pomocą wzoru.
, gdy .
Rozwiążemy równanie .
lub .
Równanie jest spełnione przez dwie liczby i .
Sprawdzamy, która z liczb spełniających równanie, należy do dziedziny funkcji.
Do dziedziny funkcji należy liczba .
Stąd miejscem zerowym funkcji jest liczba .
Zapisujemy symbolicznie .
Funkcja opisana jest za pomocą zbioru par uporządkowanych.
Wyznaczymy miejsce zerowe funkcjimiejsce zerowe funkcji .
Rozwiązanie
Para uporządkowana jest postaci , tzn., że na pierwszym miejscu w każdej parze znajduje się element należący do dziedziny funkcji, a na drugim odpowiadająca temu elementowi wartość funkcji.
Wśród elementów zbioru par uporządkowanych wybieramy tę parę, w której na drugim miejscu jest .
Jest to para to para .
Stąd miejscem zerowym funkcji jest liczba .
Zapisujemy symbolicznie .
Ile miejsc zerowych może posiadać funkcja liczbowa?
Odpowiedź na to pytanie uzyskamy analizując kolejne przykłady.
Funkcja opisana jest za pomocą wzoru.
, gdy .
Wyznaczymy jej miejsce zerowe.
Rozwiązanie
Aby wyznaczyć miejsce zerowe funkcjimiejsce zerowe funkcji należy rozwiązać równanie i sprawdzić, czy otrzymane pierwiastki równania należą do dziedziny funkcji.
Otrzymaliśmy dwie liczby, które spełniają równanie .
Sprawdzamy, która z liczb należy do dziedziny funkcji .
Dziedziną funkcji jest przedział .
Zarówno liczba , jak i liczba należą do dziedziny funkcji.
Stąd wniosek, że funkcja ma dwa miejsca zerowe: i .
Zapisujemy to symbolicznie , .
Funkcja opisana jest za pomocą wykresu.

Wyznaczymy jej miejsce zerowe.
Rozwiązanie
Wykres funkcji przecina oś w trzech punktach: , , .
Funkcja ta ma trzy miejsca zerowe: , , .
Podsumujmy nasze wiadomości
Jeżeli funkcja opisana jest za pomocą grafu, to miejscem zerowym funkcji jest argument, należący do zbioru oznaczonego literą , który jest połączony strzałką z liczbą znajdującą się w zbiorze .
Jeżeli funkcja opisana jest za pomocą tabelki, to miejscem zerowym funkcji jest argument, zapisany w wierszu pierwszym, oznaczonym symbolem , któremu odpowiada wartość funkcji równa .
Jeżeli funkcja opisana jest za pomocą wzoru, to miejscem zerowym funkcjimiejscem zerowym funkcji jest pierwiastek równania wtedy, gdy należy on do dziedziny funkcji .
Jeżeli funkcja opisana jest za pomocą wykresu, to miejscem zerowym funkcji jest pierwsza współrzędna wykresu funkcji i osi .
Jeżeli funkcja opisana jest za pomocą zbioru par uporządkowanych, to miejscem zerowym funkcji jest liczba, zapisana na pierwszym miejscu w tej parze, w której na drugim miejscu znajduje się .
Czy każda funkcja liczbowa posiada miejsce zerowe?
W odpowiedzi na powyższe pytanie pomoże nam kolejny przykład.
Funkcja opisana jest za pomocą wykresu.

Wyznaczymy, o ile istnieje, miejsce zerowe funkcji .
Rozwiązanie
Wyznaczmy zbiór wartości funkcji .
Odczytujemy go na osi .
.
Możemy zauważyć, że .
Wynika z tego, że funkcja nie posiada miejsca zerowego.
Pamiętajmy, że funkcja będzie posiadała miejsce zerowe tylko wtedy, gdy do zbioru wartości tej funkcji będzie należała liczba .
Słownik
argument, dla którego wartość funkcji jest równa zero