Przesunięcia wykresu funkcji f(x)=a/x wzdłuż osi układu współrzędnych
Wiadomo, że wykres funkcji można przesuwać wzdłuż osi układu współrzędnych. W tej lekcji będziemy dokonywać tego przekształcenia na wykresie funkcji , czyli hiperboli.
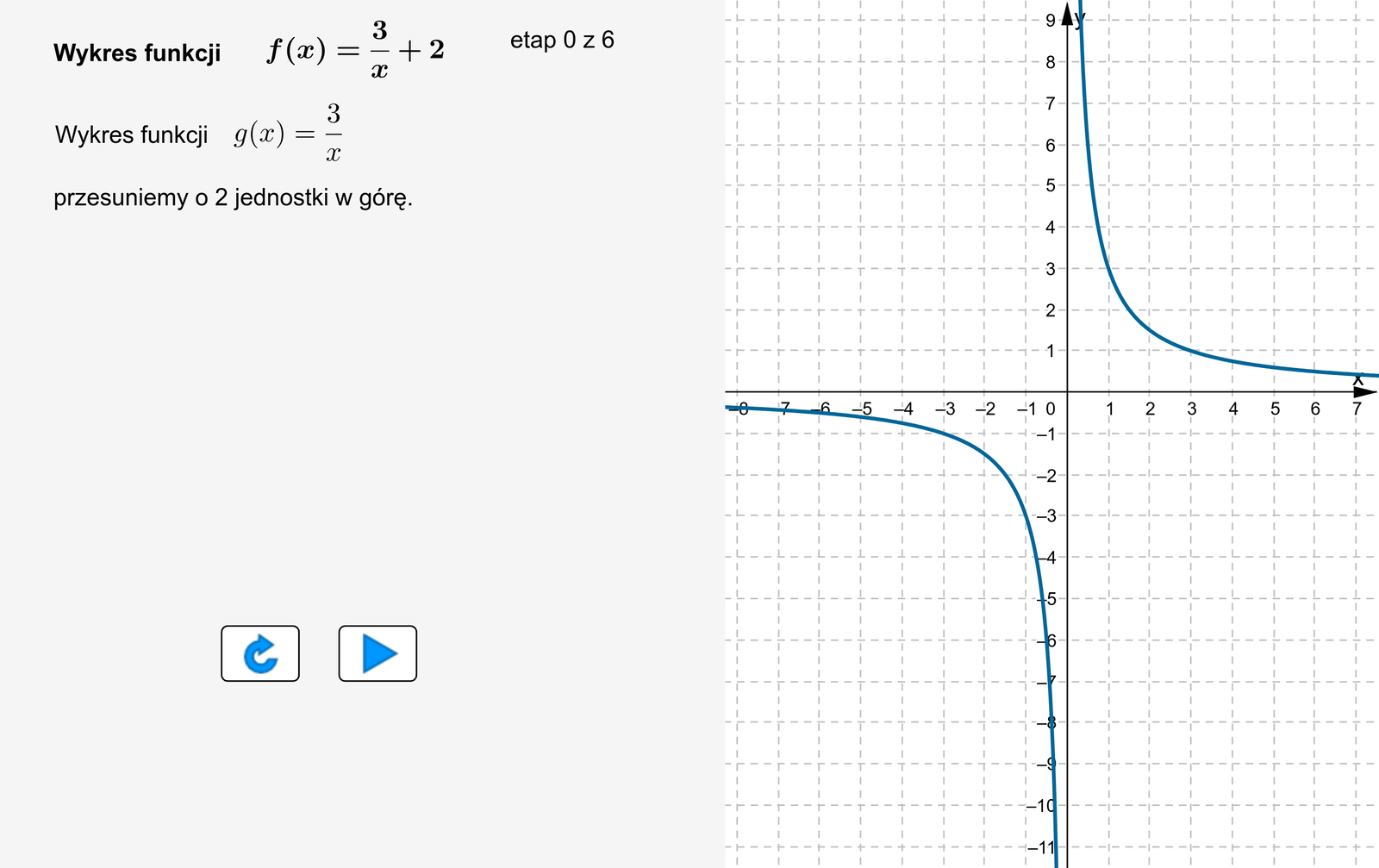
Narysujmy wykres funkcji .
Zauważmy, że do narysowania wykresu funkcji możemy wykorzystać hiperbolę . Jeśli przesuniemy ją o jednostki w górę wzdłuż osi , to otrzymamy wykres funkcji .
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PEPW2kMtu
Na podstawie wykresu omówmy własności funkcji .
Funkcja jest określona dla wszystkich (wykres funkcji nie przecina osi ).
Zbiorem wartości jest przedział .
Miejscem zerowym funkcji jest .
Funkcja jest malejąca w każdym z przedziałów oraz .
Funkcja przyjmuje wartości dodatnie dla argumentów ze zbioru oraz wartości ujemne dla argumentów z przedziału .
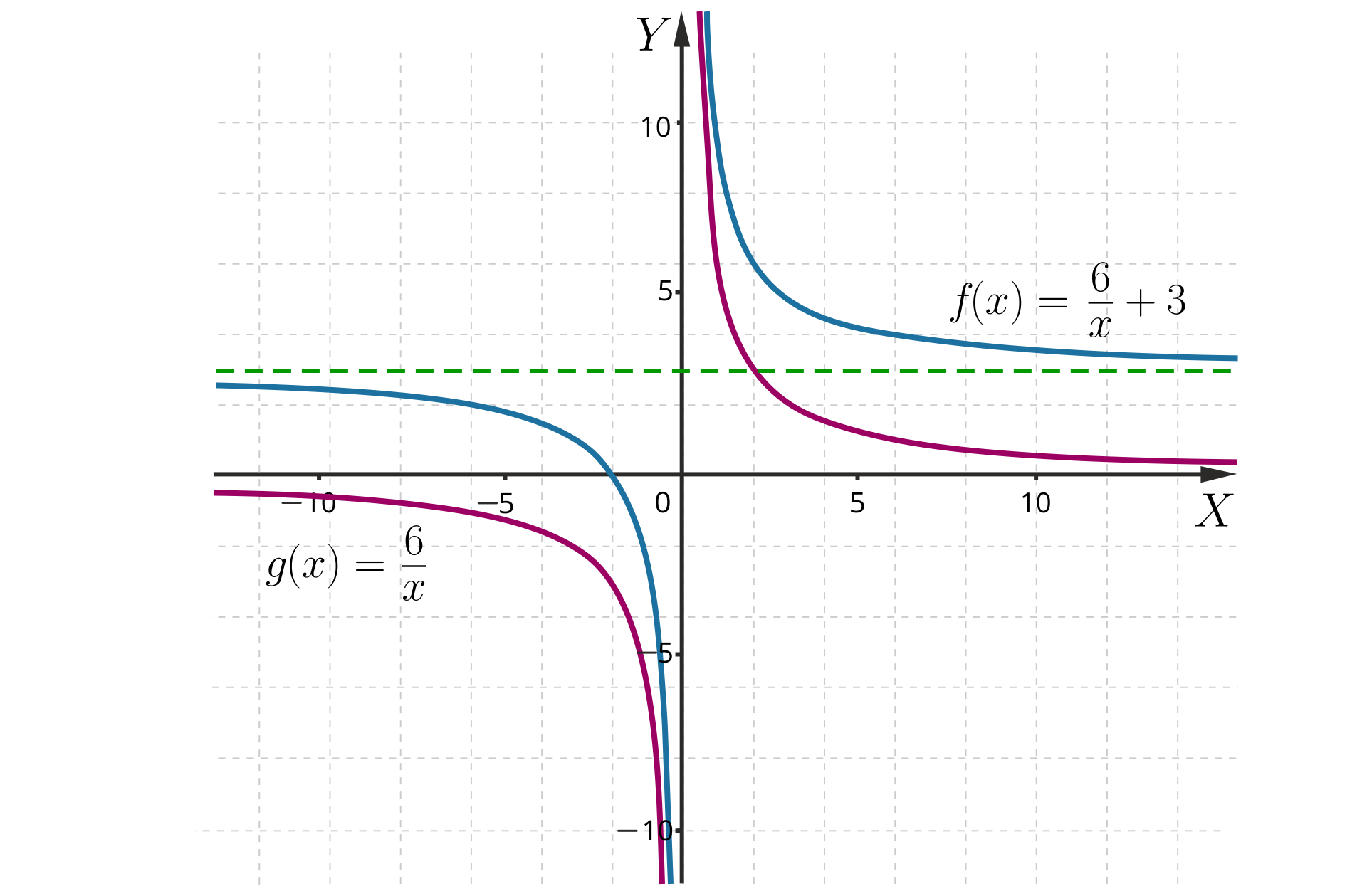
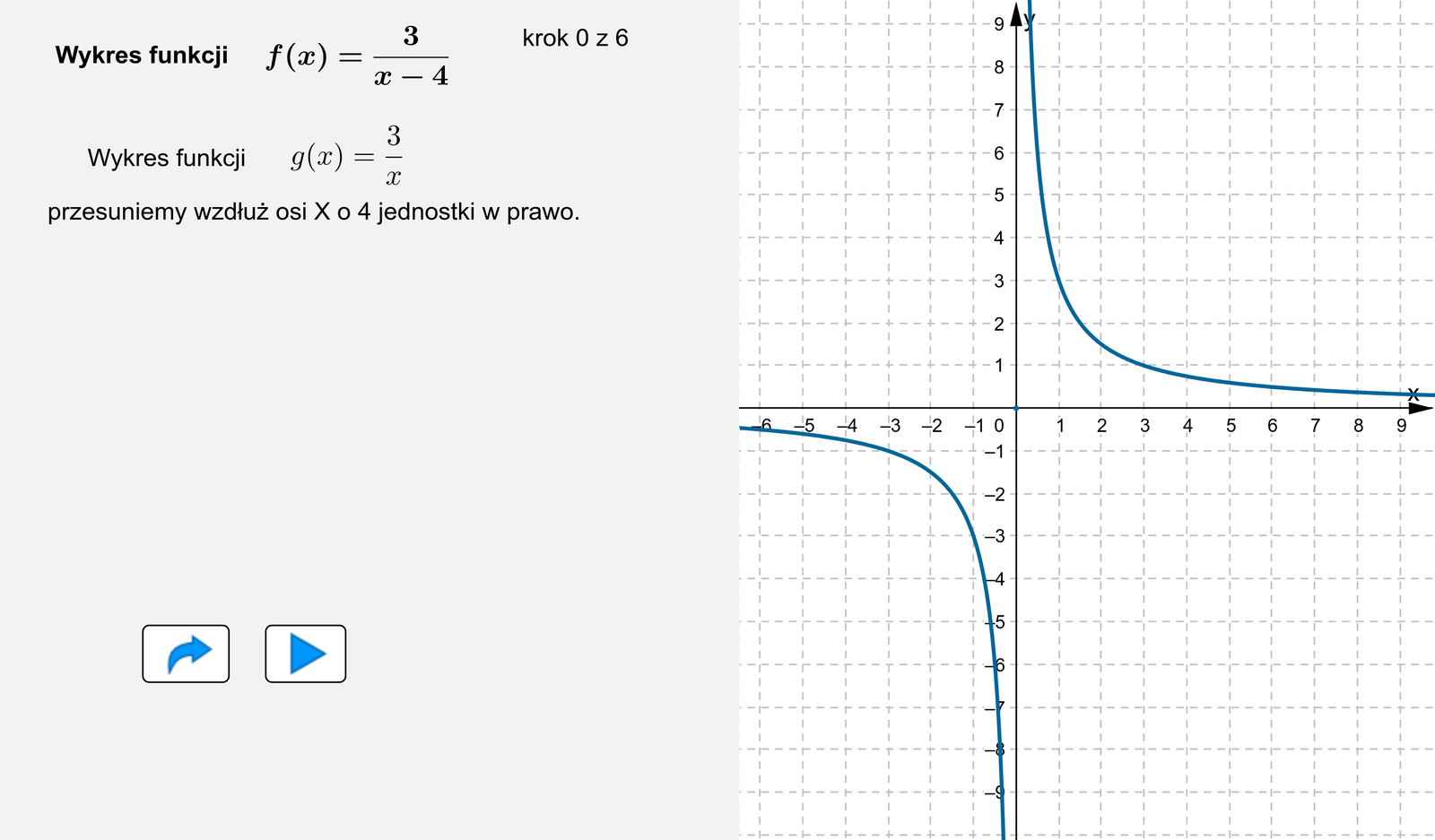
Narysujmy wykres funkcji .
Podobnie jak poprzednio do narysowania wykresu funkcji wykorzystamy hiperbolę . Jeśli przesuniemy ją o jednostki w prawo wzdłuż osi , to otrzymamy wykres funkcji .
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PEPW2kMtu
Na podstawie wykresu omówmy własności funkcji .
Funkcja jest określona dla argumentów z przedziału .
Zbiorem wartości jest przedział .
Funkcja nie ma miejsca zerowego.
Funkcja jest malejąca w każdym z przedziałów oraz .
Funkcja przyjmuje wartości dodatnie dla argumentów z przedziału oraz wartości ujemne dla argumentów z przedziału .
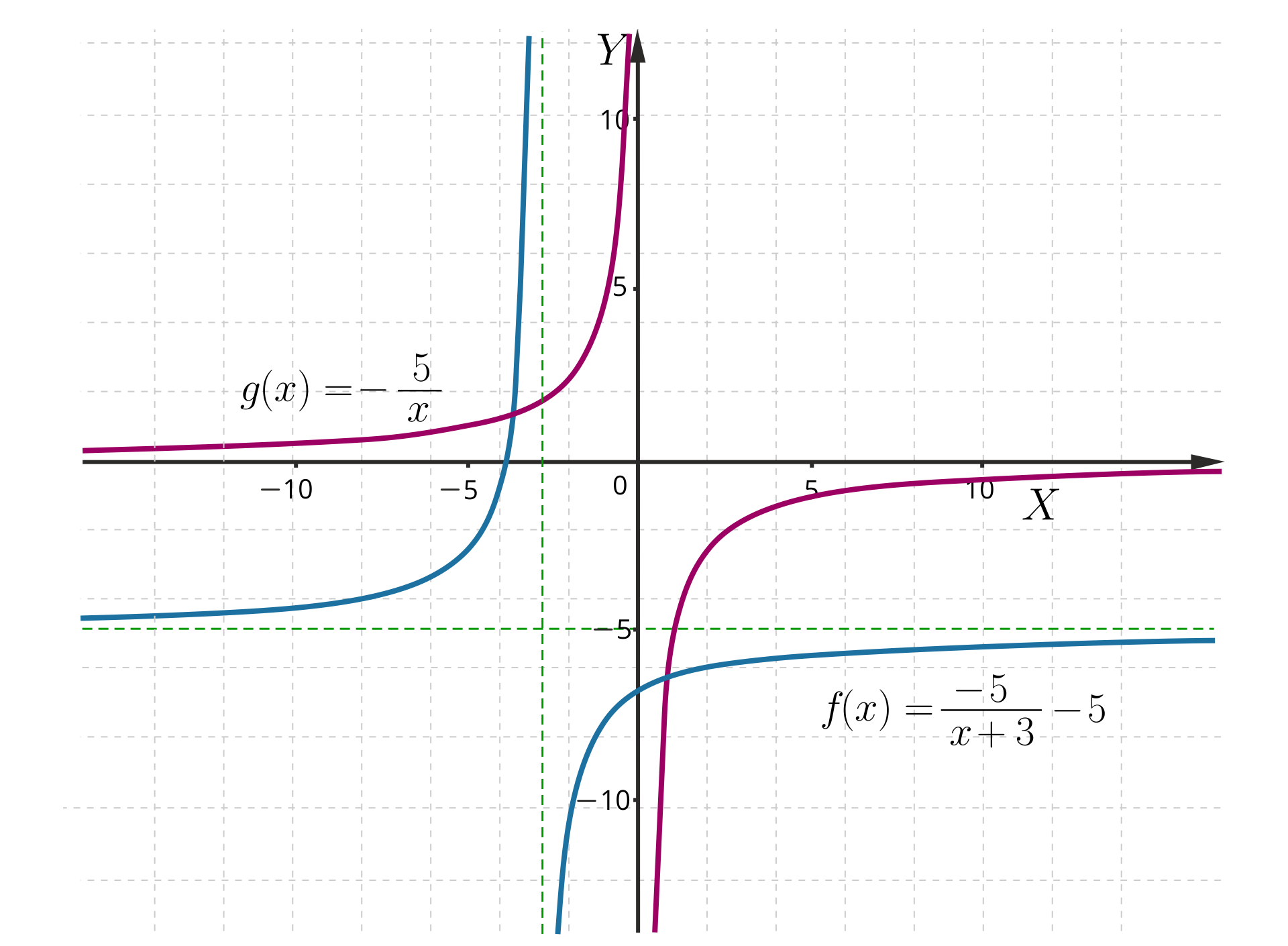
Narysujmy wykres funkcji .
Do narysowania tego wykresu wykorzystamy wykres funkcji i jego przesunięcie o jednostek w prawo wzdłuż osi i o jednostki w dół wzdłuż
osi .
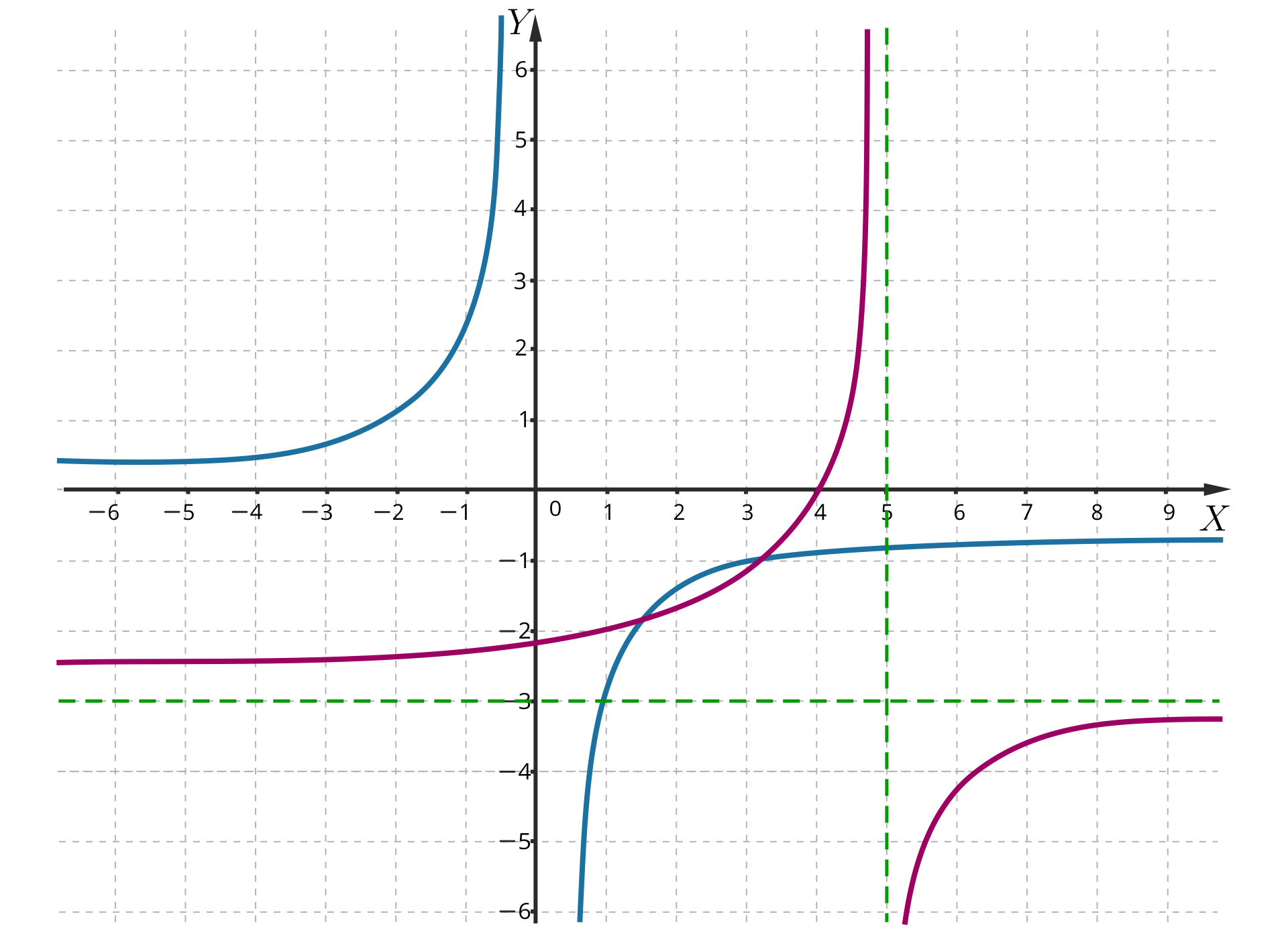
Z wykresu możemy odczytać własności funkcji .
Funkcja jest określona dla argumentów z przedziału .
Zbiorem wartości jest przedział .
Miejscem zerowym funkcji jest .
Funkcja jest rosnąca w każdym z przedziałów oraz .
Funkcja przyjmuje wartości dodatnie dla argumentów z przedziału oraz wartości ujemne dla argumentów ze zbioru .
Uruchom aplet i wykonaj polecenia w nim zawarte. Przesuwaj zielony punkt tak, aby otrzymać żądane wykresy funkcji o określonych dziedzinach i zbiorach wartości. Zwróć uwagę, że zarówno dziedzina, jak i zbiór wartości funkcji wyznaczą asymptoty nowej funkcji.
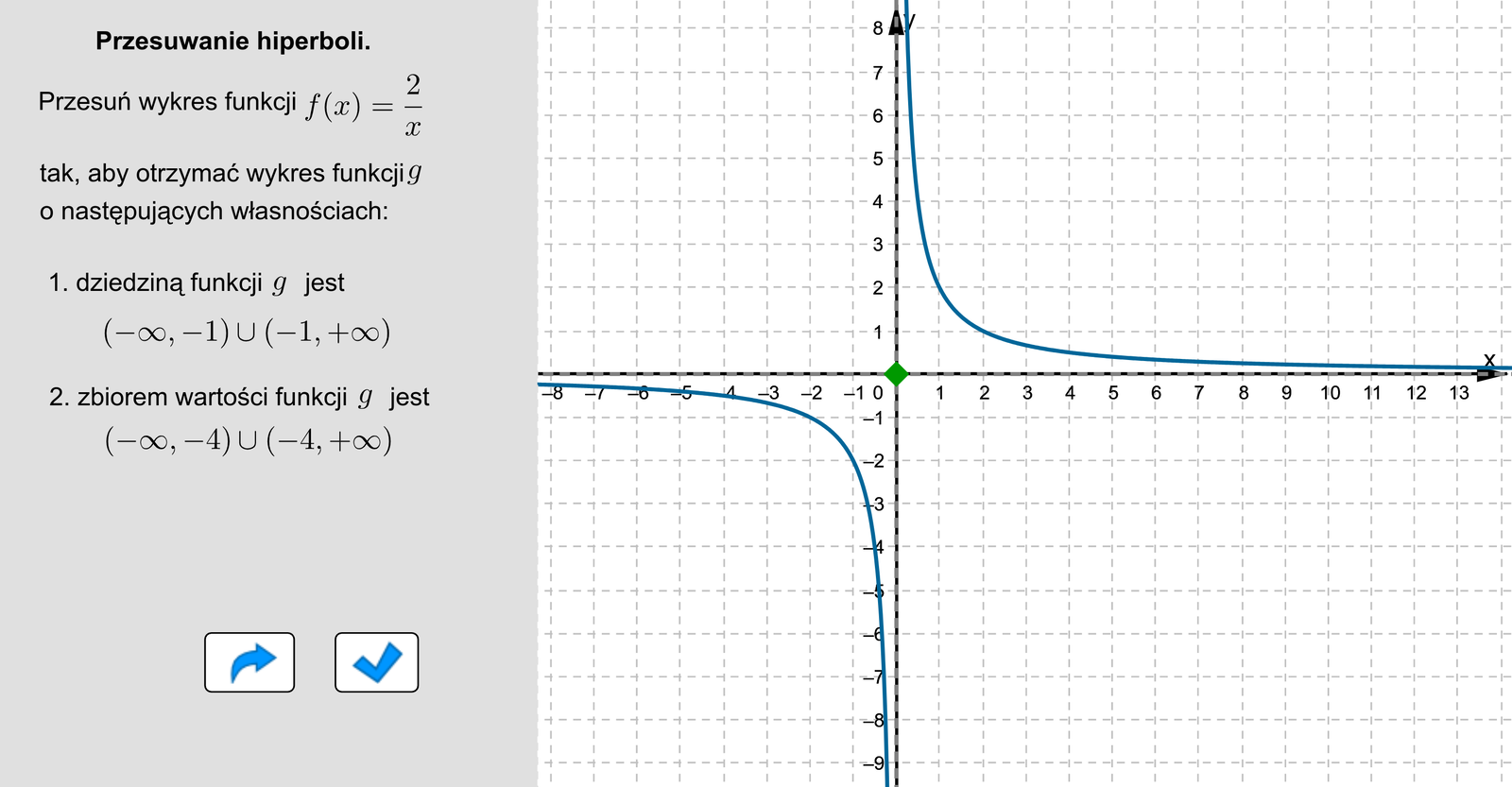
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PEPW2kMtu
Uzupełnij odpowiedzi na poniższe pytania, przeciągając w luki odpowiednie wyrażenia lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej.
Naszkicuj wykres funkcji . Określ, dla jakich argumentów funkcja przyjmuje wartości nieujemne.
Opisz wygląd wykresu funkcji . Określ, dla jakich argumentów funkcja przyjmuje wartości nieujemne.
Naszkicuj wykres funkcji . Określ jej dziedzinę i zbiór wartości. Dla jakich argumentów funkcja przyjmuje wartości mniejsze od ?
Opisz wygląd wykresu funkcji . Określ jej dziedzinę i zbiór wartości.
Dla jakich argumentów funkcja przyjmuje wartości mniejsze od ?
Określ dziedzinę i zbiór wartości funkcji opisanej wzorem
Funkcja opisana jest wzorem . Wyznacz wartość , dla której funkcja nie ma punktów wspólnych z prostą o równaniu .