Przykłady zasady zachowania energii mechanicznej

RazOwv1PFP9sP

Zasada zachowania energiizasada zachowania energiiZasada zachowania energii mechanicznej to jedno z podstawowych praw fizycznych. Została sformułowana już w $XVIII$ wieku. Zakłada ona, że wartości energii mogą się zmieniać, ale całkowita energia pozostaje stała, jeśli żadne siły zewnętrzne nie wykonują pracy nad rozpatrywanym układem ciał. Energia może zmieniać swoją formę i przekształcać się np. z kinetycznej w potencjalną. Jaki wpływ na energię ciał mają zderzenia sprężyste i niesprężyste? Dowiesz się z tego materiału.

Twoje cele

opiszesz, jakie mogą być rodzaje energii mechanicznej;
uporządkujesz wiadomości dotyczące zasady zachowania energii;
zdefiniujesz, czym są zderzenia sprężyste i niesprężyste;
obliczysz zmiany energii na wybranych przykładach;

Przeczytaj

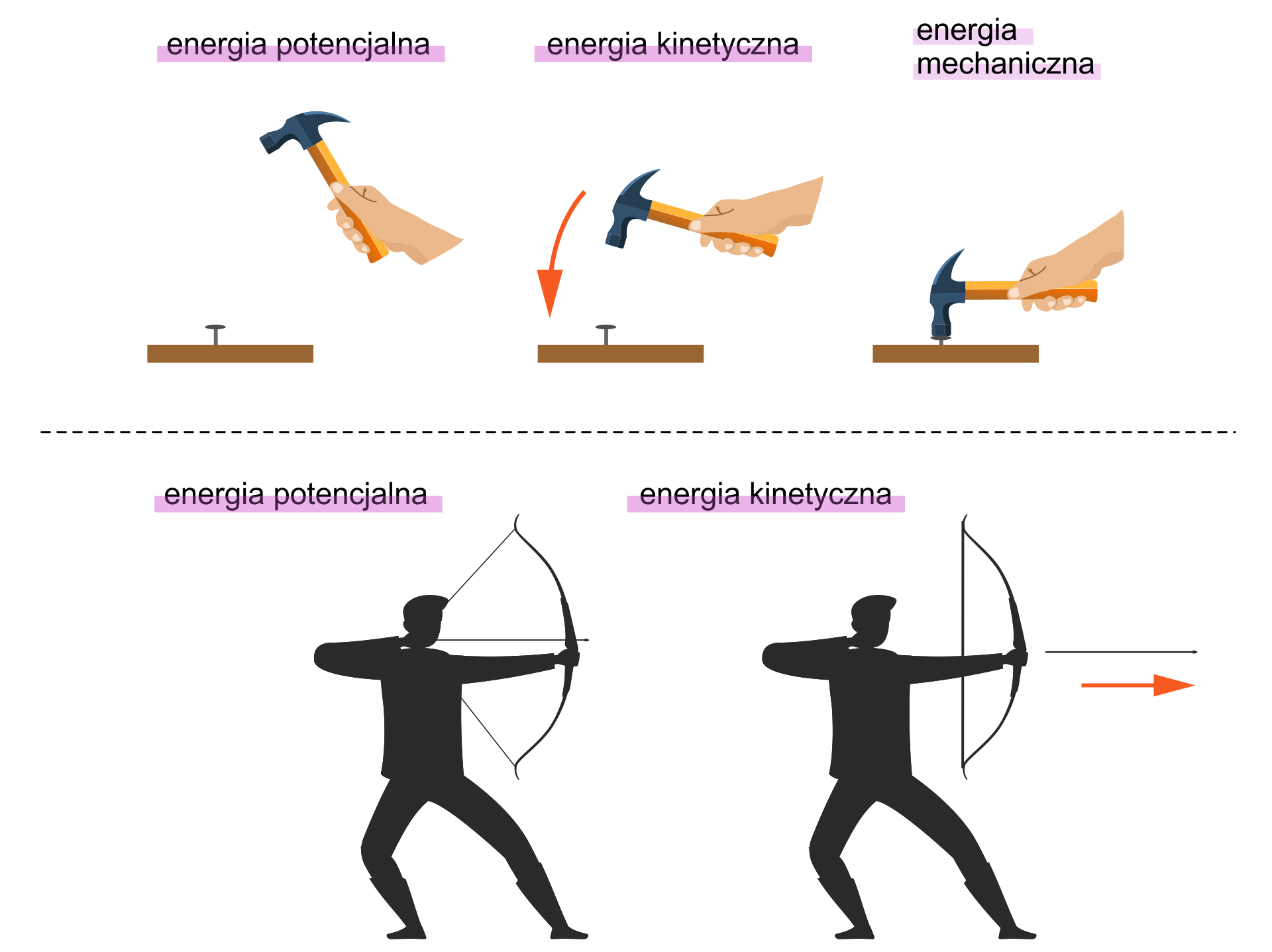
Do tej pory poznałeś podstawowe rodzaje energii mechanicznej – energię kinetyczną i potencjalną. Energia kinetyczna związana jest z ruchem ciała i zależy od jego prędkości. Energia potencjalna może być energią potencjalną grawitacji – zależna jest wtedy od względnego położenia ciała i wynika z działania siły grawitacji – lub energią potencjalną sprężystości – wynika wtedy z działania siły sprężystości. Wyrażamy je następującymi wzorami:

energia kinetyczna:
$E_{k} = \frac{m \cdot v^{2}}{2}$ ,
gdzie:
$m$ – masa,
$v$ – prędkość;

energia potencjalna grawitacji:
$E_{pg} = m \cdot g \cdot h$ ,
gdzie:
$m$ – masa,
$g$ – przyspieszenie ziemskie,
$h$ – wysokość;

energia potencjalna sprężystości:
$E_{ps} = \frac{k \cdot x^{2}}{2}$ ,
gdzie:
$k$ – współczynnik sprężystości,
$x$ – odkształcenie ciała.

Energie te mogą przechodzić jedna w drugą, ale energia mechaniczna całego układu jest zachowana zgodnie z zasadą zachowania energii.

R3wPGSHgNp19U

Ilustracja składa się z dwóch części. W części górnej widoczna jest dłoń z młotkiem, którym wbijany jest w płaską poziomą powierzchnię gwóźdź. Obrazek pierwszy. Energia potencjalna. Dłoń trzyma młotek w górze. Poniżej gwóźdź wystający z powierzchni. Obrazek drugi. Energia kinetyczna. Dłoń z młotkiem opada, główką młotka w kierunku gwoździa. Obrazek trzeci. Energia mechaniczna. Główka młotka uderza w gwóźdź. W dolnej części łucznik strzelający z łuku. Pierwszy obrazek. Energia potencjalna. Łucznik trzyma łuk z założoną strzałą i napiętą cięciwą. Drugi obrazek. Energia kinetyczna. Łucznik puścił cięciwę, strzała leci. — Różne rodzaje energii mogą przechodzić w inne, ale energia mechaniczna układu pozostaje zachowana
Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Przykład 1

Oblicz prędkość, jaką uzyska kamień na wysokości $2$ metrów po wystrzeleniu z procy. Masa kamienia wynosi $5 g$ , proca została naciągnięta o $25 cm$ , a współczynnik sprężystości procy wynosi $13, 2 \frac{N}{m}$ . Załóż, że wystrzelenie kamienia jest bezstratne i jest on wystrzeliwany z wysokości $1$ metra.

Rozwiązanie:

W opisanej sytuacji przed wystrzeleniem kamienia, posiada on energię potencjalną grawitacji i energię potencjalną sprężystości, a w interesującym nas momencie energię potencjalną grawitacji i energię kinetyczną. Z zasady zachowania energii wynika:

$E_{pg 1} + E_{ps} = E_{pg 2} + E_{k}$

a zatem:

$m \cdot g \cdot h_{1} + \frac{k \cdot x^{2}}{2} = m \cdot g \cdot h_{2} + \frac{m \cdot v^{2}}{2}$

po przemnożeniu stronami przez $2$ otrzymujemy:

$2 \cdot m \cdot g \cdot h_{1} + k \cdot x^{2} = 2 \cdot m \cdot g \cdot h_{2} + m \cdot v^{2}$

przekształcamy wzór aby obliczyć prędkość:

$2 \cdot m \cdot g \cdot h_{1} + k \cdot x^{2} - 2 \cdot m \cdot g \cdot h_{2} = m \cdot v^{2}$

$2 \cdot m \cdot g (h_{1} - h_{2}) + k \cdot x^{2} = m \cdot v^{2}$

$2 \cdot g (h_{1} - h_{2}) + \frac{k \cdot x^{2}}{m} = v^{2}$

a zatem:

$v = \sqrt{2 \cdot g (h_{1} - h_{2}) + \frac{k \cdot x^{2}}{m}}$

po wstawieniu wartości liczbowych obliczamy prędkość:

$x = 25 cm = 0, 25 m$

$k = 13, 2 \frac{N}{m} = 13, 2 \frac{kg}{s^{2}}$

$m = 5 g = 0, 005 kg$

$h_{1} = 1 m$

$h_{2} = 2 m$

$g = 10 \frac{m}{s^{2}}$

$v = \sqrt{2 \cdot 10 \frac{m}{s^{2}} (1 m - 2 m) + \frac{13, 2 \frac{kg}{s^{2}} \cdot {(0, 25 m)}^{2}}{0, 005 kg}} = \sqrt{- 20 \frac{m^{2}}{s^{2}} + 165 \frac{m^{2}}{s^{2}}} = 12 \frac{m}{s}$

Zderzenie jest pojęciem powszechnie używanym w życiu codziennym. Pełni ono ważną rolę również w fizyce. Zderzenie to zjawisko występujące, gdy jedno ciało będące w ruchu styka się gwałtownie z innym ciałem. Nie wszystkie takie oddziaływania są jednakowe i mogą mieć zupełnie inny charakter. Efektem zderzenia może być rozpadnięcie się ciała na wiele elementów, dwa ciała mogą połączyć się w jedno lub ciała mogą odbijać się od siebie. Wyróżnia się zderzenia sprężyste i niesprężyste oraz centralne i niecentralne.

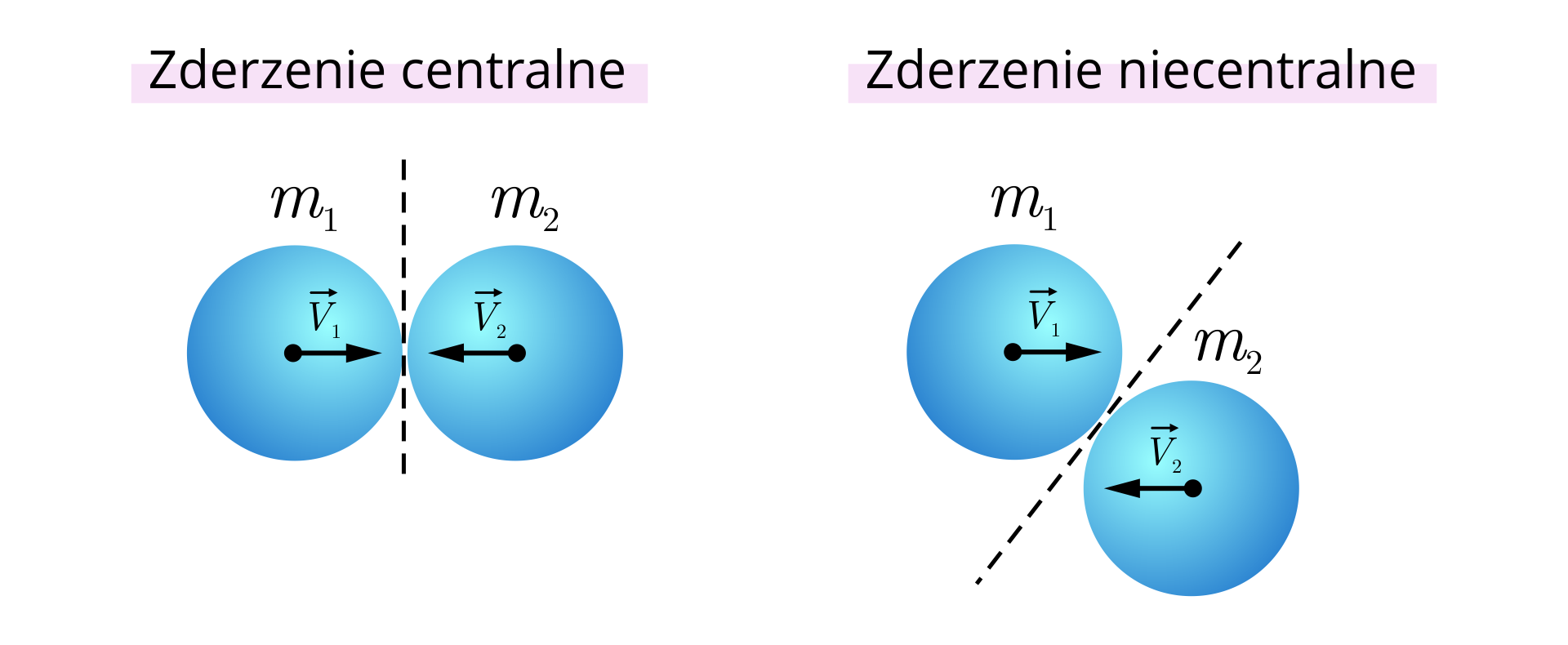
Zderzenie centralne to takie, w którym środki mas zderzających się ciał pozostają na prostej zarówno przed jak i po zderzeniu. Zderzenie niecentralne to takie, w wyniku którego przynajmniej jedno ciało zmienia kierunek swojego ruchu. Zderzenie niecentralne nazywane jest rykoszetem.

R1Anq6sgk9Ol1

Ilustracja składa się z dwóch części. W pierwszej części zderzenie centralne. Dwie kule o masach em jeden i em dwa, poruszające się z prędkościami odpowiednio fał jeden i fał dwa zderzają się. Ich środki mas znajdują się na tej samej prostej co wektory prędkości. Wektor fał jeden skierowany jest do środka kuli em dwa. Wektor fał dwa skierowany jest do środka kuli em jeden. W drugiej części zderzenie niecentralne. Dwie te same kule, z tymi samymi prędkościami, zderzają się. Ich środki i wektory prędkości tym razem nie leżą na tej samej prostej. — W zderzeniu centralnym środki mas i wektory prędkości zderzających się ciał znajdują się na jednej prostej, natomiast w zderzeniu niecentralnym tak nie jest
Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Na czym zatem polega sprężystość zderzeń? Sprężystość jest to właściwość ciał, która polega na przeciwstawianiu się efektowi odkształcenia czyli powracaniu do pierwotnego kształtu i rozmiaru po usunięciu działającej na ciało siły. Wiele materiałów posiada właściwości elastyczne np. guma, ale nawet takie jak stal, drewno czy kryształy. Sprężystość jest wprost proporcjonalna do siły, jaką ciało może wytrzymać bez uszkodzenia lub trwałej zmiany kształtu. Sprężystość może zależeć od wielu czynników jak temperatura (zwykle wzrost temperatury powoduje zmniejszenie sprężystości danego materiału) czy sama struktura lub zanieczyszczenia materiału. Elastyczność ciał można tez modyfikować przez odpowiednią obróbkę.

W zależności zatem od zderzających się ciał zderzenia mogą być sprężyste lub niesprężyste. Bez względu na rodzaj zderzenia spełniona jest zasada zachowania pęduzasada zachowania pęduzasada zachowania pędu dla układu ciał. Oznacza to, że pęd układu przed zderzeniem jest taki sam jak po zderzeniu. Dla przypomnienia pęd wyrażany jest jako iloczyn masy $m$ i prędkości $v$ ciała:

p = m \cdot v

Występuje wtedy zarówno zachowanie pędu jak i energii kinetycznej. Oznacza to, że nie występuje żadna siła, która powodowałaby zmianę energii. Zasada ta spełniona jest tylko dla zderzeń doskonale sprężystych. W tym przypadku nie ma strat energii kinetycznej. Zderzenia jakie znamy z otaczającego nas świata nie są doskonale sprężyste, następuje rozproszenie pewnych ilości energii.
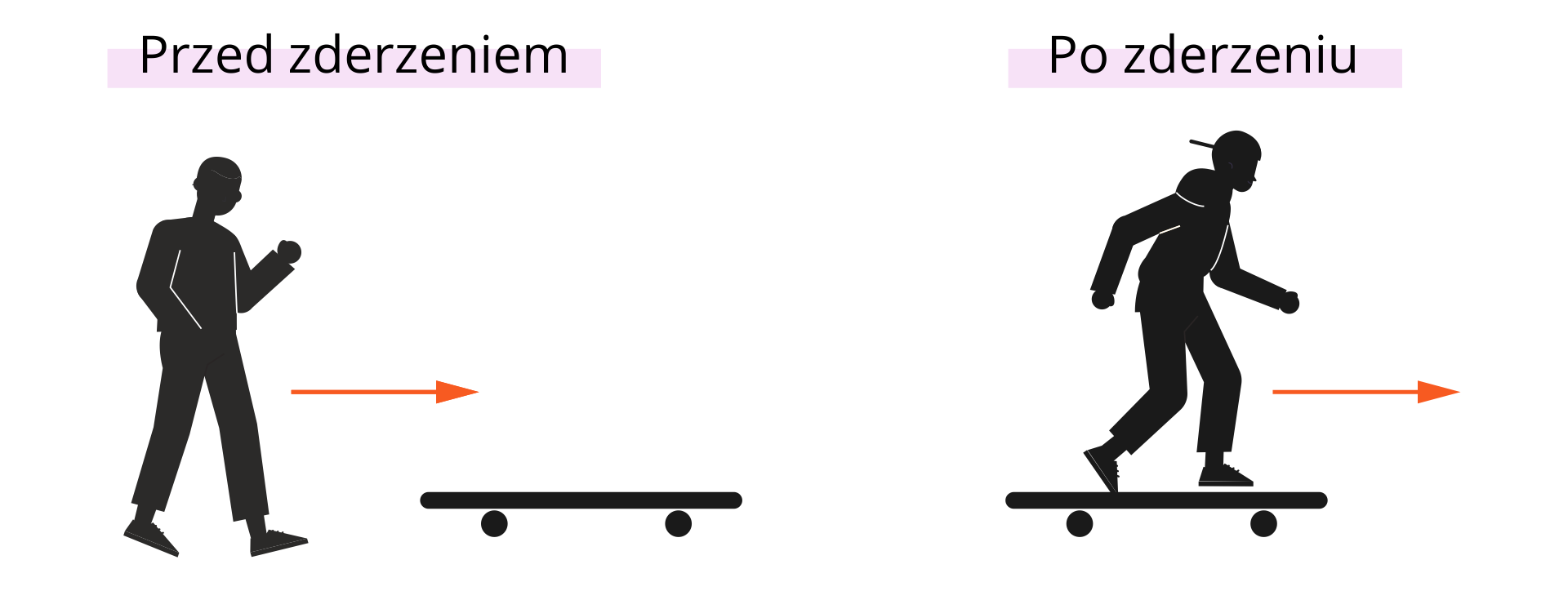
Zderzenie, w którym energia kinetyczna zmienia się w inny rodzaj energii podczas tego zderzenia lub rozprasza się, jest zderzeniem niesprężystym. Należy tutaj wyróżnić zderzenie doskonale niesprężyste, w którym ciała po zderzeniu łączą się i poruszają dalej razem.

Przykład 2

Oblicz prędkość jaką uzyska wózek sklepowy o masie $7 kg$ po wskoczeniu do niego chłopca o masie $50 kg$ , biegnącego z prędkością $4 \frac{m}{s}$ .

R1RgTa1x0UMYC

Ilustracja składa się z dwóch części. W pierwszej części sytuacja przed zderzeniem. Postać idzie w kierunku deski z kółkami. W drugiej części sytuacja po zderzeniu. Postać stoi na poruszającej się desce z kółkami. Deska porusza się w tym samym kierunku, w którym szła postać. — Ilustracja do przykładu 2. Przed zdarzeniem porusza się jedynie postać, po zdarzeniu deskorolka porusza się z postacią
Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Rozwiązanie:

Sytuację można rozpatrywać jako zderzenie chłopca z wózkiem. W tej sytuacji zadziała zasada zachowania pędu. Pęd przed zderzeniem posiadał tylko chłopiec, po zderzeniu pęd posiadają połączone masy chłopca i wózka, a zatem:

$m_{ch} \cdot v_{1} = (m_{ch} + m_{w}) \cdot v_{2}$

gdzie:
$m_{ch} = 50 kg$
$m_{w} = 7 kg$
$v_{1} = 4 \frac{m}{s}$
$v_{2}$ – to szukana prędkość wózka z chłopcem.

Po podstawieniu:

$50 kg \cdot 4 \frac{m}{s} = (50 kg + 7 kg) \cdot v_{2}$

$v_{2} = \frac{50 kg \cdot 4 \frac{m}{s}}{50 kg + 7 kg} = 3, 51 \frac{m}{s}$

Przykład 3

Udowodnij, że opisane poniżej zderzenie jest zderzeniem sprężystym.

Piłka o masie $4 kg$ porusza się z prędkością $1 \frac{m}{s}$ i zderza się z piłką o masie $2 kg$ poruszającą się z prędkością $2 \frac{m}{s}$ . Po zderzeniu prędkość pierwszej piłki wynosi $\frac{5}{3} \frac{m}{s}$ , a drugiej piłki $\frac{2}{3} \frac{m}{s}$ .

RzJBIwVyUQGdT

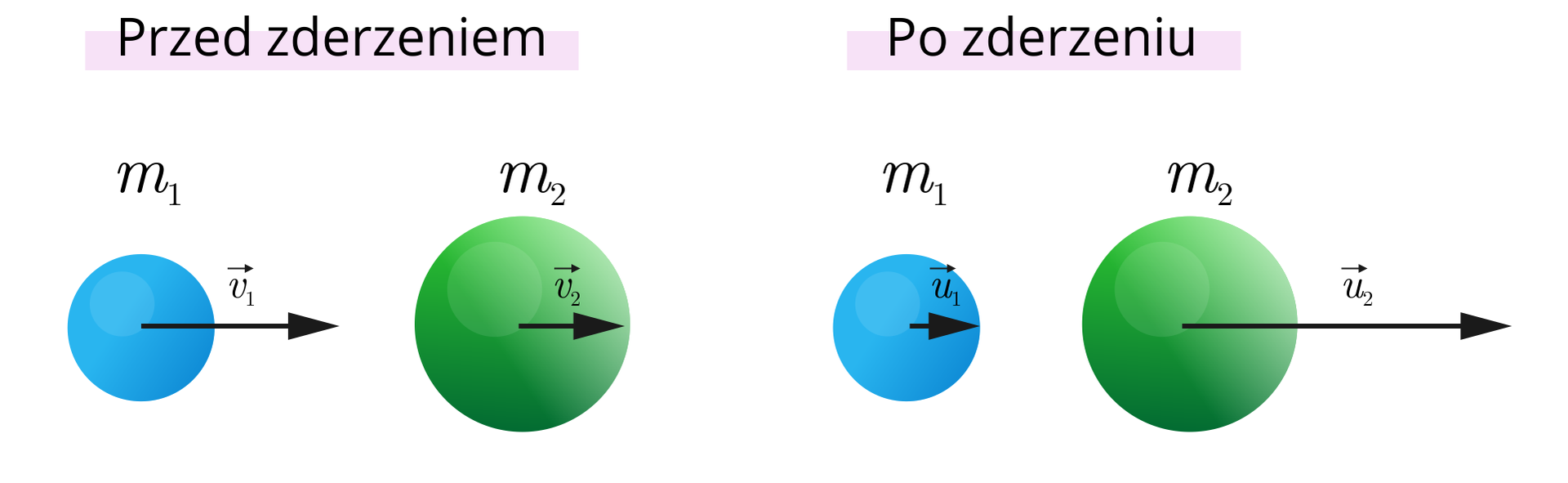
Ilustracja składa się z dwóch części. Na pierwszej części sytuacja przed zderzeniem. Dwie kule o masach em jeden i em dwa, poruszające się z prędkościami odpowiednio fał jeden i fał dwa, zderzają się. Ich środki mas znajdują się na tej samej prostej co wektory prędkości. Wektory prędkości fał jeden i fał dwa skierowane są w prawo. Wektor fał jeden jest dłuższy od wektora fał dwa. Na drugiej części sytuacja po zderzeniu. Dwie te same kule. Kula em jeden ma prędkość u jeden kula em dwa ma prędkość u dwa, a ich środki cały czas są na tej samej prostej. Wektory prędkości u jeden i u dwa skierowane są w prawo. Wektor u jeden jest krótszy od wektora u dwa. — Ilustracja do przykładu 3. Zarówno przed zderzeniem, jak i po nim, środki mas kulek i ich wektory prędkości znajdują się na jednej prostej
Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Rozwiązanie:

Zderzenie sprężyste to takie, w którym zachowana jest energia kinetyczna, a zatem:

$E_{K przed} = E_{K po}$

$E_{K przed} = \frac{m_{1} \cdot {v_{1}}^{2}}{2} + \frac{m_{2} \cdot {v_{2}}^{2}}{2}$

$E_{K po} = \frac{m_{1} \cdot {u_{1}}^{2}}{2} + \frac{m_{2} \cdot {u_{2}}^{2}}{2}$

gdzie:
$m_{1}$ – masa pierwszej piłki,
$m_{2}$ – masa drugiej piłki,
$v_{1}$ – prędkość pierwszej piłki przed zderzeniem,
$v_{2}$ – prędkość drugiej piłki przed zderzeniem
$u_{1}$ – prędkość pierwszej piłki po zderzeniu,
$u_{2}$ – prędkość drugiej piłki po zderzeniu.

Po podstawieniu:

$E_{K przed} = \frac{4 kg \cdot {(1 \frac{m}{s})}^{2}}{2} + \frac{2 kg \cdot {(2 \frac{m}{s})}^{2}}{2} = 2 J + 4 J = 6 J$ $E_{K po} = \frac{4 kg \cdot {(\frac{5}{3} \frac{m}{s})}^{2}}{2} + \frac{2 kg \cdot {(\frac{2}{3} \frac{m}{s})}^{2}}{2} = \frac{50}{9} J + \frac{4}{9} J = \frac{54}{9} J = 6 J$

Podsumowując, kiedy ciała przylegają do siebie po zderzeniu, to zderzenie jest doskonale niesprężyste. Jeśli ciała nie połączyły się, to rodzaj zderzenia możemy opisać, jeśli określimy czy początkowa energia kinetyczna jest taka sama jak końcowa. Jeśli jest taka sama, to zderzenie jest doskonale sprężyste. Jeśli energia kinetyczna zmieniła się, to zderzenie jest niesprężyste. Jeżeli nie ma udziału sił zewnętrznych, to pęd jest zachowany w tych przypadkach.

W otaczającym nas świecie możemy spotkać się z wieloma przykładami zderzeń. Począwszy od sprężystych zderzeń między atomami, zderzeń bil podczas gry w bilard, czy kozłowaniu piłki, po niesprężyste zderzenia pojazdów. Podczas zderzeń występują straty energii, ale często nie są one duże, a zderzenia takie można traktować jak doskonale sprężyste.

Wiedza na temat zderzeń wykorzystywana jest w wielu dziedzinach nauki, w tym także w balistyce, do analizy ruchu pocisku. Stosuje się często urządzenie zwane wahadłem balistycznym. Pocisk jest wystrzeliwany w zawieszony drewniany, nieruchomy blok. Pewne ilości energii kinetycznej zamieniane są w ciepło i dźwięk podczas wystrzału, a pozostała część jest wykorzystywana do deformacji drewnianego bloku. Jest to zderzenie niesprężyste, w którym pęd jest zachowany. Dzięki temu po zderzeniu blok odchyla się. Innym sposobem zastosowania zderzeń w balistyce jest badanie toru pocisku w specjalnym żelu balistycznym. Energia kinetyczna pocisku jest w tym przypadku wytracana po zderzeniu z żelem.

Rp8HkNQIeOlvS1

Zderzenie niesprężyste - ilustracja interaktywna

Źródło: GroMar Sp. z o. o., licencja: CC BY-SA 3.0.

Polecenie 1

Przyjmując, że masa kuli to $m$ , prędkość kuli to $v$ a masa klocka to $M$ , zapisz ile wynosi suma pędów oraz suma energii kinetycznych w sytuacji pierwszej.

R1GguMS9faFed

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

$p=mv$

$E_\mathrm{K}=\frac{mv^2}{2}$

Polecenie 2

Przyjmując, że masa kuli to $m$ a masa klocka to $M$ , zapisz co dzieje się z energią w sytuacji drugiej.

R6XTRvWeDUdFs

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Polecenie 3

Przyjmując, że masa kuli to $m$ , prędkość kuli i klocka to $u$ a masa klocka to $M$ , zapisz ile wynosi suma pędów oraz suma energii kinetycznych w sytuacji trzeciej. Załóż, że klocek lewituje (a nie wisi).

RUh5dIcJw2Xbp

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

$p=(m+M)u$

$E_\mathrm{K}=\frac{(m+M)u^2}{2}$

R1DBX28wFdukb

Na zdjęciu żel balistyczny podczas przelotu przez niego kuli. Żel ma formę dużego, przezroczystego prostopadłościanu. Na jego ścianie widać podłużne wybrzuszenie z pęknięciem na końcu, od którego odrywają się fragmenty substancji. — Pocisk przelatujący przez żel balistyczny wytraca energię
Źródło: dostępny w internecie: Wikipedia.org, licencja: CC BY-SA 3.0.

Wiedza o zderzeniach oraz zasada zachowania pędu i energii, znajduje swoje zastosowanie w analizie sportów. Oczywistym jest tutaj gra w bilard, która polega na zderzeniach kul i zmianach ich energii i prędkości. Możemy jednak pójść krok dalej i opisać w ten sposób nawet jazdę na deskorolce. Jazda zaczyna się od wejścia, wskoczenia na deskę, jest to więc rodzaj zderzenia niesprężystego, w wyniku którego dwa ciała zaczynają poruszać się razem. Podczas jazdy w skateparku [skejtpak] na tzw. halfpipe [hafpajp] (dwustronna rampa do wyskoków w kształcie litery U) następują dla odmiany ciągłe zmiany energii potencjalnej na kinetyczną i kinetycznej na potencjalną, dzięki czemu zawodnik może wyskoczyć ponad halfpipe i wykonać triki. Energia potencjalna zawodnika zależy od wysokości na jakiej się on znajduje - im jest wyżej, tym więcej ma energii potencjalnej. Zaczynając ruch na wysokości, zawodnik nie ma jeszcze energii kinetycznej, a dopiero zacznie ją zyskiwać jadąc w dół. Traci on wtedy energię potencjalną nabierając prędkości. Jego energia potencjalna zamienia się w energię kinetyczną. Po dotarciu do środka na dnie halfpipe’a, traci on całą energię potencjalną (przy założeniu, że znajduje się tam poziom zero), ale zyskuje dużo energii kinetycznej – posiada więc dużą prędkość. Dzięki temu zawodnik może wjechać na drugą stronę halfpipe’a i wyskoczyć w górę w celu wykonania trików. Podstawą jazdy jest zatem zasada zachowania energii – całkowita ilość energii kinetycznej i potencjalnej nie zmienia się, ale mogą być wzajemnie w siebie przekształcone. Oczywiście podczas jazdy na deskorolce zawodnik traci trochę energii na skutek tarcia kółek o podłoże. Z tego powodu jazda na deskorolce w górę i w dół halfpipe’a nie jest samoczynna i wymaga często dołożenia energii przez odepchnięcie się zawodnika.

Zasada zachowania energii czy energia zachowania pędu i zderzenia są powszechne i w mniejszej lub większej skali występują wokół nas.

Analiza ruchu

Poniższa symulacja służy do zobrazowania zderzeń centralnych sprężystych i niesprężystych. Po wyborze rodzaju zderzenia, stosunku mas kulek oraz stosunku ich prędkości zobaczysz, jak dobór tych parametrów wpływa na zachowanie kulek.

R1KwfB4caW8MB

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Symulacja. Do wyboru parametry: rodzaj zderzenia, masy ciał zderzających się oraz prędkości ciał zderzających się.
Można wybrać zderzenie sprężyste lub niesprężyste.
Masy ciał mogą być sobie równe, ciało pierwsze może być dwa razy lżejsze lub dwa razy cięższe.
Prędkości ciał mogą być sobie równe, ciało pierwsze może być dwa razy wolniejsze lub dwa razy szybsze.
Oznaczenia:

$m_{1}$ – masa ciała pierwszego,
$m_{2}$ – masa ciała drugiego,
$v_{1}$ – prędkość ciała pierwszego,
$v_{2}$ – prędkość ciała drugiego.

W poniższych tabelach zebrane są wyniki symulacji.

Zderzenie sprężyste	$m_1=m_2$	$m_1=0,5 m_2$	$m_1=2 m_2$
$v_1=v_2$	$v_{po}=v_{przed}$ $p_{po}=p_{przed}$ $E_{K po}=E_{K przed}$	$v_{1 po} \gt v_{2 po}$ $p_{po}=p_{przed}$ $E_{K po}=E_{K przed}$	$v_{1 po} \lt v_{2 po}$ $p_{po}=p_{przed}$ $E_{K po}=E_{K przed}$
$v_1=0,5 v_2$	$v_{1 po}=v_{2 przed}=2 v_{1 przed}$ $v_{2 po}=v_{1 przed}=0,5 v_{2 przed}$ $p_{po}=p_{przed}$ $E_{K po}=E_{K przed}$	$v_{1 po} \gt v_{2 po}$ $p_{po}=p_{przed}$ $E_{K po}=E_{K przed}$	$v_{1 po} = 0,5 v_{2 po}$ $p_{po}=p_{przed}$ $E_{K po}=E_{K przed}$
$v_1=2 v_2$	$v_{1 po}=v_{2 przed}=0,5 v_{1 przed}$ $v_{2 po}=v_{1 przed}=2 v_{2 przed}$ $p_{po}=p_{przed}$ $E_{K po}=E_{K przed}$	$v_{1 po} \gt 2 v_{2 po}$ $p_{po}=p_{przed}$ $E_{K po}=E_{K przed}$	$v_{1 po} \lt 2 v_{2 po}$ $p_{po}=p_{przed}$ $E_{K po}=E_{K przed}$

Zderzenie niesprężyste	$m_1=m_2$	$m_1=0,5 m_2$	$m_1=2 m_2$
$v_1=v_2$	$v_{po}=0$ $p_{po}=0$ $E_{K po}=0$	$v_{po} \lt v_{przed}$ $p_{po}=p_{przed}$ $E_{K po} \lt E_{K przed}$	$v_{po} \lt v_{przed}$ $p_{po}=p_{przed}$ $E_{K po} \lt E_{K przed}$
$v_1=0,5 v_2$	$v_{po}=0,5 v_{1 przed}=0,25 v_{2 przed}$ $p_{po}=p_{przed}$ $E_{K po} \lt E_{K przed}$	$v_{po} \lt v_{2 przed}$ $p_{po}=p_{przed}$ $E_{K po} \lt E_{K przed}$	$v_{po}=0$ $p_{po}=0$ $E_{K po}=0$
$v_1=2 v_2$	$v_{po}=0,5 v_{2 przed}=0,25 v_{1 przed}$ $p_{po}=p_{przed}$ $E_{K po} \lt E_{K przed}$	$v_{po}=0$ $p_{po}=0$ $E_{K po}=0$	$v_{po} \lt v_{1 przed}$ $p_{po}=p_{przed}$ $E_{K po} \lt E_{K przed}$

Polecenie 4

Jak zachowają się kulki w sytuacji, gdy ich masy i prędkości są identyczne, a zderzenie jest sprężyste, a jak gdy zderzenie tych samych kulek jest niesprężyste? Notatki możesz zapisać w polu poniżej.

R10JcOt9AN2tA

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Polecenie 5

Czy w zderzeniach sprężystych taka sama masa gwarantuje zawsze zachowanie prędkości kul po zderzeniu? Odpowiedz na pytanie. Notatki możesz zapisać w polu poniżej.

RouDooUfXYS8J

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Polecenie 6

Wyjaśnij, dlaczego w przypadku zderzenia niesprężystego, kiedy kule mają takie same masy i takie same prędkości przed zderzeniem, a po zderzeniu zatrzymują się, to pęd jest zachowany. Notatki możesz zapisać w polu poniżej.

RcK0ZQYG3iOt4

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Załóżmy, że każda kula ma masę $1 kg$ i porusza się z prędkością $1 \frac{m}{s}$ . Oznacza to, że pęd każdej z nich przed zderzeniem wynosi:

$p = 1 kg \cdot 1 \frac{m}{s} = 1 \frac{kg \cdot m}{s}$ .

Po zderzeniu kule zatrzymują się, czyli nie mają prędkości, więc pęd każdej z nich wynosi $0$ . Po zderzeniu taki jest też pęd całego układu. Pęd układu przed zderzeniem jednak też wynosi $0$ , mimo że każda z kul ma swój pęd. Dzieje się tak dlatego, że kule poruszają się naprzeciwko siebie, czyli zwroty wektorów pędu są przeciwne.

Analiza ruchu – ciąg dalszy

Poniższe wirtualne laboratorium służy do zobrazowania wpływu masy na ruch ciał. Zobaczysz, jak dobór tych parametrów wpływa na zachowanie ciał.

RaLWw85f0FafL

Wirtualne laboratorium. Przedstawione są dwie symulacje obrazujące wpływ masy na ruch ciał. W laboratorium można porównać energie ciał w ruchu w dwóch sytuacjach, dobierając parametry.

Symulacja pierwsza - Energia w skateparku.
Czy rzeczywiście posiadanie większej masy ułatwiałoby jazdę na deskorolce?
Można wybrać dwa warianty dwóch wielkości: masę zawodnika oraz wysokość rampy po której on jeździ. Masy do wyboru to 50 kilogramów lub 90 kilogramów. Wysokości ramp to 3 metry lub 5 metrów.
Po wyborze masy zawodnika i wysokości rampy wyświetla się animacja pokazująca ruch zawodnika na rampie oraz dwa wykresy: energii potencjalnej oraz energii kinetycznej. Zawodnik będąc na szczycie rampy posiada maksymalną energię potencjalną i zerową energię kinetyczną, natomiast na dnie rampy posiada zerową energię potencjalną i maksymalną energię kinetyczną. Zmieniając masę zawodnika i rozmiary rampy zmienia się wartość maksymalna tych energii w następujący sposób:
- dla zawodnika ważącego 50 kilogramów na rampie o wysokości 3 metry energia maksymalna wynosi 1500 dżuli,
- dla zawodnika ważącego 50 kilogramów na rampie o wysokości 5 metrów energia maksymalna wynosi 2500 dżuli,
- dla zawodnika ważącego 90 kilogramów na rampie o wysokości 3 metry energia maksymalna wynosi 2700 dżuli,
- dla zawodnika ważącego 90 kilogramów na rampie o wysokości 5 metrów energia maksymalna wynosi 4500 dżuli.
Odpowiedź na pytanie „czy rzeczywiście posiadanie większej masy ułatwiałoby jazdę na deskorolce?” brzmi więc następująco: Nie, doświadczenie przedstawia sytuację idealną bez oporów, zwiększenie masy to także zwiększenie tarcia.
Symulacja druga - Ruch pocisku.
Postaraj się przewidzieć, co mogłoby się stać, gdyby kula była stworzona z lodu.
Można wybrać dwa warianty dwóch wielkości: rodzaj strzelby oraz masę pocisku. Rodzaje strzelby do wyboru to nowoczesna, o dużej prędkości pocisku równej 400 metrów na sekundę, oraz starodawna, o małej prędkości pocisku równej 200 metrów na sekundę. Masy pocisku do wyboru to duża, czyli 100 gramów, oraz mała, czyli 10 gramów.
Po wyborze strzelby oraz masy pocisku wyświetla się animacja pokazująca strzelca strzelającego do tarczy strzelniczej. Wyświetla się również wartość energii kinetycznej pocisku oraz komentarz. Dla czterech możliwych wariantów warunków animacji są to:
- dla nowoczesnej strzelby o prędkości pocisku 400 metrów na sekundę i dużej masy pocisku równej 100 gramów energia kinetyczna wynosi 8000 dżuli, a komentarz brzmi następująco: strata energii kinetycznej, wzrost energii cieplnej, huk (dźwięk),
- dla nowoczesnej strzelby o prędkości pocisku 400 metrów na sekundę i małej masy pocisku równej 10 gramów energia kinetyczna wynosi 800 dżuli, a komentarz brzmi następująco: strata energii kinetycznej, wzrost energii cieplnej, huk (dźwięk),
- dla starodawnej strzelby o prędkości pocisku 200 metrów na sekundę i dużej masy pocisku równej 100 gramów energia kinetyczna wynosi 2000 dżuli, a komentarz brzmi następująco: strata energii kinetycznej, wzrost energii cieplnej, huk (dźwięk),
- dla starodawnej strzelby o prędkości pocisku 200 metrów na sekundę i małej masy pocisku równej 10 gramów energia kinetyczna wynosi 200 dżuli, a komentarz brzmi następująco: strata energii kinetycznej, wzrost energii cieplnej, huk (dźwięk).
Gdyby kula była stworzona z lodu, mogłaby się roztopić po uderzeniu w tarczę ze względu na kruchość materiału, ponadto lód mógłby się stopić, po zderzeniu wydziela się pewna ilość ciepła.

R113C8fzI9UUL

Polecenie 7

Zastanów się, czy rzeczywiście (jak to pokazano w pierwszej części powyższego multimedium) posiadanie większej masy ułatwiałoby jazdę na deskorolce. Notatki możesz zapisać w polu poniżej.

R9TQgPsPbTs4o

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Polecenie 8

W którym momencie jazdy na deskorolce po rampie największa jest energia kinetyczna, a w którym energia potencjalna? Notatki możesz zapisać w polu poniżej.

R1IKrSKTVPTfF

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Polecenie 9

Postaraj się przewidzieć, co mogłoby się stać, gdyby kula z drugiej części powyższego multimedium była stworzona z lodu. Notatki możesz zapisać w polu poniżej.

R14pN0CGoj38Z

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Sprawdź się

R5tqTyC8qvjJc

Ćwiczenie 1

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

R1u39d5ixAzBw

Ćwiczenie 2

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

R1CUIdMMSh3L8

Ćwiczenie 3

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

R16Yzq0VU6Vxk

Ćwiczenie 4

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

RvR32uv7wqx1Y

Ćwiczenie 5

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

R1TxCY1hCjjFy

Ćwiczenie 5

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Ćwiczenie 6

Określ, co stanie się z energią kinetyczną i pędem, gdy samochód o masie $900\,\mathrm{kg}$ zwiększy swoją prędkość od $10\,\mathrm{\frac{m}{s}}$ do $20\,\mathrm{\frac{m}{s}}$ .

R1IhSg95cQZ6o

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

$E_\mathrm{k1}=\frac{900\,\mathrm{kg}\cdot\left(10\,\mathrm{\frac{m}{s}}\right)^2}{2}=45000\,\mathrm{J}$

$E_\mathrm{k2}=\frac{900\,\mathrm{kg}\cdot\left(20\,\mathrm{\frac{m}{s}}\right)^2}{2}=180000\,\mathrm{J}$

$\frac{E_\mathrm{k2}}{E_\mathrm{k1}}=\frac{180000\,\mathrm{J}}{45000\,\mathrm{J}}=4$

$p_\mathrm{1}=900\,\mathrm{kg}\cdot10\,\mathrm{\frac{m}{s}}=9000\,\mathrm{\frac{kg\cdot m}{s}}$

$p_\mathrm{2}=900\,\mathrm{kg}\cdot20\,\mathrm{\frac{m}{s}}=18000\,\mathrm{\frac{kg\cdot m}{s}}$

$\frac{p_\mathrm{2}}{p_\mathrm{1}}=\frac{18000\,\mathrm{\frac{kg\cdot m}{s}}}{9000\,\mathrm{\frac{kg\cdot m}{s}}}=2$

Ćwiczenie 7

R1QEISDnnAson

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

$54 \frac{km}{h} = 15 \frac{m}{s}$

$500 g = 0, 5 kg$

$p=m\cdot v=0,5\,\mathrm{kg}\cdot15\,\mathrm{\frac{m}{s}}=7,5\,\mathrm{\frac{kg\cdot m}{s}}$

$E=\frac{m\cdot v^2}{2}=\frac{0,5\,\mathrm{kg}\cdot225\,\mathrm{\frac{m^2}{s^2}}}{2}=56,25\,\mathrm{J}$

Ćwiczenie 8

Ciało A o masie $2, 5 m$ poruszające się z prędkością $2 v$ zderza się centralnie z ciałem B o masie $1, 25 m$ , poruszającym się z prędkością $v$ w przeciwnym kierunku. W wyniku zderzenia ciało A zatrzymuje się, a ciało B zaczyna się poruszać w przeciwnym kierunku niż pierwotnie. Wiedząc, że zderzenie było doskonale sprężyste (zachowana jest energia kinetyczna), zapisz energię kinetyczną ciała B po zderzeniu.

R1YNx8cka4md3

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

$E_{kA} = \frac{2, 5 \cdot m \cdot {(2 v)}^{2}}{2} = \frac{10 \cdot m \cdot v^{2}}{2}$

$E_{kB} = \frac{1, 25 m \cdot v^{2}}{2}$

$E_{k} = \frac{10 \cdot m \cdot v^{2}}{2} + \frac{m \cdot v^{2}}{2} = \frac{11, 25 \cdot m \cdot v^{2}}{2}$

Energia kinetyczna ciała B po zderzeniu wynosi $\frac{11, 25 \cdot m \cdot v^{2}}{2}$ .

Słownik

zasada zachowania energii

zasada mówiąca o tym, że energia układu – na który nie działają siły spoza tego układu – przed zderzeniem jest taka sama, jak po zderzeniu.

zasada zachowania pędu

zasada mówiąca o tym, że pęd układu – na który nie działają siły spoza tego układu – przed zderzeniem jest taki sam, jak po zderzeniu; należy zwrócić uwagę na to, że pęd jest wielkością wektorową.

Bibliografia

Sagnowska B., Szot‑Gawlik D., Godlewska M., Rozenbajgier M., Rozenbajgier R., 2017, Świat fizyki, Warszawa, WSiP

bg‑gray2

Notatki

R1KG3WQpTKIDU

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.