Punkty kratowe należące do prostej

R1BwK0MPssQmi

Prostokątny układ współrzędnych możemy wykorzystać do opisu różnych obiektów oraz rozwiązywania problemów geometrycznych. Nazwa układu pochodzi od matematyka i filozofa Kartezjusza $(1596-1650)$ . W materiale dowiemy się, jak wyznaczać współrzędne różnych punktów, które należą do tej samej prostej, wyznaczonej przez dwa dowolne punkty. Dodatkowym warunkiem będzie to, aby ich obie współrzędne były liczbami całkowitymi.

Interaktywna treść merytorycznaInteraktywna treść merytoryczna
AnimacjaAnimacja
Zestaw ćwiczeń interaktywnychZestaw ćwiczeń interaktywnych
SłownikSłownik

Aby zrozumieć poruszane w tym materiale zagadnienia, przypomnij sobie:

Pojęcie kartezjańskiego układu współrzędnych.
Sposoby zaznaczania i odczytywania współrzędnych punktów zaznaczonych w prostokątnym układzie współrzędnych.

Twoje cele

Zdefiniujesz pojęcie punktu kratowego.
Wyznaczysz współrzędne punktów kratowych należących do zadanej prostej.
Określisz liczbę punktów kratowych, które spełniają zadane warunki.
Wykorzystasz zdobytą wiedzę do rozwiązywania problemów matematycznych.

Każdemu punktowi $P$ na płaszczyźnie możemy przyporządkować jednoznacznie parę liczb $(x, y)$ . Liczby te nazywamy współrzędnymi w prostokątnym układzie współrzędnychprostokątny układ współrzędnychprostokątnym układzie współrzędnych. Aby określić współrzędne punktu na płaszczyźnie znajdujemy rzuty prostopadłe punktu $P$ odpowiednio na osie $X$ i $Y$ i odczytujemy liczby $x$ i $y$ , które tym rzutom odpowiadają. Punkt $P$ o współrzędnych $x$ i $y$ zapisujemy $P = (x, y)$ . Poziomą oś $X$ nazywamy osią odciętych, a oś pionową $Y$ – osią rzędnych.

RACTJRUEwd7tc

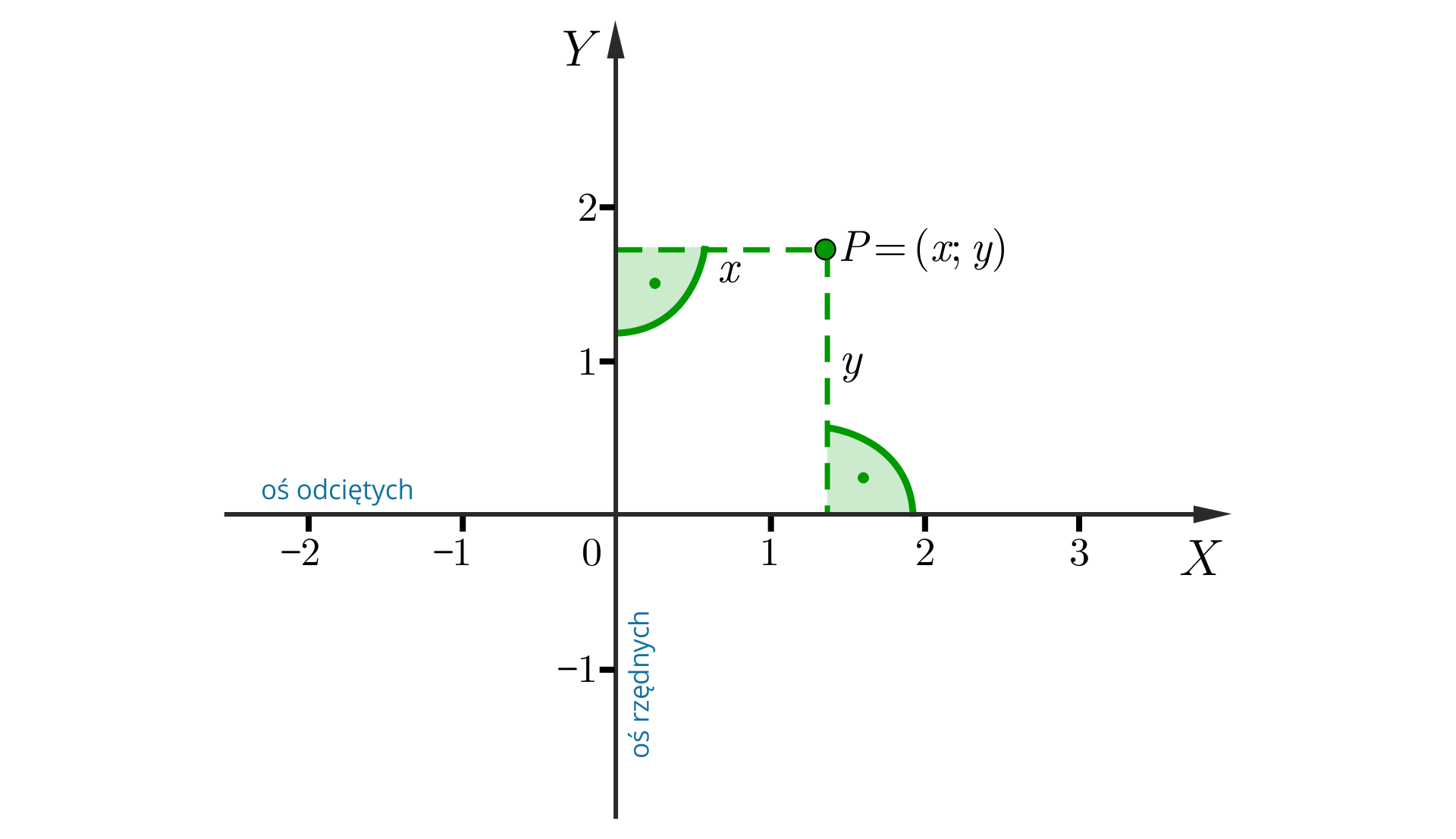
Grafika przedstawia kartezjański układ współrzędnych. Oś pozioma "X" ze zwrotem w prawą stronę ma podpis "oś odciętych", natomiast oś pionowa "Y" ze zwrotem w górę ma podpis "oś rzędnych". Na osi poziomej zaznaczone są wartości od -2 do 3, rosnące w prawą stronę o jedną jednostkę. Na osi pionowej zaznaczone są wartości od -1 do 2, rosnące w górę o jedną jednostkę. W pierwszej ćwiartce zaznaczony jest punkt "P" o współrzędnych dodatnich x, y. Punkt x znajduje się pomiędzy wartością 1 i 2 na osi poziomej, a punkt y znajduje się pomiędzy wartością 1 i 2 na osi pionowej. Od tych punktów poprowadzone są przerywane linie w kolorze zielonym. Między osiami oraz liniami do nich prostopadłymi, kolorem zielonym zaznaczone są kąty proste. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Każdemu punktowi $P$ na płaszczyźnie z układem współrzędnych odpowiada dokładnie jedna para liczb $(x, y)$ i odwrotnie, każdej parze liczb $(x, y)$ odpowiada w układzie współrzędnych dokładnie jeden punkt $P$ .

Zdefiniujmy pojęcie punktu kratowego.

punkt kratowy

Definicja: punkt kratowy

Punkt w prostokątnym układzie współrzędnych, którego obie współrzędne są liczbami całkowitymi nazywamy punktem kratowym.

Wiadomo, że przez każde dwa punkty przechodzi dokładnie jedna prosta.

Zaznaczmy w prostokątnym układzie współrzędnych punkty $A$ i $B$ o współrzędnych odpowiednio: $A = (- 4, 3)$ oraz $B = (- 1, 1)$ .

RQGr8dkAsqw5K

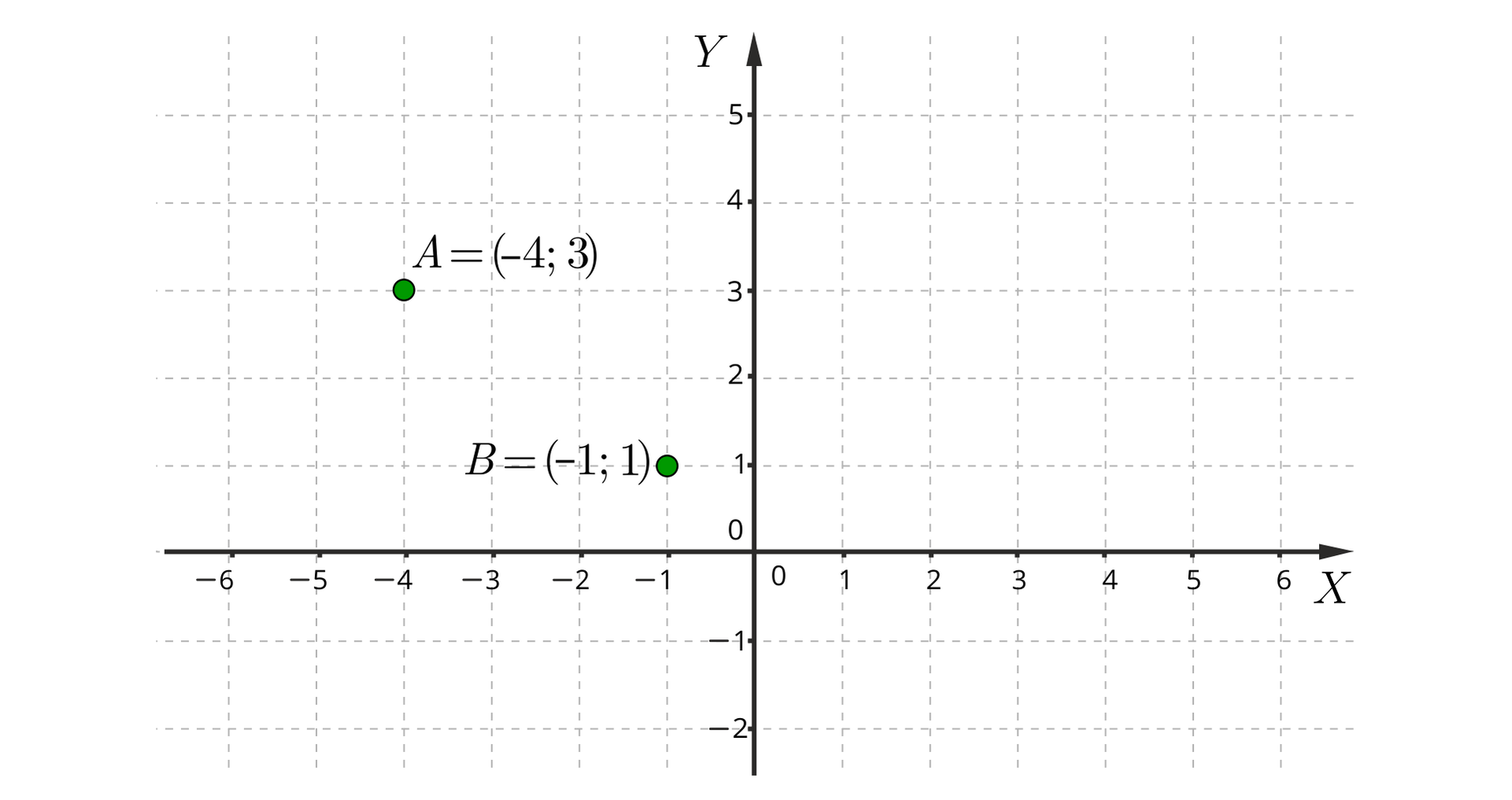
Grafika przedstawia kartezjański układ współrzędnych. Oś pozioma "X" ma zwrot w prawą stronę, natomiast oś pionowa "Y" ma zwrot w górę. Na osi poziomej zaznaczone są wartości od -6 do 6, rosnące w prawą stronę o jedną jednostkę. Na osi pionowej zaznaczone są wartości od -2 do 5, rosnące w górę o jedną jednostkę. W drugiej ćwiartce zaznaczony jest punkt "A" o współrzędnych -4, 3 oraz punkt "B" o współrzędnych -1, 1. Punkty zaznaczone są kółeczkami w kolorze zielonym. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

W celu wyznaczenia innych punktów, które należą do prostej wyznaczonej przez punkty $A$ i $B$ stosujemy następującą procedurę:

Obliczamy różnice pierwszych współrzędnych i drugich współrzędnych obu punktów:

$- 1 - (- 4) = 3$

$1 - 3 = - 2$

Przesuwając się zgodnie z kierunkiem osi $X$ kolejne punkty kratowe to punkty o współrzędnych:

$(- 1 + 3, 1 - 2) = (2, - 1)$

$(2 + 3, - 1 - 2) = (5, - 3)$

Przesuwając się przeciwnie do kierunku osi $X$ kolejne punkty kratowe to punkty o współrzędnych:

$(- 4 - 3, 3 + 2) = (- 7, 5)$

$(- 7 - 3, 5 + 2) = (- 10, 7)$

RYjnAQ9HvDe48

Ważne!

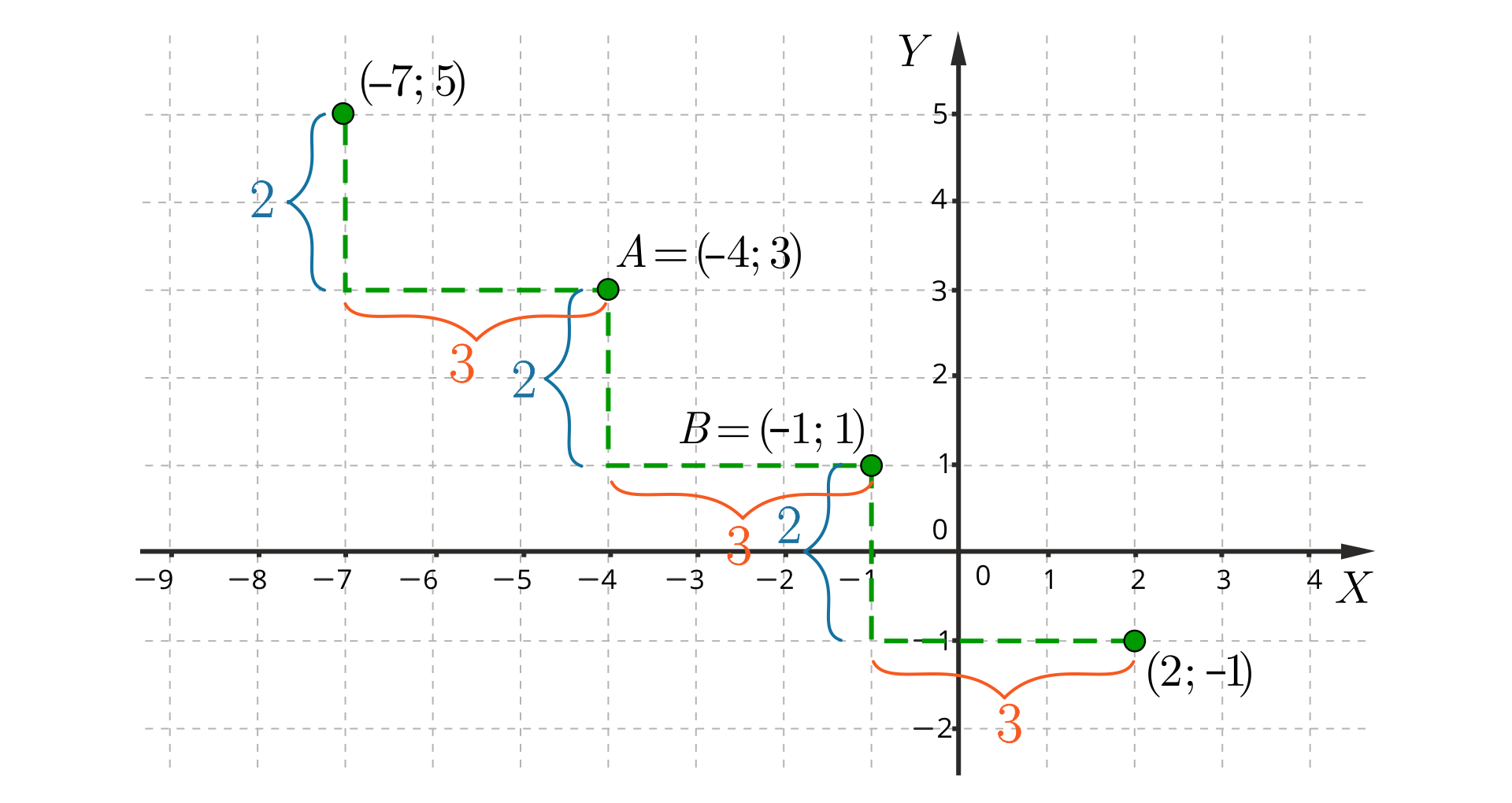
Punkty nazywamy współliniowymi wtedy i tylko wtedy, gdy leżą na jednej prostej.

Przykład 1

Wyznaczymy współrzędne dwóch różnych punktów, które należą do prostej $A B$ wyznaczonej przez punkty o współrzędnych: $A = (2, - 1)$ oraz $B = (1, - 3)$ .

Rozwiązanie:

Obliczamy różnice pierwszych współrzędnych i drugich współrzędnych obu punktów:
$1 - 2 = - 1$
$- 3 - (- 1) = - 2$
Obliczamy współrzędne innych punktów kratowych należących do prostej $A B$ :
$(1 - 1, - 3 - 2) = (0, - 5)$
$(0 - 1, - 5 - 2) = (- 1, - 7)$

Zauważmy, że do prostej wyznaczonej przez punkty o współrzędnych $A = (x, 0)$ oraz $B = (0, y)$ , gdzie $x$ i $y$ są liczbami całkowitymi, należą punkty kratowe o współrzędnych $(2 x, - y)$ oraz $(- x, 2 y)$ .

Przykład 2

Podamy współrzędne dwóch punktów kratowych, które należą do prostej wyznaczonej przez punkty o współrzędnych $(4, - 1)$ oraz $(- 2, 2)$ .

Rozwiązanie:

Zauważmy, że wobec powyższego faktu do prostej wyznaczonej przez punkty o współrzędnych $(4, - 1)$ oraz $(- 2, 2)$ należą punkty kratowe o współrzędnych $(2, 0)$ i $(0, 1)$ .

Przykład 3

W prostokątnym układzie współrzędnych zaznaczono punkty $A$ i $B$ , jak na poniższym rysunku. Wyznaczymy współrzędne wszystkich punktów kratowych, które należą do prostej wyznaczonej przez punkty $A$ i $B$ , jeżeli te współrzędne są liczbami dodatnimi.

R1Dkm9ige4Cui

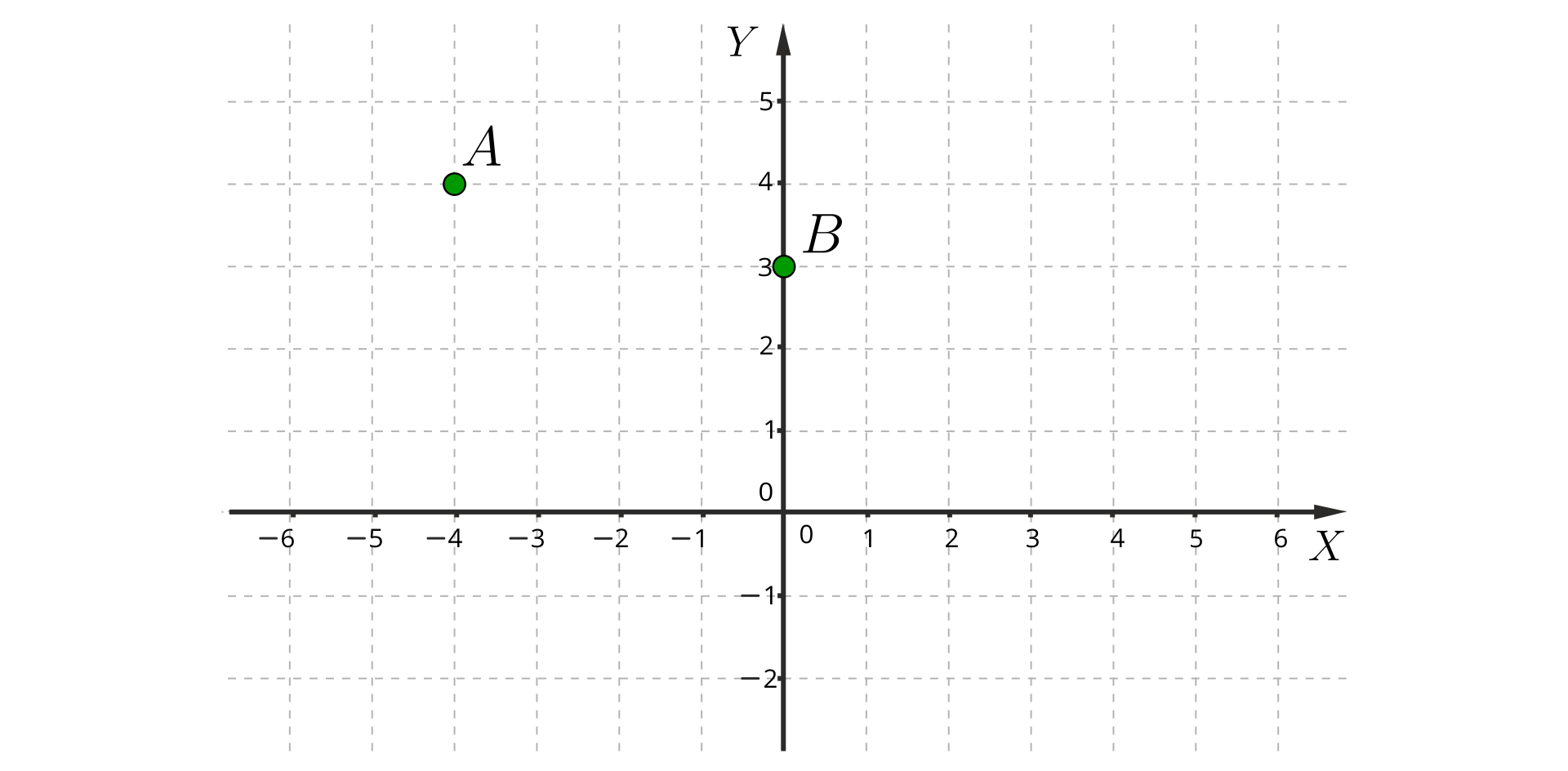
Rozwiązanie:

Odczytujemy współrzędne punktów $A$ i $B$ : $A = (- 4, 4)$ i $B = (0, 3)$ .
Obliczamy różnice pierwszych współrzędnych i drugich współrzędnych obu punktów:
$0 - (- 4) = 4$
$3 - 4 = - 1$
Wyznaczamy współrzędne punktów kratowych, które należą do prostej $A B$ :
$(0 + 4, 3 - 1) = (4, 2)$
$(4 + 4, 2 - 1) = (8, 1)$
$(8 + 1, 1 - 1) = (12, 0)$
Zatem istnieją tylko dwa punkty kratowe o obu współrzędnych dodatnich, które należą do prostej $A B$ : $(4, 2)$ , $(8, 1)$ .

Przykład 4

Dane są punkty o współrzędnych $A = (2 m + 3, - 1)$ , $B = (4, 1)$ , $C = (5, 3)$ . Wyznaczymy wartość $m$ , jeżeli wiadomo, że punkty $A$ , $B$ , $C$ są punktami kratowymi należącymi do tej samej prostej.

Rozwiązanie:

Obliczamy różnice pierwszych współrzędnych i drugich współrzędnych punktów $B$ i $C$ :
$5 - 4 = 1$ ,
$3 - 1 = 2$ .
Dostajemy zatem, że punkty, które leżą na tej samej prostej, co punkty $B$ i $C$ otrzymujemy następująco:

dodając lub odejmując od pierwszej współrzędnej jednego z punktów wielokrotności liczby $1$ oraz,
dodając lub odejmując od drugiej współrzędnej jednego z punktów wielokrotności liczby $2$ .

Zauważmy, że różnica drugich współrzędnych punktów $A$ i $B$ wynosi $1 - (- 1) = 2$ . Stąd, aby obliczyć wartość $m$ rozwiązujemy równanie.
$4 - 1 = 2 m + 3$
$3 = 2 m + 3$
$2 m = 0$
$m = 0$
Wobec tego wartość $m$ wynosi $0$ .

Punkty kratowe możemy wykorzystać do rozwiązywania problemów matematycznych.

Przykład 5

Wyznaczymy współrzędne punktu przecięcia prostych $A B$ i $C D$ , do których należą punkty o współrzędnych $A = (- 6, 0)$ i $B = (- 3, 3)$ oraz $C = (0, 2)$ i $D = (3, 1)$ .

Rozwiązanie:

Wyznaczymy współrzędne punktów kratowych, które należą do prostej $A B$ . W tym celu:

obliczamy różnice pierwszych współrzędnych i drugich współrzędnych obu punktów:
$- 3 - (- 6) = 3$
$3 - 0 = 3$
wyznaczamy współrzędne innych punktów kratowych leżących na prostej $A B$ :
$(- 3 + 3, 3 + 3) = (0, 6)$
$(- 6 - 3, 0 - 3) = (- 9, - 3)$

Wyznaczymy współrzędne punktów kratowych, które należą do prostej $C D$ . W tym celu:

obliczamy różnice pierwszych współrzędnych i drugich współrzędnych obu punktów:
$3 - 0 = 3$
$1 - 2 = - 1$
wyznaczamy współrzędne innych punktów kratowych leżących na prostej $C D$ :
$(3 + 3, 1 - 1) = (6, 0)$
$(0 - 3, 2 + 1) = (- 3, 3)$

Zauważmy, że punkt o współrzędnych $(- 3, 3)$ należy do prostej $A B$ i prostej $C D$ .
Zatem punkt o współrzędnych $(- 3, 3)$ jest punktem wspólnym tych prostych.

Oczywiście proste na płaszczyźnie mogą się przecinać w punkcie, który nie jest punktem kratowym.

Notatnik

R19ExGTN2MbJz

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Animacja

Obejrzyj animację dotyczącą wyznaczania punktów kratowych, które należą do tej samej prostej.

R21z2uT6k6tYJ1

Punkty kratowe należące do prostej.
Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Polecenie 1

Przeanalizuj jeszcze raz zadania omówione w animacji i spróbuj znaleźć jeszcze inne sposoby ich rozwiązania.

RJBszBGuiEEvh

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Polecenie 2

Sprawdź, czy punkty o współrzędnych $A = (- 4, - 1)$ , $B = (- 2, - 2)$ oraz $C = (6, - 6)$ są punktami kratowymi, które są współliniowe.

RJBszBGuiEEvh

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

$I$ sposób:
Obliczamy różnice pierwszych i drugich współrzędnych punktów $A$ i $B$ :
$- 2 - (- 4) = 2$
$- 2 - (- 1) = - 1$
Obliczamy współrzędne innych punktów kratowych należących do prostej $A B$ :
$(- 2 + 2, - 2 - 1) = (0, - 3)$
$(0 + 2, - 3 - 1) = (2, - 4)$
$(2 + 2, - 4 - 1) = (4, - 5)$
$(4 + 2, - 5 - 1) = (6, - 6)$
Zauważmy, że otrzymaliśmy współrzędne punktu $C$ , zatem punkty o współrzędnych $A = (- 4, - 1)$ , $B = (- 2, - 2)$ , $C = (6, - 6)$ leżą na jednej prostej, czyli są współliniowe.
$II$ sposób:
Podstawiamy współrzędne punktów $A$ , $B$ , $C$ do następującej zależności:
$\frac{y_{B} - y_{A}}{x_{B} - x_{A}} = \frac{y_{C} - y_{B}}{x_{C} - x_{B}}$
Zatem
$\frac{- 2 - (- 1)}{- 2 - (- 4)} = \frac{- 6 - (- 2)}{6 - (- 2)}$
Po uproszczeniu otrzymujemy, że $\frac{- 1}{2} = \frac{- 4}{8}$ . Ponieważ równość jest prawdziwa, zatem punkty $A$ , $B$ , $C$ są punktami kratowymi współliniowymi.

Polecenie 3

Oblicz, dla jakich wartości m, punkty o współrzędnych $A = (- 2, 2)$ , $B = (0, 3)$ , $C = (2, m)$ są kolejnymi punktami kratowymi współliniowymi.

RJBszBGuiEEvh

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Wykorzystaj zależność $\frac{y_{B} - y_{A}}{x_{B} - x_{A}} = \frac{y_{C} - y_{B}}{x_{C} - x_{B}}$ .

Ponieważ punkty $A, B, C$ są kolejnymi punktami kratowymi, to zachodzi równość:

$\frac{y_{B} - y_{A}}{x_{B} - x_{A}} = \frac{y_{C} - y_{B}}{x_{C} - x_{B}}$

Podstawiamy współrzędne punktów $A, B, C$ do powyższej równości:

$\frac{3 - 2}{0 - (- 2)} = \frac{m - 3}{2 - 0}$

Po wykonaniu obliczeń otrzymujemy równanie:

$\frac{1}{2} = \frac{m - 3}{2}$

Zatem $1 = m - 3$ , więc $m = 4$ .

Odpowiedź: Szukana wartość $m$ wynosi $4$ .

Polecenie 4

Punkty $A = (0, - 2)$ , $B = (4, - 2)$ , $C = (m - 7, m)$ leżą na jednej prostej. Wyznacz współrzędne punktu $C$ .

Re34lz5l3GUOz

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Zauważ, że punkty $A$ , $B$ , $C$ leżą na prostej równoległej do osi $X$ .

Punkty $A$ , $B$ , $C$ leżą na prostej równoległej do osi $X$ , zatem $m = - 2$ .

$- 2 - 7 = - 9$

Odpowiedź: $C = (- 9, - 2)$ .

Zestaw ćwiczeń interaktywnych

Pokaż ćwiczenia:

RCBOMPVZMjPsg

Ćwiczenie 1

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

RvrBZO8RgAnog

Ćwiczenie 2

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

RhipCjySgjBjO

Ćwiczenie 3

Przeciągnij i upuść lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej, aby uzupełnić zdania. Punkt kratowy, to taki punkt, którego obie współrzędne są liczbami 1. nieparzystymi, 2.

8

, 3.

6

, 4.

7

, 5. wymiernymi, 6. całkowitymi, 7.

4

, 8. parzystymi, 9.

2

, 10.

3

, 11.

9

, 12.

5

. Pomiędzy punktami o współrzędnych

(- 2, 4)

oraz

(3, - 1)

leżą dokładnie 1. nieparzystymi, 2.

8

, 3.

6

, 4.

7

, 5. wymiernymi, 6. całkowitymi, 7.

4

, 8. parzystymi, 9.

2

, 10.

3

, 11.

9

, 12.

5

punkty kratowe, które leżą na prostej wyznaczonej przez te punkty.
Pomiędzy punktami o współrzędnych

(- 3, - 6)

oraz

(3, 0)

leży dokładnie 1. nieparzystymi, 2.

8

, 3.

6

, 4.

7

, 5. wymiernymi, 6. całkowitymi, 7.

4

, 8. parzystymi, 9.

2

, 10.

3

, 11.

9

, 12.

5

punktów kratowych, które leżą na prostej wyznaczonej przez te punkty.

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

R1NOuRp0PH7x2

Ćwiczenie 4

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

RxeE3trWuHhGG1

Ćwiczenie 5

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

RI4MEGjjERYmq

Ćwiczenie 5

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

R15Wn17L2mkT6

Ćwiczenie 6

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ćwiczenie 7

Wyznacz współrzędne punktu przecięcia prostych $A B$ i $C D$ , do których należą punkty o współrzędnych $A = (- 1, 4)$ i $B = (0, 3)$ oraz $C = (0, - 3)$ i $D = (1, - 1)$ .

RJBszBGuiEEvh

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Wyznacz kilka punktów kratowych, które należą do prostej $A B$ i do prostej $C D$ .

Wyznaczymy współrzędne punktów kratowych, które należą do prostej $A B$ . W tym celu:

obliczamy różnice pierwszych współrzędnych i drugich współrzędnych obu punktów:
$0 - (- 1) = 1$ ,
$3 - 4 = - 1$ ,
wyznaczamy współrzędne innych punktów kratowych leżących na prostej $A B$ :
$(0 + 1, 3 - 1) = (1, 2)$ ,
$(1 + 1, 2 - 1) = (2, 1)$ .

Wyznaczymy współrzędne punktów kratowych, które należą do prostej $C D$ . W tym celu:

obliczamy różnice pierwszych współrzędnych i drugich współrzędnych obu punktów:
$1 - 0 = 1$ ,
$- 1 - (- 3) = 2$ ,
wyznaczamy współrzędne innych punktów kratowych leżących na prostej $C D$ :
$(1 + 1, - 1 + 2) = (2, 1)$ ,
$(2 + 1, 1 + 2) = (3, 3)$ .

Zauważmy, że punkt o współrzędnych $(2, 1)$ należy do prostej $A B$ i prostej $C D$ .
Zatem punkt o współrzędnych $(2, 1)$ jest punktem przecięcia tych prostych.

Ćwiczenie 8

Wyznacz, dla jakiej wartości $m$ punkty $A$ , $B$ , $C$ o współrzędnych $A = (- 5, - 3)$ , $B = (0, - 1)$ oraz $C = (2 m - 3, 1)$ są punktami kratowymi, które leżą na jednej prostej.

RJBszBGuiEEvh

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Oblicz najpierw różnicę pierwszych i drugich współrzędnych punktów $A$ i $B$ , a nastepnie wyznacz współrzędne kolejnego punktu kratowego, który należy do prostej $A B$ .

Obliczamy różnice pierwszych współrzędnych i drugich współrzędnych obu punktów:
$0 - (- 5) = 5$ ,
$- 1 - (- 3) = 2$ .

Wyznaczymy współrzędne kolejnego punkt kratowego, należącego do prostej $A B$ :
$(0 + 5, - 1 + 2) = (5, 1)$ .

Zauważmy, że otrzymany punkt ma taką samą drugą współrzędną jak punkt $C$ . Ponieważ punkty $A$ , $B$ , $C$ są punktami kratowymi należącymi do tej samej prostej, zatem do wyznaczenia wartości $m$ rozwiązujemy równanie:

$2 m - 3 = 5$
$2 m = 8$
$m = 4$ .

Wobec tego wartość $m$ wynosi $4$ .

Słownik

prostokątny układ współrzędnych

para osi liczbowych prostopadłych do siebie, o wspólnym początku, nazywanym początkiem układu współrzędnych

Bibliografia

Babiański W., Braun M., Janowicz J., Mańkowska A., Paszyńska M., Szmytkiewicz E., Wej K., (2020), Matematyka z kluczem $7$ , Warszawa: Wydawnictwo Nowa Era.

Dąbrowski M., (2020), Matematyczne eksperymenty. Geometria nie tylko dla klas $1 - 3$ , Opole: Wydawnictwo Nowik.

Dobrowolska M. (red.), (2018), Matematyka z plusem, Gdańsk: Gdańskie Wydawnictwo Oświatowe.