Równanie prostej w postaci ogólnej oraz w postaci kierunkowej
Wiesz już, że:
prosta prostopadła do osi nie jest wykresem żadnej funkcji.
jeżeli na wykresie funkcji liniowej leżą dwa różne punkty i , (gdzie ), to współczynnik kierunkowy prostej, będącej wykresem funkcji, jest równy
natomiast wyraz wolny jest równy
każda prosta, będąca wykresem funkcji liniowej, która przechodzi przez punkt , ma równanie , co zapisujemy w postaci
każda prosta, będąca wykresem funkcji liniowej, która przechodzi przez dwa różne punkty i , ma równanie
Uruchom aplet i wykonaj podane polecenia.
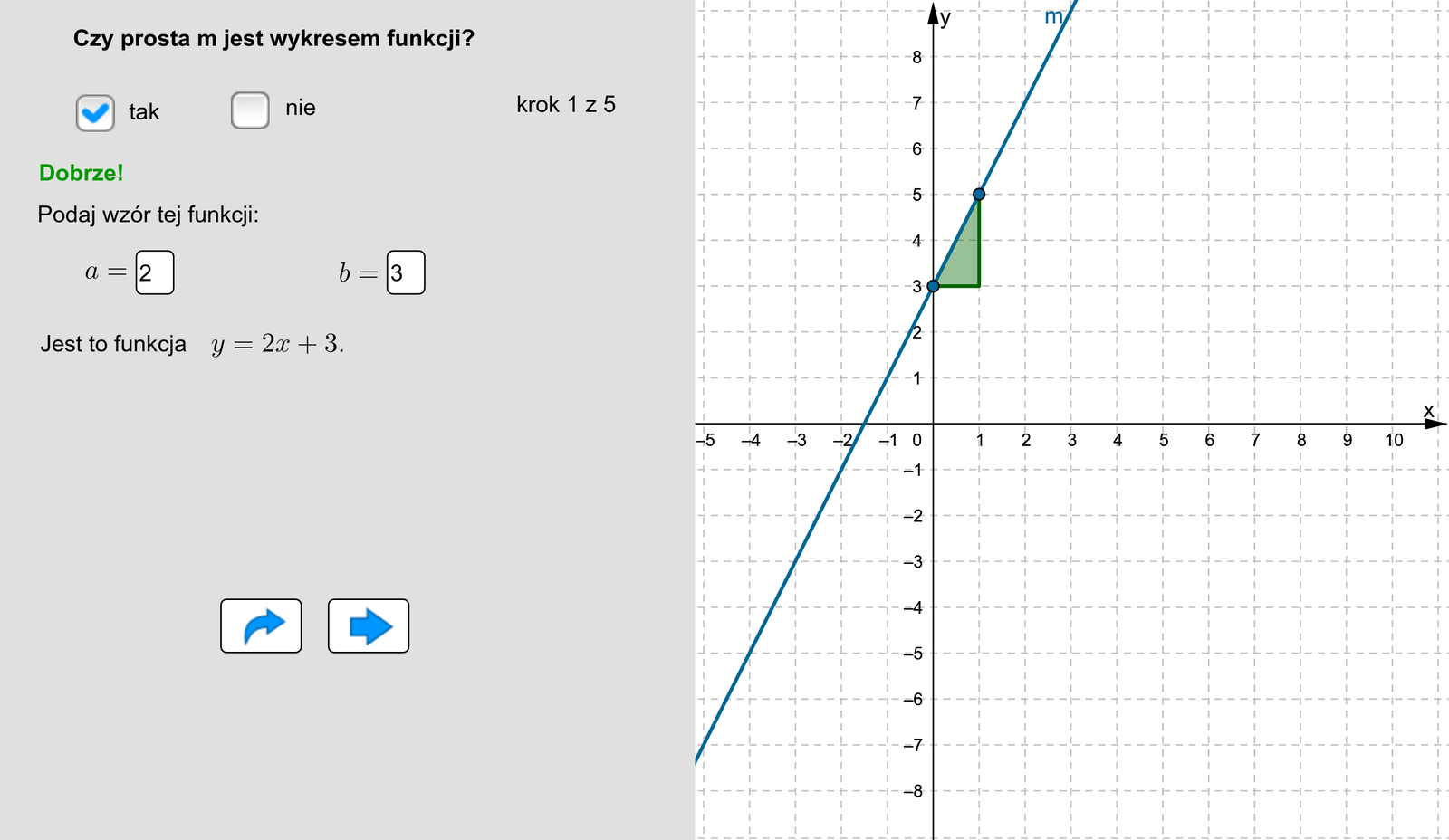
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PPi1IUFXl
Dopasuj do każdego rysunku odpowiednie równanie prostej.
RExbpLpyHdFdb1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.RL5diwP2EhA091 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.R1FBqXhPJBjGj1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.RdpGBwyyMYPXp1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.RglJqpdF8Hqpu1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.RIeLZ6PR3ZvdP1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Połącz w pary postać ogólną prostej z jej postacią kierunkową.
<span aria-label="y, równa się, początek ułamka, jeden, mianownik, siedem, koniec ułamka, x, plus, początek ułamka, pięć, mianownik, siedem, koniec ułamka" role="math"><math><mi>y</mi><mo>=</mo><mfrac><mn>1</mn><mn>7</mn></mfrac><mi>x</mi><mo>+</mo><mfrac><mn>5</mn><mn>7</mn></mfrac></math></span>, <span aria-label="y, równa się, pięć x, minus, początek ułamka, jeden, mianownik, trzy, koniec ułamka" role="math"><math><mi>y</mi><mo>=</mo><mn>5</mn><mi>x</mi><mo>-</mo><mfrac><mn>1</mn><mn>3</mn></mfrac></math></span>, <span aria-label="y, równa się, trzy x, plus, jeden" role="math"><math><mi>y</mi><mo>=</mo><mn>3</mn><mi>x</mi><mo>+</mo><mn>1</mn></math></span>, <span aria-label="x, plus, y, plus, trzy, równa się, zero" role="math"><math><mi>x</mi><mo>+</mo><mi>y</mi><mo>+</mo><mn>3</mn><mo>=</mo><mn>0</mn></math></span>, <span aria-label="y, równa się, początek ułamka, jeden, mianownik, trzy, koniec ułamka, x, minus, początek ułamka, trzy, mianownik, cztery, koniec ułamka" role="math"><math><mi>y</mi><mo>=</mo><mfrac><mn>1</mn><mn>3</mn></mfrac><mi>x</mi><mo>-</mo><mfrac><mn>3</mn><mn>4</mn></mfrac></math></span>
Wyznaczymy równanie prostej, przechodzącej przez punkty i .
Współczynnik kierunkowy tej prostej jest równy
Równanie prostej możemy zapisać w postaci
Współczynnik obliczymy, wstawiając do równania współrzędne dowolnego punktu należącego do tej prostej, np.
więc . Wynika z tego, że równanie prostej, przechodzącej przez punkty
i , ma postać:

Zauważmy, że mnożąc obie strony równania prostej przez , otrzymamy inną postać tego równania:
Po uporządkowaniu możemy zapisać
Jest to równanie tej samej prostej, przechodzącej przez punkty i , zapisane w postaci ogólnej.
Równanie , gdzie , i są liczbami rzeczywistymi oraz i nie są jednocześnie równe zero, nazywamy równaniem ogólnym prostej.

Film dostępny pod adresem /preview/resource/ROGdrUlYNxzO3
Animacja przedstawia jak przekształcić równanie prostej w postaci kierunkowej w równanie prostej w postaci ogólnej oraz odwrotnie.
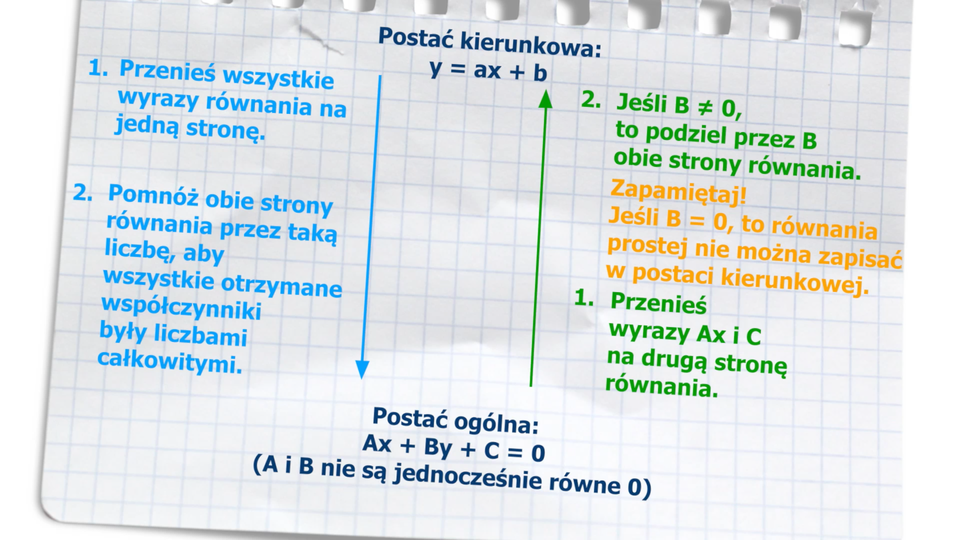
Film dostępny pod adresem /preview/resource/R1AeBeD3ifDSu
Animacja przedstawia schemat postępowania, który ułatwia zamianę postaci równania prostej z kierunkowej na ogólną i odwrotnie.
Wyznaczymy równanie ogólne prostej, przechodzącej przez punkty i , gdzie . Zauważmy, że korzystając ze wzoru
otrzymamy postać kierunkową prostej.
Możemy jednak przekształcić wzór tak, aby można było otrzymać również postać ogólną prostej.
Od obu stron równania odejmiemy wyrażenie
Mnożymy obie strony przez
Zauważmy, że jeżeli , to otrzymany wzór opisuje prostą równoległą do osi , przechodzącą przez punkty i . Ponieważ i , to . Wówczas mamy
Równanie prostej, przechodzącej przez dwa punkty i , ma postać
Wyznaczymy równanie prostej, przechodzącej przez punkty i .
Po podstawieniu współrzędnych punktów i do wzoru
otrzymamy
Po uporządkowaniu

Wyznaczymy równanie prostej, przechodzącej przez punkty i .
Po podstawieniu współrzędnych punktów i do wzoru
otrzymamy
Po uporządkowaniu otrzymaliśmy równanie prostej w postaci ogólnej

Jest to prosta prostopadła do osi . Tej prostej nie można opisać równaniem w postaci kierunkowej, ponieważ nie jest ona wykresem funkcji liniowej.
Uwaga
Równanie tej prostej wyznaczymy szybciej, jeśli zauważymy, że pierwsze współrzędne obu punktów są jednakowe i równe , a drugie są różne. Oznacza to, że równanie prostej, przechodzącej przez te punkty, ma postać , czyli .
Połącz w pary proste z punktami przez nie przechodzącymi.
<span aria-label="A, równa się, nawias, minus, dwa kropka dwa zamknięcie nawiasu, przecinek, B, równa się, nawias jeden kropka trzy zamknięcie nawiasu" role="math"><math><mi>A</mi><mo>=</mo><mo>(</mo><mo>-</mo><mn>2</mn><mo>,</mo><mn>2</mn><mo>)</mo><mo>,</mo><mi>B</mi><mo>=</mo><mo>(</mo><mn>1</mn><mo>,</mo><mn>3</mn><mo>)</mo></math></span>, <span aria-label="A, równa się, nawias dwa kropka trzy zamknięcie nawiasu, przecinek, B, równa się, nawias dwa kropka zero zamknięcie nawiasu" role="math"><math><mi>A</mi><mo>=</mo><mo>(</mo><mn>2</mn><mo>,</mo><mn>3</mn><mo>)</mo><mo>,</mo><mi>B</mi><mo>=</mo><mo>(</mo><mn>2</mn><mo>,</mo><mn>0</mn><mo>)</mo></math></span>, <span aria-label="A, równa się, nawias, minus, jeden kropka dwa zamknięcie nawiasu, przecinek, B, równa się, nawias dwa, przecinek, minus, jeden zamknięcie nawiasu" role="math"><math><mi>A</mi><mo>=</mo><mo>(</mo><mo>-</mo><mn>1</mn><mo>,</mo><mn>2</mn><mo>)</mo><mo>,</mo><mi>B</mi><mo>=</mo><mo>(</mo><mn>2</mn><mo>,</mo><mo>-</mo><mn>1</mn><mo>)</mo></math></span>, <span aria-label="A, równa się, nawias, minus, dwa kropka dwa zamknięcie nawiasu, przecinek, B, równa się, nawias trzy kropka dwa zamknięcie nawiasu" role="math"><math><mi>A</mi><mo>=</mo><mo>(</mo><mo>-</mo><mn>2</mn><mo>,</mo><mn>2</mn><mo>)</mo><mo>,</mo><mi>B</mi><mo>=</mo><mo>(</mo><mn>3</mn><mo>,</mo><mn>2</mn><mo>)</mo></math></span>, <span aria-label="A, równa się, nawias, minus, dwa, przecinek, minus, jeden zamknięcie nawiasu, przecinek, B, równa się, nawias trzy kropka jeden zamknięcie nawiasu" role="math"><math><mi>A</mi><mo>=</mo><mo>(</mo><mo>-</mo><mn>2</mn><mo>,</mo><mo>-</mo><mn>1</mn><mo>)</mo><mo>,</mo><mi>B</mi><mo>=</mo><mo>(</mo><mn>3</mn><mo>,</mo><mn>1</mn><mo>)</mo></math></span>
Narysujemy prostą o równaniu ogólnym .
Narysowanie tej prostej będzie łatwiejsze, jeśli zapiszemy ją w postaci kierunkowej: .
Z własności funkcji liniowej pamiętamy, że wykres funkcji przecina oś w punkcie o współrzędnych , a współczynnik kierunkowy jest równy .

- przecina oś w punkcie
- przecina oś w punkcie
- przechodzi przez punkt
Przeciągnij odpowiednie proste z dolnej sekcji do górnej.
<span aria-label="trzy x, plus, y, równa się, dwa" role="math"><math><mn>3</mn><mi>x</mi><mo>+</mo><mi>y</mi><mo>=</mo><mn>2</mn></math></span>, <span aria-label="początek ułamka, trzy, mianownik, pięć, koniec ułamka, x, plus, początek ułamka, jeden, mianownik, pięć, koniec ułamka, y, równa się, początek ułamka, cztery, mianownik, pięć, koniec ułamka" role="math"><math><mfrac><mn>3</mn><mn>5</mn></mfrac><mi>x</mi><mo>+</mo><mfrac><mn>1</mn><mn>5</mn></mfrac><mi>y</mi><mo>=</mo><mfrac><mn>4</mn><mn>5</mn></mfrac></math></span>, <span aria-label="dwa x, plus, dwa y, minus, dwa, równa się, zero" role="math"><math><mn>2</mn><mi>x</mi><mo>+</mo><mn>2</mn><mi>y</mi><mo>-</mo><mn>2</mn><mo>=</mo><mn>0</mn></math></span>, <span aria-label=" minus, x, minus, y, równa się, minus, jeden" role="math"><math><mo>-</mo><mi>x</mi><mo>-</mo><mi>y</mi><mo>=</mo><mo>-</mo><mn>1</mn></math></span>, <span aria-label="x, plus, y, równa się, jeden" role="math"><math><mi>x</mi><mo>+</mo><mi>y</mi><mo>=</mo><mn>1</mn></math></span>, <span aria-label="początek ułamka, jeden, mianownik, cztery, koniec ułamka, x, plus, początek ułamka, jeden, mianownik, cztery, koniec ułamka, y, minus, początek ułamka, jeden, mianownik, cztery, koniec ułamka, równa się, zero" role="math"><math><mfrac><mn>1</mn><mn>4</mn></mfrac><mi>x</mi><mo>+</mo><mfrac><mn>1</mn><mn>4</mn></mfrac><mi>y</mi><mo>-</mo><mfrac><mn>1</mn><mn>4</mn></mfrac><mo>=</mo><mn>0</mn></math></span>, <span aria-label="dwa x, plus, dwa y, plus, dwa, równa się, zero" role="math"><math><mn>2</mn><mi>x</mi><mo>+</mo><mn>2</mn><mi>y</mi><mo>+</mo><mn>2</mn><mo>=</mo><mn>0</mn></math></span>, <span aria-label="x, plus, początek ułamka, jeden, mianownik, trzy, koniec ułamka, y, równa się, początek ułamka, dwa, mianownik, trzy, koniec ułamka" role="math"><math><mi>x</mi><mo>+</mo><mfrac><mn>1</mn><mn>3</mn></mfrac><mi>y</mi><mo>=</mo><mfrac><mn>2</mn><mn>3</mn></mfrac></math></span>, <span aria-label="trzy x, plus, y, minus, dwa, równa się, zero" role="math"><math><mn>3</mn><mi>x</mi><mo>+</mo><mi>y</mi><mo>-</mo><mn>2</mn><mo>=</mo><mn>0</mn></math></span>
| proste pokryrywające się z prostą o równaniu | |
|---|---|
| proste pokrywające się z prostą o równaniu |
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
Zatem współrzędne wierzchołków to: 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. . : : oraz :
Zatem współrzędne wierzchołków to: 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. . : : oraz :
Zatem współrzędne wierzchołków to: 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. .
Uzasadnij, że nie istnieje wartość , dla której prosta jest prostopadła do osi .





