Rozwiązywanie równań z jedną niewiadomą

RbTywitNSLN3o

Czy wiesz, że za pomocą równań chciano przewidzieć pogodę?

ReRzi6V7x20gT

Na fotografii ukazany jest motyl o beżowo‑czarnym ubarwieniu. Motyl siedzi na kwiatku w kolorze fioletowym. Ten kwiat to cynia. Tło jest ciemne, rozmyte. — Źródło: dostępny w internecie: Pexels.com, domena publiczna.

W $1963$ roku Edward Norton Lorenz amerykański matematyk i meteorolog opracował równania opisujące zależności między parametrami pogody. Wydawało mu się, że jeżeli wykorzysta komputer do rozwiązania tych równań, to będzie można przewidzieć pogodę z dużą dokładnością. Okazało się jednak, że nawet niewielka zmiana jednej liczby w którymś z równań powoduje otrzymanie bardzo różnych wyników. Lorenz udowodnił w ten sposób, że niewielka zmiana w jednym z punktów atmosfery może być przyczyną ogromnych zmian w innym jej obszarze. Nazwano to „efektem motyla” – ruch skrzydeł motyla nad Amazonką, może wywołać burzę w Karolinie Północnej w USA. Lorenz udowodnił więc, że przewidywanie pogody długofalowej w oparciu o naukę jest niemożliwe.

Równania, które stworzył Lorenz były bardzo skomplikowane, zawierały wiele niewiadomych. My ograniczymy się do rozpatrywania w tym materiale, równań tylko z jedną niewiadomą.

Interaktywna treść merytorycznaInteraktywna treść merytoryczna
Ilustracja interaktywnaIlustracja interaktywna
Zestaw ćwiczeń interaktywnychZestaw ćwiczeń interaktywnych
SłownikSłownik

Twoje cele

Przekształcisz równoważnie równanie.
Rozwiążesz równanie z jedną niewiadomą metodą równań równoważnych.
Określisz rodzaj równania.

RównaniemRównanieRównaniem nazywamy dwa wyrażenia algebraiczne (z których przynajmniej jedno zawiera literę) połączone znakiem „ $=$ ”.

Wyrażenia występujące po obu stronach znaku „ $=$ ” nazywamy stronami równania, a wyrażenia algebraiczne występujące w równaniu nazywamy jego wyrazami.

R10UzdbFWB3i4

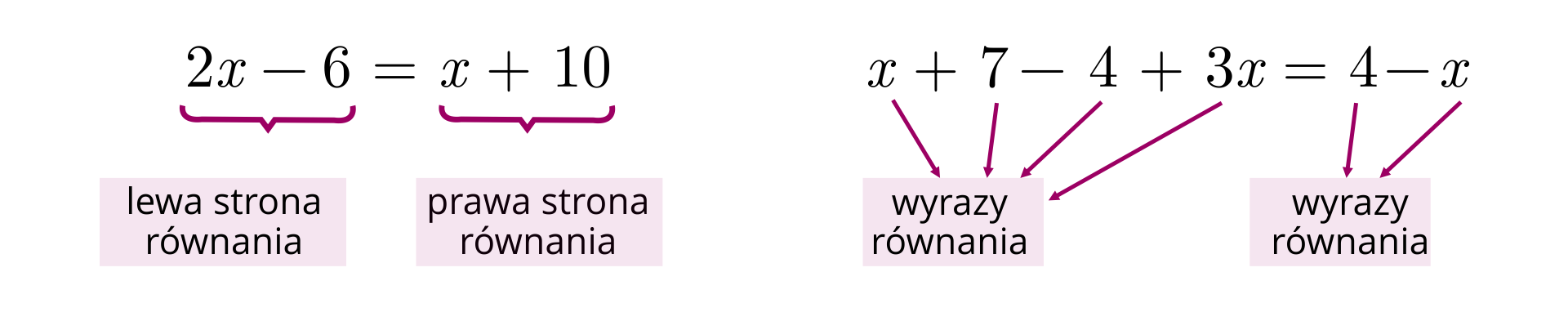
Po lewej stronie grafiki znajduje się zapis matematyczny 2x-6=x+10. Za pomocą klamry zaznaczono 2x‑6 i podpisano jako: "lewa strona równania". Tak samo zaznaczono człon x+10. Podpisano go jako: "prawa strona równania". Po prawej stronie ekranu znajduje się następujący zapis matematyczny: x+7‑4+3x=4‑x. Od każdego elementu składowego równania po lewej stronie poprowadzono prostą, na końcu której znajduje się podpis: "wyrazy równania". Od każdego elementu składowego równania po prawej stronie także poprowadzono prostą, na końcu której znajduje się podpis: "wyrazy równania". — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Grafika przedstawia dwa równania. Po lewej stronie grafiki znajduje się równanie: $2 x - 6 = x + 10$ . Za pomocą klamry zaznaczono $2 x - 6$ i podpisano jako: „lewa strona równania”. Tak samo zaznaczono człon $x + 10$ . i podpisano go jako: „prawa strona równania”. Po prawej stronie ekranu znajduje się drugie równanie: $x + 7 - 4 + 3 x = 4 - x$ . Od każdego elementu składowego lewej strony równania poprowadzono strzałkę, na końcu której znajduje się podpis: „wyrazy równania”. Od każdego elementu składowego prawej strony równania także poprowadzono strzałkę, na końcu której znajduje się podpis: „wyrazy równania”.

Przykład 1

Określimy wyrazy równania: $8 x + 10 - x + 2 = x - 3$ .

Wyrazy równania: $8 x$ , $10$ , $(- x)$ , $2$ , $x$ , $(- 3)$ .

Litery występujące w równaniu nazywamy niewiadomymi. Jeżeli w równaniu występuje tylko jedna niewiadoma, to równanieRównanierównanie nazywamy równaniem z jedną niewiadomą. Jeśli niewiadoma ta występuje w pierwszej potędze, to równanie nazywamy równaniem pierwszego stopnia z jedną niewiadomą.


Równania pierwszego stopnia z jedną niewiadomą	Równania, które nie są równaniami pierwszego stopnia z jedną niewiadomą
$4 x - 2 = x + 1$ $4 - a + 1 = 0$	$4 x - 2 = y + 1$ $4 x^{2} - 2 = x + 1$

Mówimy, że dana liczba spełnia równanieRównanierównanie, jest rozwiązaniem równania lub pierwiastkiem równania, jeżeli po podstawieniu jej w miejsce niewiadomej otrzymujemy równość prawdziwą.

Przykład 2

Sprawdzimy, że liczba $4$ jest rozwiązaniem równania $2 x - 2 = x + 2$ .

Podstawiamy liczbę $4$ do prawej i lewej strony równania w miejsce niewiadomej $x$ .

L = 2 \cdot 4 - 2 = 8 - 2 = 6

P = 4 + 2 = 6

L = P

Zbiór wszystkich liczb spełniających dane równanieRównanierównanie, nazywamy zbiorem rozwiązań równania.

Równania nazywamy równoważnymi, gdy mają ten sam zbiór rozwiązań. Pokażemy teraz sposoby rozwiązywania równań metodą równań równoważonych. Metoda ta pozwala w prosty sposób wyznaczyć niewiadomą, przekształcając kolejno dane równanieRównanierównanie na prostsze równania równoważne.

Aby otrzymać równanie równoważneRównanie równoważnerównanie równoważne danemu, obie strony równania możemy przekształcić, stosując prawa działań lub przeprowadzając redukcję wyrazów podobnych.

Przykład 3

Rozwiążemy równanieRównanierównanie $4 (x - 3) - 3 (x - 4) = 7$ .

4 (x - 3) - 3 (x - 4) = 7

4 x - 12 - 3 x + 12 = 7

– wykonaliśmy wskazane działania

x = 7

– przeprowadziliśmy redukcję wyrazów podobnych

Odpowiedź:
Rozwiązaniem równania jest liczba $7$ .

Równanie równoważneRównanie równoważneRównanie równoważne danemu możemy też otrzymać, mnożąc lub dzieląc obie strony równania przez tę samą liczbę różną od zera.

Przykład 4

Rozwiążemy równanieRównanierównanie $4 x = 20$ .

Sposób $1$ :
Mnożymy obie strony równania przez $\frac{1}{4}$ .

4 x = 20 | \cdot \frac{1}{4}

\frac{1}{4} \cdot 4 \cdot x = \frac{1}{4} \cdot 20

x = 5

Sposób $2$ :
Dzielimy obie strony równania przez $4$ .

(4 \cdot x) : 4 = 20 : 4

x = 5

Odpowiedź:
Rozwiązaniem równania jest liczba $5$ .

Równanie równoważneRównanie równoważneRównanie równoważne danemu otrzymamy, jeżeli do obu stron równania (lub od obu stron równania) dodamy (odejmiemy) to samo wyrażenie.

Przykład 5

Znajdziemy rozwiązanie równania $2 x - 6 = x + 10$ .

W równaniu tym niewiadome występują po obu stronach równania. Będziemy tak przekształcać równoważnie równanie, aby po jednej stronie równania otrzymać niewiadomą, a po drugiej wiadome.

2 x - 6 = x + 10

2 x - 6 - x = x + 10 - x

– od obu stron równania odejmujemy

x

x - 6 = 10

– zredukowaliśmy wyrazy podobne

x - 6 + 6 = 10 + 6

– do obu stron dodajemy

6

x = 16

– zredukowaliśmy wyrazy podobne

Odpowiedź:
Rozwiązaniem równania jest liczba $16$ .

Przykład 6

Rozwiążemy równanie $2 (x + 1) - 2 = 16 - 3 (x + 2)$ .

2 (x + 1) - 2 = 16 - 3 (x + 2)

2 x + 2 - 2 = 16 - 3 x - 6

– wykonaliśmy mnożenie

2 x = 10 - 3 x

– zredukowaliśmy wyrazy podobne

2 x + 3 x = 10 - 3 x + 3 x

– do obu stron równania dodajemy

3 x

5 x = 10

– zredukowaliśmy wyrazy podobne

5 x : 5 = 10 : 5

– dzielimy obie strony równania przez

5

x = 2

Odpowiedź:
Rozwiązaniem równania jest liczba $2$ .

Równania, które dotychczas rozwiązywaliśmy miały zawsze jedno rozwiązanie. Takie równania nazywamy oznaczonymi. Są też równania, które mają nieskończenie wiele rozwiązań. Takie równania nazywamy tożsamościowymi.

Przykład 7

Rozwiążemy równanie $6 - 3 (x - 5) = 3 (7 - x)$ .
Wykonujemy wskazane działania i redukujemy wyrazy podobne.

6 - 3 (x - 5) = 3 (7 - x)

6 - 3 x + 15 = 21 - 3 x | - 6 - 15

6 - 3 x + 15 - 6 - 15 = 21 - 3 x - 6 - 15

- 3 x = - 3 x | + 3 x

- 3 x + 3 x = - 3 x + 3 x

0 = 0

Otrzymaliśmy równość arytmetyczną.

Odpowiedź:
Każda liczba spełnia to równanieRównanierównanie. Równanie ma nieskończenie wiele rozwiązań.

Nie każde równanie ma rozwiązanie. Równania, które nie mają rozwiązań nazywamy sprzecznymi.

RWbfPSCoQzl0o

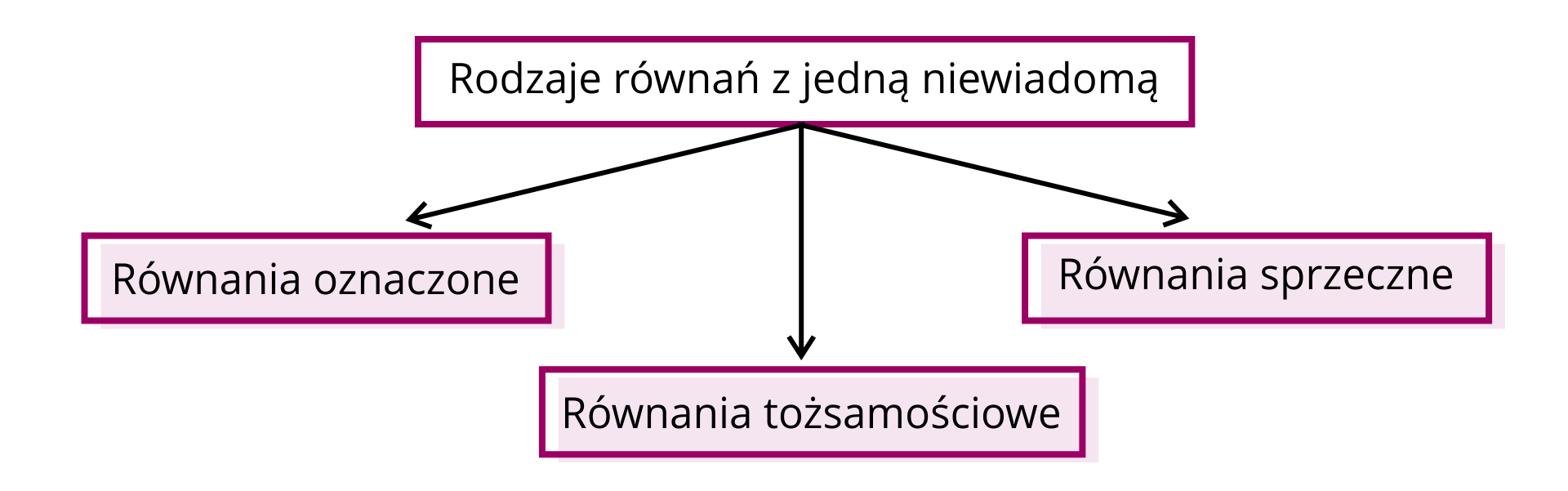
Grafika przedstawia schemat składający się z czterech ramek. Od fioletowej ramki z napisem "Rodzaje równań z jedną niewiadomą" poprowadzone są trzy strzałki. Grot każdej z nich wskazuje na kolejną ramkę. W pierwszej ramce jest tekst "Równania oznaczone", w drugiej "Równania tożsamościowe", w trzeciej "Równania sprzeczne". — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Przykład 8

Przykłady równań oznaczonych.

$2 m - 1 = m + 4$
$2 m - 1 = m + 4 | - m$
$2 m - m - 1 = m + 4 - m$
$m - 1 = 4 | + 1$
$m - 1 + 1 = 4 + 1$
$m = 5$
$3 (x - 2) + 6 = 0$
$3 x - 6 + 6 = 0$
$3 x = 0 | : 3$
$x = 0$
$4 - (- x - 4) - 4 = - x$
$4 + x + 4 - 4 = - x$
$4 + x = - x | + x$
$4 + x + x = - x + x$
$2 x + 4 = 0 | - 4$
$2 x + 4 - 4 = 0 - 4$
$2 x = - 4 | : 2$
$x = - 2$
$2 (1 + x) - 2 (x - 1) = x - 4$
$2 + 2 x - 2 x + 2 = x - 4$
$4 = x - 4 | + 4$
$4 + 4 = x - 4 + 4$
$8 = x$

Przykład 9

Przykłady równań tożsamościowych.

$a + 4 = 4 + a$
$a + 4 = 4 + a | - a - 4$
$a + 4 - a - 4 = 4 + a - a - 4$
$0 = 0$
Równanie ma nieskończenie wiele rozwiązań.
$2 (5 - 3 a) + 4 = 2 (7 - 3 a)$
$10 - 6 a + 4 = 14 - 6 a$
$14 - 6 a = 14 - 6 a | - 14 + 6 a$
$14 - 14 + 6 a - 6 a = 14 - 6 a - 14 + 6 a$
$0 = 0$
Równanie ma nieskończenie wiele rozwiązań.
$(a - 1) \cdot (- 1) = (1 - a) (- 1) - 2 (a - 1)$
$- a + 1 = - 1 + a - 2 a + 2$
$- a + 1 = - a + 1 | + a - 1$
$- a + 1 + a - 1 = - a + 1 + a - 1$
$0 = 0$
Równanie ma nieskończenie wiele rozwiązań.
$3 - (- a - 1) = a + 4$
$3 + a + 1 = a + 4 | - a - 4$
$4 + a - a - 4 = a + 4 - a - 4$
$0 = 0$
Równanie ma nieskończenie wiele rozwiązań.

Przykład 10

Przykłady równań sprzecznych.

$y + 6 = 2 y - (5 + y)$
$y + 6 = 2 y - 5 - y$
$y + 6 = y - 5 | + 5 - y$
$y + 6 + 5 - y = y - 5 + 5 - y$
$11 = 0$ - sprzeczność
Równanie nie ma rozwiązania.
$y + 1 = y | - 1 - y$
$y + 1 - 1 - y = y - 1 - y$
$0 = - 1$ - sprzeczność
Równanie nie ma rozwiązania.
$- (y + 3) + y = 0$
$- y - 3 + y = 0$
$- 3 = 0$ - sprzeczność
Równanie nie ma rozwiązania.
$3 (1 - y) + 2 = 3 - 3 (y - 1)$
$3 - 3 y + 2 = 3 - 3 y + 3$
$5 - 3 y = 6 - 3 y | + 3 y$
$5 - 3 y + 3 y = 6 - 3 y + 3 y$
$5 = 6$ - sprzeczność
Równanie nie ma rozwiązania.

Przykład 11

Rozwiążemy równanie.

x - 3 + 2 x = x + 4 + x

Redukujemy wyrazy podobne po obu stronach równania.

3 x - 3 = 2 x + 4

Do obu stron równania dodajemy $3$ .

3 x - 3 + 3 = 2 x + 4 + 3

Redukujemy wyrazy podobne.

3 x = 2 x + 7

Od obu stron równania odejmujemy $2 x$ , aby po lewej stronie równania otrzymać niewiadome.

3 x - 2 x = 2 x + 7 - 2 x

Redukujemy wyrazy podobne.

x = 7

Odpowiedź:
Rozwiązaniem równania jest liczba $7$ .

Przykład 12

Rozwiążemy równanie.

4 x + 1 = x - 2 (1 - 2 x)

Po prawej stronie równania wykonujemy mnożenie.

4 x + 1 = x - 2 + 4 x

Redukujemy wyrazy podobne po prawej stronie równania.

4 x + 1 = 5 x - 2

Do obu stron równania dodajemy $(2 - 4 x)$ .

4 x + 1 + 2 - 4 x = 5 x - 2 + 2 - 4 x

Redukujemy wyrazy podobne.

3 = x

Odpowiedź:
Rozwiązaniem równania jest liczba $3$ .

Przykład 13

Rozwiążemy równanie.

1 - (2 - x) - (3 + x) = 5 - (1 - 2 x)

Opuszczamy nawiasy po obu stronach równania.

1 - 2 + x - 3 - x = 5 - 1 + 2 x

Redukujemy wyrazy podobne.

- 4 = 4 + 2 x

Od obu stron równania odejmujemy $4$ .

- 4 - 4 = 4 - 4 + 2 x

Redukujemy wyrazy podobne.

- 8 = 2 x

Dzielimy obie strony równania przez $2$ .

- 8 = 2 x | : 2

- 4 = x

Odpowiedź:
Rozwiązaniem równania jest liczba $(- 4)$ .

Przykład 14

Rozwiążemy równanie.

2 (x - 1) - 2 (1 + x) = 3 (x - 1) - 4

Po obu stronach równania wykonujemy mnożenie.

2 x - 2 - 2 - 2 x = 3 x - 3 - 4

Redukujemy wyrazy podobne po obu stronach równania.

- 4 = 3 x - 7

Do obu stron równania dodajemy $7$ .

- 4 + 7 = 3 x - 7 + 7

Redukujemy wyrazy podobne.

3 = 3 x

Dzielimy obie strony równania przez $3$ .

3 = 3 x | : 3

1 = x

Odpowiedź:
Rozwiązaniem równania jest liczba $1$ .

Przykład 15

Rozwiążemy równanie.

4 - (x - 6) + 2 (x + 1) = 5 (x - 1) + 3 (1 - x) - x

Wykonujemy mnożenie, opuszczamy nawiasy.

4 - x + 6 + 2 x + 2 = 5 x - 5 + 3 - 3 x - x

Redukujemy wyrazy podobne.

12 + x = x - 2

Odejmujemy od obu stron równania $x$ .

12 + x - x = x - 2 - x

12 = - 2

Otrzymaliśmy równość arytmetyczną sprzeczną.

Odpowiedź:
Równanie nie ma rozwiązania.

W przypadku gdy rozwiązanie równania wymaga wielu przekształceń, łatwo pomylić się w obliczeniach. Warto więc wtedy sprawdzić, czy znaleziona liczba jest rzeczywiście rozwiązaniem równania.

Przykład 16

Rozwiążemy równanie $- [2 (3 - x) + 2] : 2 = 3 [4 (x + 1) - 2 (x - 1)] + (x + 2)$ i wykonamy sprawdzenie.

- [2 (3 - x) + 2] : 2 = 3 [4 (x + 1) - 2 (x - 1)] + (x + 2)

Wykonujemy najpierw działania w nawiasach kwadratowych.

- [6 - 2 x + 2] : 2 = 3 [4 x + 4 - 2 x + 2] + (x + 2)

- (8 - 2 x) : 2 = 3 (2 x + 6) + (x + 2)

Wykonujemy dzielenie po lewej stronie, a po prawej – mnożenie.

- 4 + x = 6 x + 18 + x + 2

Przekształcamy tak równanie, aby po prawej stronie otrzymać wyrażenia z niewiadomą, a po lewej wiadome.

- 4 + x = 7 x + 20 | - 20 - x

- 4 + x - 20 - x = 7 x + 20 - 20 - x

- 24 = 6 x | : 6

- 4 = x

Sprawdzenie:

Do obu stron równania w miejsce $x$ wystawiamy $(- 4)$ .

L = - \{2 [3 - (- 4)] + 2\} : 2 = - [2 \cdot 7 + 2] : 2

L = - 16 : 2 = - 8

P = 3 [4 (- 4 + 1) - 2 (- 4 - 1)] + (- 4 + 2)

P = 3 [4 \cdot (- 3) - 2 (- 5)] + (- 2)

P = 3 (- 12 + 10) - 2

P = 3 \cdot (- 2) - 2 = - 6 - 2 = - 8

Wartości wyrażeń po obu stronach równania są równe.

P = L

Wyznaczona liczba jest rozwiązaniem równania.

Odpowiedź:
Rozwiązaniem równania jest liczba $(- 4)$ .

Przykład 17

Rozwiążemy równanie, opisując kolejne kroki rozwiązania.

- [- (x - 1) + (x - 1)] - 1 = - (1 - x) + (x - 1) + 1

Rozwiązanie:

- [- (x - 1) + (x - 1)] - 1 = - (1 - x) + (x - 1) + 1

Opuszczamy nawiasy zwykłe.

- (- x + 1 + x - 1) - 1 = - 1 + x + x - 1 + 1

Redukujemy wyrazy podobne.

- 1 = 2 x - 1

Dodajemy do obu stron liczbę $1$ .

0 = 2 x

Dzielimy obie strony równania przez $2$ .

0 = x

Odpowiedź:
Rozwiązaniem równania jest liczba $0$ .

Notatki

RoHtAjXsObFdl

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ilustracja interaktywna

R8xVm9Cky0Lm6

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ilustracja interaktywna przedstawia tablicę szkolną, na której zapisano równania. Na ilustracji znajduje się dwanaście punktów interaktywnych, po kliknięciu, w które wyświetla się ramka z tekstem oraz nagraniem głosowym z nim tożsamym.

Pierwszy punkt znajduje się nad równaniami w kolorze żółtym, jego treść jest następująca: równania z kilkoma niewiadomymi. W równaniach po obu stronach znaku równości występują wyrażenia algebraiczne. Wyrażenia te zawierają litery, oznaczające liczby, których nie znamy. Nazywamy je niewiadomymi. W każdym z tych równań występują co najmniej dwie litery. Są to równania z kilkoma niewiadomymi.
Drugi punkt znajduje się po prawej stronie, nad równaniami w kolorze niebieskim, jego treść brzmi: równania z jedną niewiadomą. W każdym z tych równań występuje tylko jedna niewiadoma. Są to równania z jedną niewiadomą.
Trzeci punkt znajduje się nad równaniami w kolorze pomarańczowym jego treść jest następująca: równania pierwszego stopnia z jedną niewiadomą. W każdym z tych równań jest jedna niewiadoma i ta niewidoma występuje w pierwszej potędze. Są to równania pierwszego stopnia z jedną niewiadomą.
Punkty cztery, pięć oraz sześć przedstawiają równania należące do grupy równań z kilkoma niewiadomymi.
$m + 5 x - 3 = 2 (x - m)$ Jest to równanie z niewiadomymi $x$ oraz $m$ .
$a - b - c = 0, 3 d$ Jest to równanie z czterema niewiadomymi: $a$ , $b$ , $c$ , $d$ .
$a^{4} + (4 x - 2 y) : 3 = 0$ Jest to równanie z trzema niewiadomymi: $a$ , $x$ , $y$ .
Kolejne trzy punkty, czyli siedem, osiem i dziewięć należą do równań z jedną niewiadomą.
$a - 5 = a^{3}$ Jest to równanie z niewiadomą $a$ , występującą w trzeciej potędze. Jest to równanie stopnia trzeciego z jedną niewiadomą.
$k (k + 2 k) = 0$ Jest to równanie stopnia drugiego z jedną niewiadomą $k$ .
$\frac{1, 2 - m^{4}}{m} = 2$ Równanie z niewiadomą $m$ , występującą w czwartej potędze. Jest to równanie stopnia czwartego z jedną niewiadomą.
Ostatnie trzy równania, należą do równań pierwszego stopnia z jedną niewiadomą.
$3 x - 6 = 0$ Rozwiązaniem tego równania jest liczba $2$ .
Rzeczywiście:
$3 x - 6 = 0$
$3 x - 6 = 0 | + 6$
$3 x - 6 + 6 = 0 + 6$
$3 x = 6 | : 3$
$\frac{3 x}{3} = \frac{6}{3}$
$x = 2$
$a - 6 (a - 1) = 6 - 5 a$ Jest to równanie tożsamościowe. Każda liczba rzeczywista spełnia to równanie.
Rzeczywiście:
$a - 6 (a - 1) = 6 - 5 a$
$a - 6 a + 6 = 6 - 5 a$
$- 5 a + 6 = 6 - 5 a | - 6 + 5 a$
$- 5 a + 6 - 6 + 5 a = 6 - 5 a - 6 + 5 a$
$0 = 0$
Otrzymana równość jest zawsze prawdziwa.
$5 - 4 y = 4 (1 - y) + 4$ Żadna liczba nie spełnia tego równania. Takie równanie nazywamy sprzecznym. To równanie nie ma więc rozwiązania.
Rzeczywiście:
$5 - 4 y = 4 (1 - y) + 4$
$5 - 4 y = 4 - 4 y + 4$
$5 - 4 y = - 4 y | + 4 y$
$5 - 4 y + 4 y = - 4 y + 4 y$
$5 = 0$
Otrzymaliśmy sprzeczność. Równanie nie ma rozwiązania.

Polecenie 1

Zapoznaj się z ilustracją interaktywną i na jej podstawie wskaż równaniaRównanierównania, które nie są równaniami pierwszego stopnia z jedną niewiadomą.

$3 x - 4 y = x - y$
${(a + 1)}^{2} - 5 = a - 2$
$m - 1 = m^{3}$
$(x - 1) (2 - 8) = x$
$9 - k = 6 k + 1 - k$

Ry7bEeqNeAwlC

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Polecenie 2

Jakie wyrażenie należy wstawić w miejsce $A$ , aby otrzymać równanieRównanierównanie tożsamościowe?

4 (x - 1) + 3 (2 + x) = 5 x + A

R1W5AvNhhUUIZ

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

A = 2 x + 2

Polecenie 3

Podaj sformułowanie, które należy wpisać w miejsce kropek.

Równanie sprzeczne to równanieRównanierównanie, które ...

RvR4etxOTK6Zw

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Zestaw ćwiczeń interaktywnych

RK3R6oYlfRRTd

Ćwiczenie 1

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ry5wv2IwcsZ5j

Ćwiczenie 2

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

R1bYf5pS9fYQs

Ćwiczenie 3

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ćwiczenie 4

RNSBUM8RgpSoL

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Jeżeli $6 x = 9$ to $x = \frac{3}{2}$ .
Jeżeli $x + 1 = 5$ to $x = 4$ .
Jeżeli $x - 1 = - 2$ to $x = - 1$ .
Jeżeli $4 x + 1 = x - 6$ to $x = - \frac{7}{3}$ .
Jeżeli $x : 10 = 5$ to $x = 50$ .

Ćwiczenie 5

RNsFPir9sgoBw

Połącz w pary równania równoważne.

2 (3 - a) - 6 = 4 - (a - 1)

Możliwe odpowiedzi: 1.

2 a = 5 - a

, 2.

- 2 a + 12 = 3 + a

, 3.

2 a = 3 - a

, 4.

- 2 a = 5 - a

, 5.

- 12 - 2 a = a + 5

- 2 (3 - a) + 6 = 4 - (a + 1)

Możliwe odpowiedzi: 1.

2 a = 5 - a

, 2.

- 2 a + 12 = 3 + a

, 3.

2 a = 3 - a

, 4.

- 2 a = 5 - a

, 5.

- 12 - 2 a = a + 5

2 (3 + a) - 6 = 4 - (a - 1)

Możliwe odpowiedzi: 1.

2 a = 5 - a

, 2.

- 2 a + 12 = 3 + a

, 3.

2 a = 3 - a

, 4.

- 2 a = 5 - a

, 5.

- 12 - 2 a = a + 5

2 (3 - a) + 6 = 4 + (a - 1)

Możliwe odpowiedzi: 1.

2 a = 5 - a

, 2.

- 2 a + 12 = 3 + a

, 3.

2 a = 3 - a

, 4.

- 2 a = 5 - a

, 5.

- 12 - 2 a = a + 5

- 2 (3 + a) - 6 = 4 + (a + 1)

Możliwe odpowiedzi: 1.

2 a = 5 - a

, 2.

- 2 a + 12 = 3 + a

, 3.

2 a = 3 - a

, 4.

- 2 a = 5 - a

, 5.

- 12 - 2 a = a + 5

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ćwiczenie 6

ROAaSM6QEh2vh

Łączenie par. Oceń prawdziwość podanych zdań. Zaznacz Prawda - jeżeli zdanie jest prawdziwe, Fałsz - jeżeli jest fałszywe.. Redukując po każdej stronie równania

8 + 4 x - x - 3 = 5 x - 6 - 5 x

wyrazy podobne otrzymujemy

3 x + 5 = - 6

.. Możliwe odpowiedzi: Prawda, Fałsz. Wykonując po każdej stronie równania

10 - 6 (2 - x) = 5 (1 + x) - 3

mnożenie otrzymujemy

10 - 12 + 6 x = 5 + 5 x - 3

.. Możliwe odpowiedzi: Prawda, Fałsz. Po wykonaniu dzielenia w równaniu

(10 x - 5) : 5 = 2 x

otrzymujemy

2 x - 5 = 2 x

.. Możliwe odpowiedzi: Prawda, Fałsz. Opuszczając nawiasy po każdej stronie równania

(4 - x) - (x - 1) = - (3 x - 4)

otrzymujemy

4 - x - x - 1 = - 3 x + 4

.. Możliwe odpowiedzi: Prawda, Fałsz

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ćwiczenie 7

R1WrE5lcSdQsM

Przeciągnij równania na odpowiednie pola. Równania oznaczone: Możliwe odpowiedzi: 1.

- x + (x - 1) + 1 = 0

, 2.

x + (x - 1) + 1 = 2 x

, 3.

- [x - (x - 1)] + 1 = 0

, 4.

x - (x - 1) + 1 = x

, 5.

x + (x - 1) + 1 = 0

, 6.

- [x - (x - 1)] + x = x

, 7.

- [x + (x - 1)] + 1 = 0

, 8.

2 [x - (x - 1)] + 1 = 0

Równania tożsamościowe: Możliwe odpowiedzi: 1.

- x + (x - 1) + 1 = 0

, 2.

x + (x - 1) + 1 = 2 x

, 3.

- [x - (x - 1)] + 1 = 0

, 4.

x - (x - 1) + 1 = x

, 5.

x + (x - 1) + 1 = 0

, 6.

- [x - (x - 1)] + x = x

, 7.

- [x + (x - 1)] + 1 = 0

, 8.

2 [x - (x - 1)] + 1 = 0

Równania sprzeczne: Możliwe odpowiedzi: 1.

- x + (x - 1) + 1 = 0

, 2.

x + (x - 1) + 1 = 2 x

, 3.

- [x - (x - 1)] + 1 = 0

, 4.

x - (x - 1) + 1 = x

, 5.

x + (x - 1) + 1 = 0

, 6.

- [x - (x - 1)] + x = x

, 7.

- [x + (x - 1)] + 1 = 0

, 8.

2 [x - (x - 1)] + 1 = 0

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ćwiczenie 8

Wykaż, że równanie $[2 (3 x - 4) - (- x - 1)] : 7 + 1 = - 3 (2 + x) + 4 x$ nie ma rozwiązania.

R1Mx2IPbDLSD0

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

[2 (3 x - 4) - (- x - 1)] : 7 + 1 = - 3 (2 + x) + 4 x

(6 x - 8 + x + 1) : 7 + 1 = - 6 - 3 x + 4 x

(7 x - 7) : 7 + 1 = x - 6

x - 1 + 1 = x - 6

x = x - 6

x - x = x - x - 6

0 = - 6

Ćwiczenie 9

Rozwiąż równanie.

$8 - 3 x = 3 + 2 x$
$5 x - x + 1 = 11 - 2 (x - 1)$
$7 (x - 1) - 6 (1 - x) = 0$

RxzXkNLOUmlIC

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Do obu stron dodaj $3 x - 3$ .
Po prawej stronie wykonaj mnożenie, po lewej zredukuj wyrazy podobne.
Wykonaj mnożenie i zredukuj wyrazy podobne.

$8 - 3 x = 3 + 2 x$
$8 - 3 = 2 x + 3 x$
$5 = 5 x | : 5$
$x = 1$
$5 x - x + 1 = 11 - 2 (x - 1)$
$4 x + 1 = 11 - 2 x + 2 | + 2 x - 1$
$4 x + 2 x = 13 - 1$
$6 x = 12 | : 6$
$x = 2$
$7 (x - 1) - 6 (1 - x) = 0$
$7 x - 7 - 6 + 6 x = 0$
$13 x - 13 = 0$
$13 x = 13 | : 13$
$x = 1$

Ćwiczenie 10

Wykaż, że równanie $5 - 3 (1 - 4 x) + 2 (3 - 6 x) = 0$ nie ma rozwiązania.

R1eLstmu20KkI

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

5 - 3 (1 - 4 x) + 2 (3 - 6 x) = 0

Wykonujemy wskazane działania.

5 - 3 + 12 x + 6 - 12 x = 0

Redukujemy wyrazy podobne.

8 = 0

Równość arytmetyczna nieprawdziwa, równanie nie ma rozwiązania.

Ćwiczenie 11

Wykaż, że równanie $- (2 x - 3) + 2 (x + 1) = 5$ ma nieskończenie wiele rozwiązań.

RgUM3i3AfjBGm

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

- (2 x - 3) + 2 (x + 1) = 5

Wykonaj wskazane działania.

- 2 x + 3 + 2 x + 2 = 5

Zredukuj wyrazy podobne.

5 = 5

Równość arytmetyczna prawdziwa – równanie ma niekończenie wiele rozwiązań.

Słownik

równanie

dwa wyrażenie algebraiczne (z których przynajmniej jedno zawiera literę) połączone znakiem „ $=$ ”.

równanie równoważne

równania mające ten sam zbiór rozwiązań.

Bibliografia

Polya G., (2009), Jak to rozwiązać?, Warszawa: Wydawnictwo Naukowe PWN.