Rozwiązywanie zadania tekstowego za pomocą równania

Za $5 \mathrm{kg}$ cebuli i $2 \mathrm{kg}$ ziemniaków zapłacono $19 \mathrm{zł}$. Cena $1 \mathrm{kg}$ ziemniaków była o $1 \mathrm{zł}$ mniejsza od ceny $1 \mathrm{kg}$ cebuli. Ile zapłacono za ziemniaki, a ile za cebulę?

R1XIWmrNY3Ohb

Po lewej stronie grafiki umieszczone jest zdjęcie białej cebuli ułożonej luzem. Powyżej znajduje się zapis: "$5 \mathrm{kg}$", a poniżej: "$x \mathrm{zł}$". Po prawej stronie grafiki znajduje się zdjęcie ziemniaków ułożonych w kilku kobiałkach. Nad fotografią umieszczony jest napis: "$2 \mathrm{kg}$", a poniżej jest zapis: "$\left(x-1\right) \mathrm{zł}$". W centralnej części ekranu umiejscowione jest białe kółko z zieloną obwódką. W kółku jest napis: "$19 \mathrm{zł}$".

Analiza zadania:
$x$ – cena cebuli (w $\mathrm{zł}$),
$\left(x-1\right)$ – cena ziemniaków (w $\mathrm{zł}$),
$5x$ – wartość kupionej cebuli (w $\mathrm{zł}$),
$2\left(x-1\right)$ – wartość zakupionych ziemniaków.
Układamy i rozwiązujemy równanie.

Wykonujemy mnożenie i redukujemy wyrazy podobne.

Do obu stron równania dodajemy $2$ i obie strony dzielimy przez $7$.

Obliczamy cenę ziemniaków.

Obliczamy ile zapłacono za ziemniaki, a ile za cebulę.
$2·2=4 \left(\mathrm{zł}\right)$
$5·3=15 \left(\mathrm{zł}\right)$

Odpowiedź:
Za ziemniaki zapłacono $4 \mathrm{zł}$, a za cebulę $15 \mathrm{zł}$.

Połowa znajomych Oli gra w koszykówkę, trzecia część znajomych gra w siatkówkę, a pozostałych $8$ osób trenuje pływanie. Ilu znajomych ma Ola?

R1aXTnXkuWEH4

Po lewej stronie grafiki umieszczone jest zdjęcie grupy młodych dziewcząt, które grają w koszykówkę. Pod fotografią znajduje się zapis: "$\frac{1}{2}x$". W centralnej części jest zdjęcie przedstawiające młodych chłopaków grających w piłkę siatkową. Poniżej jest zapis: "$\frac{1}{3}x$". Po prawej stronie grafiki umieszczone jest zdjęcie pływaka w basenie sportowym, a pod nim znajduje się liczba $8$. Wszystkie trzy zdjęcia objęte są jedną, wspólną klamrą, przy której znajduje się napis: "$x$".

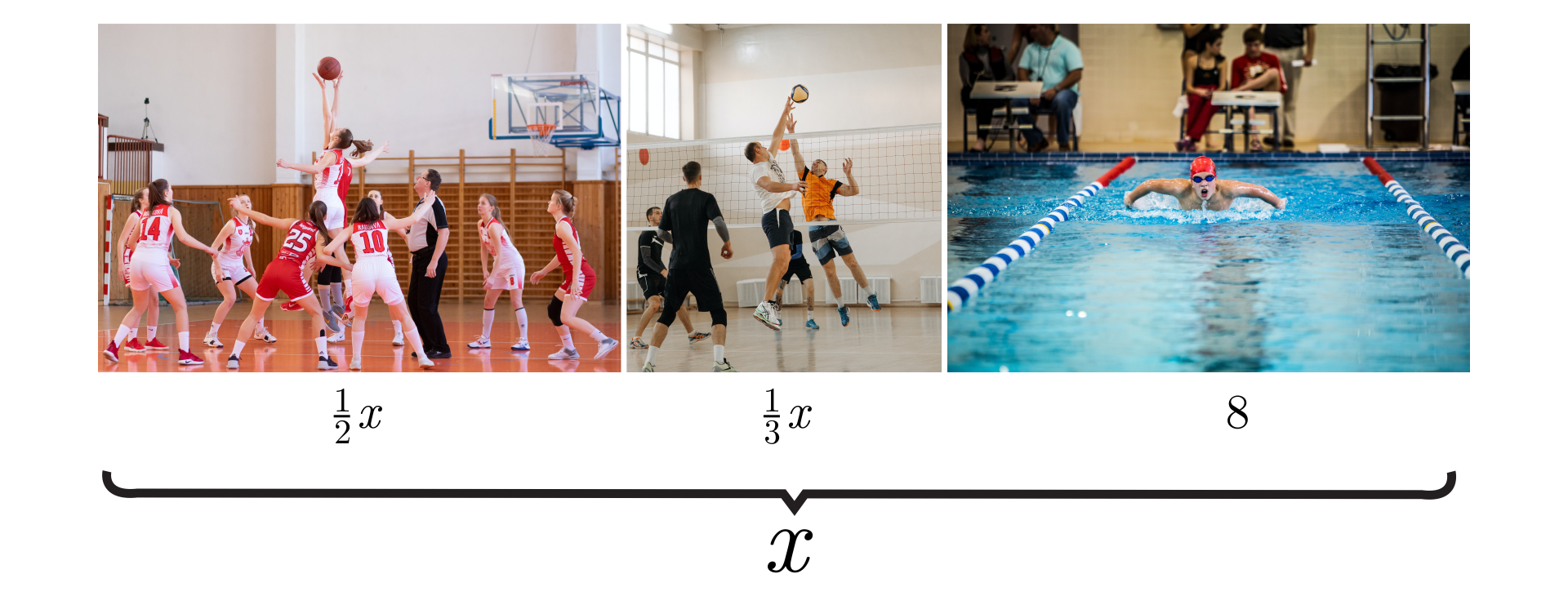
Analiza zadania:
$x$ – liczba znajomych Oli,
$\frac{1}{2}x$ – tylu znajomych gra w koszykówkę,
$\frac{1}{3}x$ – tylu znajomych gra w siatkówkę,
$8$ – tylu znajomych trenuje pływanie.
Zwróć uwagę, że liczba $x$ musi być liczbą naturalną (jako liczba znajomych Oli).
Układamy i rozwiązujemy równanie.

Mnożymy obie strony równania przez $6$ (najmniejsza wspólna wielokrotność liczb $2$ i $3$).

Redukujemy wyrazy podobne i odejmujemy od obu stron równania $5x$.

Znaleziona liczb jest liczbą naturalną, zatem spełnia warunki zadania.

Odpowiedź:
Ola ma $48$ znajomych.

W prawej szufladzie było $5$ razy więcej zielonych kulek niż w lewej. Z prawej szuflady przełożono do lewej $18$ kulek i teraz w lewej szufladzie jest dwa razy więcej kulek niż w prawej.
Ile kulek było początkowo w każdej szufladzie?

RW3oPBWVSSDr3

Po lewej stronie grafiki znajduje się pomarańczowa ramka w kształcie prostokąta. Nad nią umieszczony jest nagłówek: "początkowo". W lewej części ramki umieszczone są zielone kulki w nieregularnym położeniu, a pod nimi znajduje się napis: "$x$". W prawej części ramki znajduje się więcej zielonych kulek. Pod kulkami znajduje się zapis: "$5x$". Po prawej stronie grafiki znajduje się niebieska ramka w kształcie prostokąta. Nad nią umieszczony jest nagłówek: "po przełożeniu kulek". W lewej części ramki umieszczone są zielone kulki w nieregularnym położeniu, a pod nimi znajduje się napis: "$x+18$". W prawej części ramki też znajdują się zielone kulki. Pod kulkami znajduje się zapis: "$5x-18$".

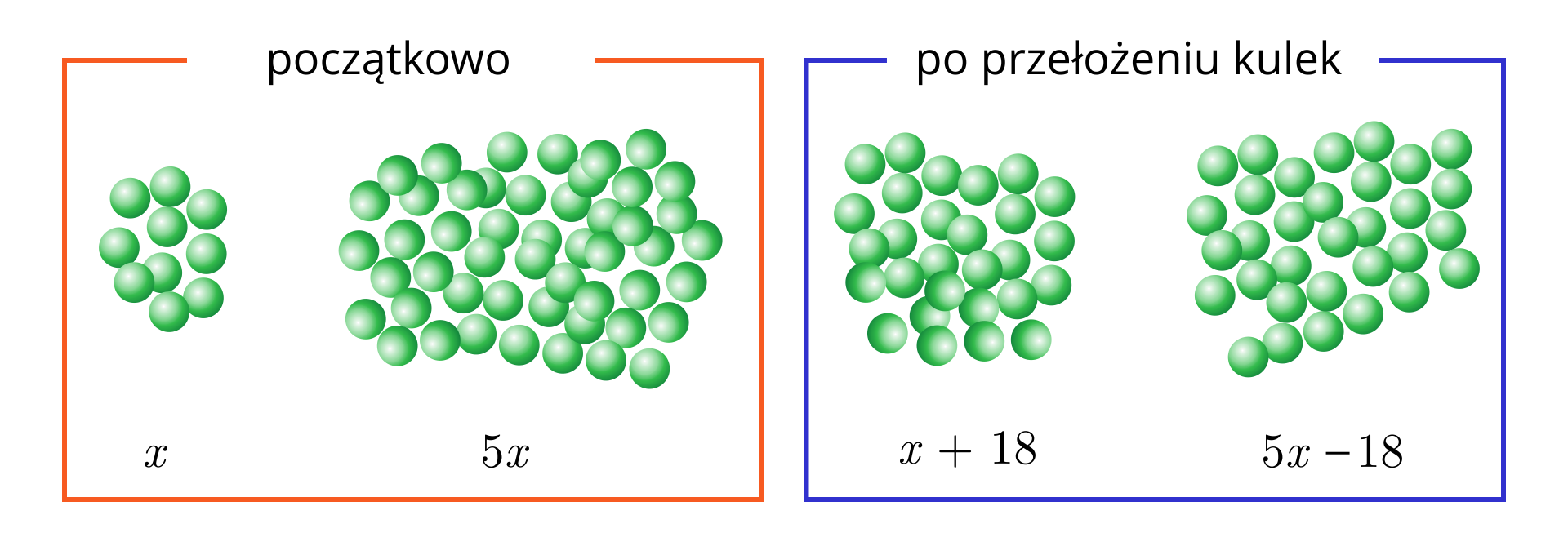
Analiza zadania:
$x$ – początkowa liczba kulek w lewej szufladzie, $x$ – liczba naturalna,
$5x$ – początkowa liczba kulek w prawej szufladzie,
$x+18$ – liczba kulek w lewej szufladzie po przełożeniu kulek,
$5x-18$ – liczba kulek w prawej szufladzie po przełożeniu kulek.
Układamy i rozwiązujemy równanie.

Wykonujemy mnożenie.

Do obu stron równania dodajemy $36-x$.

Redukujemy wyrazy podobne.

Dzielimy obie strony równania przez $9$.

Obliczamy, ile kulek było w prawej szufladzie.

Odpowiedź:
W prawej szufladzie było $30$ kulek, a w lewej $6$.

Zosia jechała rowerem dwie godziny, a następnie godzinę szła piechotą. W sumie przebyła $29 \mathrm{km}$. Z jaką średnią prędkością jechała rowerem, jeżeli piechotą szła z prędkością o $7 \frac{\mathrm{km}}{\mathrm{h}}$ mniejszą niż jechała rowerem?

R7bthz6BUpJ3E

Po lewej stronie grafiki umieszczone jest zdjęcie dziewczynki jadącej na rowerze po ulicy. Po prawej stronie ekranu znajduje się zdjęcie dziewczynki przechodzącej przez przejście dla pieszych. Pod fotografiami znajduje się pozioma przerywana linia w kolorze niebieskim. Jest ona podzielona pionową kreską na dwa odcinki stanowiące $\frac{2}{3}$ oraz $\frac{1}{3}$ długości. Dłuższy odcinek znajduje się pod dziewczynką jadącą na rowerze, natomiast krótszy pod spacerującą dziewczynką. Nad dłuższym odcinkiem znajduje się napis: "$2 \mathrm{h}$", natomiast nad krótszym: "$1 \mathrm{h}$". Pod fotografią dziewczynki na rowerze znajduje się zapis: "$\mathrm{x} \raisebox{1ex}{$\mathrm{km}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{h}$}\right.$", a pod fotografią dziewczynki na przejściu: "$\left(\mathrm{x}-7\right) \raisebox{1ex}{$\mathrm{km}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{h}$}\right.$". Obie ilustracje objęte są jedną wspólną klamrą, przy której znajduje się napis: "$29 \mathrm{km}$".

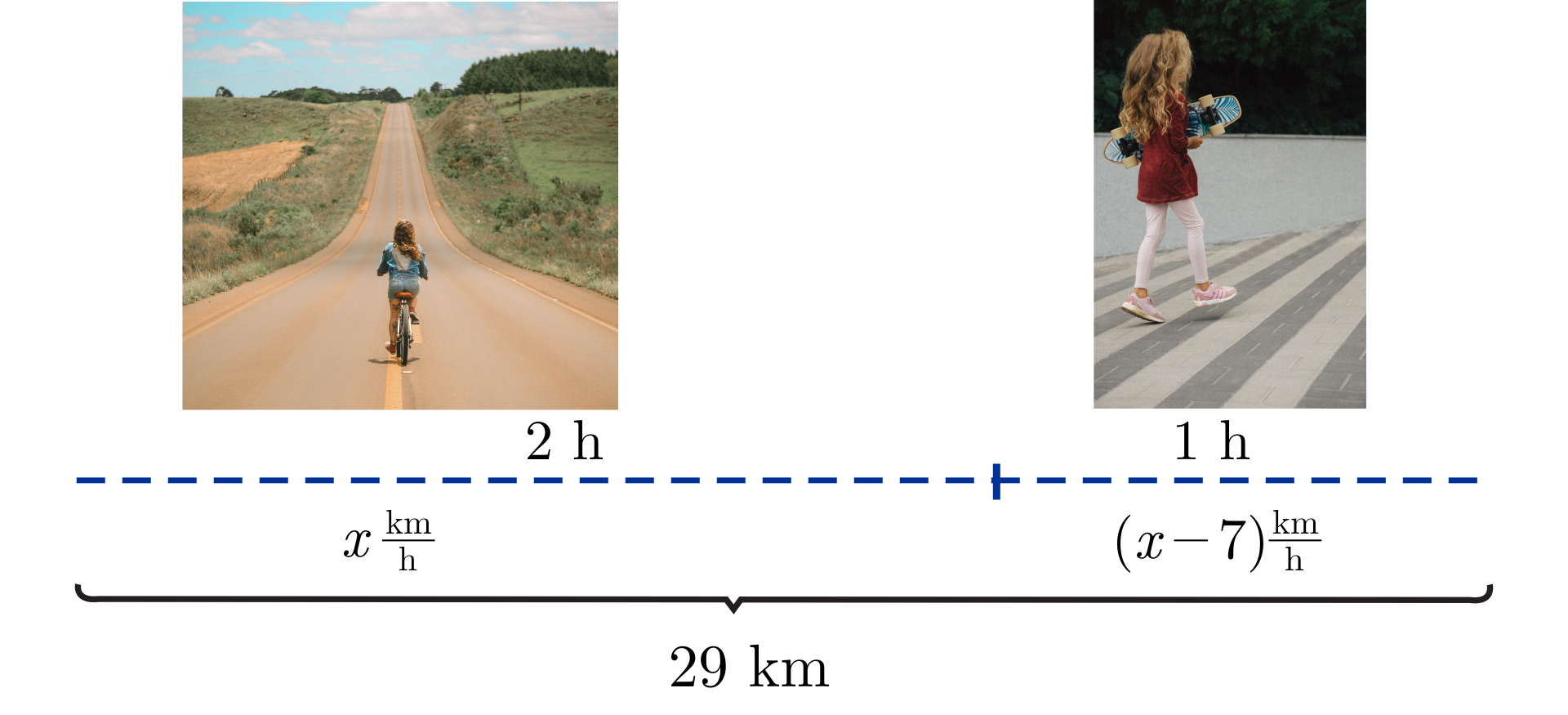
Analiza zadania:
$x$ – średnia prędkość, z jaką jechała Zosia rowerem (w $\frac{\mathrm{km}}{\mathrm{h}}$),
$x-7$ – średnia prędkość, z jaką szła Zosia (w $\frac{\mathrm{km}}{\mathrm{h}}$),
$2x$ – odległość, jaką przebyła Zosia rowerem (w $\mathrm{km}$),
$1·\left(x-7\right)$ – odległość, jaką Zosia przebyła piechotą (w $\mathrm{km}$).
Zapisujemy i rozwiązujemy równanie.

Wykonujemy mnożenie i redukujemy wyrazy podobne.

Do obu stron równania dodajemy $7$ i redukujemy wyrazy podobne.

Dzielimy obie strony równania przez $3$.

Odpowiedź:
Zosia jechała rowerem ze średnią prędkością $12 \frac{\mathrm{km}}{\mathrm{h}}$.

Wczoraj Ewa miała $\frac{1}{4}$ kwoty, którą miała Ela. Dzisiaj każda z dziewcząt dostała od rodziców po $10 \mathrm{zł}$ i teraz Ewa ma $\frac{2}{3}$ kwoty, którą ma Ela. Ile teraz pieniędzy ma każda z dziewcząt?

Układamy i rozwiązujemy równanie.

Mnożymy obie strony równania przez $12$, czyli najmniejszy wspólny mianownik ułamków $\frac{1}{4}$ i $\frac{2}{3}$.

Wykonujemy mnożenie i do obu stron równania dodajemy $\left(-3x-80\right)$

Redukujemy wyrazy podobne i dzielimy obie strony równania przez $5$.

Obliczamy, ile pieniędzy ma dzisiaj Ela.
$8+10=18 \left(\mathrm{zł}\right)$
Obliczamy, ile pieniędzy ma dzisiaj Ewa.
$\frac{1}{4}·8+10=2+10=12 \left(\mathrm{zł}\right)$

Odpowiedź:
Ela ma $18 \mathrm{zł}$, a Ewa ma $12 \mathrm{zł}$.

W prostokącie jeden bok jest o $6$ dłuższy od drugiego. Obwód prostokąta jest równy $32$.
Oblicz długości boków tego prostokąta.

R1KHyp67tVd6n

Ilustracja przedstawia prostokąt wypełniony kolorem niebieskim. Boki poziome są dłuższe od boków pionowych. Długość boków poziomych wynosi "$x+6$", natomiast boków pionowych "$\mathrm{x}$".

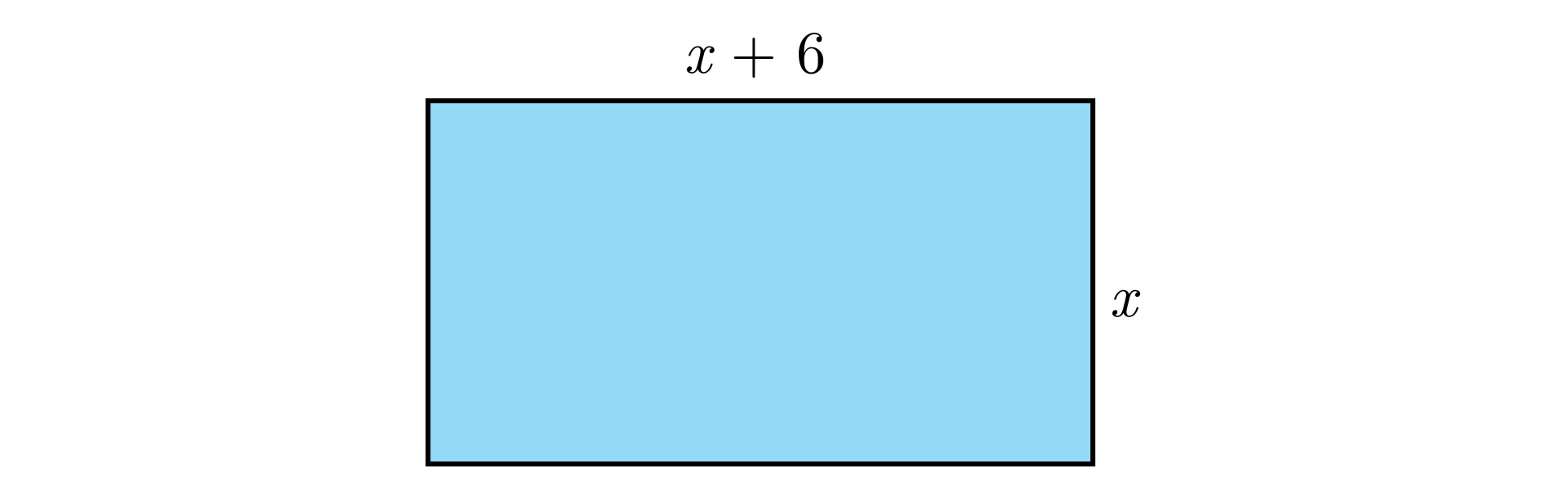
Analiza zadania:
$x$ – długość krótszego boku prostokąta,
$x+6$ – długość dłuższego boku prostokąta.
Układamy i rozwiązujemy odpowiednie równanie.

Dzielimy obie strony równania przez $2$.

Redukujemy wyrazy podobne i od obu stron równania odejmujemy $6$.

Redukujemy wyrazy podobne i dzielimy obie strony równania przez $2$.

Obliczamy długość dłuższego boku prostokąta.

Odpowiedź:
Długości boków prostokąta są równe $5$ i $11$.

metoda takiego przekształcania równania, aby po każdym przekształceniu otrzymać równanie równoważne danemu.