Skumulowany procentowy rozkład danych

Zapoznaj się z poleceniem poniżej.

Sprawdźmy teraz, jak procentowo będą się rozkładać dane narastające pokazane na filmie. Jak się zapewne domyślasz, formułę należy rozbudować w taki sposób, aby otrzymać udziały, które zostaną na koniec zamienione na procenty.

Pobierz plik z przykładowymi danymi umieszczony poniżej filmu.

W tym celu:

1. Wyczyść poprzednie wyniki z zakresu F4:F8.

2. Do komórki F4 wpisz następującą formułę:

=SUMA(JEŻELI($B$4:$B$18<=E4;1;0))/ILE.LICZB($B$4:$B$18)

3. Zatwierdź ją kombinacją klawiszy [Ctrl]+[Shift]+[Enter].

4. Skopiuj formułę w dół i otrzymanym wynikom nadaj format procentowy.

Wyjaśnienie działania formuły:

W pierwszym argumencie funkcji JEŻELI() każda wartość z zakresu B4:B18 porównywana jest z wartością graniczną w komórce E4. Jeśli jest mniejsza od niej bądź jej równa, wówczas zwracana jest wartość logiczna PRAWDA.

Jeżeli jest większa, wówczas wynikiem testu jest FAŁSZ. Dzięki temu, że formuła została zatwierdzona tablicowo, tworzona jest tablica wartości logicznych. Wartości PRAWDA są zamieniane na liczbę 1, a FAŁSZ na 0.

Te wartości są do siebie dodawane za pomocą funkcji SUMA(). Aby można było swobodnie stosować formułę dla kolejnych przedziałów, zastosowano odpowiednie adresowanie komórek.

Zakres danych źródłowych musi być zablokowany za pomocą bezwzględnego adresowania komórek ($), a komórka stanowiąca kryterium porównywania (E4) powinna mieć adresowanie względne. Dzięki temu kryterium automatycznie się dostosuje w miarę kopiowania formuły do kolejnych komórek.

Zwracane wyniki przez pierwszą część formuły dzielone są przez liczbę elementów liczbowych w analizowanym zakresie (B4:B18, tj. 15 wartości). Do jej wyznaczenia służy funkcja ILE.LICZB(). Wynikiem ilorazu są ułamki, które po zamianie na procenty określają odpowiednie udziały.

R1WS7gvieQ0jg

Nagranie filmowe dotyczące zagadnienia skumulowanego procentowego rozkładu danych.

Nagranie filmowe dotyczące zagadnienia skumulowanego procentowego rozkładu danych.

Film dostępny pod adresem /preview/resource/R1WS7gvieQ0jg

Nagranie filmowe dotyczące zagadnienia skumulowanego procentowego rozkładu danych.

Pobierz przykładowe dane:

Polecenie 1

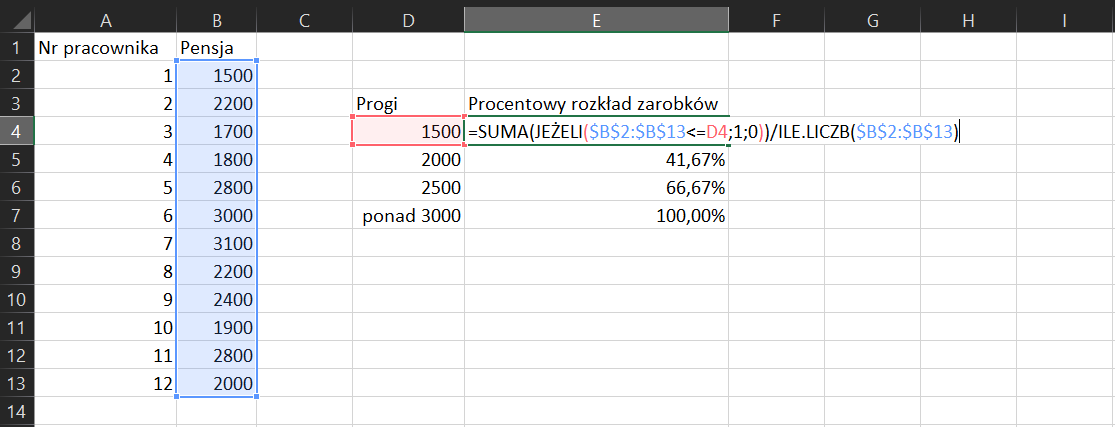
Rodzic prosi cię o pomoc w firmie. Chce się dowiedzieć, jaki procent jego pracowników otrzymuje pensję w określonym przedziale wartości. Utwórz arkusz, w którym w pierwszej kolumnie wpiszesz numer identyfikacyjny pracownika, a w drugiej jego pensję. Następnie stwórz tabelę pomocniczą, w której znajdą się wartości graniczne przedziałów pensji pracowników. Korzystając z poznanej funkcji, wykonaj potrzebne obliczenia.

Pokaż rozwiązanie

Przykładowe rozwiązanie zadania:

RJkOMEQT2JBaI

Na zrzucie ekranu widoczny jest fragment arkusza Excel. W komórce A1 wpisano tytuł numer pracownika. W komórce B1 wpisano tytuł pensja. W kolumnie A, w komórkach od A2 do A13, wprowadzono numer pracownika. W kolumnie B, w komórkach od B2 do B13, są wartości zarobków. W komórce D3 wpisano tytuł Progi. W komórkach od D4 do D7 wpisano wartości progów. W komórce E3 wpisano Procentowy rozkład zarobków. W komórce E4 wpisano formułę =SUMA(JEŻELI($B$2:$B$13<=D4;1;0))/ILE.LICZB($B$2:$B$13). W komórkach od E5 do E7 wpisano procenty.

Polecenie 2

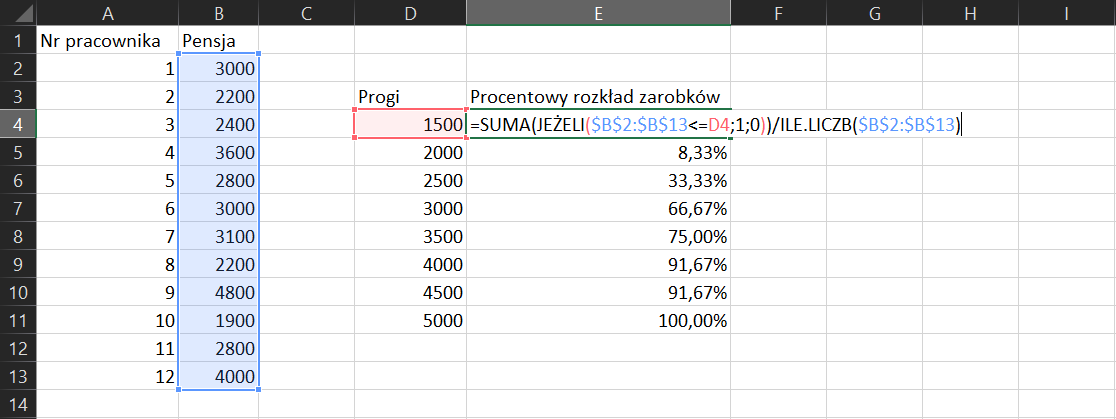
Niektórzy pracownicy w firmie twoich rodziców dostali awans i teraz zarabiają 2 razy więcej. Sprawdź, jak zmienił się procentowy rozkładskumulowany procentowy rozkładprocentowy rozkład zarobków.

Pokaż rozwiązanie

Przykładowe rozwiązanie zadania:

RyWqr3BdvK6iJ

Na zrzucie ekranu widoczny jest fragment arkusza Excel. W komórce A1 wpisano tytuł numer pracownika. W komórce B1 wpisano tytuł pensja. W kolumnie A, w komórkach od A2 do A13, wprowadzono numer pracownika. W kolumnie B, w komórkach od B2 do B13, są wartości zarobków. W komórce D3 wpisano tytuł Progi. W komórkach od D4 do D11 wpisano wartości progów. W komórce E3 wpisano Procentowy rozkład zarobków. W komórce E4 wpisano formułę =SUMA(JEŻELI($B$2:$B$13<=D4;1;0))/ILE.LICZB($B$2:$B$13). W komórkach od E5 do E11 wpisano procenty.

Słownik