Schemat interaktywny
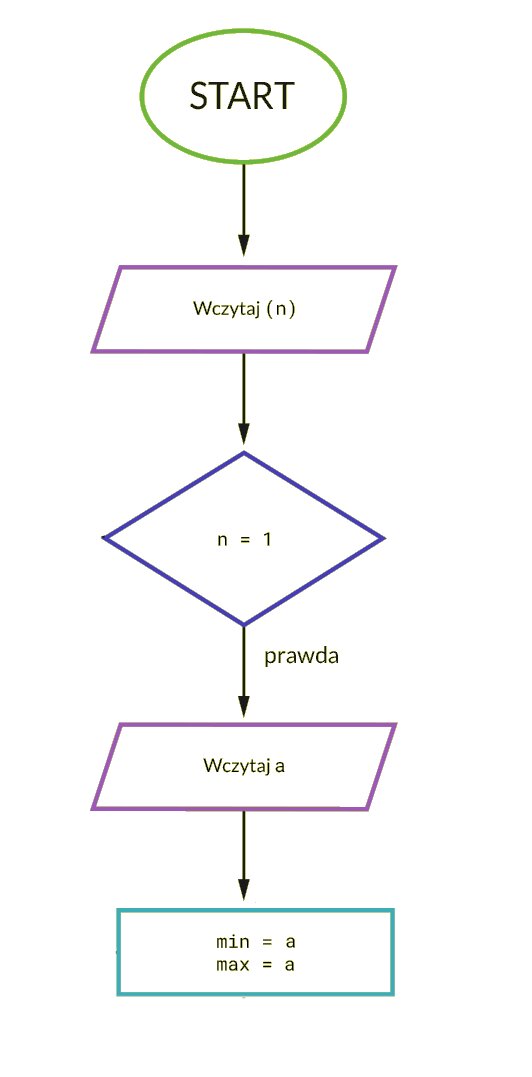
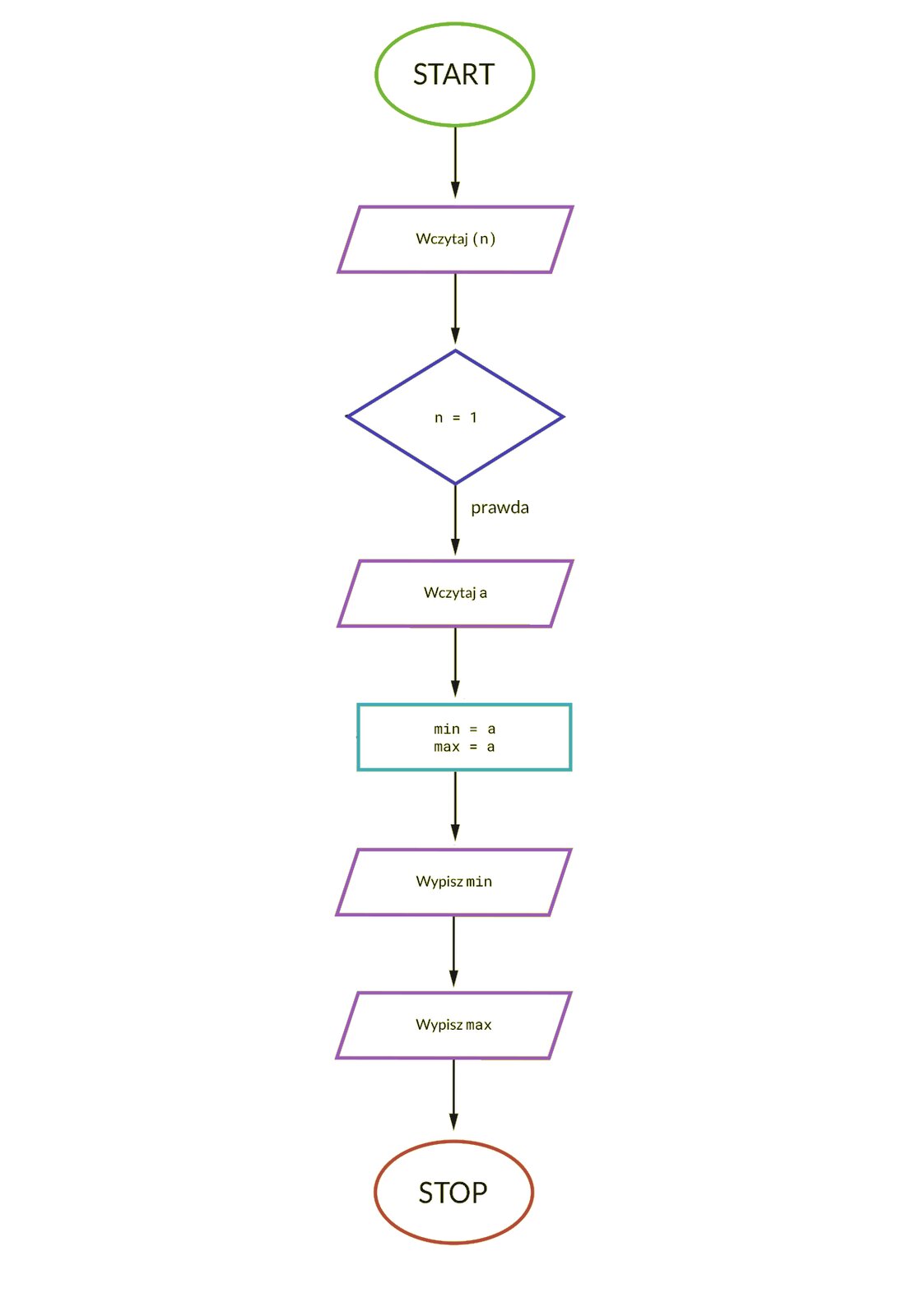
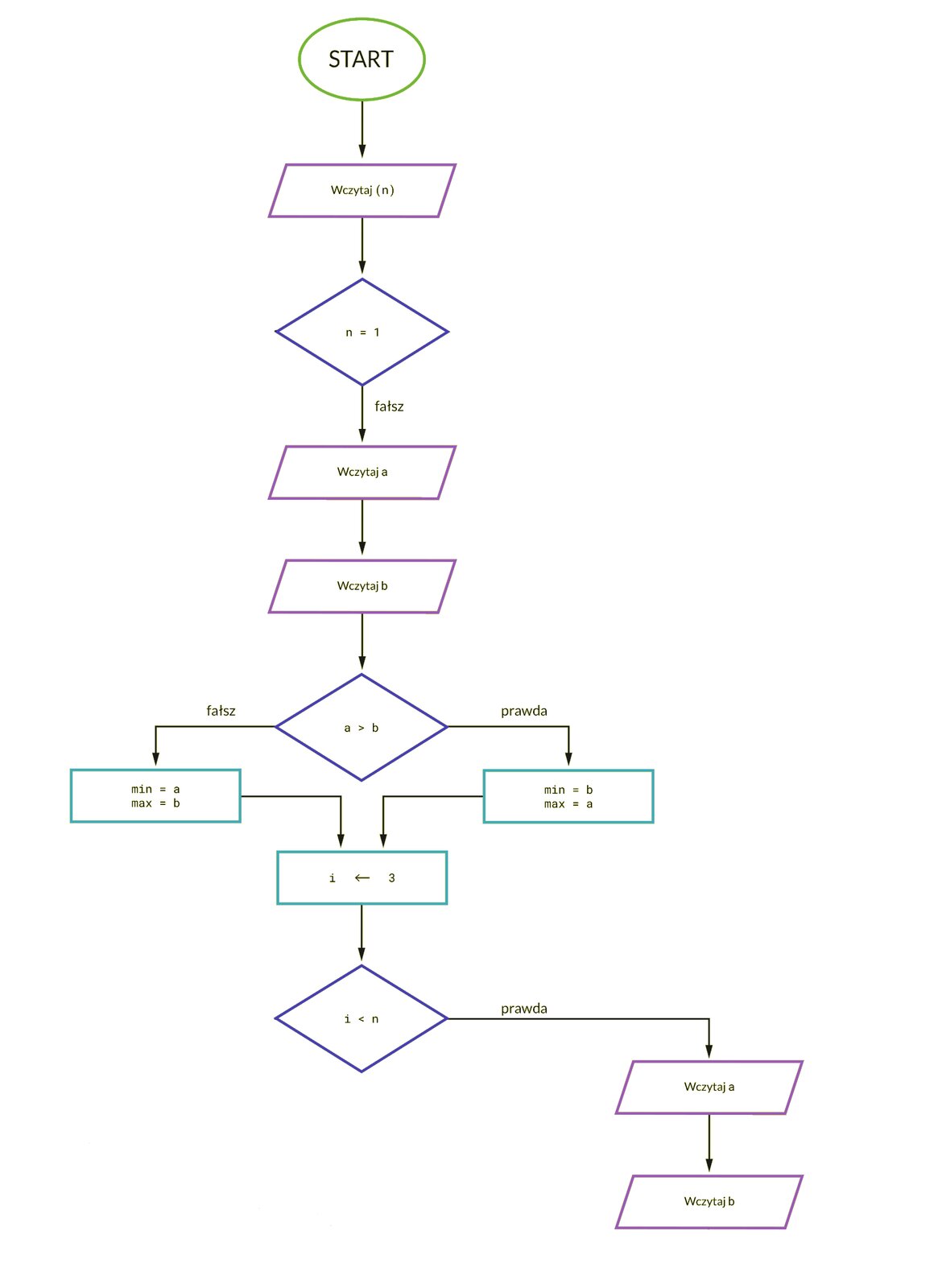
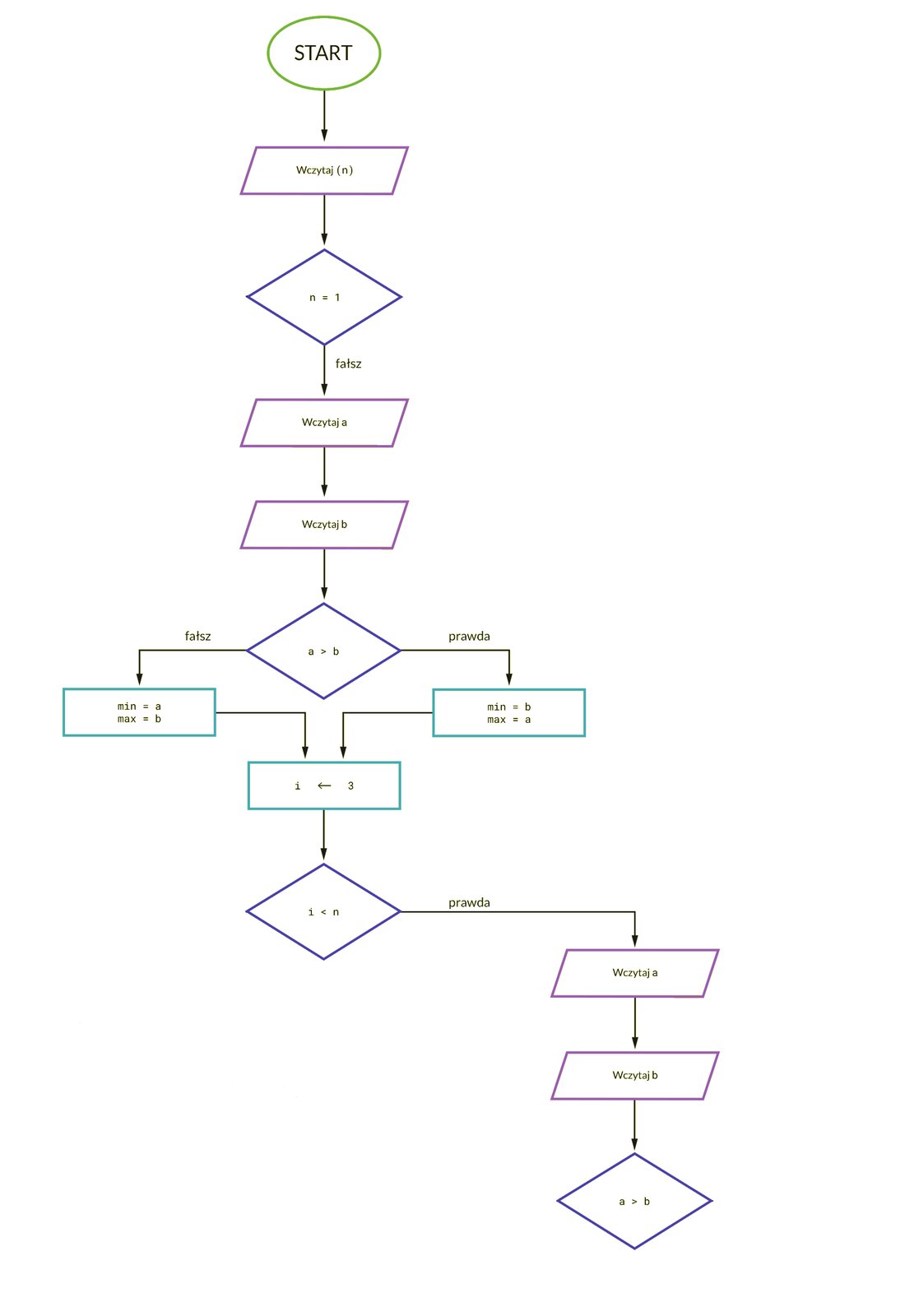
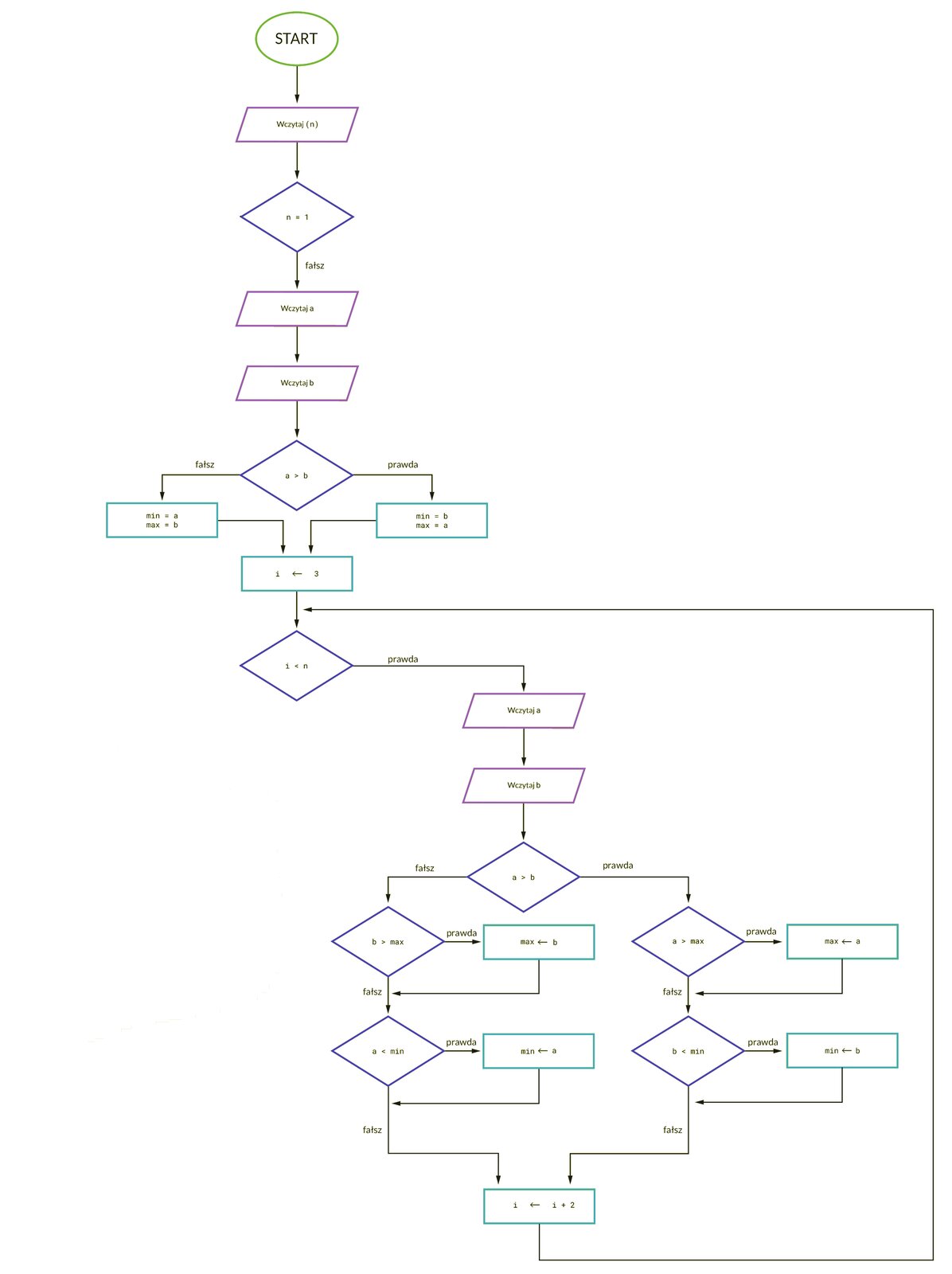
Napisz algorytm, który w zbiorze liczb podanych przez użytkownika znajdzie jednocześnie liczbę największą i najmniejszą. Instrukcji warunkowej użyjemy podczas porównywania wartości między sobą.
Do rozwiązania tego problemu użyjemy algorytmu znajdowania jednocześnie minimum i maksimum, używającego najmniejszej liczby porównań.
W algorytmie znajdowania obu wartości: minimum oraz maksimum w zbiorze potrzebujemy porównań. Dzięki zastosowaniu algorytmu do jednoczesnego znajdowania wartości minimalnej i maksymalnej możemy znacząco ograniczyć liczbę porównań do: dla parzystej liczby elementów oraz do dla nieparzystej.
Specyfikacja:
Dane:
n– liczba elementów w tablicy; liczba naturalna dodatnia;liczb wprowadzonych przez użytkownika; zbiór liczb całkowitych.
Wynik:
min– najmniejsza liczba w zbiorze liczb wprowadzonych przez użytkownika; liczba całkowita;max– największa liczba w zbiorze liczb wprowadzonych przez użytkownika; liczba całkowita.
Pisanie algorytmu rozpoczynamy od bloku START. Pobieramy do zmiennej n liczbę liczb, które wprowadzi użytkownik.
Sprawdzamy, czy dany zbiór liczb posiada jeden element. Jeżeli tak, to wczytujemy jedyną liczbę a od użytkownika, która będzie jednocześnie szukanym minimum oraz maksimum. Przypisujemy jej wartość do zmiennych min oraz max.
W tym najprostszym przypadku możemy wypisać znalezioną wartość minimalną oraz maksymalną, a następnie zakończyć algorytm blokiem STOP.
Przejdźmy teraz do tej bardziej wymagającej części naszego algorytmu. W przypadku, w którym mamy więcej niż jedną liczbę, wczytujemy od użytkownika pierwsze dwie liczby zbioru: a oraz b, które porównamy ze sobą za pomocą instrukcji warunkowej. W zależności do tego, która będzie mniejsza lub większa, przypiszemy je kolejno do wartości min oraz max — naszych potencjalnych kandydatów — na minimum oraz maksimum. Dla czytelności na rysunku pominięto przypadek, w którym warunek n = 1 jest prawdziwy — wrócimy do niego na końcu.
Tworzymy zmienną i, która pozwoli nam powtórzyć wczytywanie kolejnych liczb i umożliwi późniejsze przetworzenie ich, czyli odpowiada za sterowanie pętlą. Będzie ona przechowywała informację, którą z kolei liczbę musimy wczytać, dlatego jej początkowa wartość będzie wynosiła 3 (ponieważ dwie pierwsze liczby zostały już wczytane).
Definiujemy teraz warunek, dzięki któremu będziemy mieli pewność, że wczytaliśmy tyle liczb, ile zamierzaliśmy. Sprawia on, że pętla będzie się wykonywać, dopóki wartość zmiennej i będzie mniejsza od n.
Pierwszą czynnością podczas każdego wykonania pętli będzie wczytanie od użytkownika dwóch kolejnych wartości liczbowych, które następnie zapisujemy w zmiennych a oraz b.
Następnie porównujemy ze sobą wczytane liczby a oraz b. Dzięki informacji, która z tych liczb jest mniejsza/większa, będziemy mogli zaoszczędzić dużo porównań, ponieważ nie będziemy musieli każdej z nich porównywać z obecnymi kandydatami na minimum oraz maksimum.
Na początku spróbujemy znaleźć nowe maksimum. W tym celu sprawdzamy, czy wprowadzona wartość a jest większa od dotychczas znalezionego maksimum, czyli wartości zmiennej max. Jeżeli sprawdzona liczba jest większa, to staje się nowym maksimum.
Podobnie postępujemy z liczbą b. Sprawdzamy, czy jej wartość jest mniejsza od dotychczas znalezionego minimum, zapisanego w zmiennej min. Jeżeli tak, to sprawdzana liczba staje się nowym minimum.
Analogiczna sytuacja zachodzi w przypadku gdy nie zachodzi warunek a > b. Daje nam to informacje, że a nie będzie szukanym maksimum, a b minimum.
Sprawdzamy kandydata na maksimum, liczbę b, czy jest większa od dotychczas znalezionego maksimum. Jeżeli tak, to aktualizujemy zmienną max. Podobnie sprawdzamy nowego kandydata na minimum, liczbę a, czy jest mniejsza od dotychczas znalezionego minimum. Jeżeli tak, to aktualizujemy zmienną min.
W obu przypadkach na końcu zwiększamy zmienną i o 2, ponieważ przetworzyliśmy dwie liczby (a oraz b). Następnie ponownie sprawdzamy warunek pętli. Dzięki temu pętla się zakończy, gdy wartość zmiennej i osiągnie wartość równą lub większą od n.
Pozostaje nam przeanalizować, co się dzieje po wyjściu z pętli. Z racji tego, że zawsze przetwarzaliśmy po dwie liczby, wczytaliśmy parzystą liczbę liczb. W przypadku, gdy n jest nieparzyste, pozostaje nam rozpatrzyć ostatnią liczbę osobno. W takiej sytuacji wartość zmiennej i będzie równa n (w przeciwnym i wypadku byłoby większe).
Wczytujemy wprowadzoną liczbę i zapisujemy ją do zmiennej a.
Ostatnia wczytana liczba może być zarówno szukanym minimum jak i maksimum, ponieważ nie została jeszcze porównana z żadną inną liczbą. W związku z tym musimy porównać ją zarówno z obecnym minimum, jak i maksimum. Jeżeli wykryjemy, że wczytana liczba jest mniejsza od minimum lub większa od maksimum, to aktualizujemy zmienne odpowiednio min oraz max, przypisując im wartość rozpatrywanej liczby.
Po rozpatrzeniu przypadku, w którym posiadamy nieparzystą liczbę liczb, przetworzyliśmy już wszystkie liczby podane przez użytkownika. Możemy teraz wypisać znalezione minimum oraz maksimum, tak samo, jak było to w przypadku gdy zbiór wejściowy posiadał jeden element. Powyżej przedstawiono końcową wersję algorytmu.
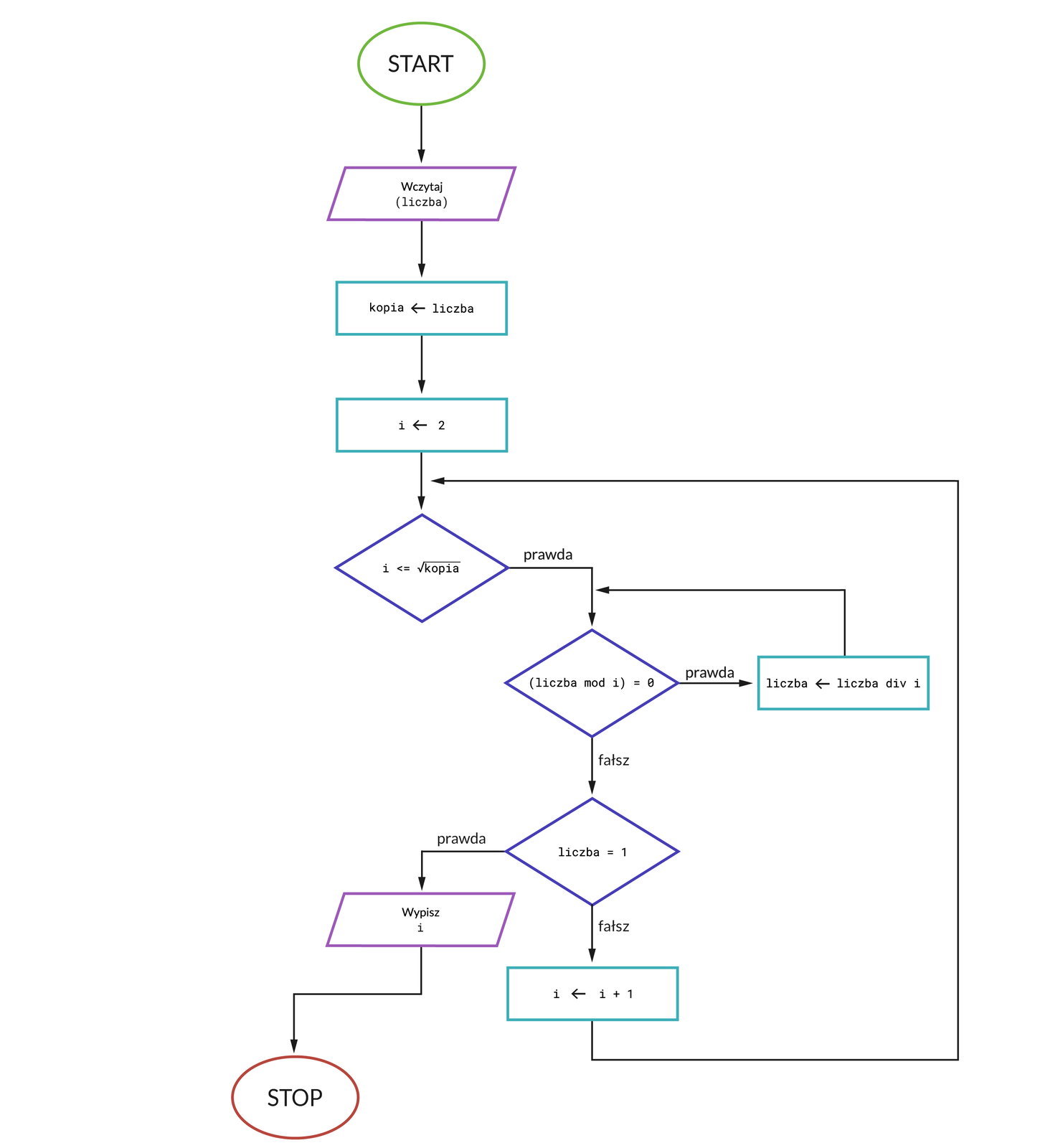
Zaprojektujmy algorytm do sprawdzania stopnia K‑gładkości danej liczby liczba.
Liczba naturalna jest K‑gładka, jeżeli wszystkie dzielniki pierwsze są nie większe niż K. W celu określenia stopnia K‑gładkości liczby, musimy rozłożyć ją na czynniki pierwsze, a następnie określić, który z tych czynników jest największy.
Przykłady:
– jej stopień K‑gładkości wynosi (największy dzielnik pierwszy);
– jest to liczba pierwsza, dlatego jej stopień K‑gładkości wynosi tyle ile jej wartość, czyli ;
– stopień K‑gładkości wynosi .
Specyfikacja:
Dane:
liczba– liczba naturalna
Wynik:
Program wypisuje K-liczba, stopień K‑gładkości liczby.
Pisanie algorytmu rozpoczynamy od bloku START. Do rozwiązania tego zadania wykorzystamy algorytm rozkładu liczby na czynniki pierwsze. Do zmiennej liczba pobieramy wartość podaną przez użytkownika, dla której będziemy chcieli określić jej stopień K‑gładkości.
Zapisujemy kopię wczytanej liczby do zmiennej kopia. Robimy tak, ponieważ będziemy modyfikować wartość wczytanej liczby, a będzie nam potrzebna również jej pierwotna wartość – w celu ustalenia warunku końca pętli.
W następnym kroku tworzymy zmienną i, która pozwoli sprawdzać, czy kolejne liczby są dzielnikami zadanej liczby (odpowiada za sterowanie pętlą). Jej początkowa wartość będzie wynosiła 2, ponieważ jest to najmniejsza liczba pierwsza.
Następnie potrzebna będzie pętla. Za jej pomocą będziemy szukać – w kolejności rosnącej – wszystkich kolejnych dzielników wczytanej liczby, w celu określenia największego z nich. Ustawiamy warunek pętli, która będzie powtarzana, dopóki wartość zmiennej i będzie nie większa niż pierwiastek z wartości wczytanej liczby (). Sprawdzanie warunku dla wyższych wartości nie ma sensu z powodu właściwości liczb pierwszych – powyżej tej wartości nie znajdziemy już więcej dzielników.
Następnie sprawdzamy, czy nasza liczba jest podzielna przez wartość zmiennej i. Jeżeli tak, to dzielimy ją przez wartość i. Powtarzamy dzielenie dopóty, dopóki nasza liczba nie osiągnie wartości niepodzielnej przez i.
Następnym krokiem będzie sprawdzenie, czy wartość liczby będzie wynosiła jeden. Jeżeli tak, to oznacza, że zakończyliśmy rozkład tej liczby na czynniki pierwsze, a największym czynnikiem rozkładu, czyli stopniem K‑gładkości, jest liczba i (nie ma już większych czynników, ponieważ obecny był ostatnim). W takim przypadku, z racji tego, że jest to szukana wartość, możemy ją wypisać i zakończyć działanie algorytmu blokiem STOP.
W przeciwnym wypadku (gdy wartość liczby będzie wciąż większa od jeden) musimy powtórzyć krok dla kolejnego potencjalnego dzielnika. W tym celu zwiększamy wartość zmiennej pomocniczej i o jeden i wracamy do sprawdzenia warunku pętli, czyli tego, czy zmienna i jest mniejsza od pierwiastka wartości zmiennej kopia lub jej równa.
Pozostał ostatni fragment naszego algorytmu. Musimy określić, co się stanie, gdy przestanie zachodzić warunek pętli i gdy nie znajdziemy rozwiązania w trakcie jej wykonywania. W takim wypadku wiemy, że podana liczba jest liczbą pierwszą, ponieważ w zakresie nie znaleźliśmy żadnego jej dzielnika. Z racji tego, że określiliśmy, że jest to liczba pierwsza, wiemy, że jej największym dzielnikiem pierwszym, czyli stopniem K‑gładkości, jest ona sama. Wypisujemy wartość kopii liczby i kończymy działanie algorytmu, idąc do etykiety STOP.
Przygotuj algorytm, który losuje trzy liczby naturalne dodatnie z zakresu od 1 do 100 włącznie – wiek trzech osób, a następnie wyznacza najstarszą osobę (jeżeli osoby będą w tym samym wieku, wybierz pierwszą z nich).
Napisz program w języku Python, który losuje trzy liczby naturalne dodatnie z zakresu od 1 do 100 włącznie – wiek trzech osób, a następnie wyznacza najstarszą osobę (jeżeli osoby będą w tym samym wieku, wybierz pierwszą z nich).
Specyfikacja:
Dane:
osoba1– wylosowany wiek pierwszej osoby; liczba naturalna z zakresu ;osoba2– wylosowany wiek drugiej osoby; liczba naturalna z zakresu ;osoba3– wylosowany wiek trzeciej osoby; liczba naturalna z zakresu ;
Wynik:
Program najpierw wyświetla wiek każdej osoby, a następnie podaje, która z osób jest najstarsza.