Skale Wszechświata

Duży, a nawet astronomicznie ogromny – takie określenia pasują do WszechświataWszechświatWszechświata. Składa się on jednak z małych drobin – elektronów, atomów. Ile ich znajduje się w całym Wszechświecie? Wszystko co jest wokół nas, świat mikro i makroskopowy, obserwować możemy w różnych skalach. Jakie wielkości są małe a jakie duże? Przekonajmy się.

Przeczytaj

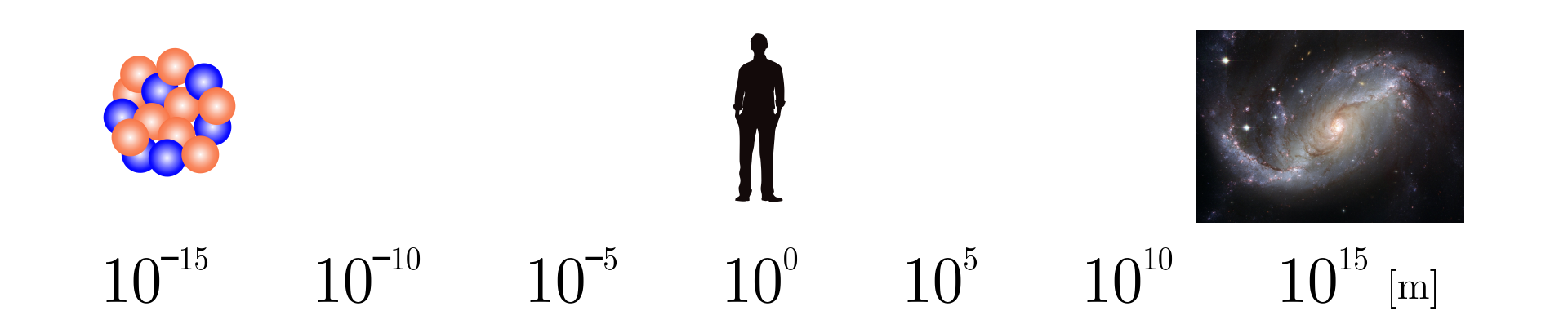
W trakcie powstawania Wszechświata, wolne atomy składały się na pierwsze gwiazdy i planety. Łączyły się w cząsteczki i minerały, a później też, przynajmniej w przypadku Ziemi, w związki organiczne, z których powstało życie. Wszystko wokół składa się z atomów. Jak dobrze wiemy są one niewielkie, masa protonów to zaledwie ${10}^{-27} \mathrm{kg}$. W całym Wszechświecie jest ich zatem niewyobrażalnie dużo. Wszechświat ma średnicę około $88\cdot {10}^{25} \mathrm{m}$ (czyli $880000000000000000000000000 \mathrm{m}$), średnica Ziemi to niecałe $13000 \mathrm{km}$ ($13000000 \mathrm{m}$), a rozmiary atomów są rzędu ${10}^{-10} \mathrm{m}$ ($0,000000001 \mathrm{m}$).

RBeqbwlQU8rNx

Na ilustracji skala od dziesięć do potęgi minus piętnastej do dziesięć do potęgi piętnastej, co dziesięć do piątej metra. Nad najmniejszą liczbą znajduje się ilustracja jądra atomu. Składa się ono z niebieskich i czerwonych kulek. Nad środkiem skali, w okolicy dziesięć do potęgi zero metra, sylwetka człowieka. Nad największą liczbą zdjęcie galaktyki.

Aby mówić o całym Wszechświecie i jego składowych posługując się znanymi jednostkami – np. metrami jako jednostkami odległości, czy kilogramami jako jednostkami masy – musimy stosować ich wielokrotności i podwielokrotności. Nie sposób ogarnąć całej makroskali kosmosu i mikroskali cząstek jednostką główną. Najpopularniejsze wielokrotności i podwielokrotności nie rozwiązują jednak sprawy. Zwykle poruszamy się w granicach od ${10}^{-6}$ do ${10}^6$, wyższe znamy bardziej jako wielokrotności pamięci komputerowych – terabajty, gigabajty.

Inną opcją na wyrażenie zarówno małych jak i dużych wielkości jest zastosowanie skali. Skala informuje nas ile razy dane wymiary (np. odległość, masa) są mniejsze lub większe od przyjętego wzorca. Na mapach zwykle odnosimy się do $1 \mathrm{cm}$, np. skala $1:50000$ oznacza, że $1 \mathrm{cm}$ na mapie odpowiada $50000 \mathrm{cm}$ (czyli $500 \mathrm{m}$) w rzeczywistości. W przypadku rozmiarów Wszechświata musielibyśmy zastosować bardzo dużą skalę. Odległość między Ziemią a Słońcem to około $150$ milionów kilometrów, czyli $15000000000000 \mathrm{cm}$. Zatem mapa w skali $1:50000$ musiałaby mieć długość przynajmniej $3000 \mathrm{km}$, aby móc pokazać odległość między Ziemią a Słońcem.

Zastosowanie skali także nie do końca rozwiązuje wyrażanie małych jak i dużych wielkości, dlatego poza stosowaniem wielokrotności i podwielokrotności skali jako porównań, stosuje się też specjalne jednostki.

Rozmiary Wszechświata są tak ogromne, że często trudno je wyrazić. Nawet odległości między planetami a Słońcem są tak dużymi liczbami, jakich zwykle się nie używa. Dla przykładu:

• odległość między Ziemią a Księżycem wynosi prawie $400000000 \mathrm{m}$,

• najbliższa planeta, Mars, jest odległa od Ziemi średnio o $225000000000 \mathrm{m}$,

• odległość między Ziemią a Słońcem to prawie $150000000000 \mathrm{m}$.

Jak widać, odległości w astronomii są duże, więc zwykle nie podaje się ich w metrach. Posługujemy się specjalnymi jednostkami, między innymi latami świetlnymi (light year [lajt jer] – $\mathrm{ly}$). Jeden rok świetlny określa odległość jaką światło przebywa w ciągu roku i jest to $9,46·{10}^{15} \mathrm{m}$. Inne to np. jednostka astronomiczna (astronomical unit [astronomikal junit] – $\mathrm{au}$) lub parsek (parsec [parsek] – $\mathrm{pc}$). $1 \mathrm{au}$ wynosi w przybliżeniu $150$ milionów kilometrów, a parsek to $3,086·{10}^{16} \mathrm{m}$.

Z drugiej strony mamy małe wielkości mikroskali. Przy wielkościach atomów stosuje się zwykle podwielokrotności, np. promień atomu wodoru wynosi $53 \mathrm{pm}$ (pikometry), czyli $0,53·{10}^{-10} \mathrm{m}$. Tutaj także pojawia się jednostka specjalna – jest to angstrem, $1 \mathrm{\AA }$ to dokładnie ${10}^{-10} \mathrm{m}$. Używa się go głównie do wyrażania odległości w skali atomowej, np. promieni atomów albo długości wiązań w cząsteczkach. Poza angstremem znana jest jeszcze długość Plancka – wielkość określona przez Maxa Plancka [maks plank]. Wynosi ona $1,616·{10}^{-35} \mathrm{m}$. Jest to wielkość mniejsza od protonu czy elektronu, a nawet od kwarków.

Jak najłatwiej zrozumieć makro i mikroskalę Wszechświata? Z pomocą przychodzi tutaj projekt dostępny na stronie https://htwins.net/scale2/ stworzony przez dwóch braci (wówczas $14$–latków) z Kalifornii. Pomysłodawcą był jeden z nich – Cary Huang [kery huan]. Na stronie możemy, przesuwając suwakiem, przemieszczać się od rozmiaru całego Wszechświata, przez gwiazdy, planety, państwa, znane obiekty architektoniczne, rozmiary zwierząt, owadów, mikroorganizmów, aż do atomów, cząstek i długości Plancka. Poruszamy się tam od odległości rzędu ${10}^{27} \mathrm{m}$ do ${10}^{-35} \mathrm{m}$, dzięki czemu możemy zauważyć ogrom skali Wszechświata.

Skale Wszechświata

Sprawdź się

Słownik

Bibliografia

Encyklopedia PWN

Sagnowska B., Szot‑Gawlik D., Godlewska M., Rozenbajgier M., Rozenbajgier R., 2017, Świat fizyki, Warszawa, WSiP