Spadanie swobodne jako przykład zmiany energii potencjalnej w kinetyczną

Materiał ten jest wzbogaceniem do Ruch jednostajnie przyspieszony prostoliniowyPZaibPYnDRuch jednostajnie przyspieszony prostoliniowy.

Jak wiesz, ruch jest wszędzie. Poznałeś zapewne kilka jego rodzajów. Fizycy bardzo chętnie badają i wyznaczają różne parametry ruchu. Dzisiaj zajmiemy się jego szczególnym przypadkiem, w którym ciała poruszają się tylko pod wpływem siły grawitacji. W czasie takiego ruchu dochodzi do zmian w energii mechanicznej. Przedstawimy więc, jak opisać taki ruch na podstawie zasady zachowania energii mechanicznejzasada zachowania energii mechanicznejzasady zachowania energii mechanicznej. Zapraszam Cię do zapoznania się z tym materiałem.

Ze spadkiem swobodnym, spotykamy się podczas ruchu tylko pod wpływem siły grawitacji. Przykładem może być ruch planet wokół Słońca czy Księżyca wokół Ziemi, lot kosmiczny, gdy statek porusza się z wyłączonymi silnikami, czy wreszcie, bliżej nas, spadanie ciał w pobliżu powierzchni Ziemi.

R11AHNodEdXgy

Statek kosmiczny przemieszczający się w kosmosie na czarnym tle z widocznym w dolnej części ilustracji fragmentem Ziemi. Na module dowodzenia flaga amerykańska. Dolna część statku posiada stateczniki.

Oczywiście, w analizowanych tu przypadkach będziemy mówili o warunkach idealnych, czyli takich, z którymi nie spotykamy się na co dzień. W powietrzu oprócz siły grawitacji na ciało działa opór powietrza. Jednak jeśli wartość siły oporu jest dostatecznie mała i nie wpłynie znacząco na wyniki badań, to taki ruch możemy traktować jako spadek swobodny. Zdając sobie sprawę z takich sposobów przybliżenia, możemy z dość dużą dokładnością opisać spadek swobodny ciał w naszym otoczeniu, gdy te warunki nie są laboratoryjne.

Spadek swobodny jest przykładem ruchu jednostajnie przyspieszonego prostoliniowego, z przyspieszeniem $g$ równym przyspieszeniu grawitacyjnemu.

R3b7nG66bceEH

Na grafice umieszczono jabłko. Od środka jabłka w dół odchodzi wektor. Z prawej strony wektora wzór na siłę ciężkości: duże ef równa się małe em razy małe gie.

Energia mechaniczna ciała jest sumą jego energii kinetycznej i potencjalnej:

gdzie:
$E_{\mathrm{m}}$ – energia mechaniczna,
$E_{\mathrm{k}}$ – energia kinetyczna,
$E_{\mathrm{p}}$ – energia potencjalna.

Energia kinetyczna związana jest z ruchem, natomiast energia potencjalna grawitacji z wysokością, na jakiej znajduje się ciało.

R1Mau4vYqjlWu

Grafika składa się z dwóch zdjęć umieszczonych obok siebie. Na zdjęciu z lewej widok trzech rowerzystów jadących po drodze na wzniesieniu, w oddali widok miasta. Na zdjęciu po prawej stronie pięciu robotników budowlanych siedzących na na metalowej belce umieszczonej wysoko nad ziemią. W tle poniżej szczyty wieżowców. Nad pierwszym zdjęciem ruch - energia kinetyczna plus nad zdjęciem po prawej stronie wysokość - energia potencjalna grawitacji. Na samej górze napis energia mechaniczna.

Energię kinetyczną wyrażamy wzorem:

Jak łatwo zauważyć, energia ta związana jest z masą ciała $m$ oraz jego prędkością $v$ (wszystkie ciała będące w ruchu posiadają prędkość, a więc we wzorze na energię kinetyczną nie mogło zabraknąć tej wielkości fizycznej).

Energię potencjalną grawitacji wyrażamy wzorem:

Tym razem zauważmy, że energia ta związana jest z wysokością nad pewnym obranym poziomem, który będziemy nazywali poziomem zerowym. Stąd, we wzorze pomnożymy masę $m$, przyspieszenie grawitacyjne $g$ oraz wysokość $h$.

Zasada zachowania energii mechanicznej mówi, że w określonych warunkach całkowita energia mechaniczna nie ulega zmianie:

Oznacza to, że suma energii potencjalnej i kinetycznej powinna mieć tę samą wartość.

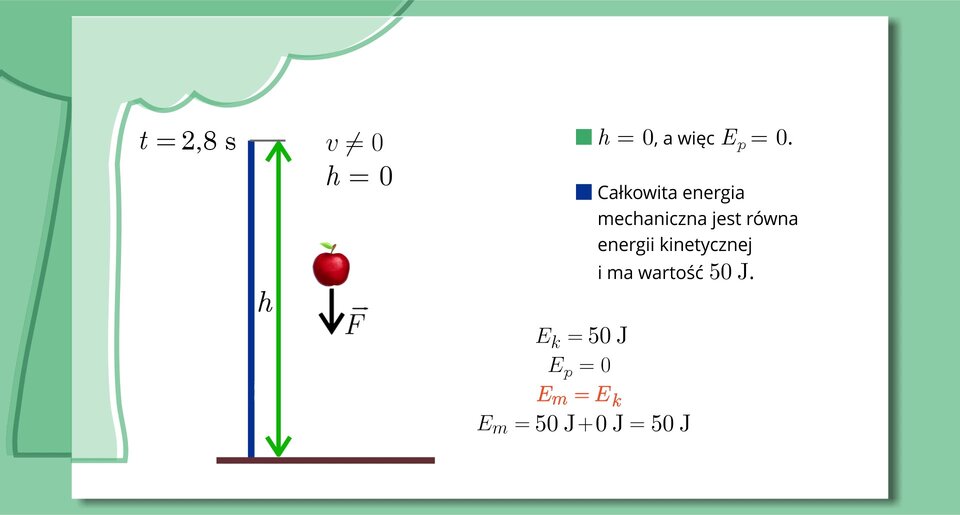
Samolot posiada energię mechaniczną o wartości $80 \mathrm{J}$. Jeśli na to ciało nie będzie działała siła tarcia lub oporu powietrza (lub siły te będą miały małą wartość taką, że będziemy mogli je zaniedbać), ani żadne siły zewnętrzne nie będą wykonywały nad nim pracy, wówczas, zgodnie z zasadą zachowania energii, wartość ta nie ulegnie zmianie.

Jeśli samolot będzie leciał niżej, wówczas jego energia potencjalna zmniejszy się, a więc wzrośnie wartość energii kinetycznej.

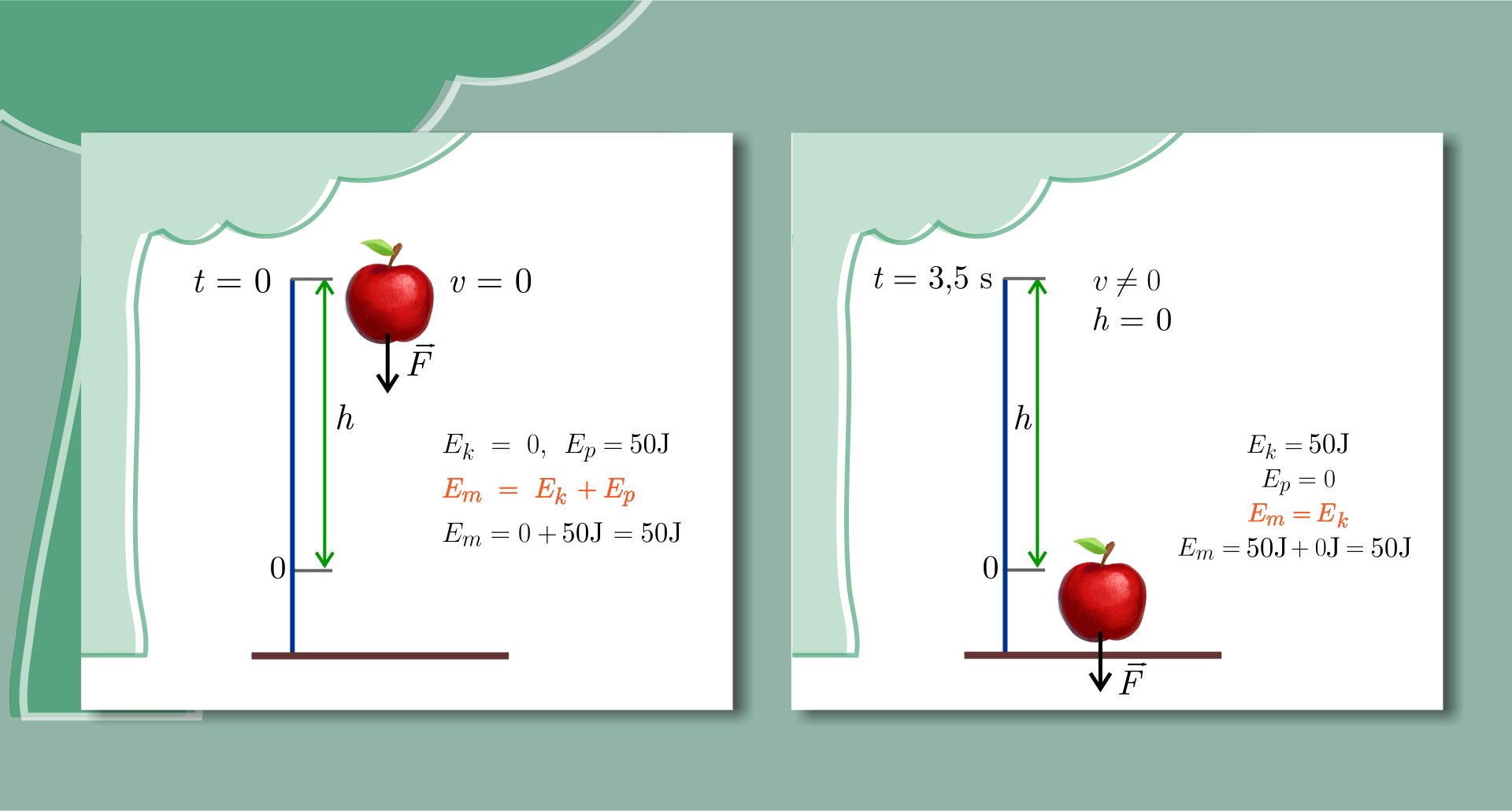
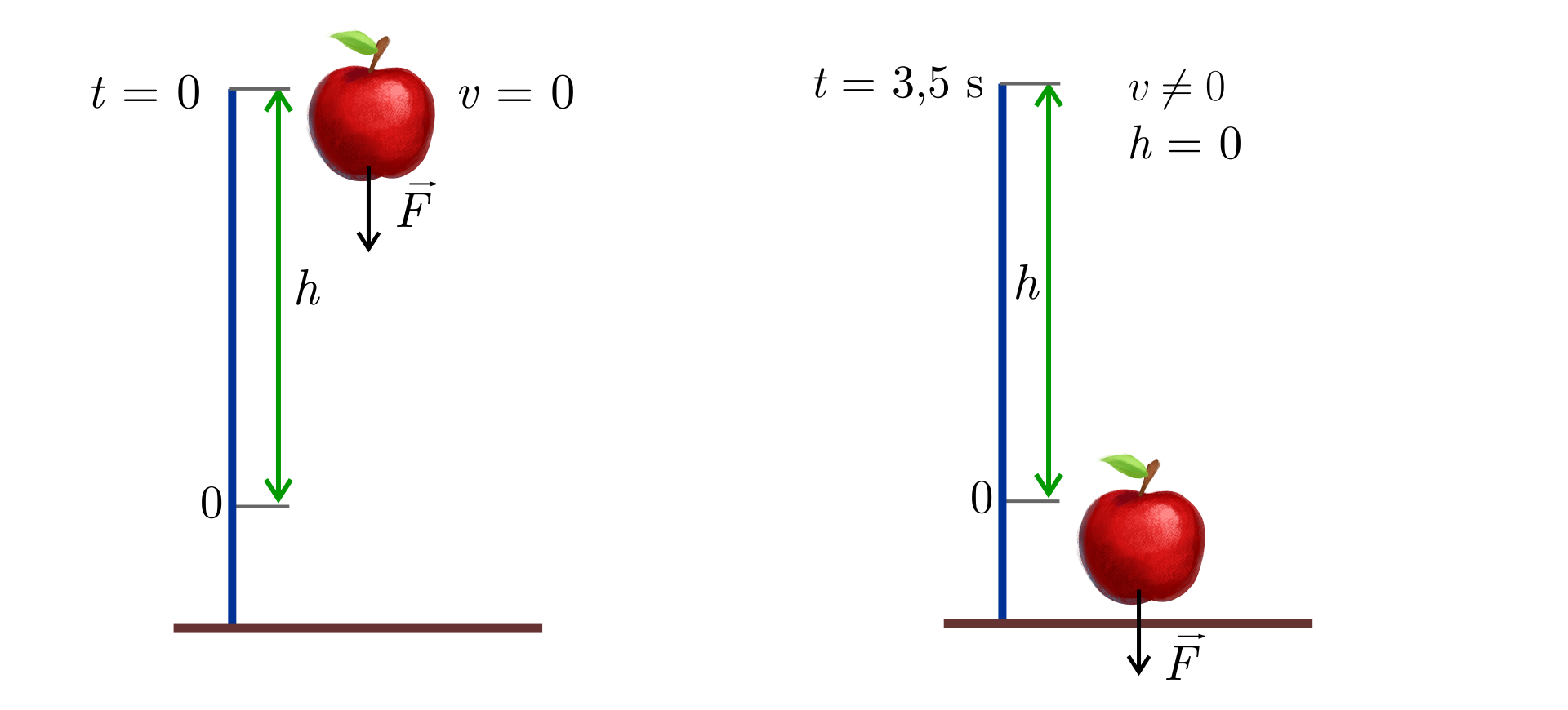
Co to oznacza w przypadku spadku swobodnego?

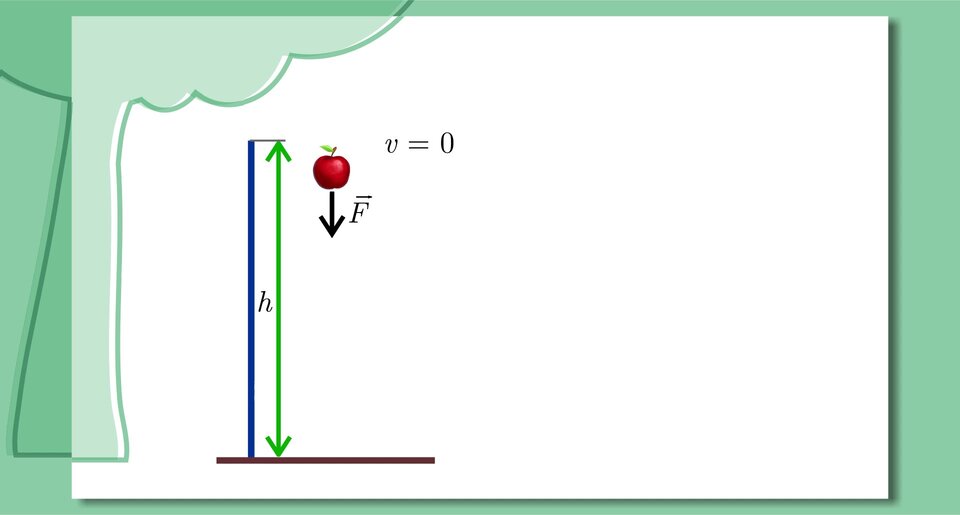
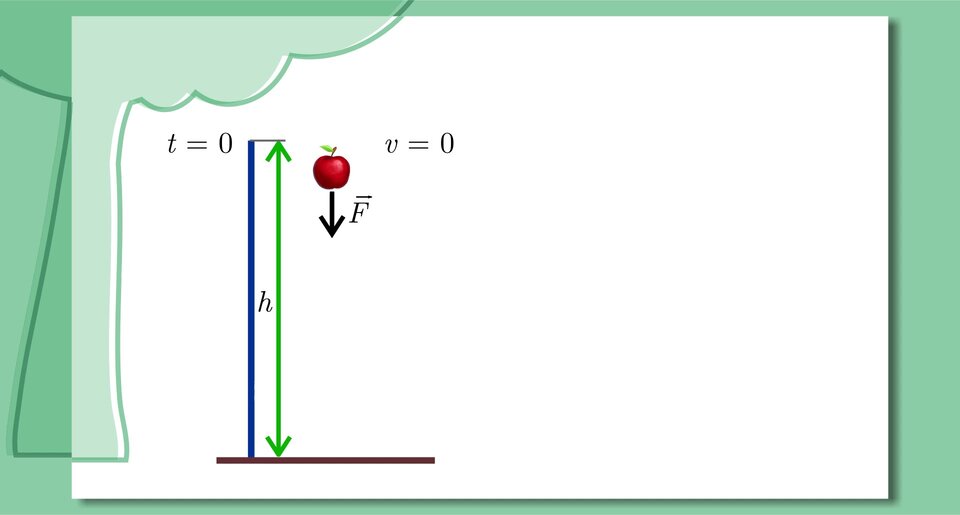
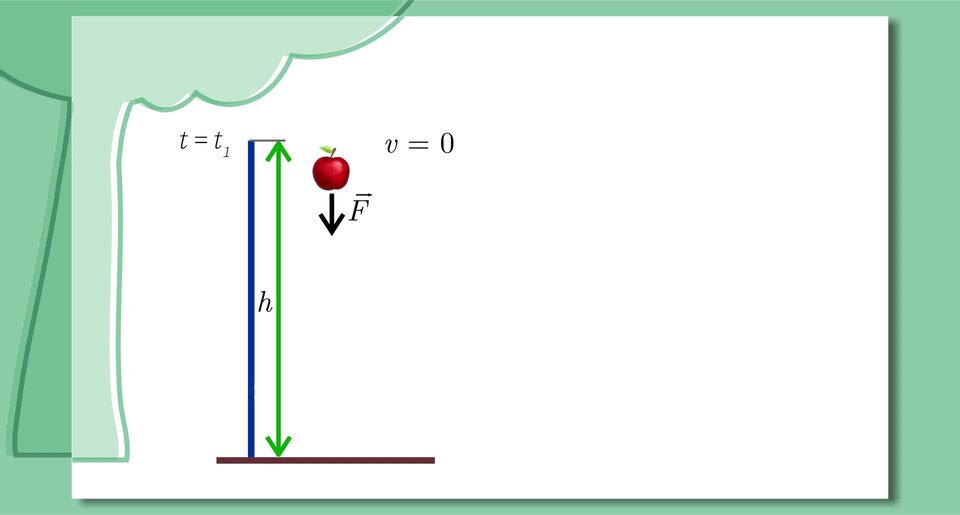
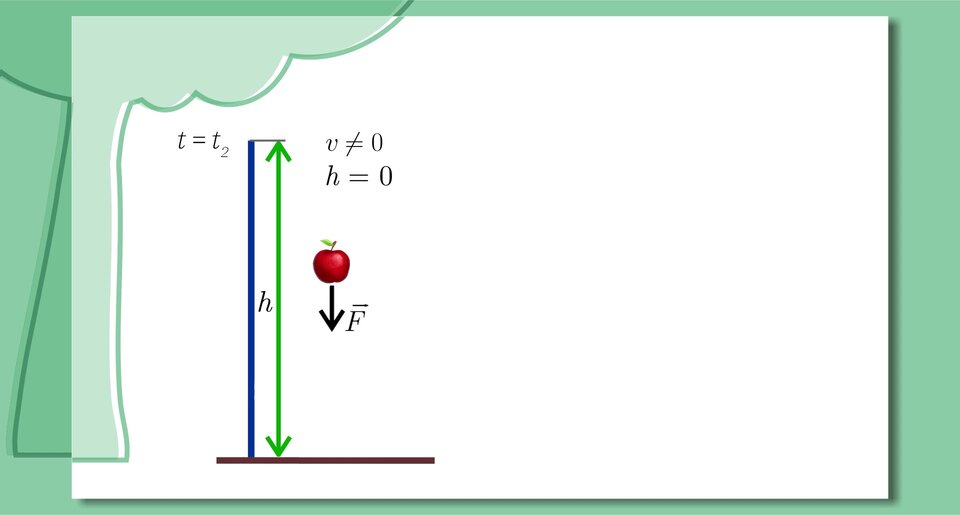
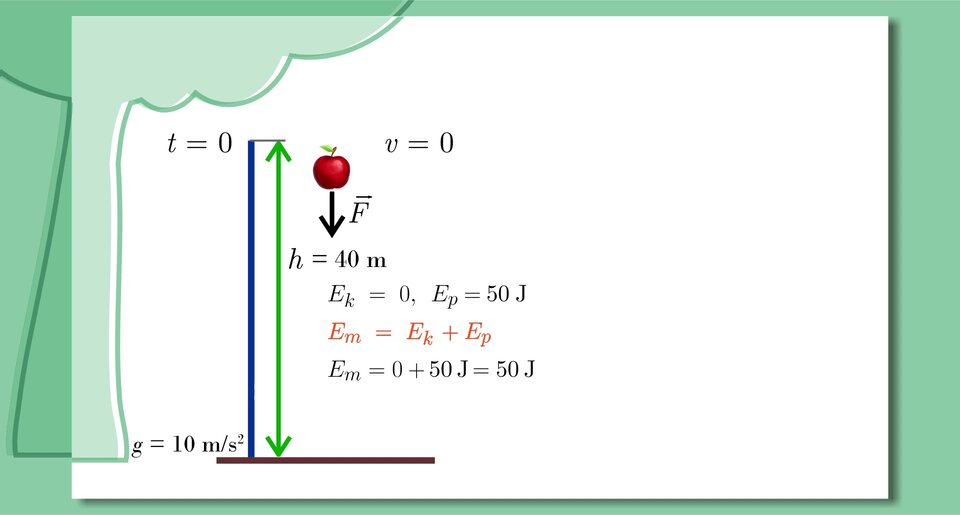
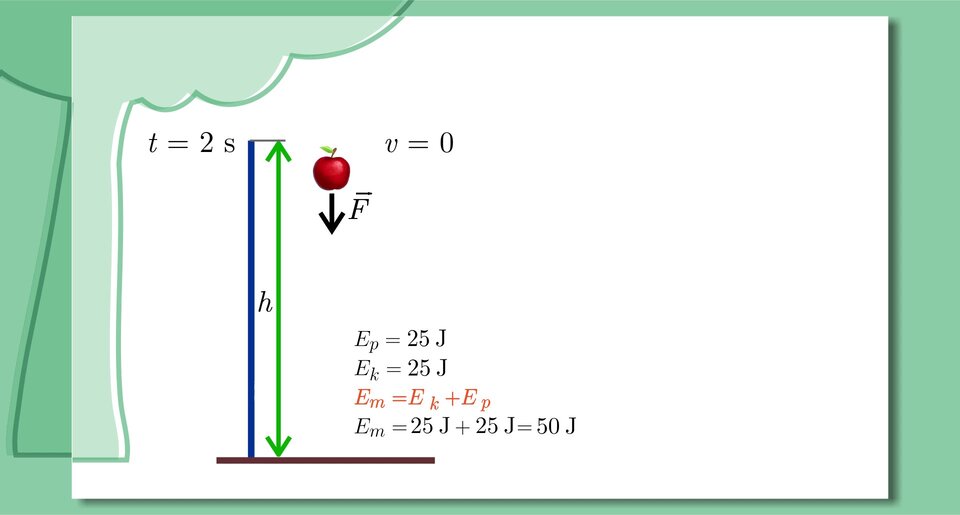
Swobodny spadek jabłka

Zapoznaj się z poniższą prezentacją i na jej podstawie wykonaj znajdujące się pod nią polecenia.

Polecenie 1

RqefXrCHvhnDk1

Widok ozdoby choinkowej w kształcie kuli zawieszonej na drzewku.

Bombka o masie $0,02 \mathrm{kg}$, wisząc na najwyższej gałązce choinki, ma względem podłogi całkowitą energię mechaniczną równą $0,6 \mathrm{J}$. Jaką energię potencjalną posiadałaby, wisząc na gałązce w połowie wysokości choinki? Zakładając, że bombka zaczyna spadać z tej gałązki, określ, ile wyniesie wartość jej energii kinetycznej na chwilę przed uderzeniem o ziemię.

RRAcgPqztnusY

(Uzupełnij).

Pokaż rozwiązanie

Wisząca na najwyższej gałązce choinki bombka posiada tylko energię potencjalną, więc w tym przypadku $E_{\mathrm{m}}=E_{\mathrm{p}}$, w połowie wysokości wartość energii potencjalnej zmaleje o połowę, a więc wyniesie $0,3 \mathrm{J}$. Przed uderzeniem o ziemię całkowita energia mechaniczna będzie równa energii kinetycznej, więc jeśli bombka spada z połowy wysokości choinki, wówczas jej energia kinetyczna wynosi $0,3 \mathrm{J}$. Jeśli spadłaby z najwyższej gałązki, wówczas energia kinetyczna przed uderzeniem o ziemię osiągnęłaby wartość $0,6 \mathrm{J}$.

Sprawdź się

Ćwiczenie 9

Pogrupuj odpowiednio równania opisujące przedstawione na obrazku sytuacje.

R3X8m2bLM1CjL

Dwa obrazki. Na pierwszym sytuacja w chwili początkowej. Jabłko o zerowej prędkości znajduje się na wysokości małe ha, od jabłka poprowadzony w dół wektor duże ef. te równe jest zero i fał równe jest zero. Na dole znajduje się prosta symbolizująca podłoże. Na drugiej ilustracji sytuacja w chwili te równe trzy i pół sekundy. Jabłko o niezerowej prędkości znajduje się na wysokości małe ha równe zero. Od jabłka odchodzi w dół wektor duże ef, identyczny z poprzednim. Jabłko znajduje się przy prostej symbolizującej podłoże.

RZF0pgn8Fxk0O

Jabłko zostaje puszczone: Możliwe odpowiedzi: 1. $E_{\mathrm{k}}=\frac{m{v}^2}{2}$, 2. $E_{\mathrm{m}}=E_{\mathrm{k}}$, 3. $E_{\mathrm{k}}=0$, 4. $E_{\mathrm{p}}=0$, 5. $E_{\mathrm{p}}=mgh$, 6. $E_{\mathrm{m}}=E_{\mathrm{p}}$ Jabłko osiąga wysokość $0$: Możliwe odpowiedzi: 1. $E_{\mathrm{k}}=\frac{m{v}^2}{2}$, 2. $E_{\mathrm{m}}=E_{\mathrm{k}}$, 3. $E_{\mathrm{k}}=0$, 4. $E_{\mathrm{p}}=0$, 5. $E_{\mathrm{p}}=mgh$, 6. $E_{\mathrm{m}}=E_{\mathrm{p}}$

Jabłko zostaje puszczone: Możliwe odpowiedzi: 1. $E_{\mathrm{k}}=\frac{m{v}^2}{2}$, 2. $E_{\mathrm{m}}=E_{\mathrm{k}}$, 3. $E_{\mathrm{k}}=0$, 4. $E_{\mathrm{p}}=0$, 5. $E_{\mathrm{p}}=mgh$, 6. $E_{\mathrm{m}}=E_{\mathrm{p}}$ Jabłko osiąga wysokość $0$: Możliwe odpowiedzi: 1. $E_{\mathrm{k}}=\frac{m{v}^2}{2}$, 2. $E_{\mathrm{m}}=E_{\mathrm{k}}$, 3. $E_{\mathrm{k}}=0$, 4. $E_{\mathrm{p}}=0$, 5. $E_{\mathrm{p}}=mgh$, 6. $E_{\mathrm{m}}=E_{\mathrm{p}}$

Słownik

Bibliografia

Encyklopedia PWN

Sagnowska B., Szot‑Gawlik D., Godlewska M., Rozenbajgier M., Rozenbajgier R., Świat fizyki, Warszawa 2017