Sprawdź się

Pokaż ćwiczenia:

RUcMlq6dxS2fu1

Ćwiczenie 1

Dany jest trójkąt

A B C

. Uporządkuj w odpowiedniej kolejności etapy rysowania okręgu opisanego na tym trójkącie. Elementy do uszeregowania: 1. Konstruujemy symetralne dwóch boków trójkąta

A B C

., 2. Oznaczamy punkt przecięcia symetralnych boków trójkąta jako

O

., 3. Szkicujemy okrąg o środku w punkcie

O

i promieniu długości

A O

., 4. Okrąg o środku w punkcie

O

i promieniu długości

A O

jest okręgiem opisanym na trójkącie

A B C

RbCYu1eoIBwd51

Ćwiczenie 2

R14dTZMvSR4ya1

Ćwiczenie 3

RAms2j1Pg7YOl1

Ćwiczenie 4

R1P2P8ovtbEmv2

Ćwiczenie 5

Wstaw w tekst odpowiednie liczby lub zwroty, które podano poniżej. Jeżeli boki trójkąta mają długości

12

16

oraz 1. symetralne, 2. prostokątny, 3. ostrokątny, 4.

18

, 5.

22

, 6. rozwartokątny, 7. dwusieczne, 8.

20

, 9. środkowe, 10. wysokości, to środek okręgu opisanego na tym trójkącie leży w połowie długości najdłuższego boku tego trójkąta.
Jeżeli środek okręgu opisanego na trójkącie leży na zewnątrz tego trójkąta, to trójkąt jest 1. symetralne, 2. prostokątny, 3. ostrokątny, 4.

18

, 5.

22

, 6. rozwartokątny, 7. dwusieczne, 8.

20

, 9. środkowe, 10. wysokości.
Do wyznaczenia środka okręgu opisanego na dowolnym trójkącie wystarczy skonstruować 1. symetralne, 2. prostokątny, 3. ostrokątny, 4.

18

, 5.

22

, 6. rozwartokątny, 7. dwusieczne, 8.

20

, 9. środkowe, 10. wysokości jego boków.

Ćwiczenie 6

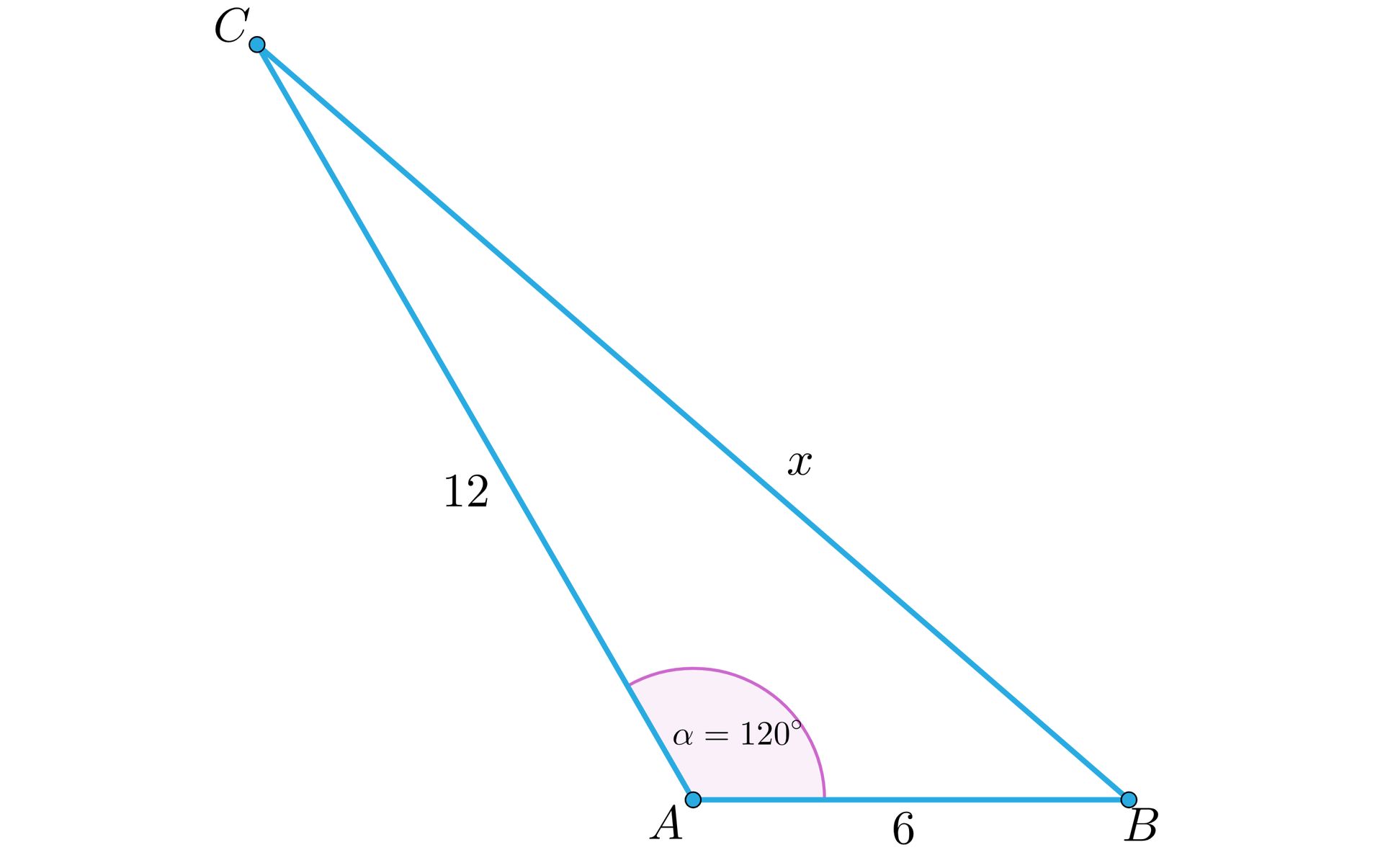
Oblicz długość promienia okręgu opisanego na trójkącie o bokach $12$ i $6$ oraz kącie między nimi o mierze $120 °$ .

R15uaqOpGFmsc

Ilustracja przedstawia trójkąt A B C, w którym kąt CAB jest równy α=120°, bok AB jest równy 6, bok AC jest równy 12, a bok BC jest podpisany literą x.

Przyjmijmy oznaczenia jak na rysunku:

Z twierdzenia cosinusów:

$x^{2} = 12^{2} + 6^{2} - 2 \cdot 12 \cdot 6 \cdot \cos 120 °$

$x^{2} = 144 + 36 + 72$

$x^{2} = 252$

$x = 6 \sqrt{7}$

Z twierdzenia sinusów: $\frac{6 \sqrt{7}}{\sin 120 °} = 2 R$ , zatem: $R = \frac{6 \sqrt{7}}{\frac{\sqrt{3}}{2} \cdot 2} = 2 \sqrt{21}$ .

Długość promienia okręgu opisanego na trójkącie o bokach $12$ i $6$ oraz kącie między nimi o mierze $120 °$ wynosi $R = 2 \sqrt{21}$ .

Ćwiczenie 7

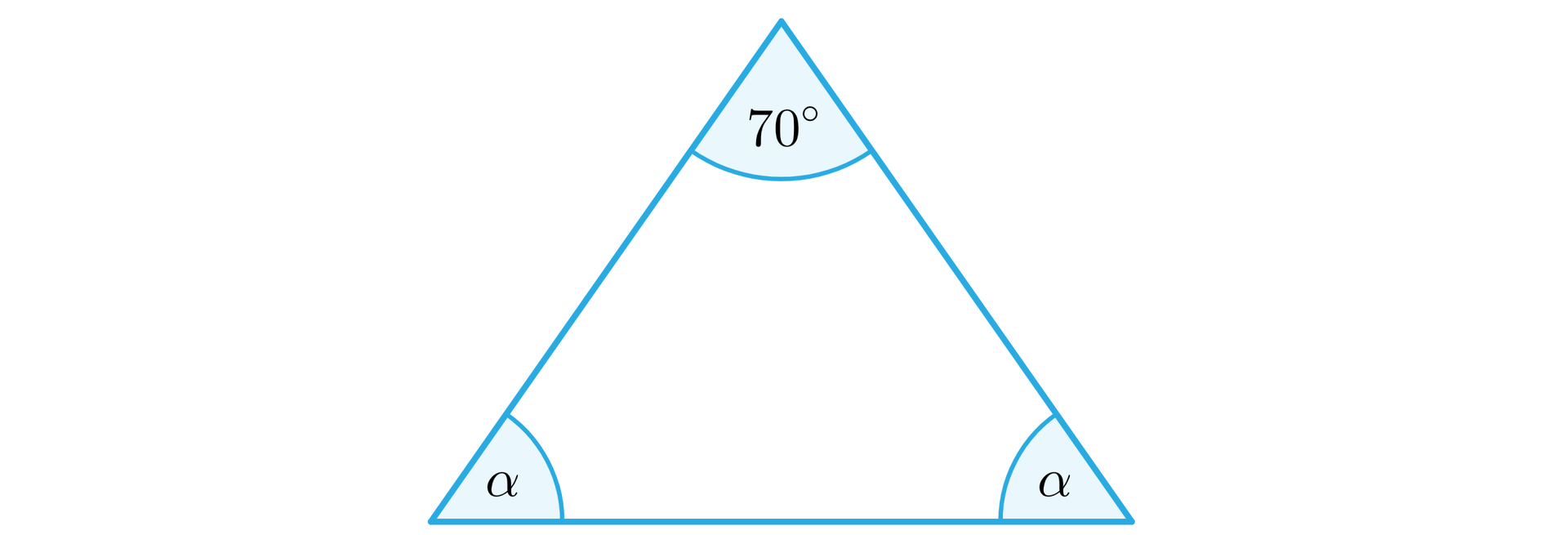
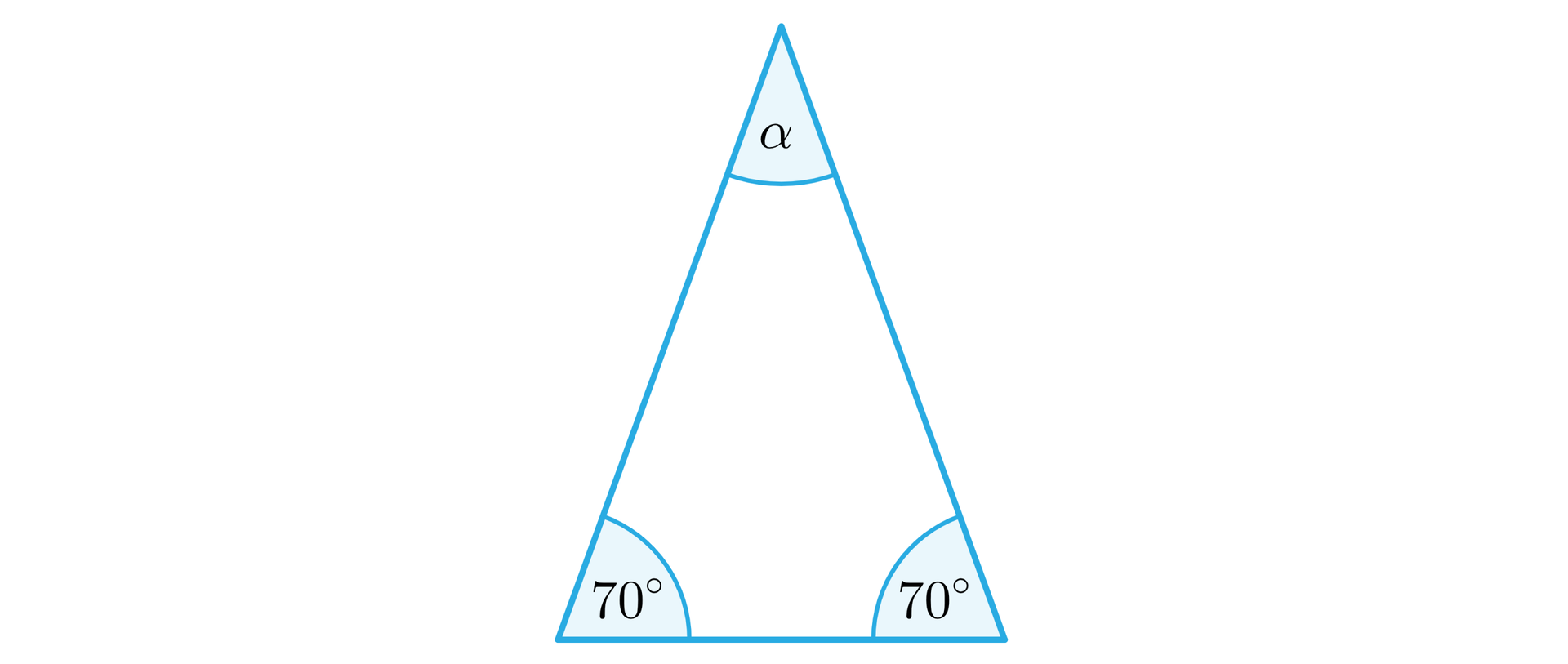
Wiadomo, że jeden z kątów w trójkącie równoramiennym ma miarę $70 °$ . Określ położenie środka okręgu opisanego na tym trójkącie.

Rozpatrzmy dwa przypadki:

gdy podany kąt jest kątem przy wierzchołku trójkąta równoramiennego:
R64QpKmE9xnOJ
Wówczas miara kąta $α$ wynosi:
$α = (180 ° - 70 °) : 2 = 55 °$ .
Zatem trójkąt jest ostrokątny, wobec tego środek okręgu opisanego na tym trójkącie leży wewnątrz trójkąta.

gdy podany kąt jest kątem przy podstawie trójkąta równoramiennego:
RWNzxDCEJKXdq
Wówczas miara kąta $α$ wynosi:
$α = 180 ° - 2 \cdot 70 ° = 40 °$ .
Zatem trójkąt jest ostrokątny, wobec tego środek okręgu opisanego na tym trójkącie leży wewnątrz trójkąta.

Ćwiczenie 8

Oblicz obwód koła opisanego na trójkącie prostokątnym o krótszej przyprostokątnej długości $6 cm$ i kącie ostrym o mierze $60 °$ .

W rozwiązaniu przyda nam się rysunek pomocniczy.

Skoro krótsza przyprostokątna ma długość $6 cm$ , to leży naprzeciw kąta o mierze $30^{0}$ .

RZBWBFEZq1bcF

Ilustracja przedstawia trójkąt prostokątny, którego jedna przyprostokątna ma długość sześć. Kąt przy tej przyprostokątnej ma miarę 60 stopni, a drugi z kątów ostrych ma miarę 30 stopni.

Potrzebujemy długości przeciwprostokątnej, która jest dwa razy dłuższa od krótszej przyprostokątnej, zatem przeciwprostokątna jest długości $12 cm$ .

Obliczyć mamy obwód koła, więc skorzystamy z faktu, że $L = dπ$ , gdzie $d$ jest średnicą tego koła.

Przeciwprostokątna trójkąta jest średnicą koła, zatem $d = 12 cm$ i wówczas $L = 12 π c m$ .

$L = 12 π cm$

Ćwiczenie 9

R1ABGxXHz60rI

RsRsAPAI0uuJq

Aplet

Dla nauczyciela