Sprawdź się
Pokaż ćwiczenia:
Ćwiczenie 1
Ćwiczenie 2
Ćwiczenie 3
Jakie bryły rozpoznajesz na rysunkach? Zaznacz wszystkie poprawne odpowiedzi.
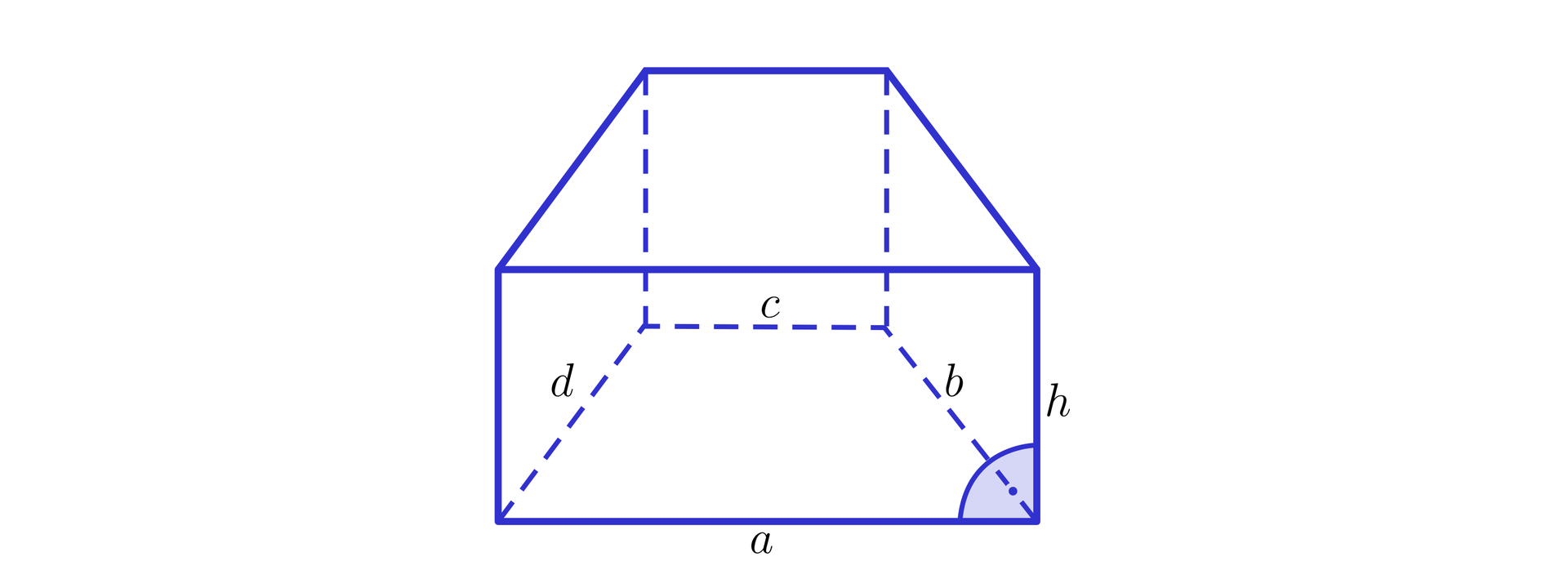
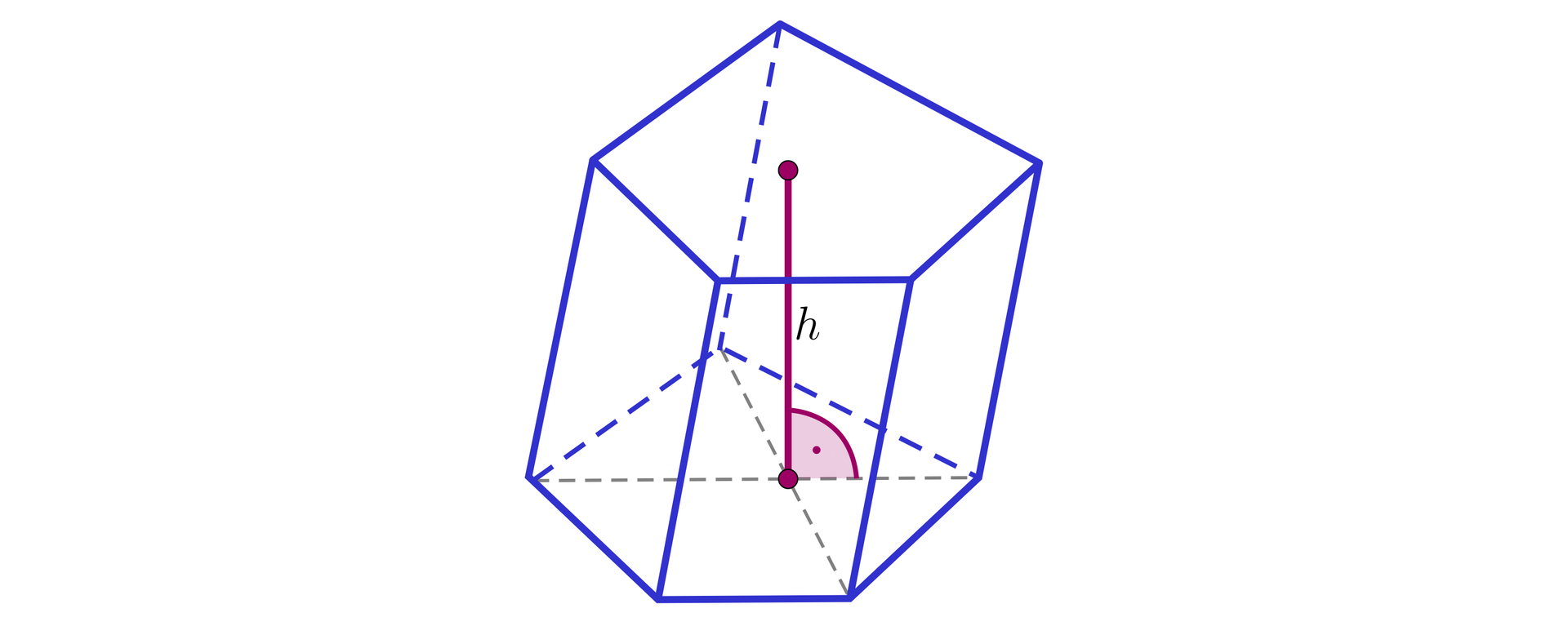
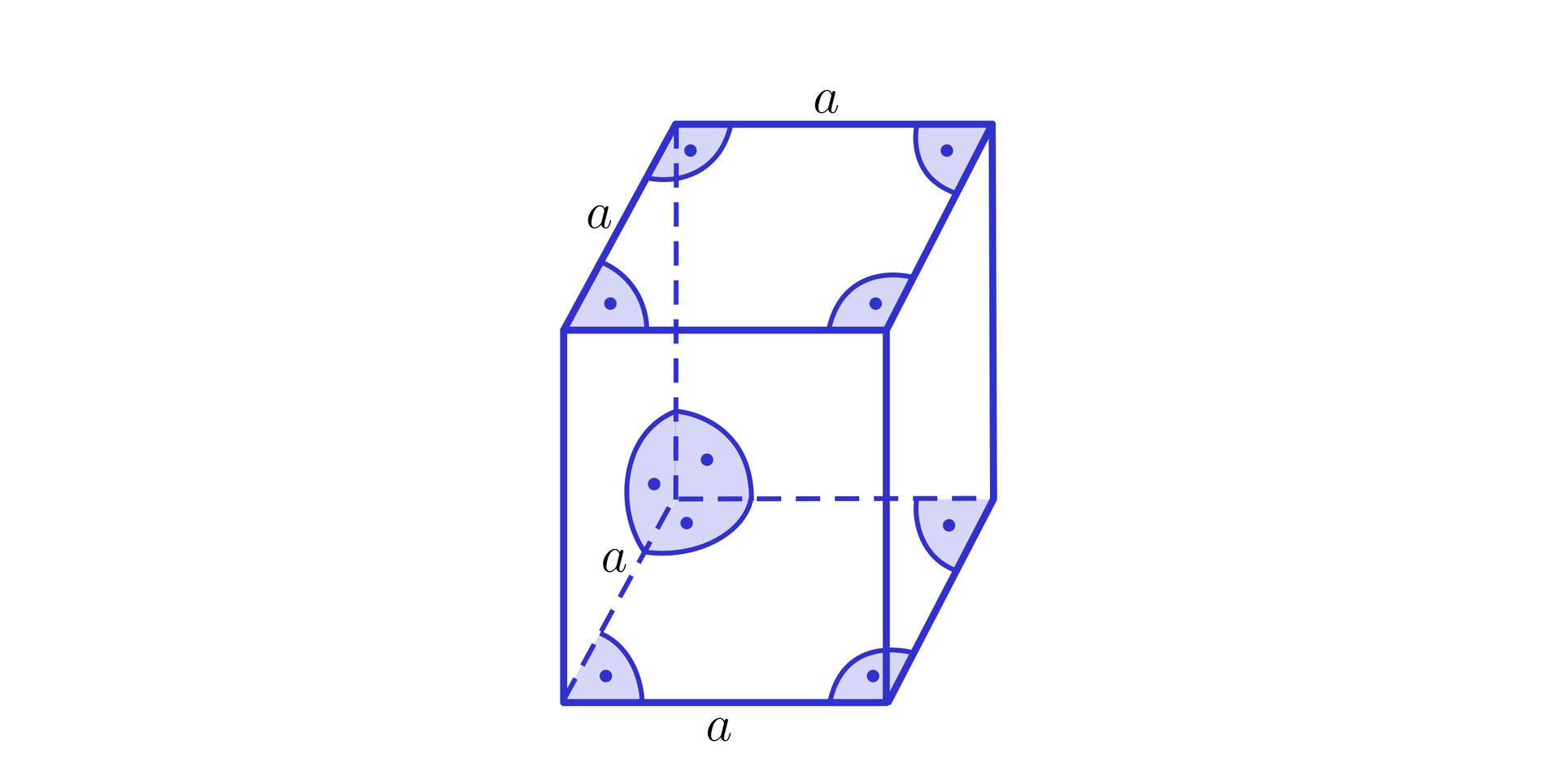
Ćwiczenie 4
Ćwiczenie 5
Ćwiczenie 6
Informacja: Graniastosłup ma , krawędzi.. a. Możliwe odpowiedzi: Nagłówek 2, Nagłówek 3, Nagłówek 3, Nagłówek 3
Ćwiczenie 7
Czy z drutu długości można zbudować szkielet bryły będącej graniastosłupem prawidłowym czworokątnym, w którym długości krawędzi podstaw i długości krawędzi bocznych wyrażone są liczbą całkowitą dodatnią. Rozważ wszystkie możliwości.
Ćwiczenie 8
Jaką maksymalną długość krawędzi bocznej posiada graniastosłup prawidłowy czworokątny, jeśli do budowy jego szkieletu zużyto drut o długości i wiadomo, że długości wszystkich krawędzi są wyrażone przez liczby oraz długość krawędzi podstawy jest najmniejsza z możliwych.