Sprawdź się

Pokaż ćwiczenia:

R1OHULxldyAEx1

Ćwiczenie 1

R1MUPKxQ80CSn2

Ćwiczenie 2

Ile spójnych składowych może mieć graf nieskierowany bez pętli i krwędzi wielokrotnych o 6 wierzchołkach i następującym ciągu stopni wierzchołków.

2, 2, 2, 2, 2, 2 Możliwe odpowiedzi: 1. 1, 2. 2, 3. 3, 4. 6

R16PNIgYtNFjR1

Ćwiczenie 3

RobNyF0oGKt0S11

Ćwiczenie 4

Źródło: Contentplus.pl Sp. z o.o., licencja: CC BY-SA 3.0.

Ćwiczenie 5

Napisz program, który obliczy liczbę spójnych składowych grafu nieskierowanego, a następnie ją wyświetli.

Specyfikacja problemu:

Dane:

n – zmienna statyczna przechowująca liczbę wierzchołków grafu; liczba naturalna
macierzSasiedztwa – macierz sąsiedztwa grafu; tablica dwuwymiarowa liczb naturalnych

Wynik:

liczba spójnych składowych grafu; liczba naturalna

Działanie programu przetestuj dla następujących danych:

Graf:

RHBbzJCeoL0tO

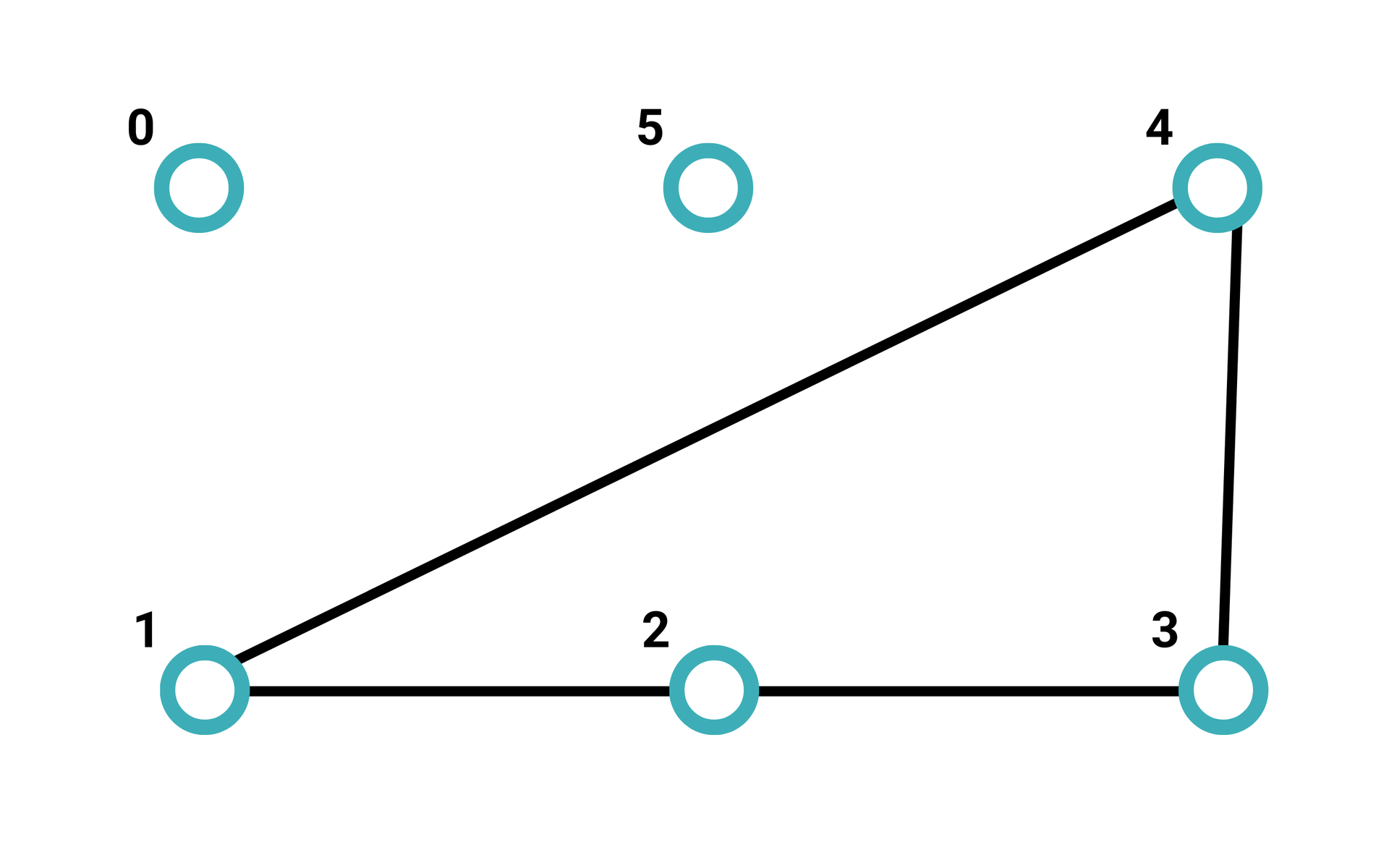
Macierz sąsiedztwa tego grafu:

int[][] macierzSasiedztwa = {
    { 0, 0, 0, 0, 0, 0 },
    { 0, 0, 1, 0, 1, 0 },
    { 0, 1, 0, 1, 0, 0 },
    { 0, 0, 1, 0, 1, 0 },
    { 0, 1, 0, 1, 0, 0 },
	{ 0, 0, 0, 0, 0, 0 }
};

Przykładowy wynik dla podanych danych:

Liczba spojnych skladowych grafu: 3

R1XKe4p8HusfJ

Linia 1. public class Main otwórz nawias klamrowy. Linia 3. private static final int n znak równości 6 średnik. Linia 5. public static void przeszukaj otwórz nawias okrągły int v przecinek boolean otwórz nawias kwadratowy zamknij nawias kwadratowy odwiedzone przecinek int otwórz nawias kwadratowy zamknij nawias kwadratowy otwórz nawias kwadratowy zamknij nawias kwadratowy macierzSasiedztwa zamknij nawias okrągły otwórz nawias klamrowy. Linia 6. odwiedzone otwórz nawias kwadratowy v zamknij nawias kwadratowy znak równości true średnik. Linia 7. for otwórz nawias okrągły int i znak równości 0 średnik i otwórz nawias ostrokątny n średnik i plus plus zamknij nawias okrągły otwórz nawias klamrowy. Linia 8. if otwórz nawias okrągły macierzSasiedztwa otwórz nawias kwadratowy v zamknij nawias kwadratowy otwórz nawias kwadratowy i zamknij nawias kwadratowy znak równości znak równości 1 ampersant ampersant wykrzyknik odwiedzone otwórz nawias kwadratowy i zamknij nawias kwadratowy zamknij nawias okrągły otwórz nawias klamrowy. Linia 9. przeszukaj otwórz nawias okrągły i przecinek odwiedzone przecinek macierzSasiedztwa zamknij nawias okrągły średnik. Linia 10. zamknij nawias klamrowy. Linia 11. zamknij nawias klamrowy. Linia 12. zamknij nawias klamrowy. Linia 14. public static int liczbaSkladowych otwórz nawias okrągły int otwórz nawias kwadratowy zamknij nawias kwadratowy otwórz nawias kwadratowy zamknij nawias kwadratowy macierzSasiedztwa zamknij nawias okrągły otwórz nawias klamrowy. Linia 15. boolean otwórz nawias kwadratowy zamknij nawias kwadratowy odwiedzone znak równości new boolean otwórz nawias kwadratowy n zamknij nawias kwadratowy średnik. Linia 16. int licznikSkladowych znak równości 0 średnik. Linia 18. for otwórz nawias okrągły int i znak równości 0 średnik i otwórz nawias ostrokątny n średnik i plus plus zamknij nawias okrągły otwórz nawias klamrowy. Linia 19. if otwórz nawias okrągły wykrzyknik odwiedzone otwórz nawias kwadratowy i zamknij nawias kwadratowy zamknij nawias okrągły otwórz nawias klamrowy. Linia 20. przeszukaj otwórz nawias okrągły i przecinek odwiedzone przecinek macierzSasiedztwa zamknij nawias okrągły średnik. Linia 21. licznikSkladowych plus plus średnik. Linia 22. zamknij nawias klamrowy. Linia 23. zamknij nawias klamrowy. Linia 25. return licznikSkladowych średnik. Linia 26. zamknij nawias klamrowy. Linia 28. public static void main otwórz nawias okrągły String otwórz nawias kwadratowy zamknij nawias kwadratowy args zamknij nawias okrągły otwórz nawias klamrowy. Linia 29. int otwórz nawias kwadratowy zamknij nawias kwadratowy otwórz nawias kwadratowy zamknij nawias kwadratowy macierzSasiedztwa znak równości otwórz nawias klamrowy. Linia 30. otwórz nawias klamrowy 0 przecinek 0 przecinek 0 przecinek 0 przecinek 0 przecinek 0 zamknij nawias klamrowy przecinek. Linia 31. otwórz nawias klamrowy 0 przecinek 0 przecinek 1 przecinek 0 przecinek 1 przecinek 0 zamknij nawias klamrowy przecinek. Linia 32. otwórz nawias klamrowy 0 przecinek 1 przecinek 0 przecinek 1 przecinek 0 przecinek 0 zamknij nawias klamrowy przecinek. Linia 33. otwórz nawias klamrowy 0 przecinek 0 przecinek 1 przecinek 0 przecinek 1 przecinek 0 zamknij nawias klamrowy przecinek. Linia 34. otwórz nawias klamrowy 0 przecinek 1 przecinek 0 przecinek 1 przecinek 0 przecinek 0 zamknij nawias klamrowy przecinek. Linia 35. otwórz nawias klamrowy 0 przecinek 0 przecinek 0 przecinek 0 przecinek 0 przecinek 0 zamknij nawias klamrowy. Linia 36. zamknij nawias klamrowy średnik. Linia 38. System kropka out kropka println otwórz nawias okrągły cudzysłów Liczba spojnych skladowych grafu dwukropek cudzysłów plus liczbaSkladowych otwórz nawias okrągły macierzSasiedztwa zamknij nawias okrągły zamknij nawias okrągły średnik. Linia 39. zamknij nawias klamrowy. Linia 40. zamknij nawias klamrowy.

public class Main {

    private static final int n = 6;

    public static void przeszukaj(int v, boolean[] odwiedzone, int[][] macierzSasiedztwa) {
        odwiedzone[v] = true;
        for (int i = 0; i < n; i++) {
            if (macierzSasiedztwa[v][i] == 1 && !odwiedzone[i]) {
                przeszukaj(i, odwiedzone, macierzSasiedztwa);
            }
        }
    }

    public static int liczbaSkladowych(int[][] macierzSasiedztwa) {
        boolean[] odwiedzone = new boolean[n];
        int licznikSkladowych = 0;

        for (int i = 0; i < n; i++) {
            if (!odwiedzone[i]) {
                przeszukaj(i, odwiedzone, macierzSasiedztwa);
                licznikSkladowych++;
            }
        }

        return licznikSkladowych;
    }

    public static void main(String[] args) {
        int[][] macierzSasiedztwa = {
            { 0, 0, 0, 0, 0, 0 },
            { 0, 0, 1, 0, 1, 0 },
            { 0, 1, 0, 1, 0, 0 },
            { 0, 0, 1, 0, 1, 0 },
            { 0, 1, 0, 1, 0, 0 },
            { 0, 0, 0, 0, 0, 0 }
        };

        System.out.println("Liczba spojnych skladowych grafu: " + liczbaSkladowych(macierzSasiedztwa));
    }
}

Ćwiczenie 6

Napisz program, który sprawdzi, czy dana para wierzchołków o indeksach v oraz w tworzących krawędź vw grafu spójnego nieskierowanego reprezentowanego przez macierz sąsiedztwa jest mostem.

Specyfikacja problemu:

Dane:

n – zmienna statyczna przechowująca liczbę wierzchołków grafu; liczba naturalna
macierzSasiedztwa – macierz sąsiedztwa grafu; tablica dwuwymiarowa liczb naturalnych
v – indeks wierzchołka tworzącego krawędź; liczba naturalna
w – indeks wierzchołka tworzącego krawędź; liczba naturalna

Wynik:

komunikat informujący o tym, czy krawędź tworzona przez dwa podane wierzchołki vw jest mostem

Działanie programu przetestuj dla następujących danych:

Graf:

RiOppoLhKXNb6

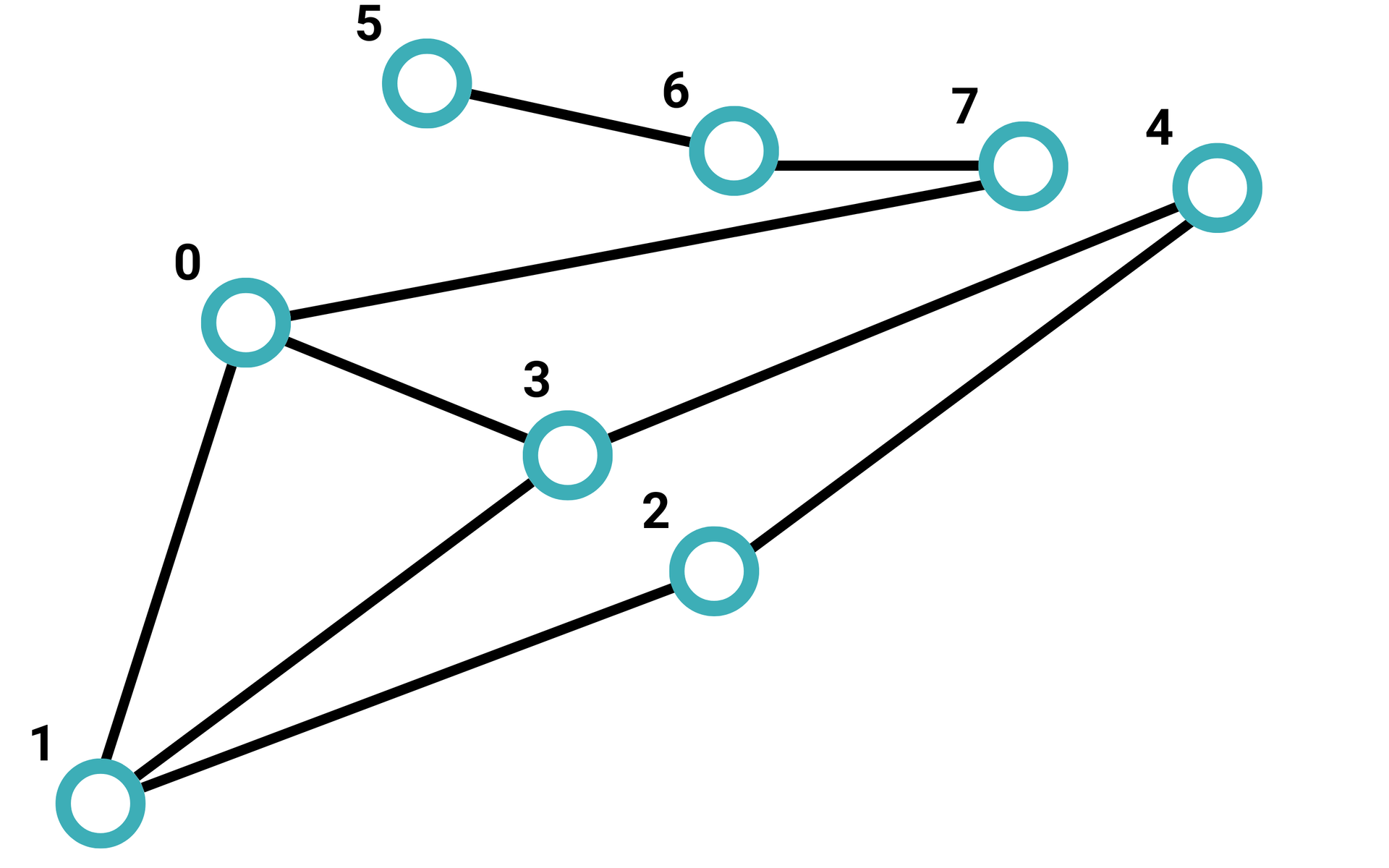
Macierz sąsiedztwa grafu:

int[][] macierzSasiedztwa = {
    { 0, 1, 0, 1, 0, 0, 0, 1 },
    { 1, 0, 1, 1, 0, 0, 0, 0 },
    { 0, 1, 0, 0, 1, 0, 0, 0 },
    { 1, 1, 0, 0, 1, 0, 0, 0 },
    { 0, 0, 1, 1, 0, 0, 0, 0 },
    { 0, 0, 0, 0, 0, 0, 1, 0 },
    { 0, 0, 0, 0, 0, 1, 0, 1 },
    { 1, 0, 0, 0, 0, 0, 1, 0 }
};

int v = 0;
int w = 7;

Przykładowy wynik dla podanych danych:

Krawedz 0-7 jest mostem

R2WnbUM2irWC9

Linia 1. public class Main otwórz nawias klamrowy. Linia 2. private static final int n znak równości 8 średnik. Linia 4. public static void przeszukaj otwórz nawias okrągły int v przecinek boolean otwórz nawias kwadratowy zamknij nawias kwadratowy odwiedzone przecinek int otwórz nawias kwadratowy zamknij nawias kwadratowy otwórz nawias kwadratowy zamknij nawias kwadratowy macierzSasiedztwa zamknij nawias okrągły otwórz nawias klamrowy. Linia 5. odwiedzone otwórz nawias kwadratowy v zamknij nawias kwadratowy znak równości true średnik. Linia 6. for otwórz nawias okrągły int i znak równości 0 średnik i otwórz nawias ostrokątny n średnik i plus plus zamknij nawias okrągły otwórz nawias klamrowy. Linia 7. if otwórz nawias okrągły macierzSasiedztwa otwórz nawias kwadratowy v zamknij nawias kwadratowy otwórz nawias kwadratowy i zamknij nawias kwadratowy znak równości znak równości 1 ampersant ampersant wykrzyknik odwiedzone otwórz nawias kwadratowy i zamknij nawias kwadratowy zamknij nawias okrągły otwórz nawias klamrowy. Linia 8. przeszukaj otwórz nawias okrągły i przecinek odwiedzone przecinek macierzSasiedztwa zamknij nawias okrągły średnik. Linia 9. zamknij nawias klamrowy. Linia 10. zamknij nawias klamrowy. Linia 11. zamknij nawias klamrowy. Linia 13. public static int liczbaSkladowych otwórz nawias okrągły int otwórz nawias kwadratowy zamknij nawias kwadratowy otwórz nawias kwadratowy zamknij nawias kwadratowy macierzSasiedztwa zamknij nawias okrągły otwórz nawias klamrowy. Linia 14. boolean otwórz nawias kwadratowy zamknij nawias kwadratowy odwiedzone znak równości new boolean otwórz nawias kwadratowy n zamknij nawias kwadratowy średnik. Linia 15. int licznikSkladowych znak równości 0 średnik. Linia 17. for otwórz nawias okrągły int i znak równości 0 średnik i otwórz nawias ostrokątny n średnik i plus plus zamknij nawias okrągły otwórz nawias klamrowy. Linia 18. if otwórz nawias okrągły wykrzyknik odwiedzone otwórz nawias kwadratowy i zamknij nawias kwadratowy zamknij nawias okrągły otwórz nawias klamrowy. Linia 19. przeszukaj otwórz nawias okrągły i przecinek odwiedzone przecinek macierzSasiedztwa zamknij nawias okrągły średnik. Linia 20. licznikSkladowych plus plus średnik. Linia 21. zamknij nawias klamrowy. Linia 22. zamknij nawias klamrowy. Linia 24. return licznikSkladowych średnik. Linia 25. zamknij nawias klamrowy. Linia 27. public static boolean czyMost otwórz nawias okrągły int v przecinek int w przecinek int otwórz nawias kwadratowy zamknij nawias kwadratowy otwórz nawias kwadratowy zamknij nawias kwadratowy macierzSasiedztwa zamknij nawias okrągły otwórz nawias klamrowy. Linia 28. macierzSasiedztwa otwórz nawias kwadratowy v zamknij nawias kwadratowy otwórz nawias kwadratowy w zamknij nawias kwadratowy znak równości 0 średnik. Linia 29. macierzSasiedztwa otwórz nawias kwadratowy w zamknij nawias kwadratowy otwórz nawias kwadratowy v zamknij nawias kwadratowy znak równości 0 średnik. Linia 30. int nowaLiczba znak równości liczbaSkladowych otwórz nawias okrągły macierzSasiedztwa zamknij nawias okrągły średnik. Linia 31. macierzSasiedztwa otwórz nawias kwadratowy v zamknij nawias kwadratowy otwórz nawias kwadratowy w zamknij nawias kwadratowy znak równości 1 średnik. Linia 32. macierzSasiedztwa otwórz nawias kwadratowy w zamknij nawias kwadratowy otwórz nawias kwadratowy v zamknij nawias kwadratowy znak równości 1 średnik. Linia 34. return liczbaSkladowych otwórz nawias okrągły macierzSasiedztwa zamknij nawias okrągły wykrzyknik znak równości nowaLiczba średnik. Linia 35. zamknij nawias klamrowy. Linia 37. public static void main otwórz nawias okrągły String otwórz nawias kwadratowy zamknij nawias kwadratowy args zamknij nawias okrągły otwórz nawias klamrowy. Linia 38. int otwórz nawias kwadratowy zamknij nawias kwadratowy otwórz nawias kwadratowy zamknij nawias kwadratowy macierzSasiedztwa znak równości otwórz nawias klamrowy. Linia 39. otwórz nawias klamrowy 0 przecinek 1 przecinek 0 przecinek 1 przecinek 0 przecinek 0 przecinek 0 przecinek 1 zamknij nawias klamrowy przecinek. Linia 40. otwórz nawias klamrowy 1 przecinek 0 przecinek 1 przecinek 1 przecinek 0 przecinek 0 przecinek 0 przecinek 0 zamknij nawias klamrowy przecinek. Linia 41. otwórz nawias klamrowy 0 przecinek 1 przecinek 0 przecinek 0 przecinek 1 przecinek 0 przecinek 0 przecinek 0 zamknij nawias klamrowy przecinek. Linia 42. otwórz nawias klamrowy 1 przecinek 1 przecinek 0 przecinek 0 przecinek 1 przecinek 0 przecinek 0 przecinek 0 zamknij nawias klamrowy przecinek. Linia 43. otwórz nawias klamrowy 0 przecinek 0 przecinek 1 przecinek 1 przecinek 0 przecinek 0 przecinek 0 przecinek 0 zamknij nawias klamrowy przecinek. Linia 44. otwórz nawias klamrowy 0 przecinek 0 przecinek 0 przecinek 0 przecinek 0 przecinek 0 przecinek 1 przecinek 0 zamknij nawias klamrowy przecinek. Linia 45. otwórz nawias klamrowy 0 przecinek 0 przecinek 0 przecinek 0 przecinek 0 przecinek 1 przecinek 0 przecinek 1 zamknij nawias klamrowy przecinek. Linia 46. otwórz nawias klamrowy 1 przecinek 0 przecinek 0 przecinek 0 przecinek 0 przecinek 0 przecinek 1 przecinek 0 zamknij nawias klamrowy. Linia 47. zamknij nawias klamrowy średnik. Linia 49. int v znak równości 0 średnik. Linia 50. int w znak równości 7 średnik. Linia 51. System kropka out kropka print otwórz nawias okrągły cudzysłów Krawedz cudzysłów plus v plus cudzysłów minus cudzysłów plus w plus cudzysłów cudzysłów zamknij nawias okrągły średnik. Linia 52. if otwórz nawias okrągły czyMost otwórz nawias okrągły v przecinek w przecinek macierzSasiedztwa zamknij nawias okrągły zamknij nawias okrągły. Linia 53. System kropka out kropka println otwórz nawias okrągły cudzysłów jest mostem cudzysłów zamknij nawias okrągły średnik. Linia 54. else. Linia 55. System kropka out kropka println otwórz nawias okrągły cudzysłów nie jest mostem cudzysłów zamknij nawias okrągły średnik. Linia 56. zamknij nawias klamrowy. Linia 57. zamknij nawias klamrowy.

public class Main {
    private static final int n = 8;

    public static void przeszukaj(int v, boolean[] odwiedzone, int[][] macierzSasiedztwa) {
        odwiedzone[v] = true;
        for (int i = 0; i < n; i++) {
            if (macierzSasiedztwa[v][i] == 1 && !odwiedzone[i]) {
                przeszukaj(i, odwiedzone, macierzSasiedztwa);
            }
        }
    }

    public static int liczbaSkladowych(int[][] macierzSasiedztwa) {
        boolean[] odwiedzone = new boolean[n];
        int licznikSkladowych = 0;

        for (int i = 0; i < n; i++) {
            if (!odwiedzone[i]) {
                przeszukaj(i, odwiedzone, macierzSasiedztwa);
                licznikSkladowych++;
            }
        }

        return licznikSkladowych;
    }

    public static boolean czyMost(int v, int w, int[][] macierzSasiedztwa) {
        macierzSasiedztwa[v][w] = 0;
        macierzSasiedztwa[w][v] = 0;
        int nowaLiczba = liczbaSkladowych(macierzSasiedztwa);
        macierzSasiedztwa[v][w] = 1;
        macierzSasiedztwa[w][v] = 1;

        return liczbaSkladowych(macierzSasiedztwa) != nowaLiczba;
    }

    public static void main(String[] args) {
        int[][] macierzSasiedztwa = {
            { 0, 1, 0, 1, 0, 0, 0, 1 },
            { 1, 0, 1, 1, 0, 0, 0, 0 },
            { 0, 1, 0, 0, 1, 0, 0, 0 },
            { 1, 1, 0, 0, 1, 0, 0, 0 },
            { 0, 0, 1, 1, 0, 0, 0, 0 },
            { 0, 0, 0, 0, 0, 0, 1, 0 },
            { 0, 0, 0, 0, 0, 1, 0, 1 },
            { 1, 0, 0, 0, 0, 0, 1, 0 }
        };

        int v = 0;
        int w = 7;
        System.out.print("Krawedz " + v + "-" + w + " ");
        if (czyMost(v, w, macierzSasiedztwa))
            System.out.println("jest mostem");
        else
            System.out.println("nie jest mostem");
    }
}

Dla zainteresowanych

Ćwiczenie 7

Napisz program, który sprawdzi, czy dla danego digrafu reprezentowanego przez macierz sąsiedztwa możliwe jest dojście z wierzchołka startowego (o indeksie startowy) do wierzchołka końcowego (o indeksie koncowy).

Specyfikacja problemu:

Dane:

n – zmienna statyczna przechowująca liczbę wierzchołków grafu; liczba naturalna
macierzSasiedztwa – macierz sąsiedztwa grafu; tablica dwuwymiarowa liczb naturalnych
startowy – indeks wierzchołka; liczba naturalna
koncowy – indeks wierzchołka; liczba naturalna

Wynik:

komunikat informujący o tym, czy możliwe jest dojście z wierzchołka startowy do wierzchołka koncowy

Działanie programu przetestuj dla następujących danych:

Graf:

R1ACJIqAG7ZTa

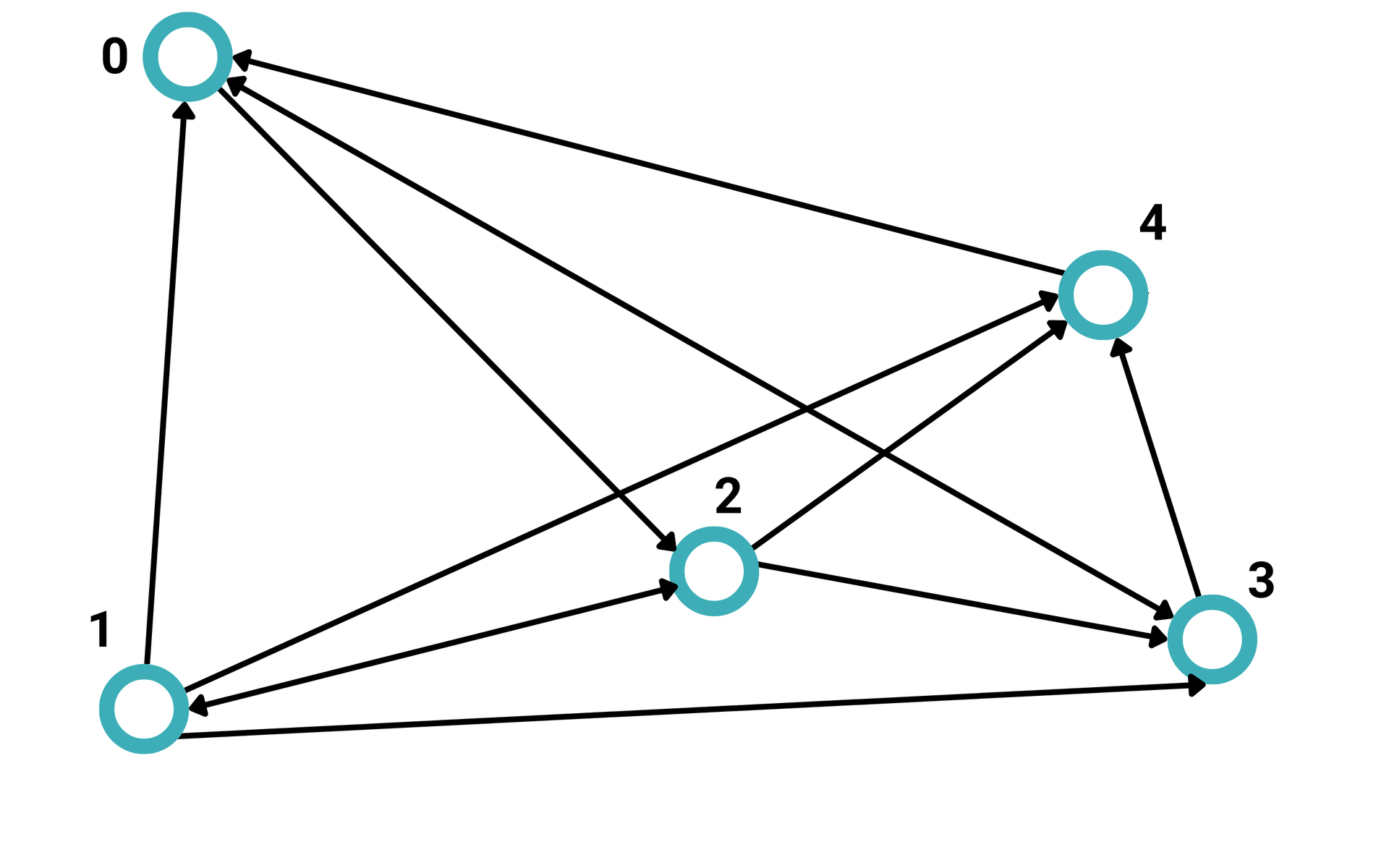
Macierz sąsiedztwa grafu:

int[][] macierzSasiedztwa = {
	{ 0, 0, 1, 1, 0 },
    { 1, 0, 1, 1, 1 },
    { 0, 1, 0, 1, 1 },
    { 1, 0, 0, 0, 1 },
    { 1, 0, 0, 0, 0 }
};

int startowy = 0;
int koncowy = 4;

Przykładowy wynik dla podanych danych:

Wierzcholek 4 jest osiagalny z wierzcholka 0

R12Dflqum2lxn

Linia 1. public class Main otwórz nawias klamrowy. Linia 2. static final int n znak równości 5 średnik. Linia 4. static boolean przeszukaj otwórz nawias okrągły int v przecinek boolean otwórz nawias kwadratowy zamknij nawias kwadratowy odwiedzone przecinek int otwórz nawias kwadratowy zamknij nawias kwadratowy otwórz nawias kwadratowy zamknij nawias kwadratowy macierzSasiedztwa przecinek int docelowy zamknij nawias okrągły otwórz nawias klamrowy. Linia 5. odwiedzone otwórz nawias kwadratowy v zamknij nawias kwadratowy znak równości true średnik. Linia 6. if otwórz nawias okrągły v znak równości znak równości docelowy zamknij nawias okrągły otwórz nawias klamrowy. Linia 7. return true średnik. Linia 8. zamknij nawias klamrowy. Linia 10. for otwórz nawias okrągły int w znak równości 0 średnik w otwórz nawias ostrokątny n średnik w plus plus zamknij nawias okrągły otwórz nawias klamrowy. Linia 11. if otwórz nawias okrągły macierzSasiedztwa otwórz nawias kwadratowy v zamknij nawias kwadratowy otwórz nawias kwadratowy w zamknij nawias kwadratowy znak równości znak równości 1 ampersant ampersant wykrzyknik odwiedzone otwórz nawias kwadratowy w zamknij nawias kwadratowy zamknij nawias okrągły otwórz nawias klamrowy. Linia 12. if otwórz nawias okrągły przeszukaj otwórz nawias okrągły w przecinek odwiedzone przecinek macierzSasiedztwa przecinek docelowy zamknij nawias okrągły zamknij nawias okrągły otwórz nawias klamrowy. Linia 13. return true średnik. Linia 14. zamknij nawias klamrowy. Linia 15. zamknij nawias klamrowy. Linia 16. zamknij nawias klamrowy. Linia 18. return false średnik. Linia 19. zamknij nawias klamrowy. Linia 21. static boolean czyOsiagalny otwórz nawias okrągły int otwórz nawias kwadratowy zamknij nawias kwadratowy otwórz nawias kwadratowy zamknij nawias kwadratowy macierzSasiedztwa przecinek int startowy przecinek int koncowy zamknij nawias okrągły otwórz nawias klamrowy. Linia 22. boolean otwórz nawias kwadratowy zamknij nawias kwadratowy odwiedzone znak równości new boolean otwórz nawias kwadratowy n zamknij nawias kwadratowy średnik. Linia 23. return przeszukaj otwórz nawias okrągły startowy przecinek odwiedzone przecinek macierzSasiedztwa przecinek koncowy zamknij nawias okrągły średnik. Linia 24. zamknij nawias klamrowy. Linia 26. public static void main otwórz nawias okrągły String otwórz nawias kwadratowy zamknij nawias kwadratowy args zamknij nawias okrągły otwórz nawias klamrowy. Linia 27. int otwórz nawias kwadratowy zamknij nawias kwadratowy otwórz nawias kwadratowy zamknij nawias kwadratowy macierzSasiedztwa znak równości otwórz nawias klamrowy. Linia 28. otwórz nawias klamrowy 0 przecinek 0 przecinek 1 przecinek 1 przecinek 0 zamknij nawias klamrowy przecinek. Linia 29. otwórz nawias klamrowy 1 przecinek 0 przecinek 1 przecinek 1 przecinek 1 zamknij nawias klamrowy przecinek. Linia 30. otwórz nawias klamrowy 0 przecinek 1 przecinek 0 przecinek 1 przecinek 1 zamknij nawias klamrowy przecinek. Linia 31. otwórz nawias klamrowy 1 przecinek 0 przecinek 0 przecinek 0 przecinek 1 zamknij nawias klamrowy przecinek. Linia 32. otwórz nawias klamrowy 1 przecinek 0 przecinek 0 przecinek 0 przecinek 0 zamknij nawias klamrowy. Linia 33. zamknij nawias klamrowy średnik. Linia 35. int startowy znak równości 0 średnik. Linia 36. int koncowy znak równości 4 średnik. Linia 38. if otwórz nawias okrągły czyOsiagalny otwórz nawias okrągły macierzSasiedztwa przecinek startowy przecinek koncowy zamknij nawias okrągły zamknij nawias okrągły otwórz nawias klamrowy. Linia 39. System kropka out kropka println otwórz nawias okrągły cudzysłów Wierzcholek cudzysłów plus koncowy plus cudzysłów jest osiagalny z wierzcholka cudzysłów plus startowy zamknij nawias okrągły średnik. Linia 40. zamknij nawias klamrowy else otwórz nawias klamrowy. Linia 41. System kropka out kropka println otwórz nawias okrągły cudzysłów Wierzcholek cudzysłów plus koncowy plus cudzysłów nie jest osiagalny z wierzcholka cudzysłów plus startowy zamknij nawias okrągły średnik. Linia 42. zamknij nawias klamrowy. Linia 43. zamknij nawias klamrowy. Linia 44. zamknij nawias klamrowy.

public class Main {
    static final int n = 5;

    static boolean przeszukaj(int v, boolean[] odwiedzone, int[][] macierzSasiedztwa, int docelowy) {
        odwiedzone[v] = true;
        if (v == docelowy) {
            return true;
        }

        for (int w = 0; w < n; w++) {
            if (macierzSasiedztwa[v][w] == 1 && !odwiedzone[w]) {
                if (przeszukaj(w, odwiedzone, macierzSasiedztwa, docelowy)) {
                    return true;
                }
            }
        }

        return false;
    }

    static boolean czyOsiagalny(int[][] macierzSasiedztwa, int startowy, int koncowy) {
        boolean[] odwiedzone = new boolean[n];
        return przeszukaj(startowy, odwiedzone, macierzSasiedztwa, koncowy);
    }

    public static void main(String[] args) {
        int[][] macierzSasiedztwa = {
            { 0, 0, 1, 1, 0 },
            { 1, 0, 1, 1, 1 },
            { 0, 1, 0, 1, 1 },
            { 1, 0, 0, 0, 1 },
            { 1, 0, 0, 0, 0 }
        };

        int startowy = 0;
        int koncowy = 4;

        if (czyOsiagalny(macierzSasiedztwa, startowy, koncowy)) {
            System.out.println("Wierzcholek " + koncowy + " jest osiagalny z wierzcholka " + startowy);
        } else {
            System.out.println("Wierzcholek " + koncowy + " nie jest osiagalny z wierzcholka " + startowy);
        }
    }
}

Prezentacja multimedialna

Dla nauczyciela