Sprawdź się
Spośród wielościanów wybierz wielościany wypukłe.
- Opis poprawnej ilustracji A
- Opis ilustracji B
- Opis ilustracji C
- Opis poprawnej ilustracji D

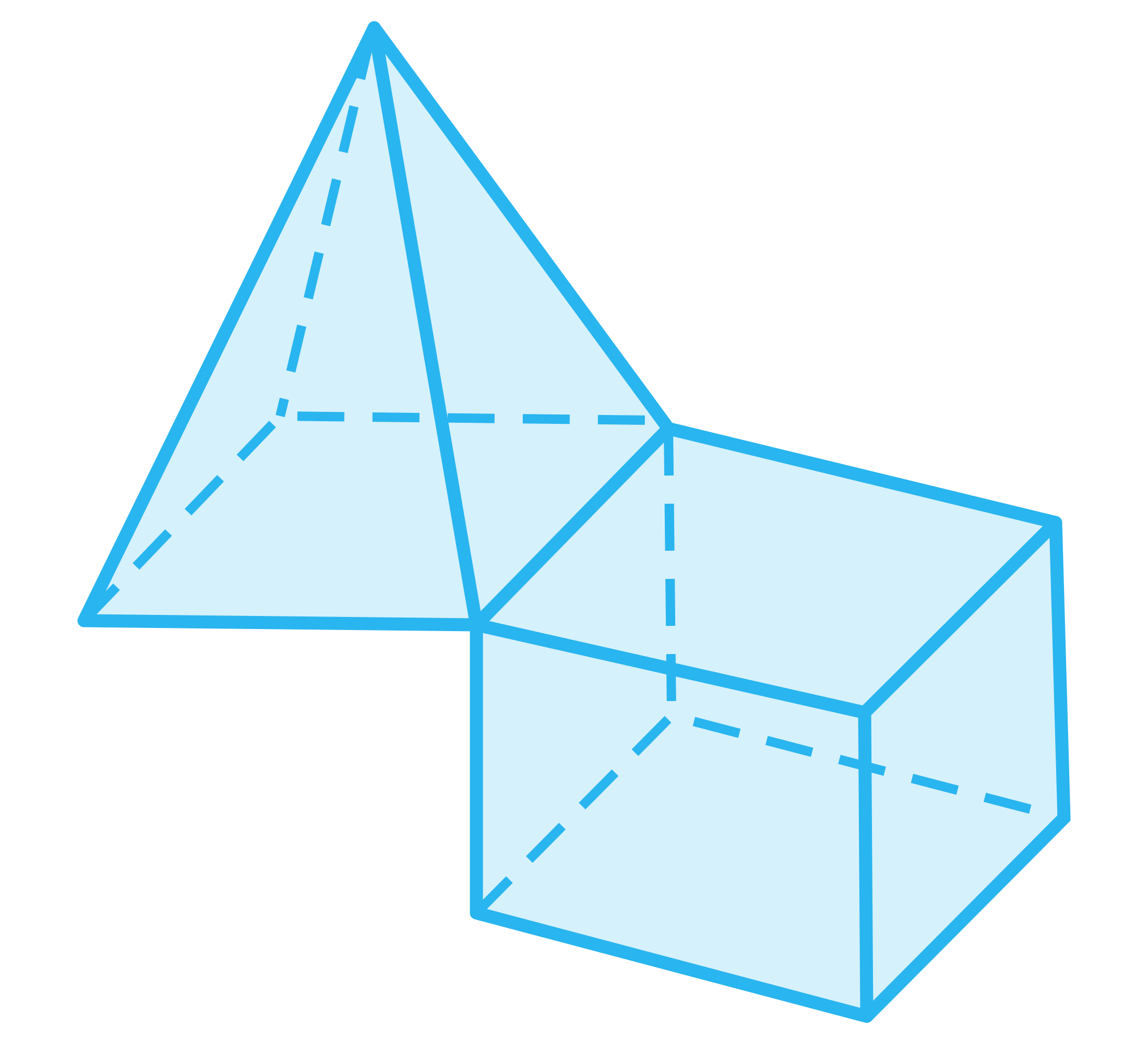

Spośród wielościanów wybierz wielościany wypukłe.
- Dwudziestościan foremny.
- Graniastosłup o podstawie trójkąta.
- Ostrosłup o podstawie kwadratu i prostopadłościan połączone identyczną krawędzią.
- Dwa czworościany połączone wierzchołkiem.
Dla danych liczb , i dobierz bryłę.
czworościan, ostrosłup trójkątny ścięty, sześcian
Zaznacz wszystkie zdania prawdziwe.
- Każdy ostrosłup spełnia twierdzenie Eulera.
- Każdy graniastosłup jest wielościanem wypukłym.
- Suma liczby wierzchołków i liczby ścian w wielościanie wypukłym jest równa liczbie krawędzi powiększonej o .
- Wielościany, które nie są wypukłe, również mogą spełniać wzór Eulera.
Wielościany foremne (platońskie) to wielościany, których ściany są przystającymi wielokątami foremnymi, a każdy wierzchołek jest wspólny dla tej samej liczby ścian. Jest to wielościan wypukły.
Uzupełnij tabelę przenosząc poprawne nazwy oraz liczby.
sześcian, , , , , ,
| nazwa | |||
|---|---|---|---|
| sześcian | |||
Sześcio-ośmiościan rombowy wielki jest wielościanem archimedesowym składającym się z kwadratów, sześciokątów i ośmiokątów. Ile wynosi , , dla tego wielościanu? Zaznacz poprawną odpowiedź. Możliwe odpowiedzi: 1. , 2. , 3. , 4.
Wielościanem archimedesowym (półforemnym) nazywamy wielościan, którego wszystkie ściany są wielokątami foremnymi różnych typów, taki, że każdy wierzchołek jest wspólny dla tej samej liczby ścian. Jest to wielościan wypukły.
Sześcio-ośmiościan rombowy wielki jest wielościanem archimedesowym składającym się z kwadratów, sześciokątów i ośmiokątów. Ile wynosi , , dla tego wielościanu? Zaznacz poprawną odpowiedź.
Sześcio–ośmiościan rombowy mały jest wielościanem półforemnym, tworzy go trójkątów równobocznych i kwadratów. Ile ścian tego wielościanu łączy się w jednym wierzchołku?
Uzasadnij, korzystając z twierdzenia Eulera, że istnieje dokładnie pięć wielościanów platońskich.
Graniastosłup i ostrosłup o tej samej podstawie sklejamy krawędzią podstawy. Uzasadnij, że tak powstała bryła, nie spełnia równości .