Sprawdź się
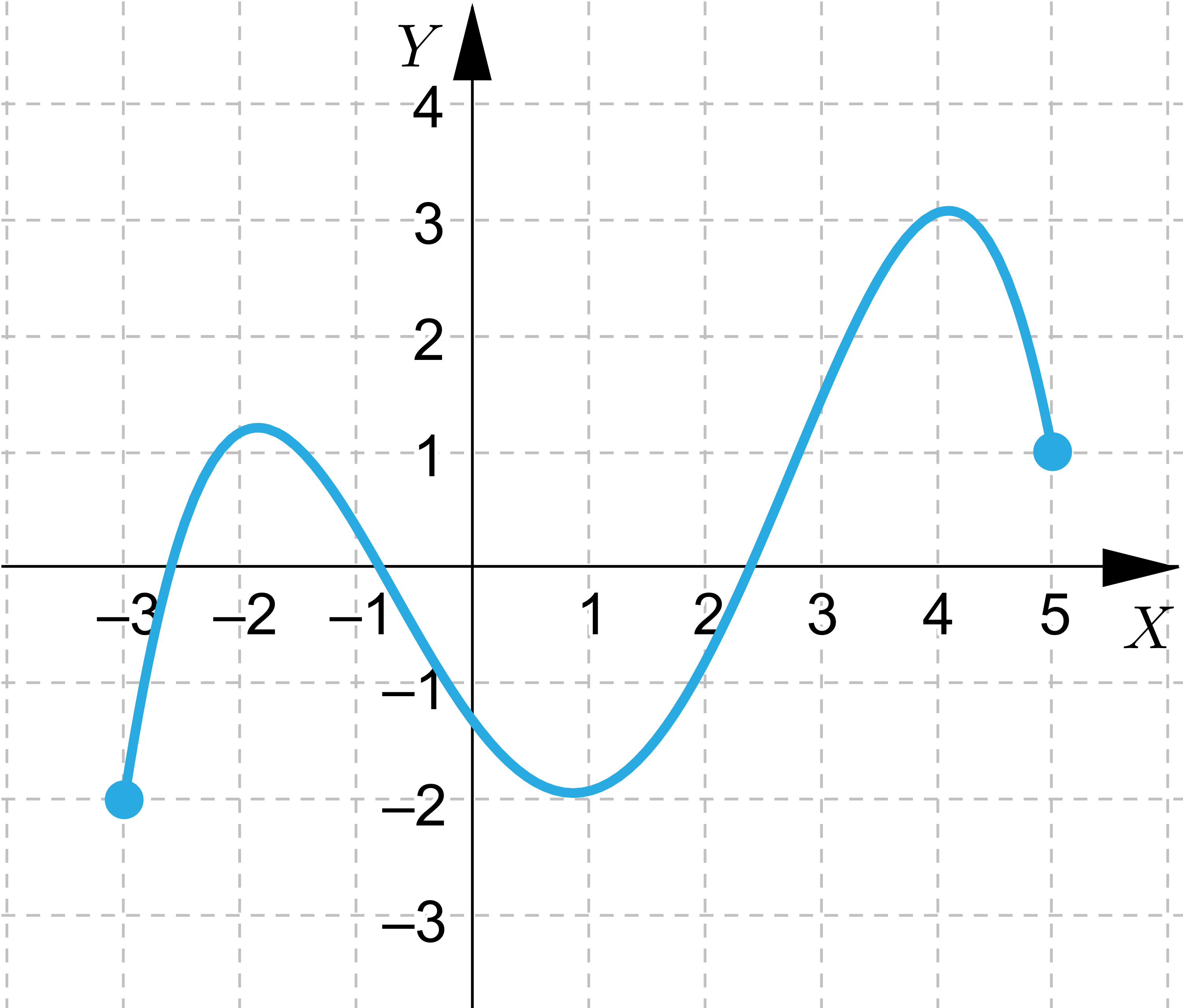
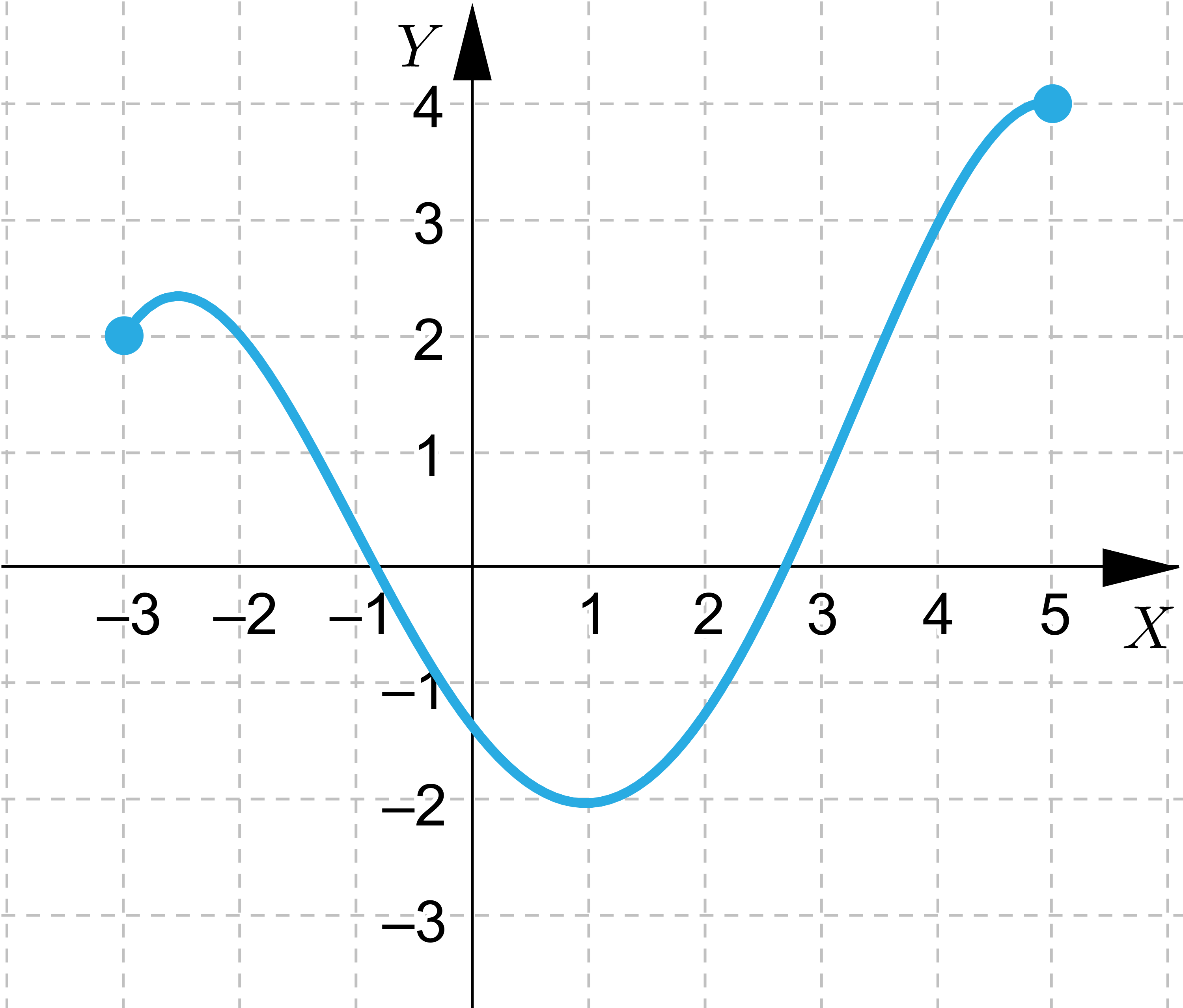
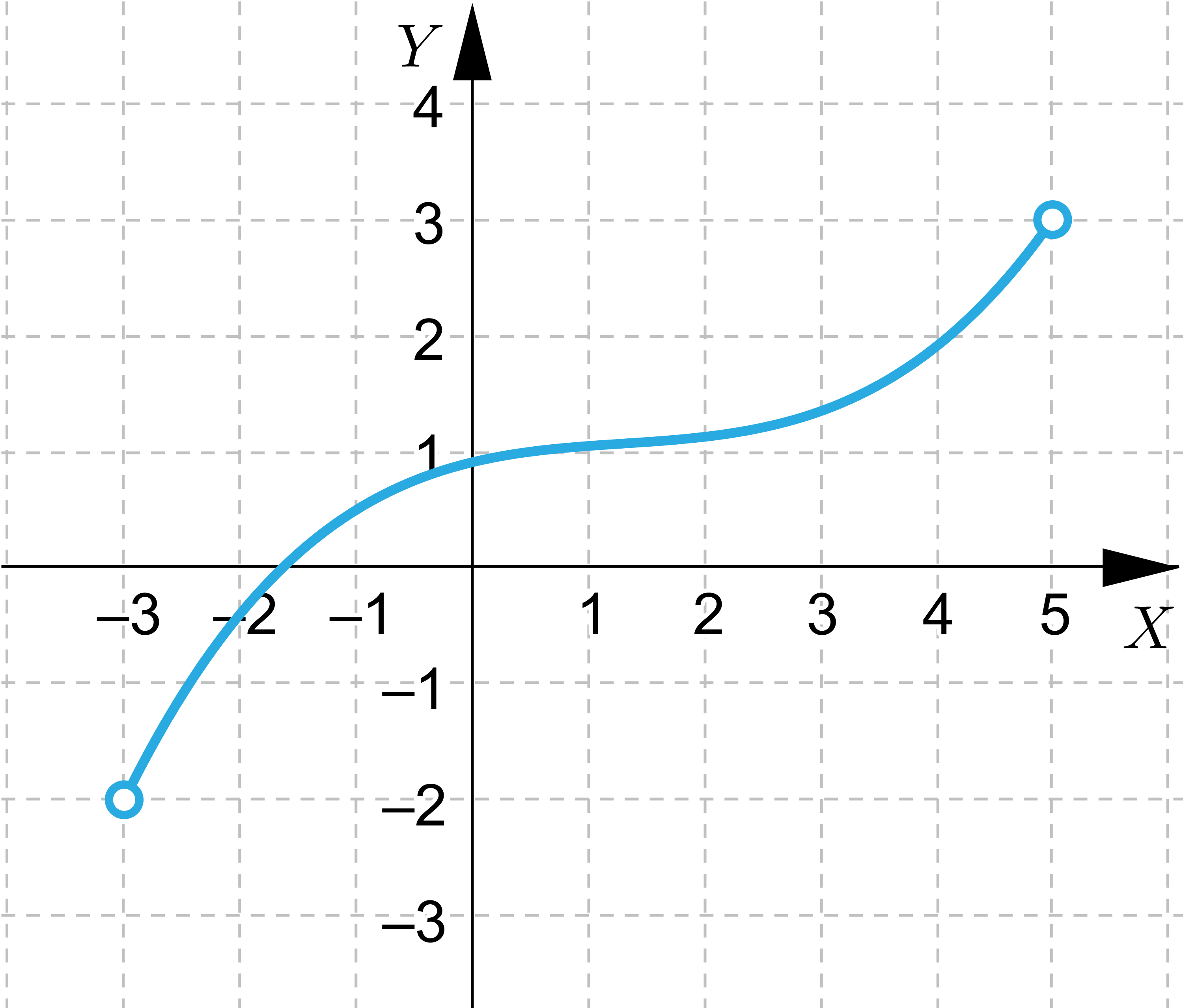
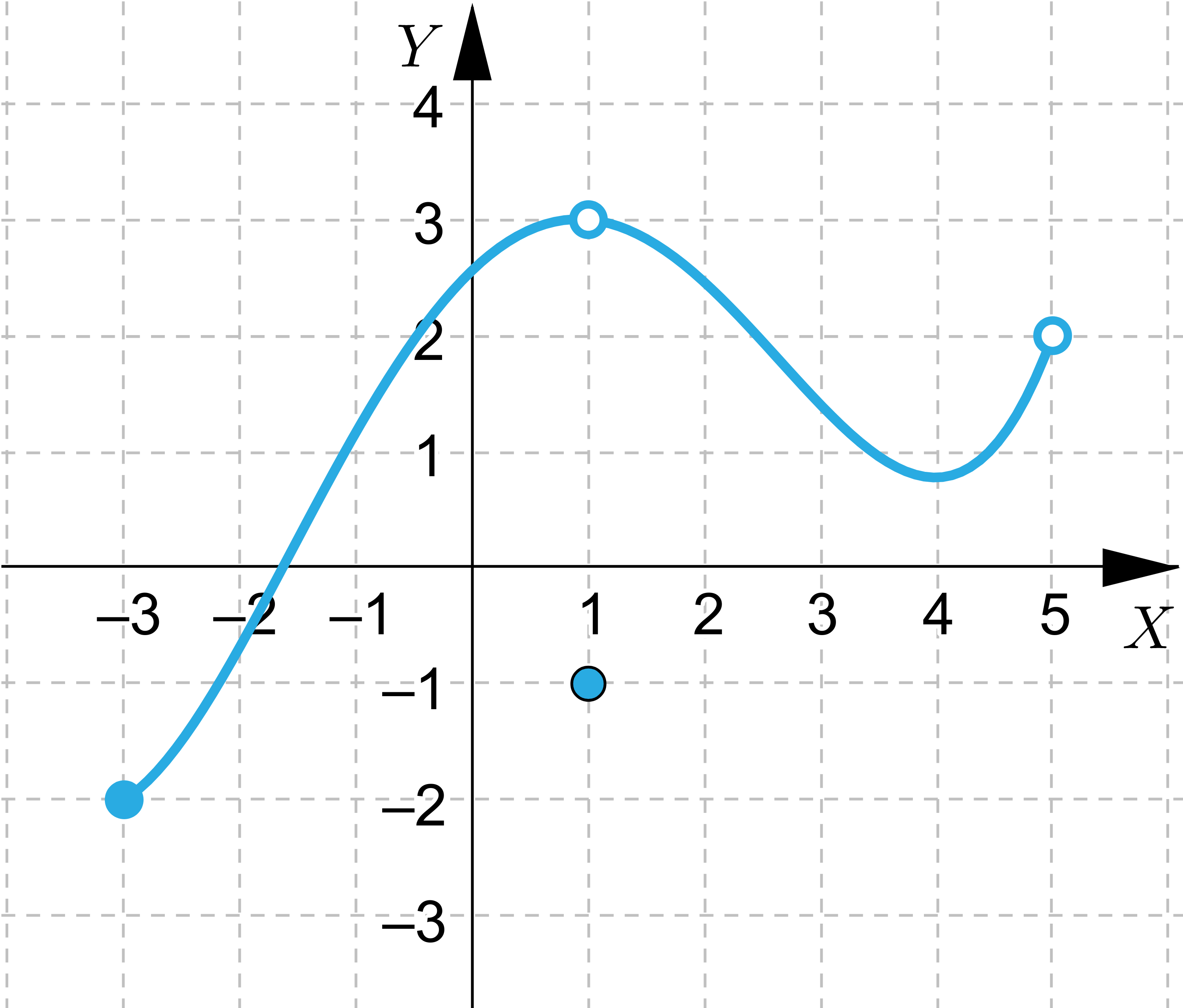
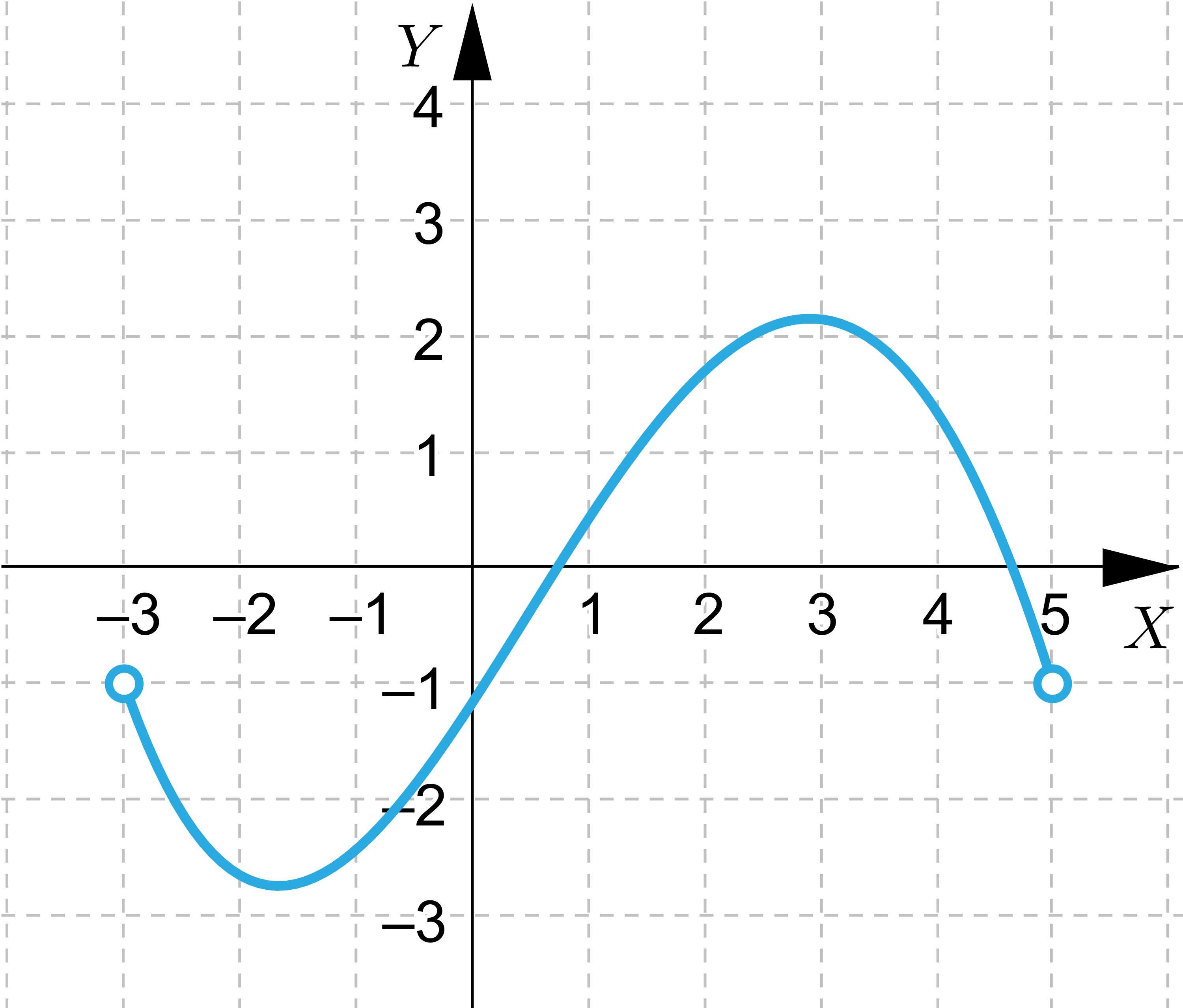
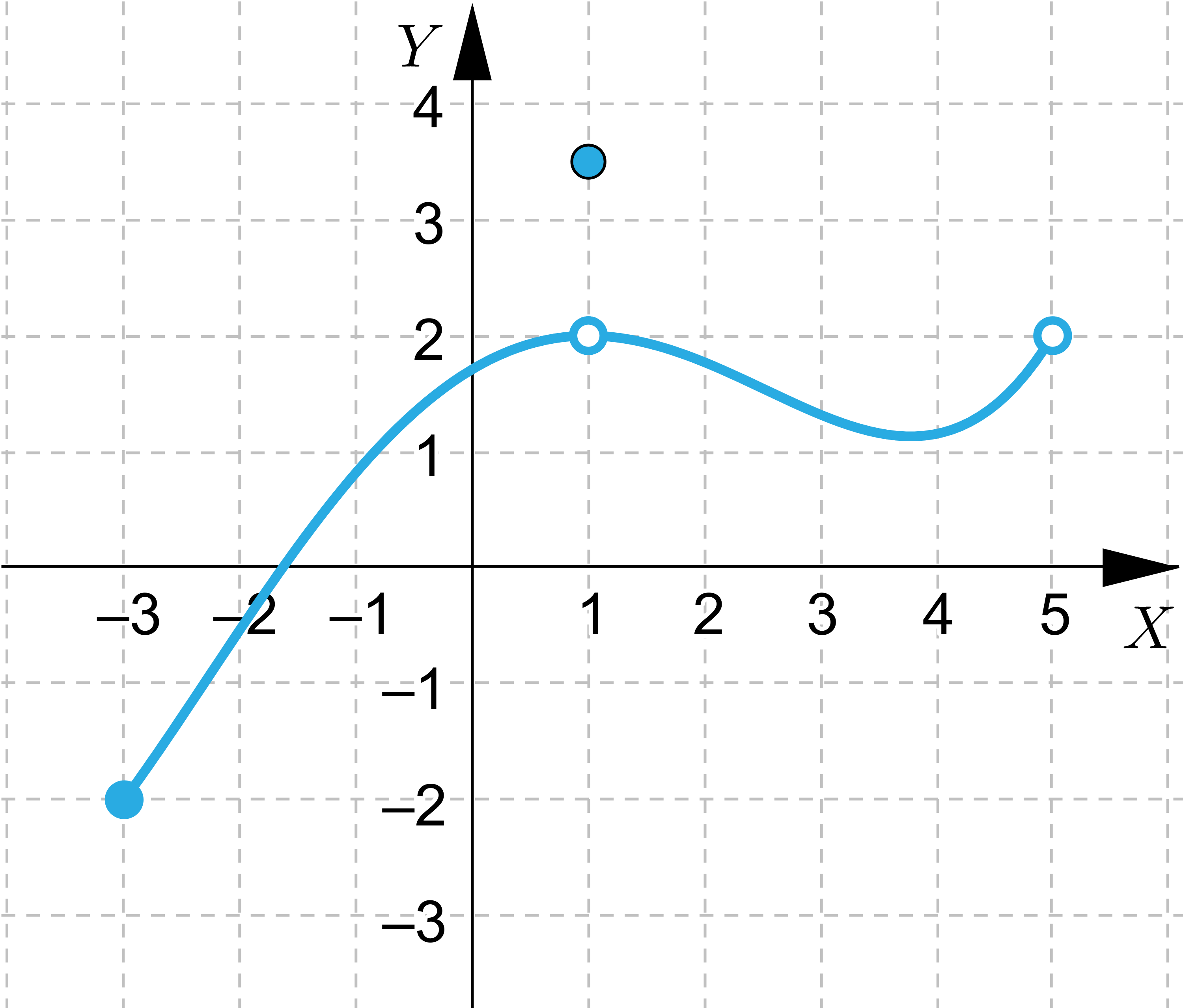
Wskaż wszystkie funkcje, które spełniają założenia Twierdzenie Weierstrassa
- A
- B
- C
- D
- E
- F
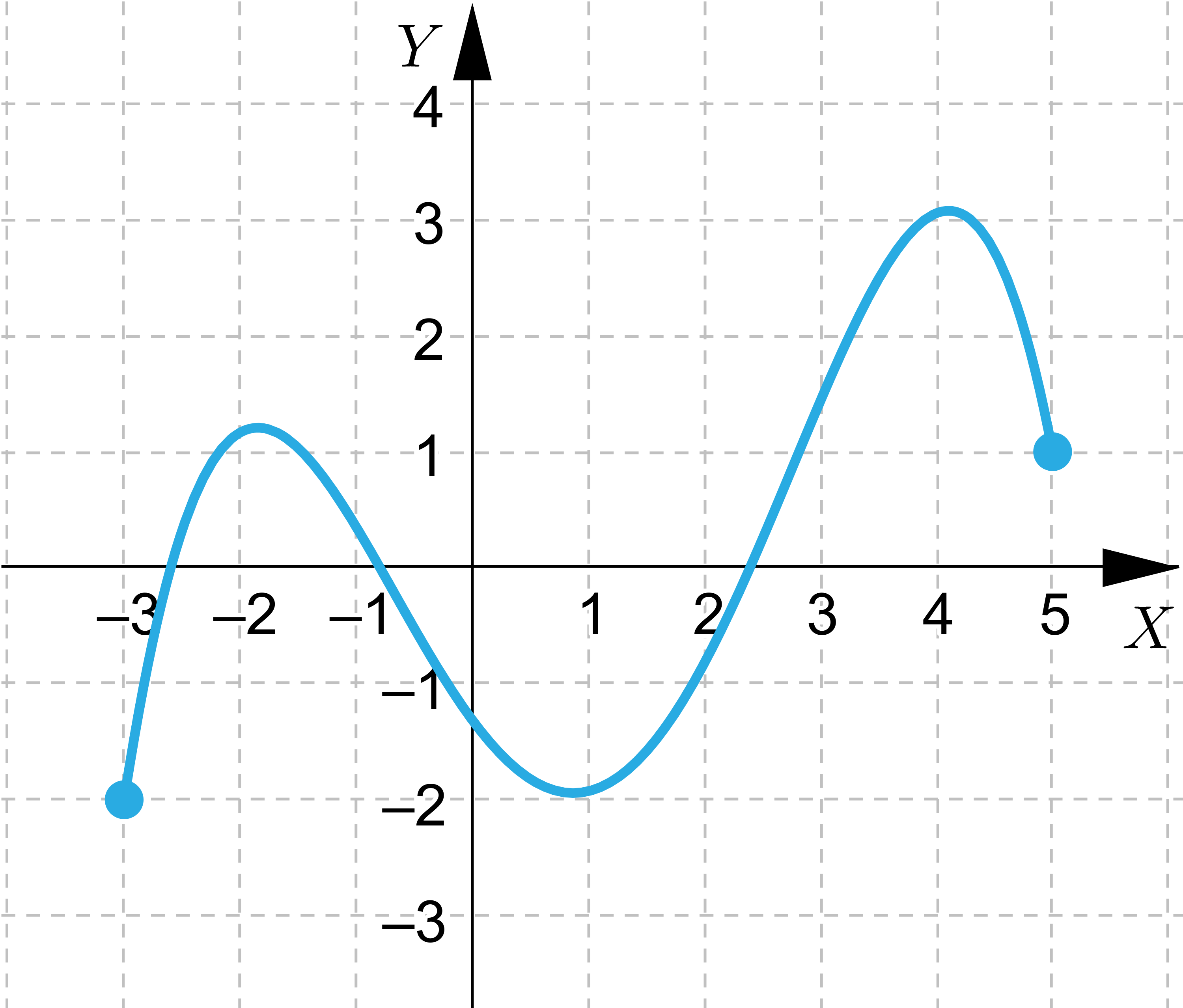
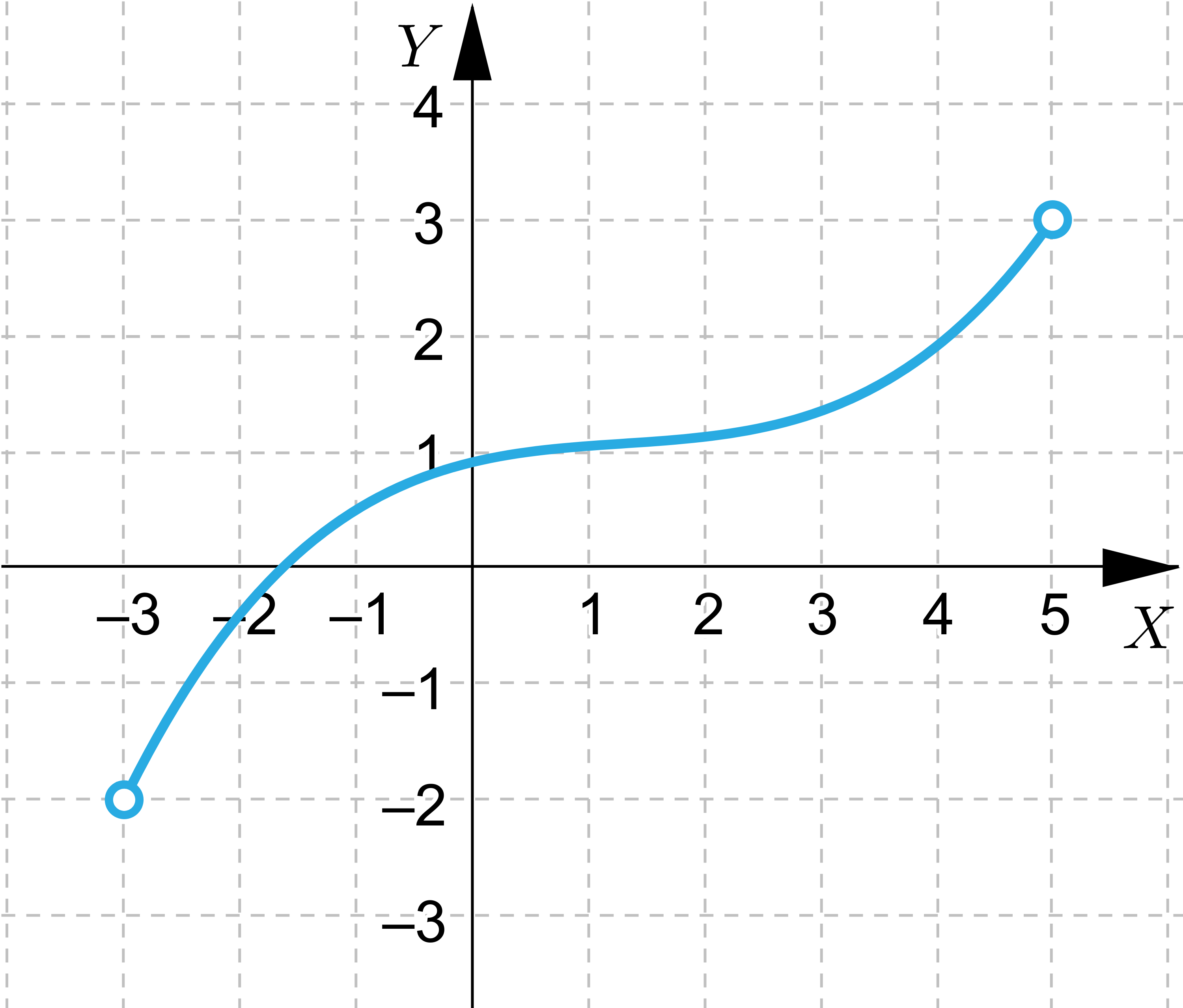
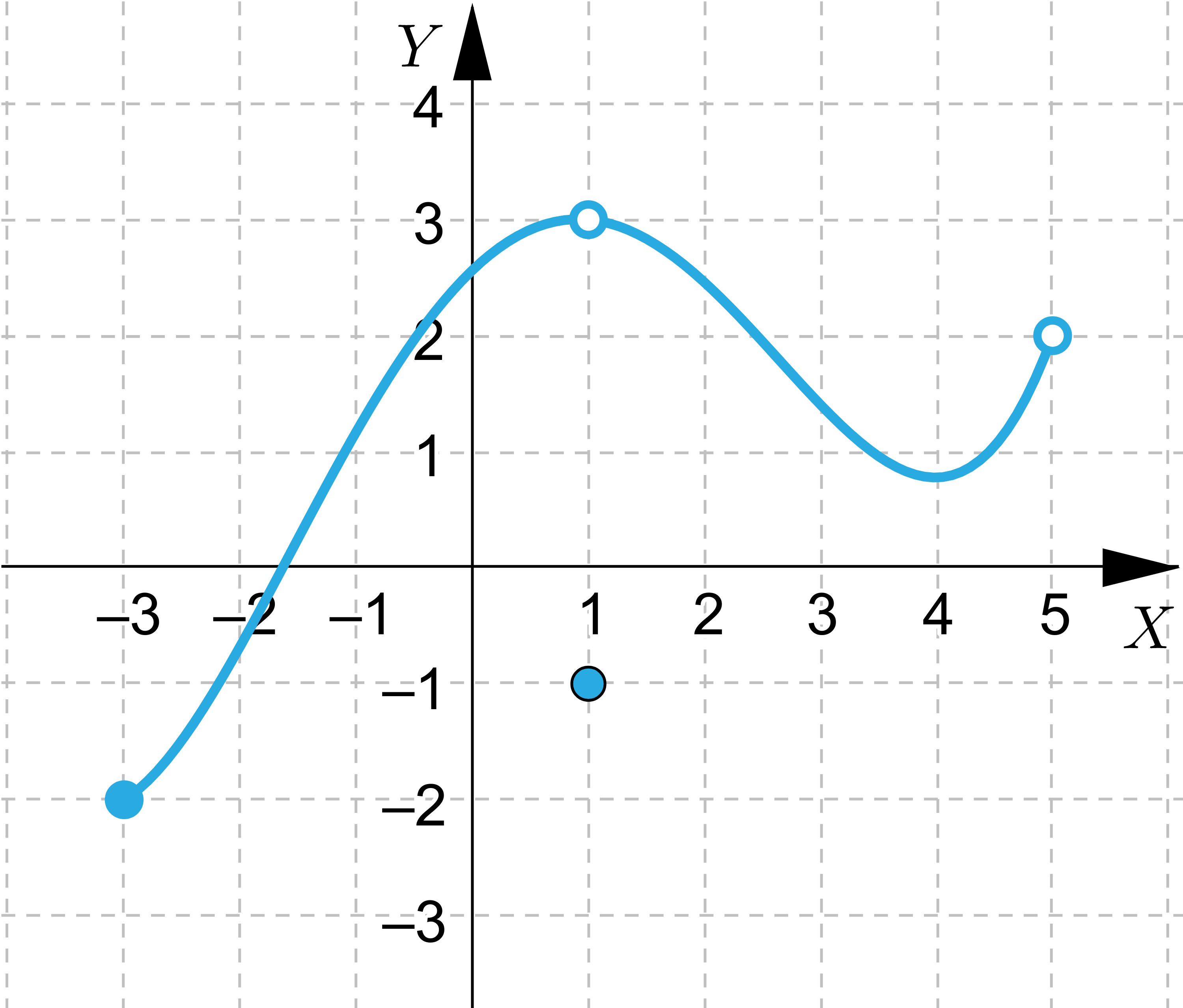
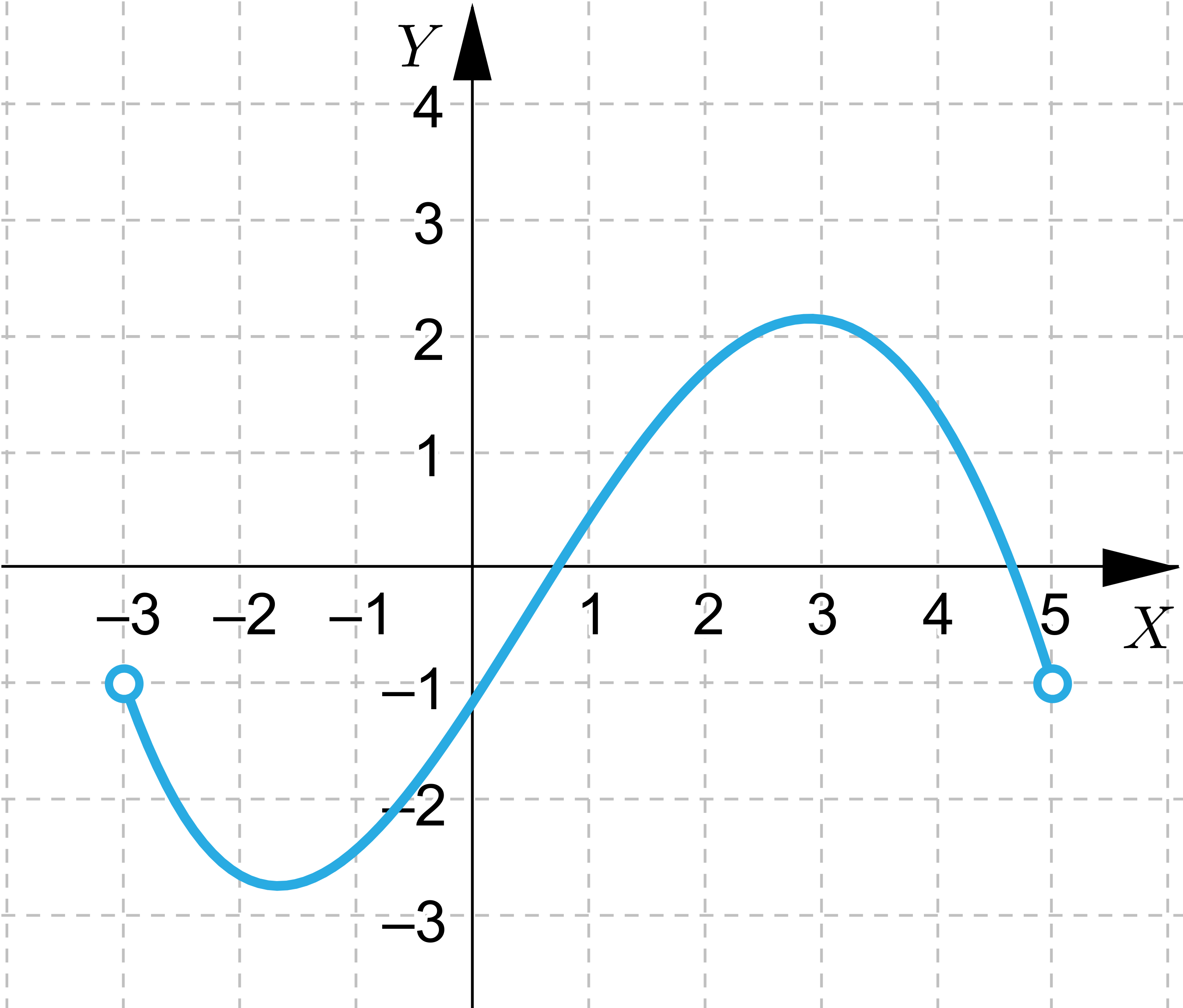
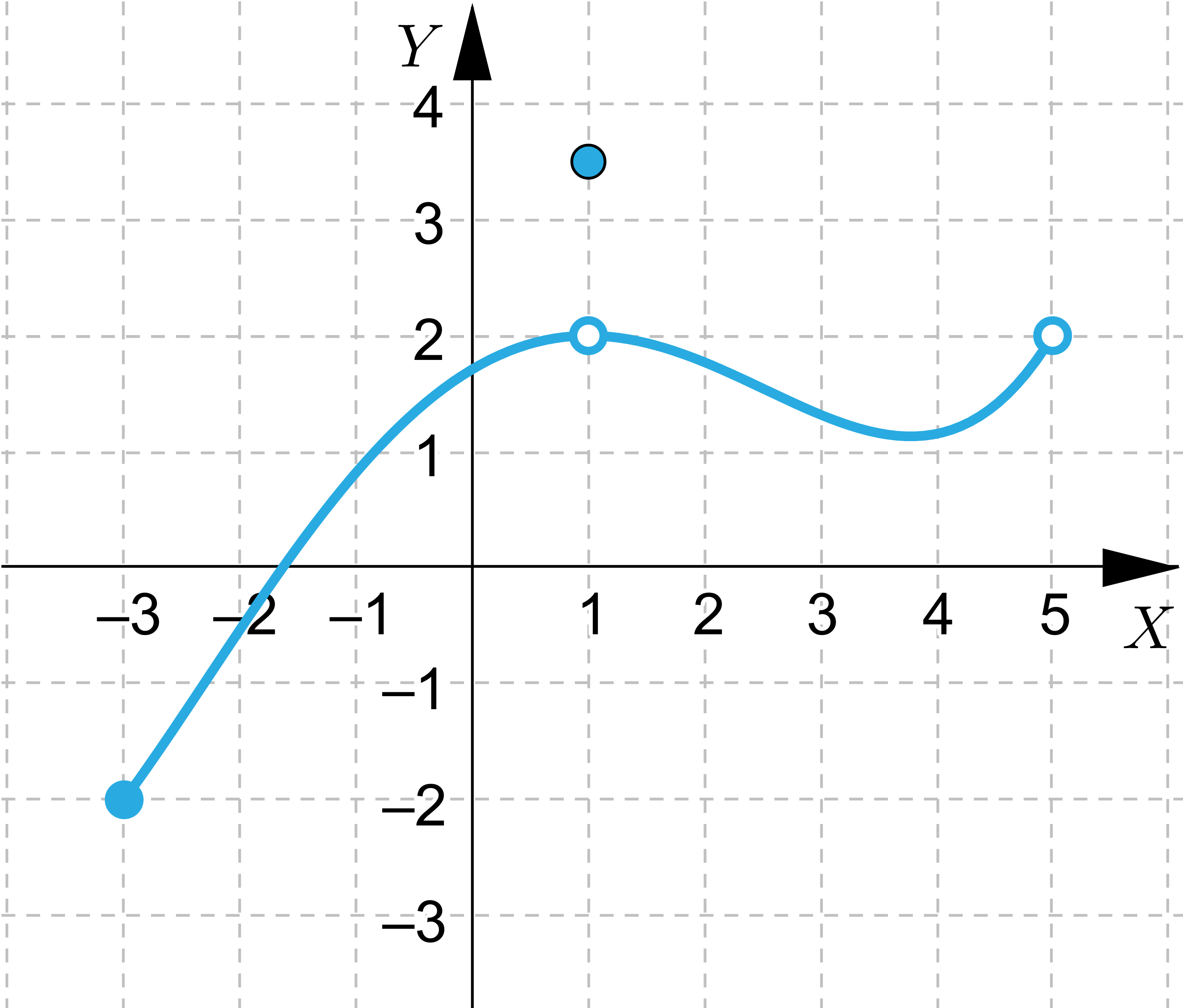
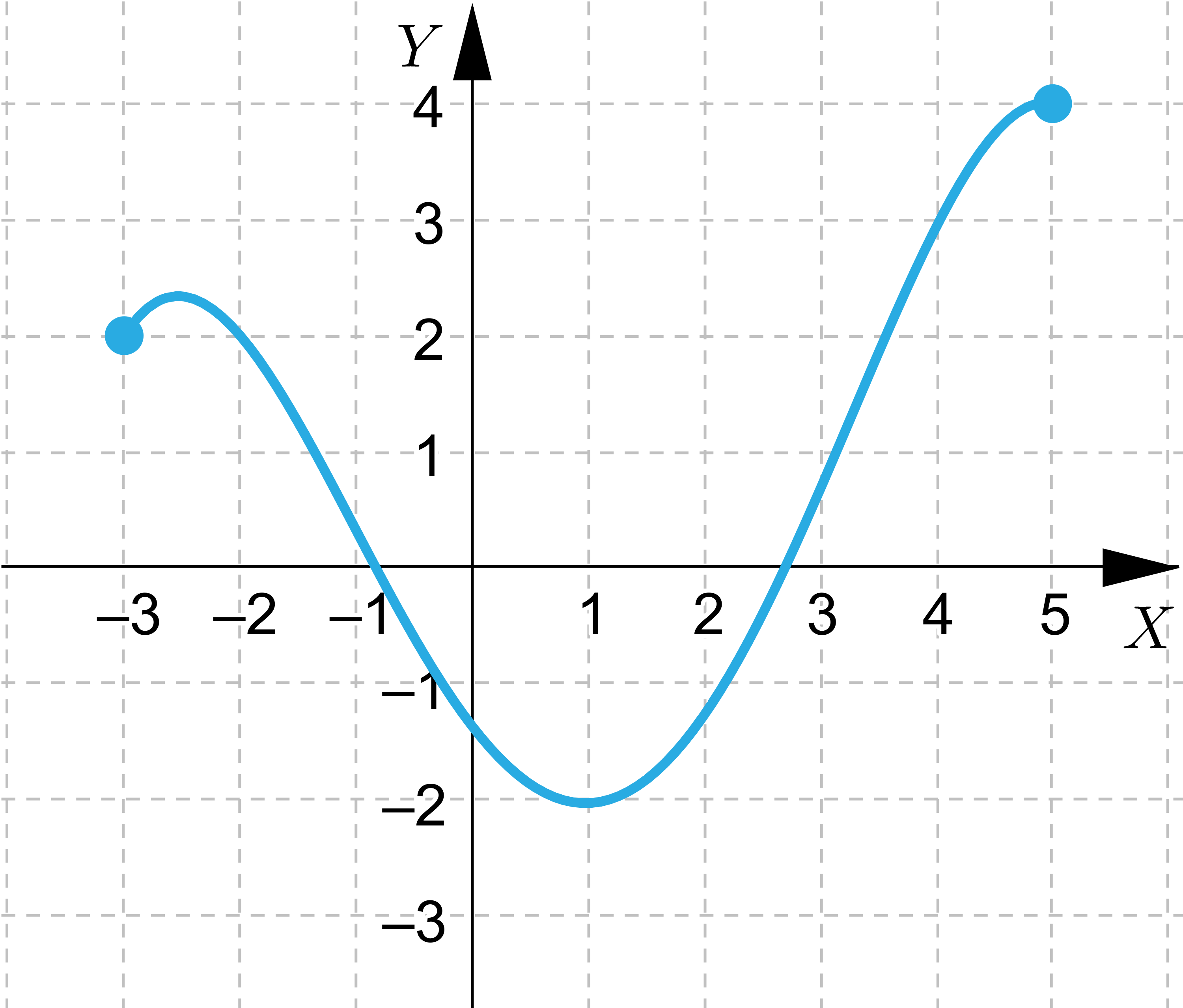
Wskaż wszystkie funkcje, które nie spełniają założeń Twierdzenie Weierstrassa, ale przyjmują wartość największą i najmniejszą.
- A
- B
- C
- D
- E
- F
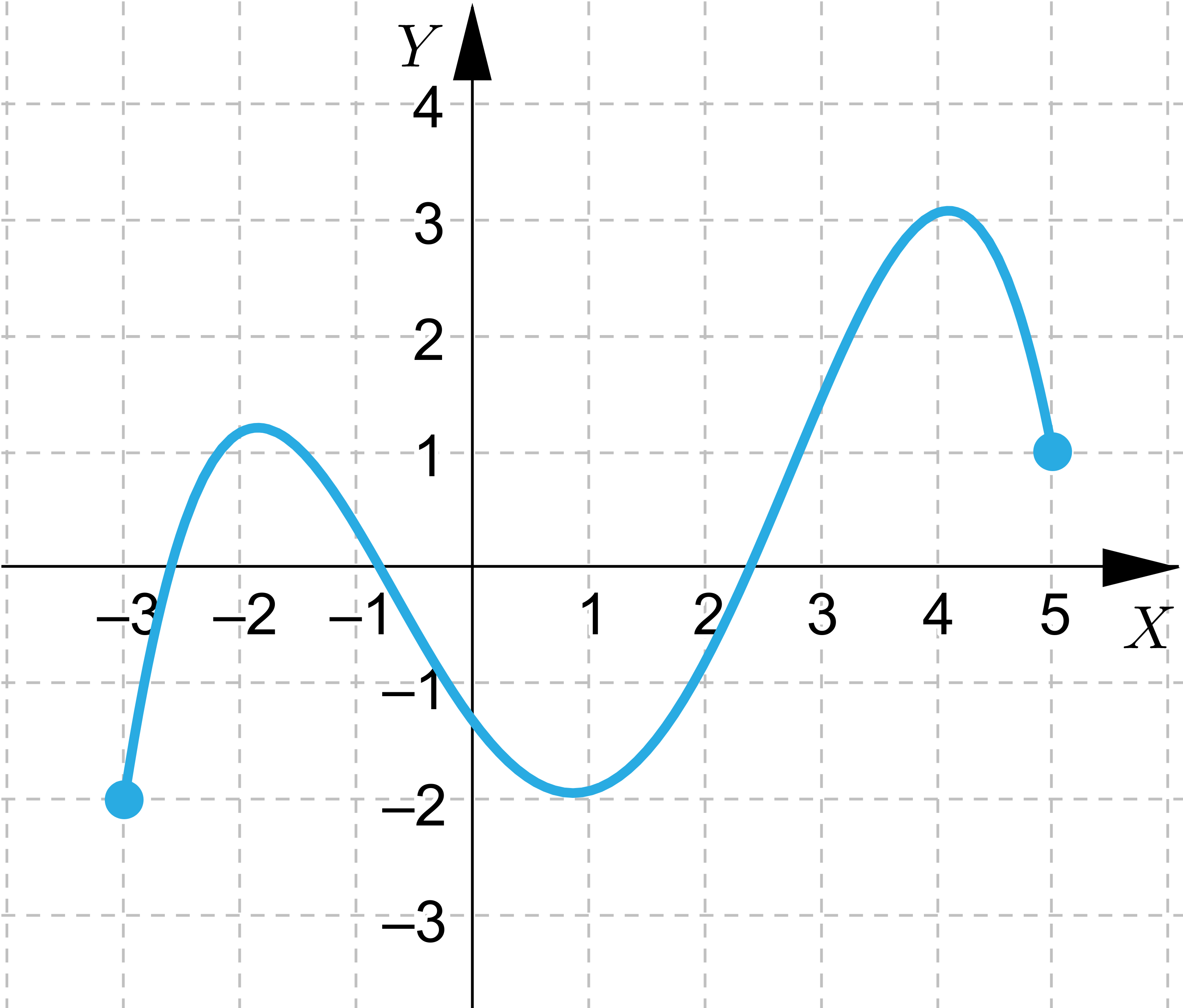
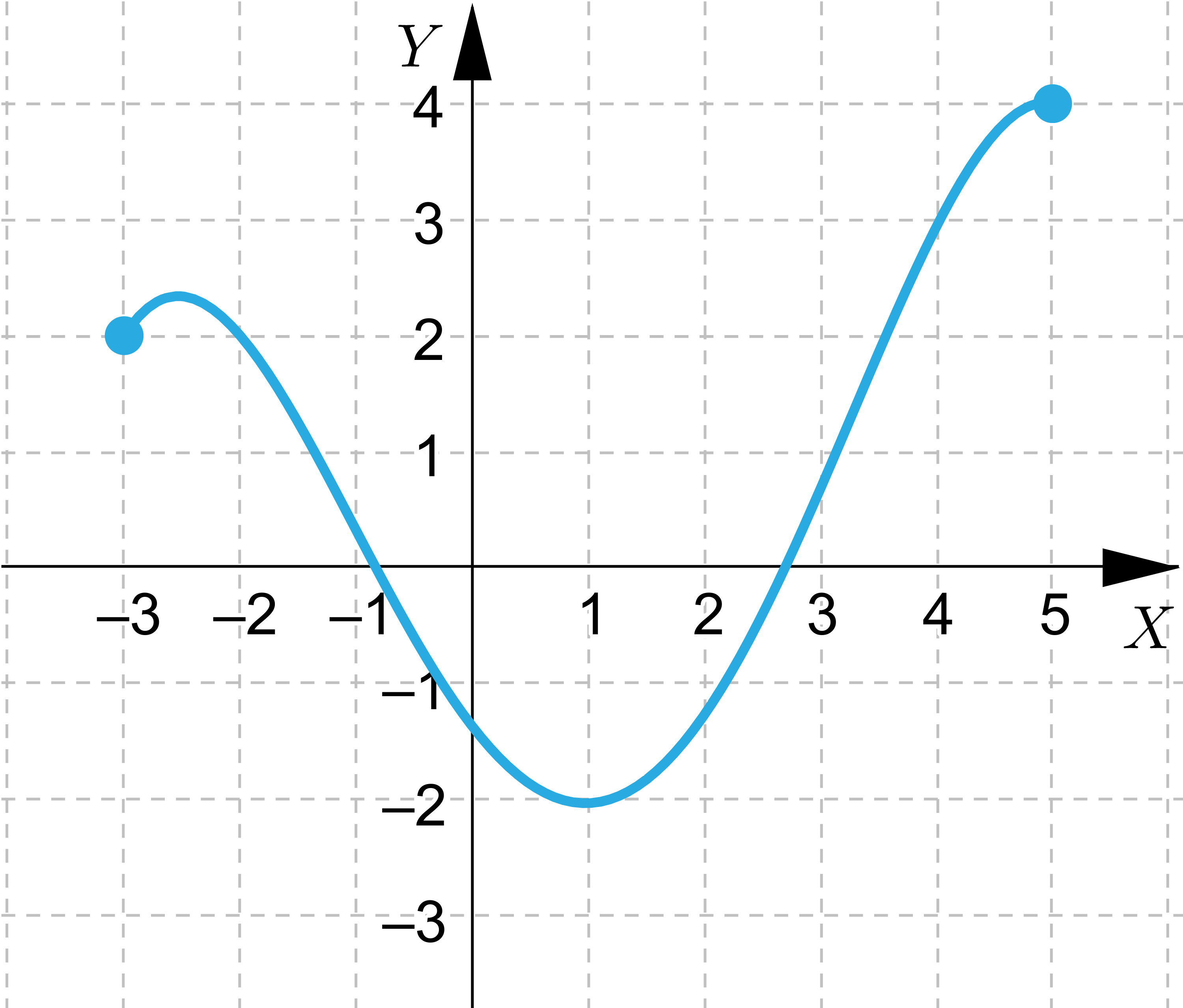
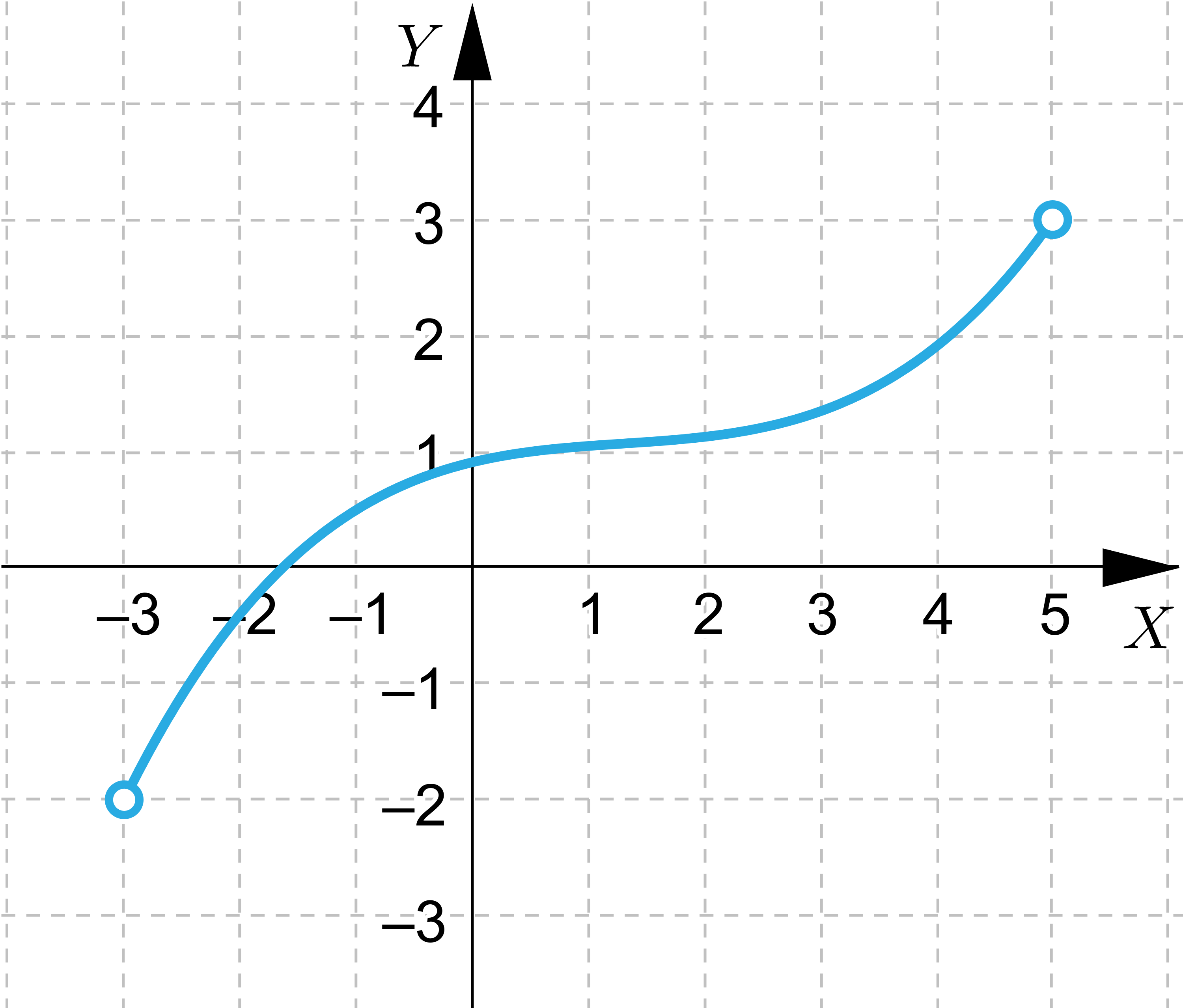
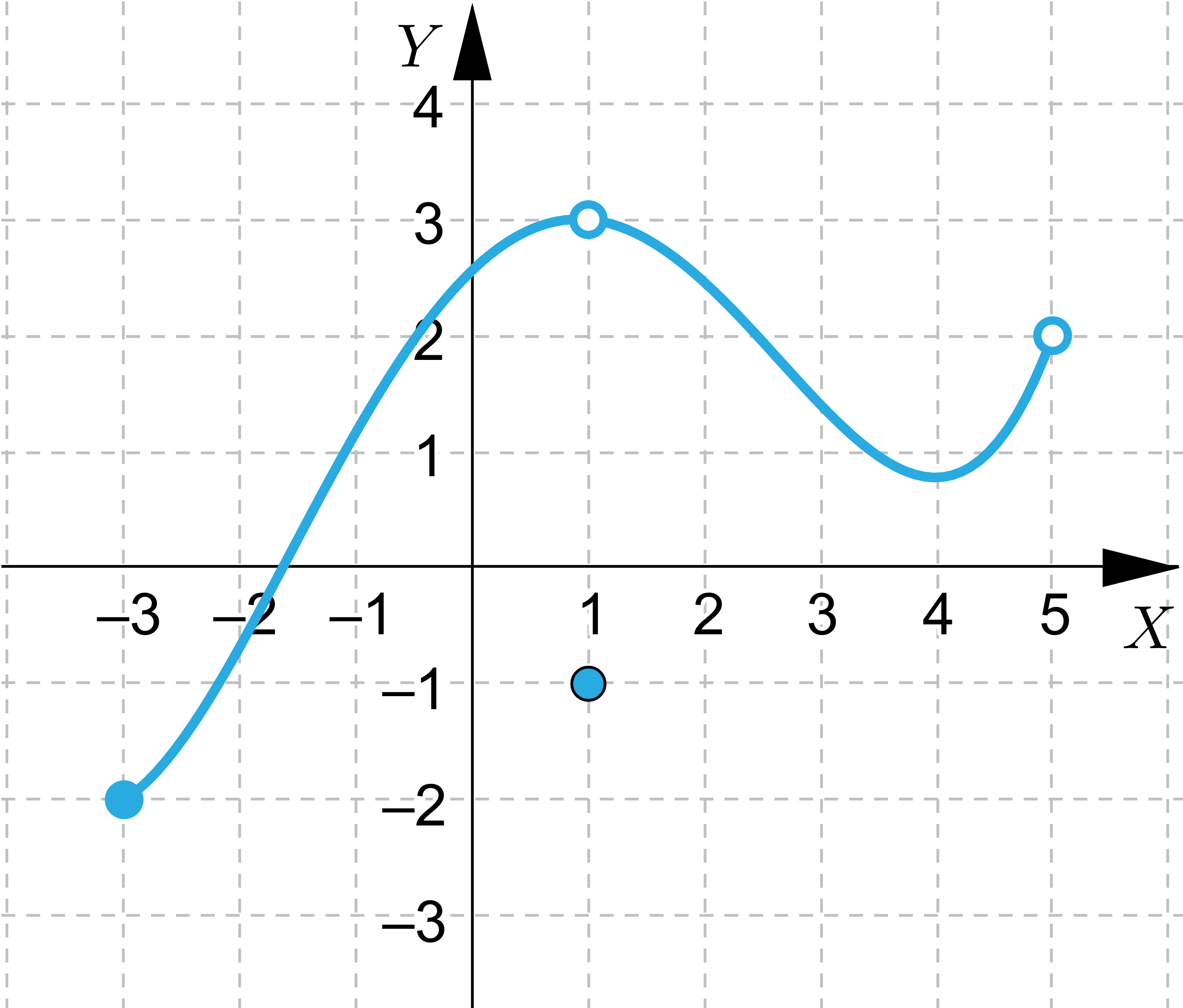
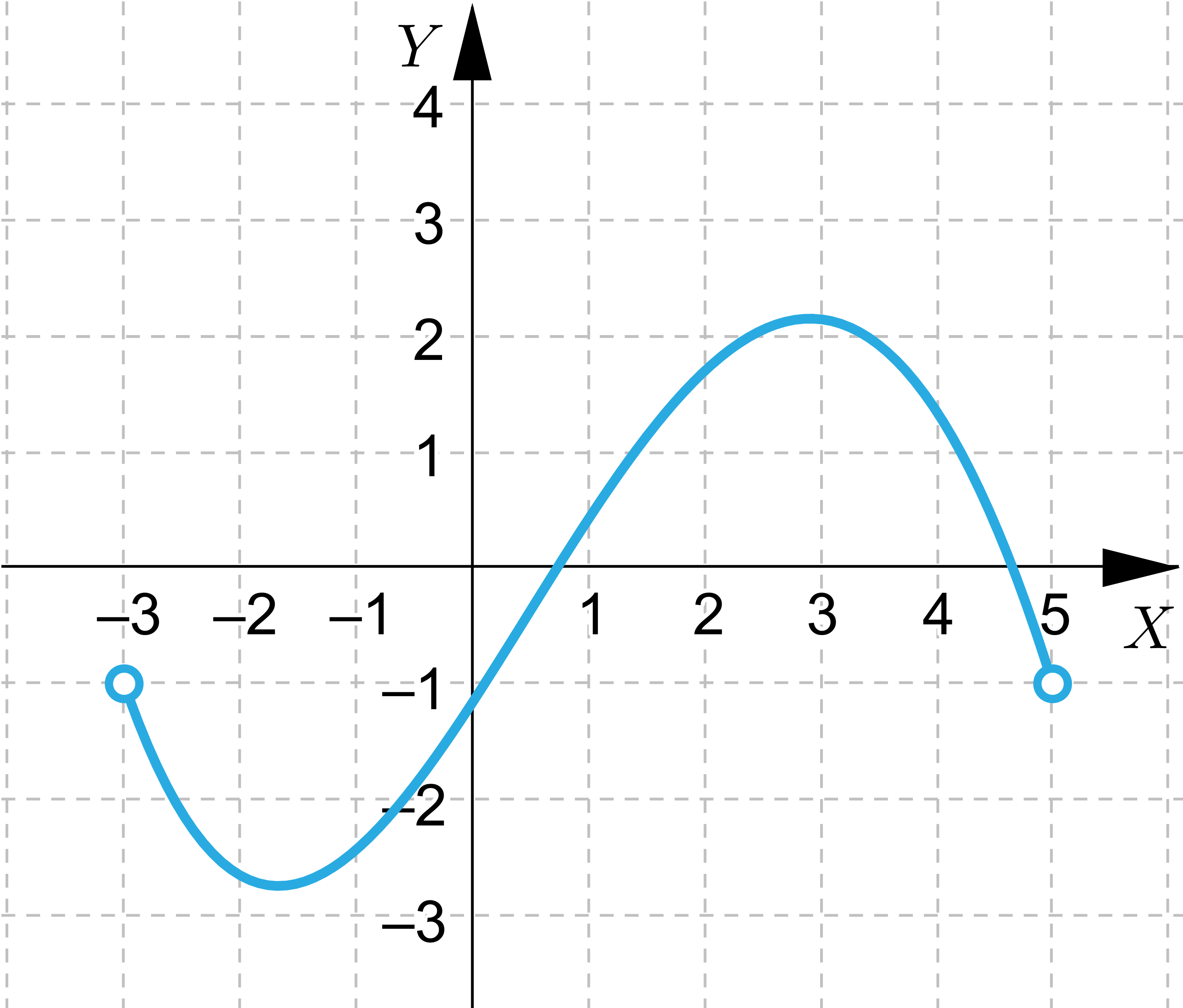
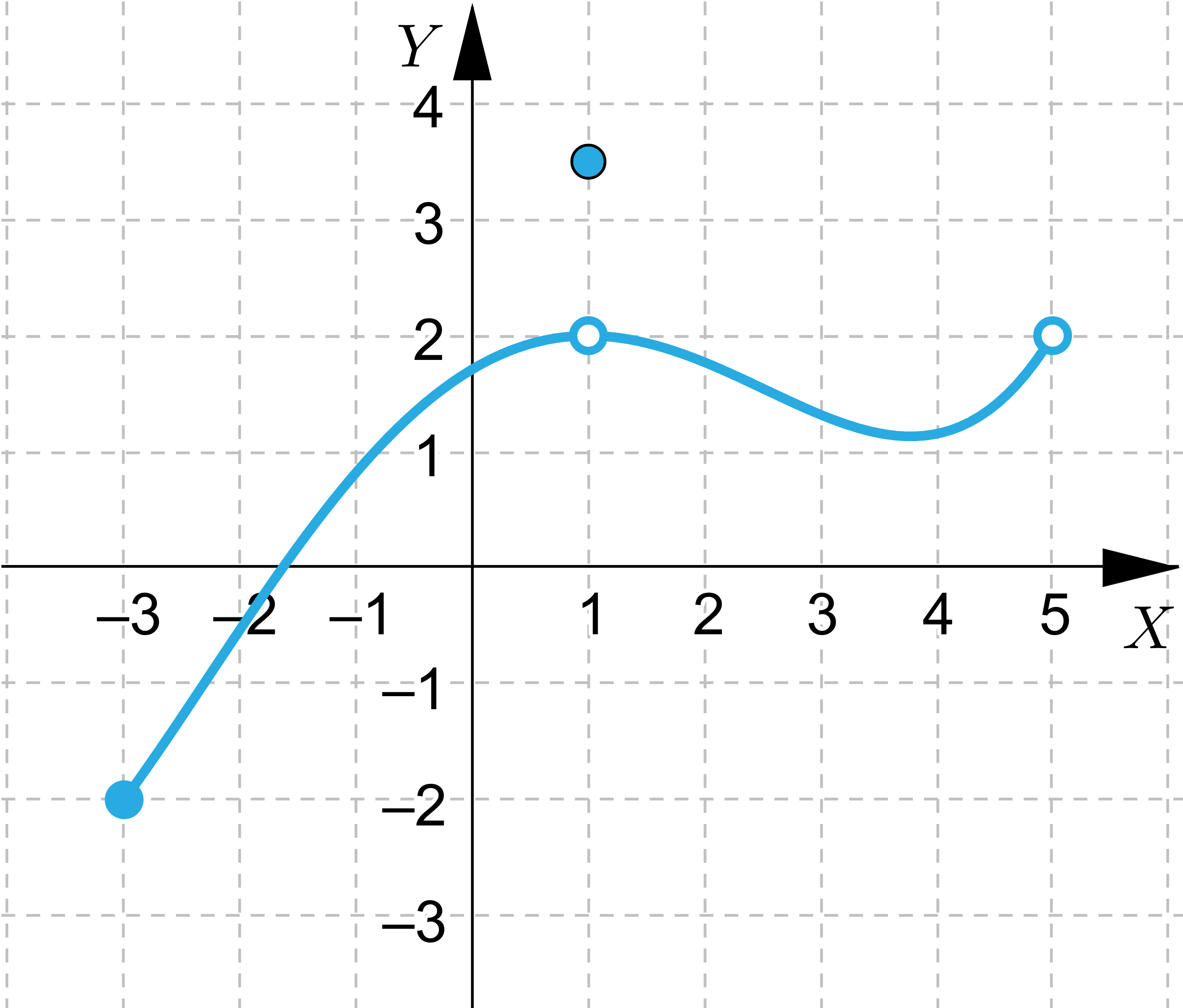
Wskaż funkcje, które nie przyjmują wartości największej lub najmniejszej.
- A
- B
- C
- D
- E
- F
-
Content: ,Next slide: Pole trójkąta wyraża się wzorem:
-
Content: ,Next slide: Pole trójkąta wyraża się wzorem:
-
Content: ,Next slide: Pamiętaj, że zgodnie z regułą trójkąta suma długości dwóch boków musi być większa niż długość trzeciego boku.
-
Content:Next slide: Bez straty ogólności możemy szukać wartości najmniejszej wyrażenia . Jego pochodna wyraża się wzorem:
-
Content:Next slide: Bardzo ładnie wyłączyłeś czynnik przed nawias. Musisz jednak uważać na znaki: .
-
Content:Next slide: Bez straty ogólności możemy szukać wartości najmniejszej wyrażenia . Jego pochodna wyraża się wzorem:
-
Content:Next slide: W tym zadaniu nie możemy dowolnie zamieniać zmiennych, bo wiemy, że to podstawa trójkąta.
-
Content: Wróć na poprzedni slajd.Next slide: Rozważmy trójkąt równoramienny o podstawie , ramionach i obwodzie równym . Wybierz jedną z podanych sytuacji i odpowiedz na następne pytania.
-
Content:Next slide: Miejsce zerowe pochodnej, które należy do dziedziny funkcji to:
-
Content:Next slide: Masz dobrą intuicję, że można wyłączyć przed nawias. Pamiętaj, że dzielić możesz obie strony równania a nie wzór funkcji.
-
Content:Next slide: Miejsce zerowe pochodnej, które należy do dziedziny funkcji to:
-
Content:Next slide: Masz dobrą intuicję, że można wyłączyć przed nawias. Pamiętaj, że dzielić możesz obie strony równania, ale nie wzór funkcji.
-
Content:Next slide: Oczywiście ani , ani nie należą do dziedziny rozważanej funkcji (nie da się zbudować trójkąta o boku , nie da się zbudować trójkąta z odcinków długości , , ). Zauważ, że gdybyśmy mimo to wstawili te wielkości do wyprowadzonych wzoru na pole trójkąta, to otrzymalibyśmy , które możemy interpretować jako pole odcinka.
Zatem, skoro rozważamy ciągłą funkcję o wartościach nieujemnych, w punkcie osiągana jest wartość największa funkcji! Zauważ, że jeśli jeden z boków ma długość , to rozważany trójkąt jest trójkątem równobocznym. -
Content:Next slide: Zauważ, że ani , ani nie należą do dziedziny rozważanej funkcji. Dziedzinę określaliśmy na początku naszej drogi. Zresztą, w każdej chwili możemy to sprawdzić – nie da się zbudować trójkąta o boku , nie da się zbudować trójkąta z odcinków długości , , .
-
Content:Next slide: Zauważ, że ani , ani nie należą do dziedziny rozważanej funkcji. Dziedzinę określaliśmy na początku naszej drogi. Zresztą, w każdej chwili możemy to sprawdzić – nie da się zbudować trójkąta o boku , nie da się zbudować trójkąta z odcinków długości , , .
-
Content: Dziękujemy. Spróbuj przyjść tu inną drogą.Next slide: Rozważmy trójkąt równoramienny o podstawie , ramionach i obwodzie równym . Wybierz jedną z podanych sytuacji i odpowiedz na następne pytania.
-
Content: Wróć na poprzedni slajd.Next slide: Pole trójkąta wyraża się wzorem:
-
Content: Wróć na poprzedni slajd.Next slide: Pole trójkąta wyraża się wzorem:
-
Content: Wróć na poprzedni slajd.Next slide: Miejsce zerowe pochodnej, które należy do dziedziny funkcji to:
-
Content: WróćNext slide: Miejsce zerowe pochodnej, które należy do dziedziny funkcji to:
-
Content: Wróć na poprzedni slajd.Next slide: Bez straty ogólności możemy szukać wartości najmniejszej wyrażenia . Jego pochodna wyraża się wzorem:
Zatem, skoro rozważamy ciągłą funkcję o wartościach nieujemnych, w punkcie osiągana jest wartość największa funkcji! Zauważ, że jeśli jeden z boków ma długość , to rozważany trójkąt jest trójkątem równobocznym.
Wzrost cen o , , powoduje spadek liczby klientów o .
a.
b.
Rozważmy funkcję daną wzorem .
Ustal jak, w zależności od wartości parametru , zmieniają się wartości największa i najmniejsza funkcji .
<span aria-label="f indeks dolny, m i n, koniec indeksu dolnego" role="math"><math><msub><mi>f</mi><mrow><mi>m</mi><mi>i</mi><mi>n</mi></mrow></msub></math></span> nie istnieje, <span aria-label="f indeks dolny, m a x, koniec indeksu dolnego, równa się, a" role="math"><math><msub><mi>f</mi><mrow><mi>m</mi><mi>a</mi><mi>x</mi></mrow></msub><mo>=</mo><mi>a</mi></math></span>, <span aria-label="f indeks dolny, m i n, koniec indeksu dolnego, równa się, a" role="math"><math><msub><mi>f</mi><mrow><mi>m</mi><mi>i</mi><mi>n</mi></mrow></msub><mo>=</mo><mi>a</mi></math></span>, <span aria-label="f indeks dolny, m a x, koniec indeksu dolnego, równa się, jeden" role="math"><math><msub><mi>f</mi><mrow><mi>m</mi><mi>a</mi><mi>x</mi></mrow></msub><mo>=</mo><mn>1</mn></math></span>, <span aria-label="f indeks dolny, m i n, koniec indeksu dolnego" role="math"><math><msub><mi>f</mi><mrow><mi>m</mi><mi>i</mi><mi>n</mi></mrow></msub></math></span> nie istnieje, <span aria-label="f indeks dolny, m a x, koniec indeksu dolnego, równa się, jeden" role="math"><math><msub><mi>f</mi><mrow><mi>m</mi><mi>a</mi><mi>x</mi></mrow></msub><mo>=</mo><mn>1</mn></math></span>
Rozważmy funkcję daną wzorem .
Spośród podanych zbiorów wskaż te, dla których , .
Na poniższym rysunku przedstawiono fragment wykresu funkcji . W poniższej tabeli przedstawiono wartość największą i najmniejszą tej funkcji w zależności od przyjętej dziedziny. Uzupełnij tabelę przeciągając właściwe odpowiedzi we wskazane miejsce.
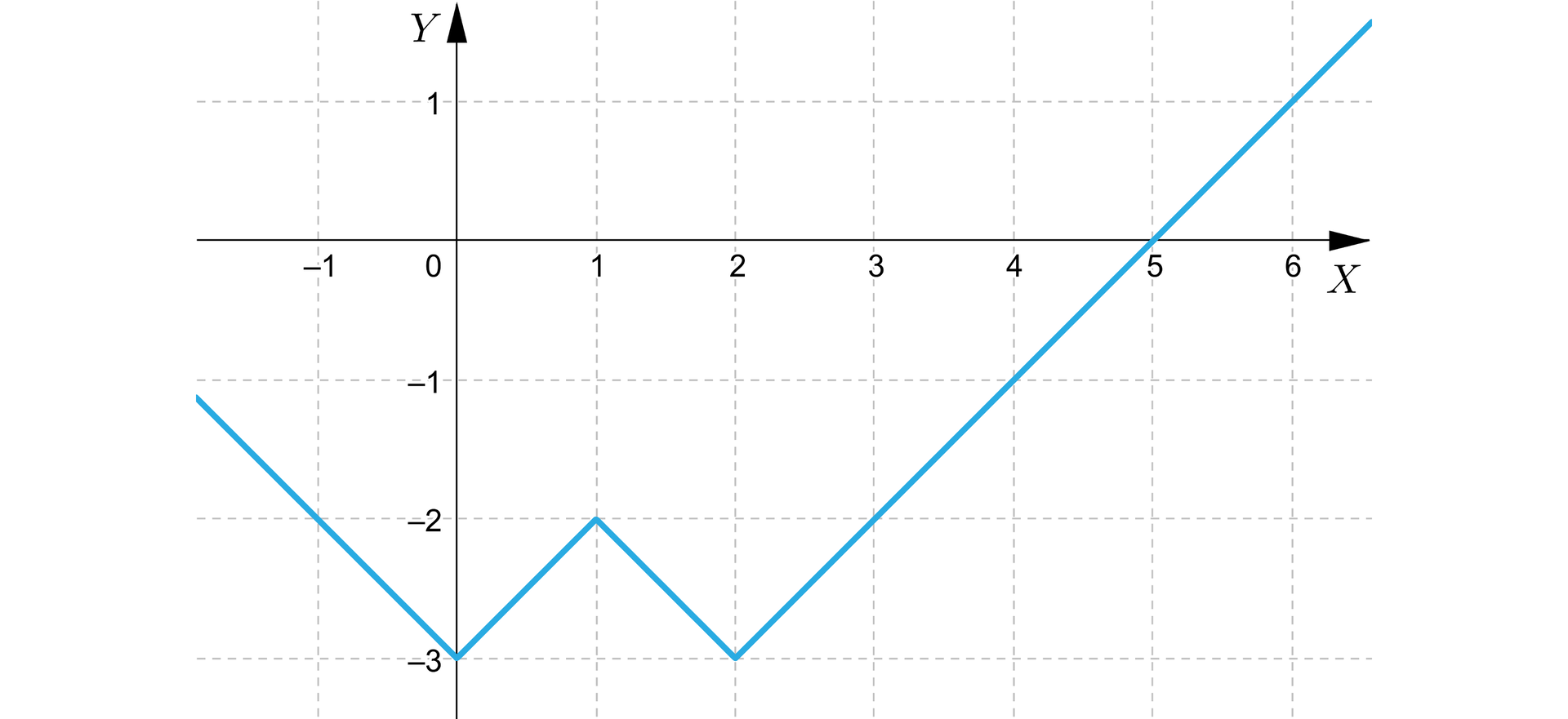
, , , ,
| Dziedzina | ||
|---|---|---|