Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

Na rysunku przedstawiono sześcian $A B C D E F G H$ .

RAg9LD6cKRijE

Grafika przedstawia sześcian, którego wierzchołki dolnej podstawy opisano A, B, C, D, a wierzchołki górnej podstawy opisano: E, F, G, H. Wierzchołki B, D, F, H tworzą płaszczyznę, której krawędziami są przekątne podstaw i krawędzie ścian bocznych.

R1GigVlrvdWMc

Zaznacz poprawną odpowiedź. Prostą równoległą do płaszczyzny $D B F H$ jest:

$F B$
$E G$
$C D$

Ćwiczenie 2

Na rysunku przedstawiono prostopadłościan $A B C D E F G H$ .

R1AshlqzZ85MN

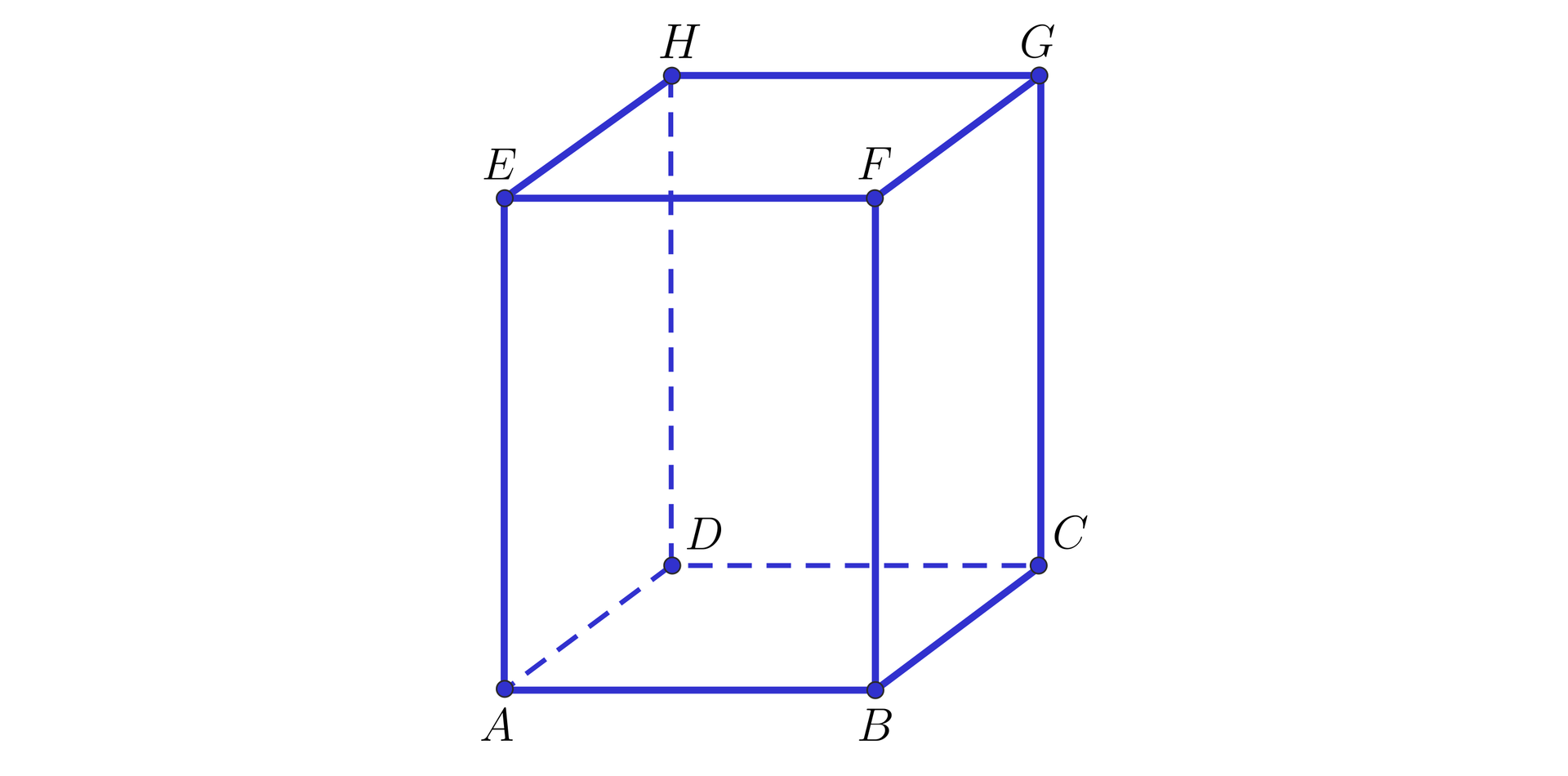
Grafika przedstawia prostopadłościan, którego wierzchołki dolnej podstawy opisano A, B, C, D, a wierzchołki górnej podstawy opisano: E, F, G, H.

RpRglXL75D43P

Zaznacz wszystkie zdania, które są prawdziwe.

Prosta $B D$ jest równoległa do płaszczyzn $A B C D$ i $E F G H$ .
Każda prosta równoległa do płaszczyzny $D C G H$ jest równoległa do płaszczyzny $B C G F$ .
Istnieją tylko dwie proste, które są równoległe do płaszczyzny $A B C D$ .
Każda prosta zawarta w płaszczyźnie $A D H E$ jest równoległa do płaszczyzny $B C F G$ .

Ćwiczenie 3

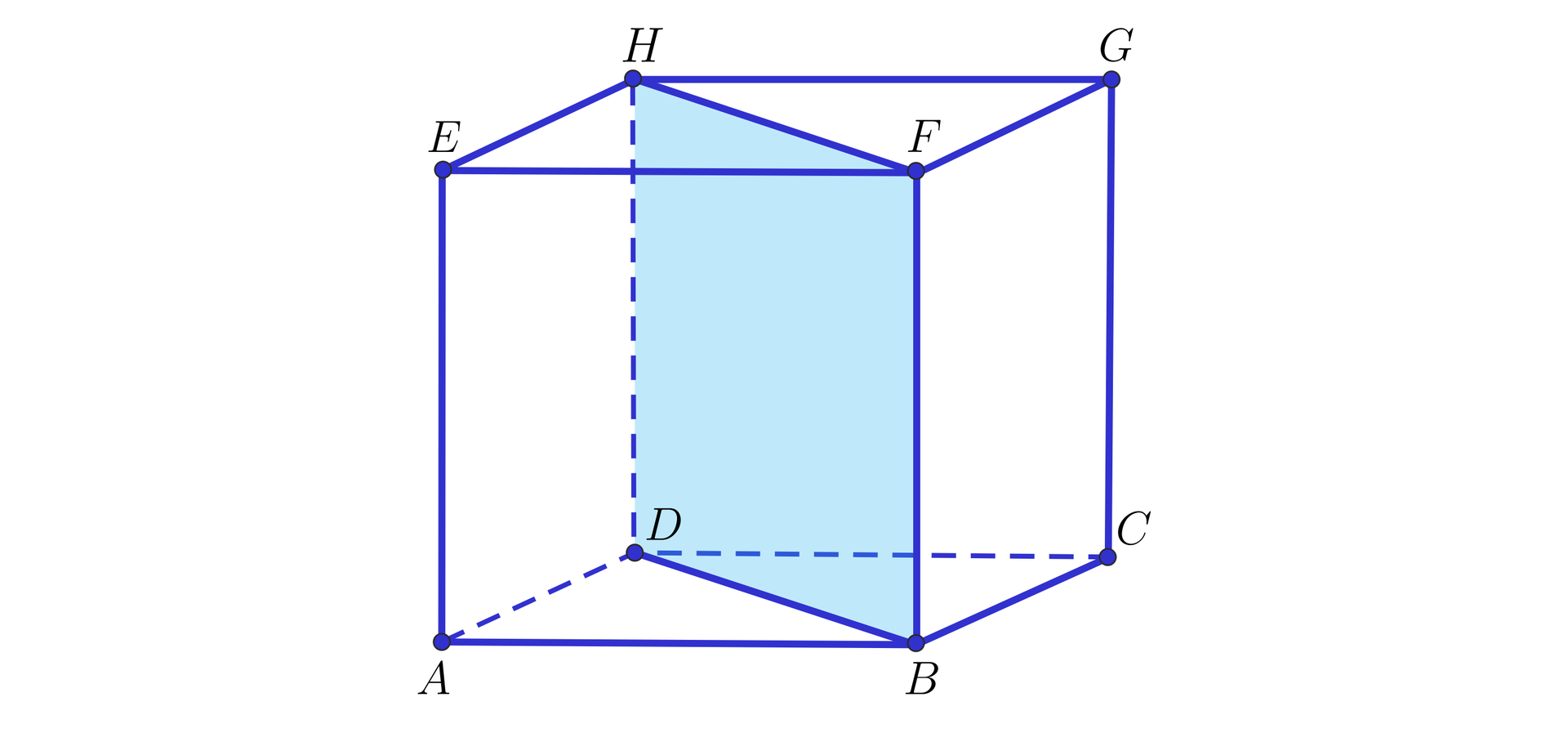
Na rysunku przedstawiono graniastosłup prawidłowy trójkątny.

RNMMwq3Rzt5cD

Grafika przedstawia graniastosłup prawidłowy trójkątny, którego wierzchołki dolnej podstawy opisano A, B, C, a wierzchołki górnej podstawy opisano: D, E, F.

R1QFGy7zhbnx1

Połącz w pary prostą z płaszczyzną do której ta prosta jest równoległa, pod warunkiem, że prosta nie zawiera się w tej płaszczyźnie.

$A C$
$E F$
$A D$
$C F$

Ćwiczenie 4

Na rysunku przedstawiono graniastosłup prawidłowy sześciokątny, którego wszystkie krawędzie mają długość $6$ .

RUkAPlF6GKy05

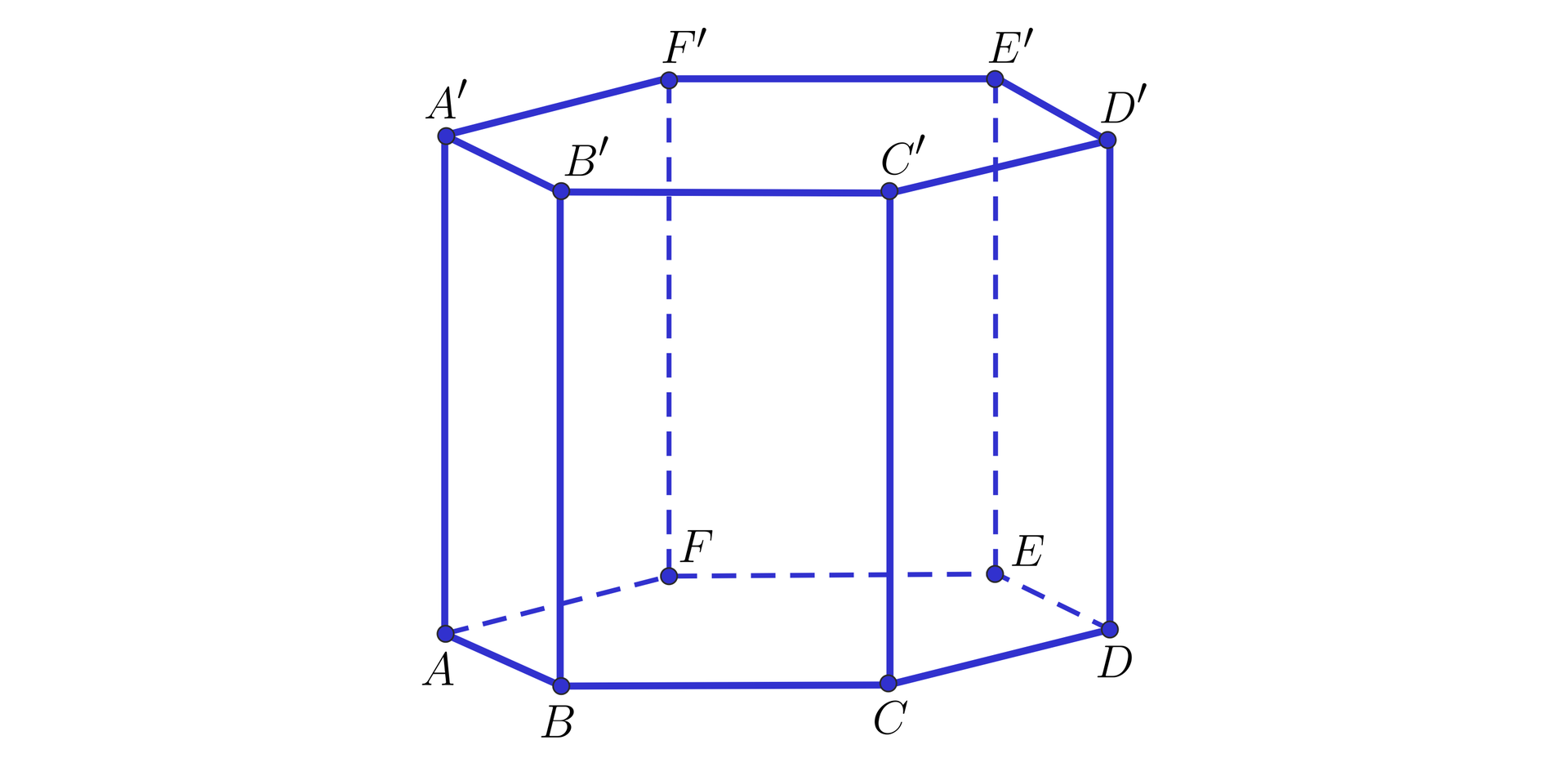
Grafika przedstawia graniastosłup prawidłowy sześciokątny, którego wierzchołki dolnej podstawy opisano A, B, C, D, E, F a wierzchołki górnej podstawy opisano: A', B', C', D', E', F'.

R1E9ZbC4H4f8Q

Wstaw w tekst odpowiednie liczby.

Odległość prostej $D D'$ od płaszczyzny $A F F' A'$ wynosi 1. $6$ , 2. $12$ , 3. $6 \sqrt{3}$ , 4. $3 \sqrt{3}$ , 5. $12 \sqrt{3}$ , 6. $0$ .
Odległość prostej $E E'$ od płaszczyzny $C D D' C'$ wynosi 1. $6$ , 2. $12$ , 3. $6 \sqrt{3}$ , 4. $3 \sqrt{3}$ , 5. $12 \sqrt{3}$ , 6. $0$ .
Odległość prostej $F F'$ od płaszczyzny $A F F' A'$ wynosi 1. $6$ , 2. $12$ , 3. $6 \sqrt{3}$ , 4. $3 \sqrt{3}$ , 5. $12 \sqrt{3}$ , 6. $0$ .
Odległość prostej $A' B'$ od płaszczyzny $A B C D E F$ wynosi 1. $6$ , 2. $12$ , 3. $6 \sqrt{3}$ , 4. $3 \sqrt{3}$ , 5. $12 \sqrt{3}$ , 6. $0$ .

Wstaw w tekst odpowiednie liczby.

$3 \sqrt{3}$ , $6 \sqrt{3}$ , $0$ , $12 \sqrt{3}$ , $12$ , $6$

Odległość prostej $D D'$ od płaszczyzny $A F F' A'$ wynosi .............
Odległość prostej $E E'$ od płaszczyzny $C D D' C'$ wynosi .............
Odległość prostej $F F'$ od płaszczyzny $A F F' A'$ wynosi .............
Odległość prostej $A' B'$ od płaszczyzny $A B C D E F$ wynosi .............

R13ziEsLxA3eq2

Ćwiczenie 5

Zaznacz zdanie, które jest prawdziwe.

Jeżeli prosta jest zawarta w płaszczyźnie, to nie jest równoległa do każdej prostej zawartej w tej płaszczyźnie.
Jeżeli prosta jest równoległa do płaszczyzny, to jest prostopadła do każdej prostej zawartej w tej płaszczyźnie.
Jeżeli prosta jest równoległa do płaszczyzny, to nie ma punktów wspólnych z tą płaszczyzną.

Ćwiczenie 6

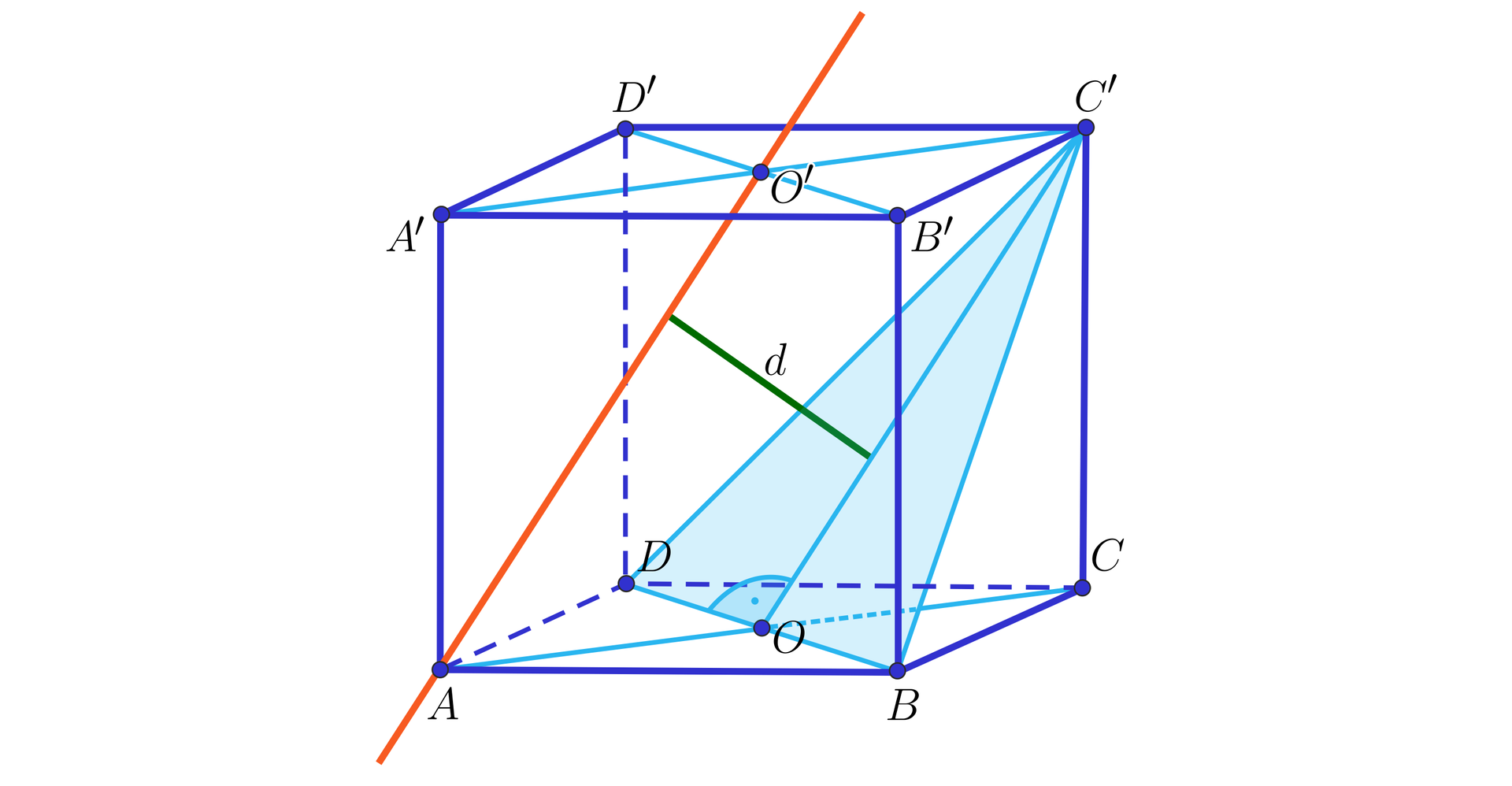
Na rysunku przedstawiono sześcian $A B C D A' B' C' D'$ o krawędzi długości $3 \sqrt{2}$ .

R15SgXMrFwglF

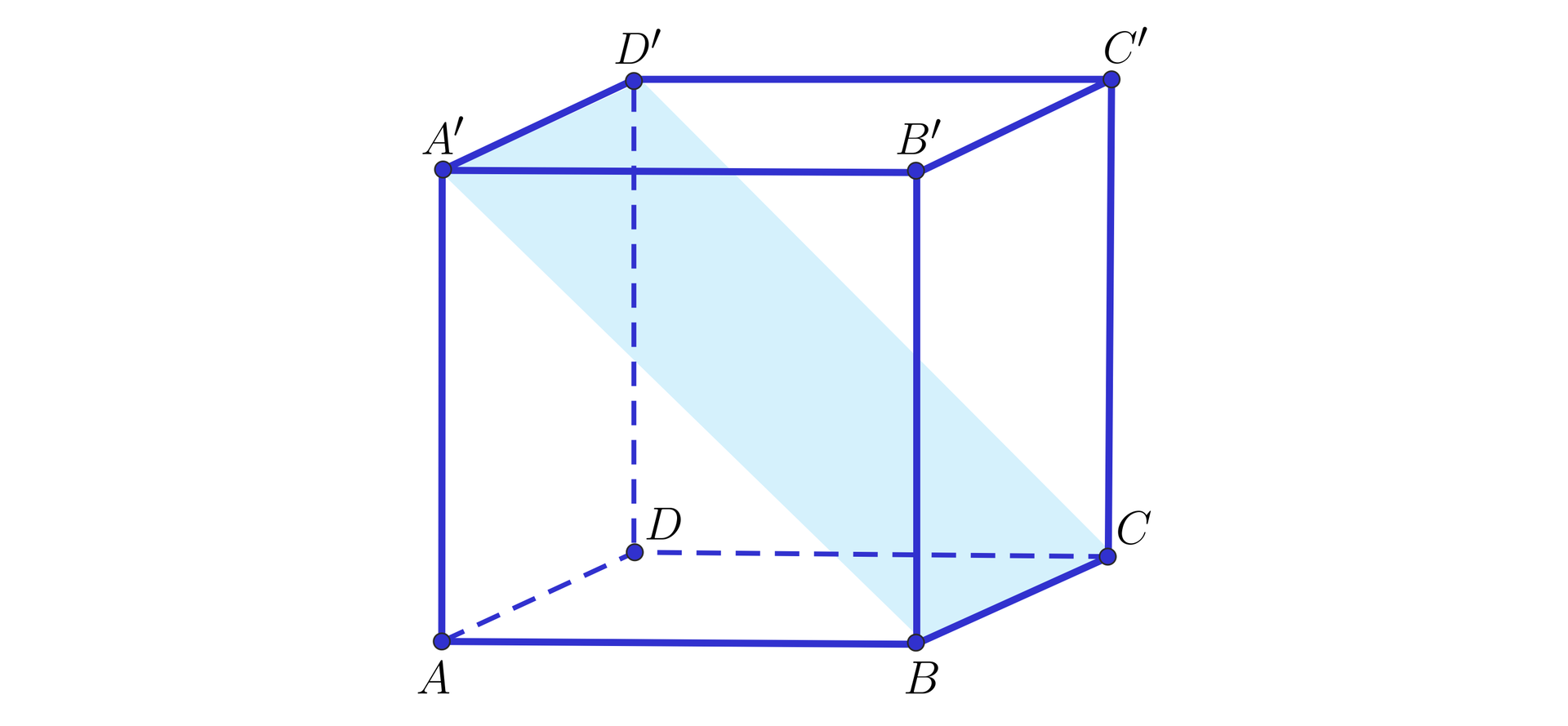
Grafika przedstawia sześcian, którego wierzchołki dolnej podstawy opisano A, B, C, D a wierzchołki górnej podstawy opisano: A', B', C', D', <mi. Wierzchołki B, C, A' oraz D' tworzą płaszczyznę, której krawędzie to przekątne ścian bocznych oraz krawędzie dolnej i górnej podstawy.

R1dfxe1qMRBah

Uzupełnij tekst odpowiednimi liczbami.

Odległość prostej $B' C'$ od płaszczyzny $B C D' A'$ wynosi .............
Odległość prostej $A' B$ od płaszczyzny $B C D' A'$ wynosi .............
Istnieją ............ proste, które zawierają krawędzie prostopadłościanu takie, że ich odległość od płaszczyzny $B C D' A'$ wynosi $3$ .

Ćwiczenie 7

Dany jest sześcian $A B C D A' B' C' D'$ , którego krawędź ma długość $a$ . Wykaż, że odległość $d$ prostej $A O'$ , gdzie $O'$ jest punktem przecięcia przekątnych podstawy $A' B' C' D'$ , od płaszczyzny $D B C'$ wynosi $d = \frac{a \sqrt{3}}{3}$ .

Narysujmy sześcian i wprowadźmy oznaczenia, jak na rysunku.

RDBVLhKtYoKC5

Grafika przedstawia sześcian, którego wierzchołki dolnej podstawy opisano A, B, C, D a wierzchołki górnej podstawy opisano: A', B', C', D', <mi. W obu podstawach zostały narysowane ich przekątne, punkt przecięcia się przekątnych w dolnej podstawie podpisano O, a w górnej podstawie O'. Punkty B, D oraz C' tworzą trójkąt, a punkty O ,A'stanowią wysokość trójkąta. Przez punkty A oraz O' przechodzi prosta. Wewnątrz sześcianu narysowano linię d, która łączy prostą przechodzącą przez punkty A i O' oraz wysokość trójkąta B, D C'.

Zauważmy, że czworokąt $A O C' O'$ jest równoległobokiem.

Wiadomo, że $a$ jest długością krawędzi sześcianu.

Zatem ${|A O'|}^{2} = a^{2} + {(\frac{a \sqrt{2}}{2})}^{2}$ .

Wobec tego $|A O'| = \sqrt{\frac{3}{2} a^{2}} = \frac{a \sqrt{6}}{2}$ .

Pole równoległoboku $A O C O'$ wynosi:

$P = a \cdot \frac{a \sqrt{2}}{2}$

oraz

$P = \frac{a \sqrt{6}}{2} \cdot d$ .

Zatem:

$a \cdot \frac{a \sqrt{2}}{2} = \frac{a \sqrt{6}}{2} \cdot d$ .

Wobec tego:

$d = \frac{a \sqrt{3}}{3}$ .

Ćwiczenie 8

Wyznacz dla jakich wartości parametru $m$ prosta $k$ określona przez wektor kierunkowy $\vec{u} = [m^{2}, 2, 3]$ jest równoległa do płaszczyzny $π$ określonej przez wektor normalny $\vec{v} = [m, - m^{2}, - 3]$ .

Do wyznaczenia wartości parametru $m$ sprawdzimy, kiedy zachodzi warunek $\vec{u} \circ \vec{v} = 0$ .

Wobec tego:

$\vec{u} \circ \vec{v} = [m^{2}, 2, 3] \circ [m, - m^{2}, - 3] = m^{3} - 2 m^{2} - 9$ .

Rozwiązujemy równanie $m^{3} - 2 m^{2} - 9 = 0$ .

Równanie przekształcamy do postaci

$(m^{2} + m + 3) \cdot (m - 3) = 0$

$m^{2} + m + 3 = 0 \lor m - 3 = 0$ .

Równanie $m^{2} + m + 3 = 0$ nie ma rozwiązania, zatem $m = 3$ .

Omawiana prosta jest równoległa do płaszczyzny, gdy $m = 3$ .

Animacja 3D

Dla nauczyciela