Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

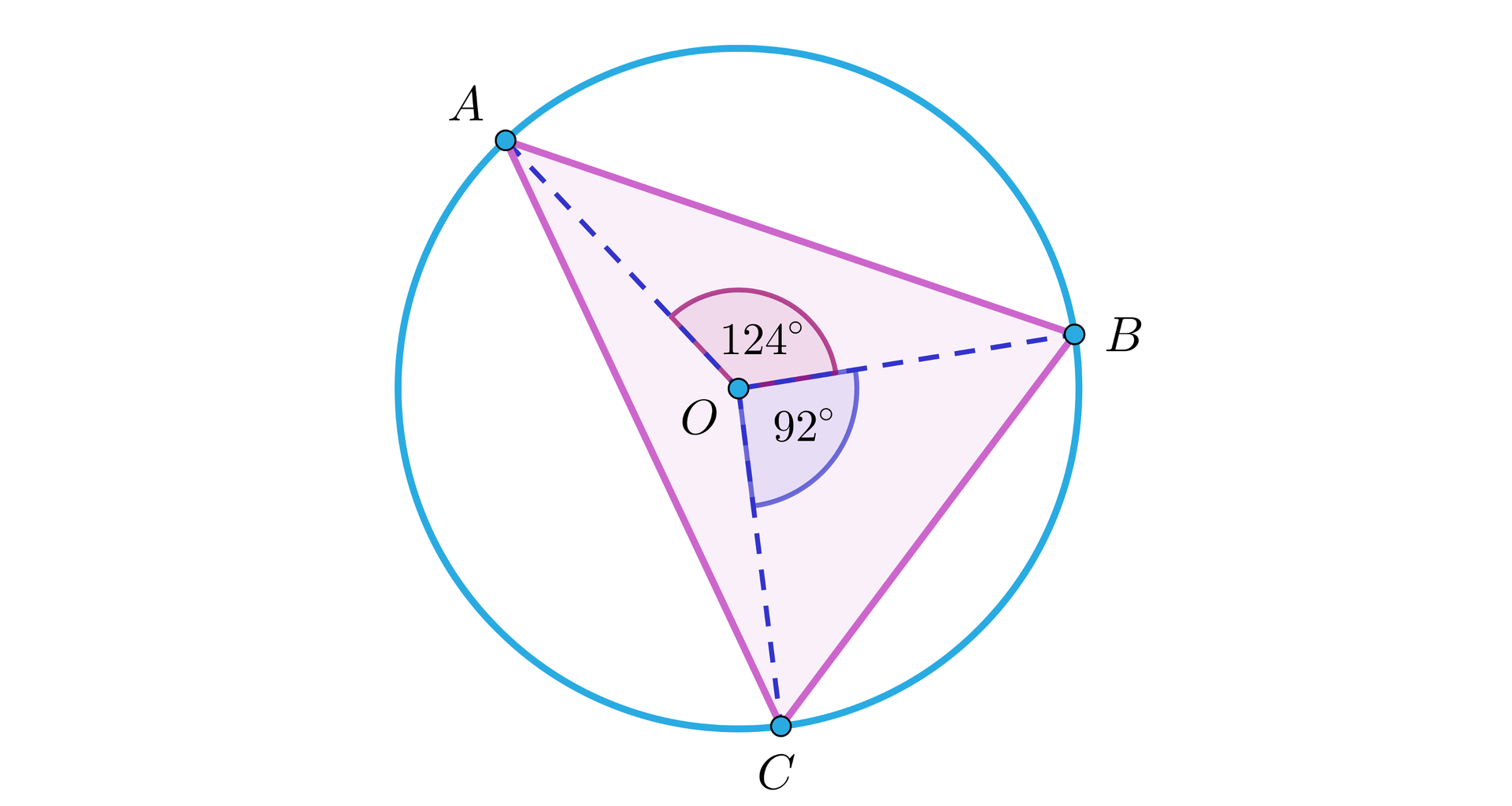
Na okręgu wyznaczono łuki $A B$ i $B C$ . Kąty środkowe oparte na tych łukach mają odpowiednio miary $124 °$ i $92 °$ . Wyznacz miary kątów trójkąta $A B C$ .

Popatrzmy na rysunek ilustrujący dane z zadania.

R13bfYhklMbUy

Grafika przedstawia okrąg, w który wpisany jest trójkąt. Środek okręgu jest podpisany literą O. Wierzchołki trójkąta, kolejno: A, B, C leżą na okręgu. Trójkąt ma kolor różowy. Odcinki AO, BO oraz CO są narysowane linią przerywaną. Kąt pomiędzy odcinkiem AO a odcinkiem BO ma wartość 124 stopnie. Kąt pomiędzy odcinkiem CO a BO ma wartość 92 stopnie.

Kąt $A C B$ jest kątem wpisanym oparty na tym samym łuku, co kąt środkowy $A O B$ , zatem $|∡ A C B| = \frac{1}{2} \cdot 124 ° = 62 °$ .

Analogicznie kąt $C A B$ jest kątem wpisanym oparty na tym samym łuku, co kąt środkowy $B O C$ , zatem $|∡ B A C| = \frac{1}{2} \cdot 92 ° = 46 °$ .

Z bilansu kątów trójkąta wynika, że $|∡ A B C| = 180 ° - 62 ° - 46 ° = 72 °$ .

Ćwiczenie 2

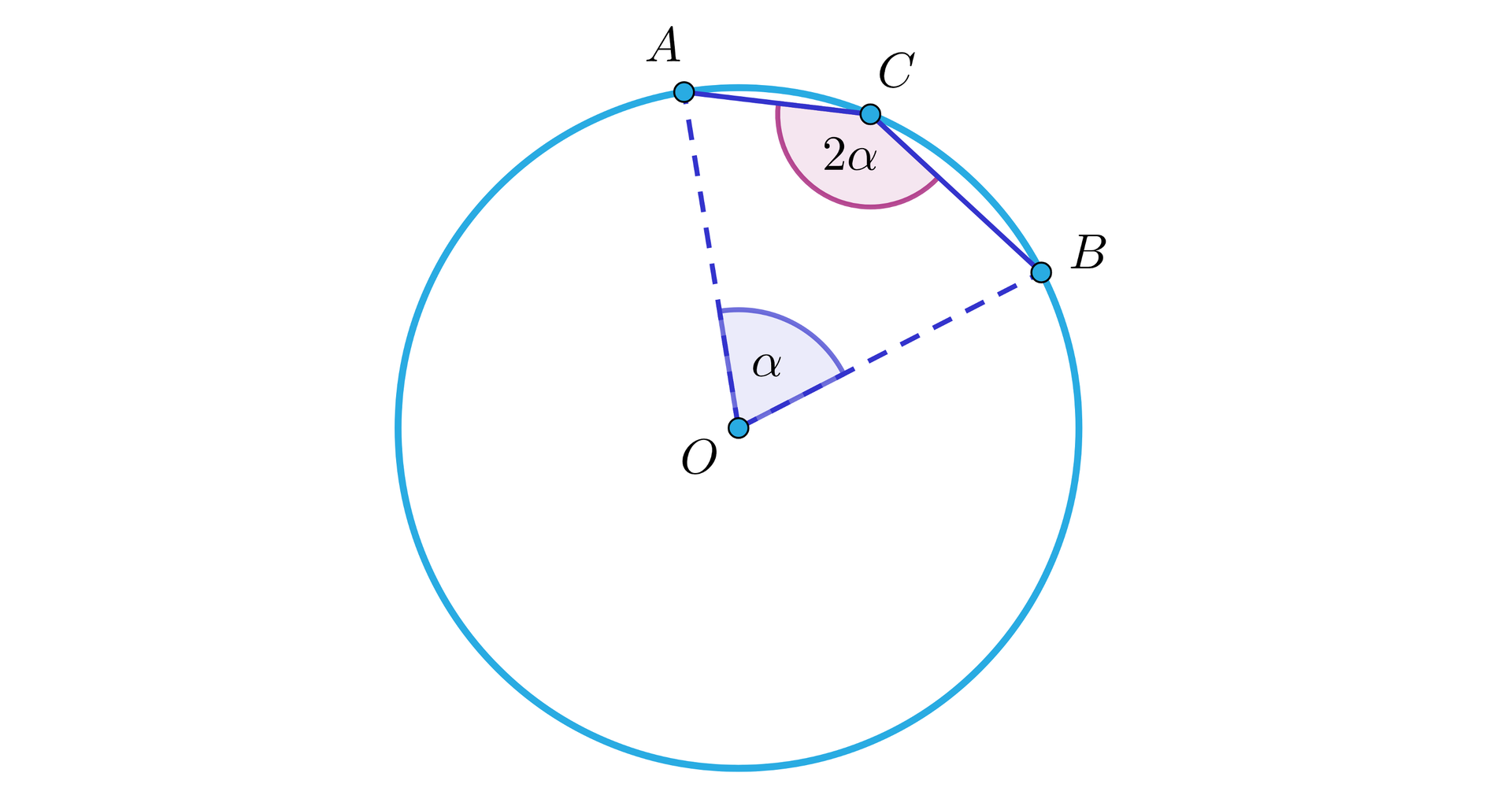
Dany jest okrąg o środku w punkcie $O$ i cięciwa $A B$ tego okręgu. Na okręgu wyznaczono taki punkt $C$ , że $2 \cdot |∡ A O B| = |∡ A C B|$ . Wyznacz miarę kąta $A O B$ .

Kąt $A O B$ jest kątem środkowym w danym okręgu, a kąt $A C B$ jest kątem wpisanym.

Oczywiście nie jest możliwe, aby były oparte na tym samy łuku.

Zatem kąt $A C B$ jest oparty na łuku, który jest dopełnieniem do całego okręgu tego łuku, na którym oparty jest kąt środkowy $A O B$ , jak na rysunku.

R1FyUYdA6BXRL

Grafika przedstawia okrąg. Środek okręgu jest podpisany literą O. Punkty: A, B, C leżą na okręgu, w taki sposób, ze punkt C znajduje się pomiędzy punktem A i punktem B. Odcinki AO i BO są narysowane linią przerywaną. Kąt pomiędzy odcinkiem AO a odcinkiem BO ma wartość jest podpisany literą alfa. Kąt pomiędzy odcinkiem

Oznaczmy przez $α$ miarę kąta $A O B$ . Wtedy mamy: $2 α = \frac{1}{2} \cdot (360 ° - α)$ .

Stąd $α = 72 °$ .

RkxPCMJa4Ylrd1

Ćwiczenie 3

R1StuSzKVBlGK2

Ćwiczenie 4

RgJB3xgsNs6ww

R1DhcdlffcqHZ2

Ćwiczenie 5

Ćwiczenie 6

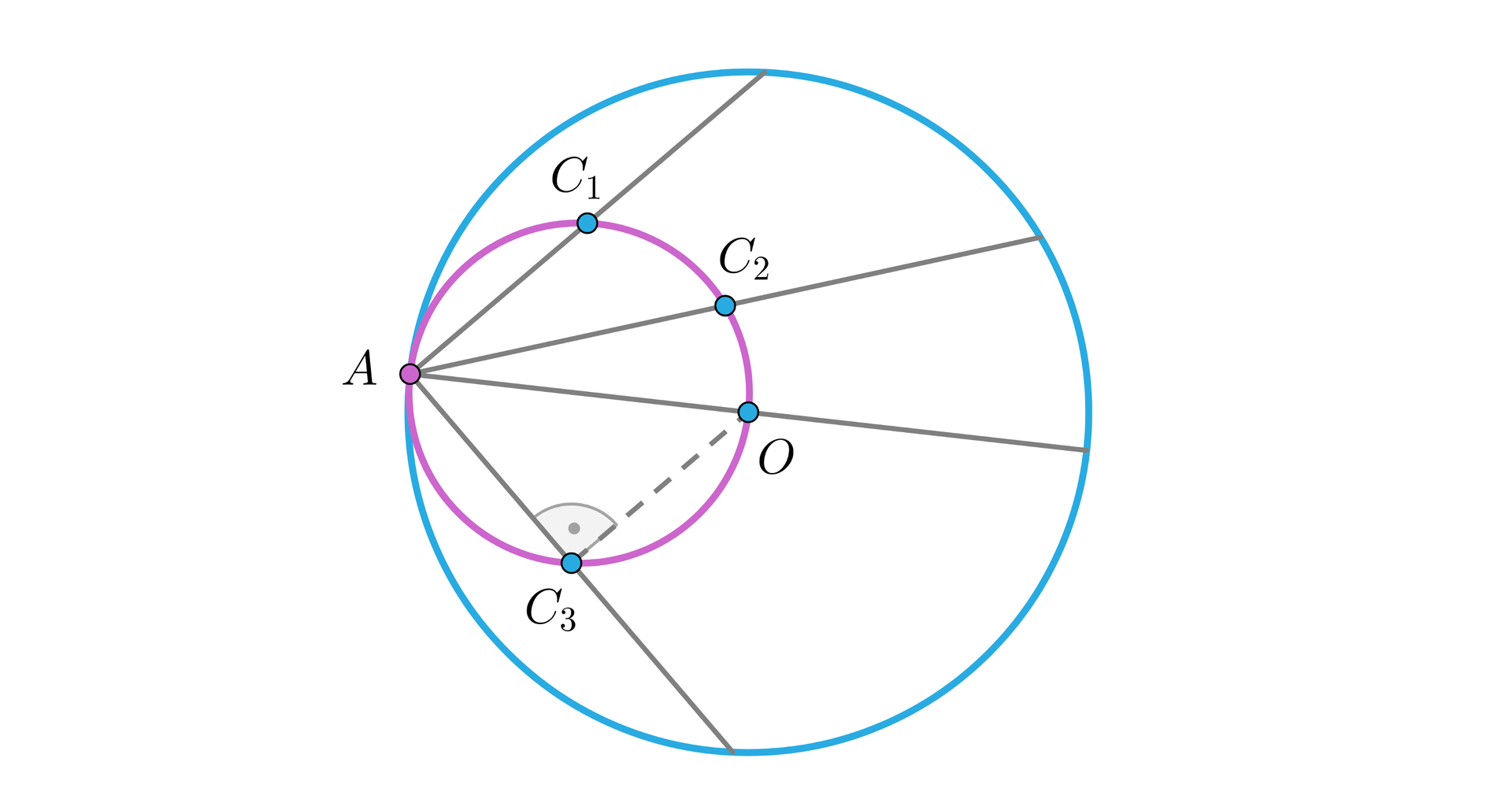
Wyznacz miejsce geometryczne punktów, które są środkami cięciw poprowadzonych z ustalonego punktu na danym okręgu.

Popatrzmy na rysunek.

R1DWJ8BHxTGWE

Grafika przedstawia dwa okręgi. Jeden okrąg znajduje się wewnątrz drugiego. Okręgi mają wspólny punkt podpisany litera A. Środek większego okręgu jest podpisany literą O. Mniejszy okrąg przechodzi przez punkt O. Na mniejszym okręgu, oprócz punktu O, znajdują się jeszcze , punkty: C dolny indeks 1, C dolny indeks 2 oraz C dolny indeks 3. Z punktu A przez wszystkie punkty znajdujące się na mniejszym okręgu zostały poprowadzone linie, które stanowią cięciwy większego okręgu. Pomiędzy punktem C dolny indeks 3 i Puntem O narysowany został odcinek. Odcinek ten jest pod kątem prostym do odcinka C dolny indeks 3, A.

Punkty $C_{1}$ , $C_{2}$ , $C_{3}$ są środkami różnych cięciw poprowadzonych z ustalonego punktu $A$ .

Oczywiście środek $O$ danego okręgu spełnia warunki zadania.

Zauważmy ponadto, że każdy promień okręgu przechodzący przez środek cięciwy jest do tej cięciwy prostopadły.

Zatem szukamy miejsca geometrycznego punktów, z których dany odcinek $A O$ jest widoczny pod kątem prostym.

Z twierdzenia Talesa dla kąta wpisanego wynika, że rozwiązaniem jest każdy z półokręgów (bez końców) wraz z punktem $O$ .

Ćwiczenie 7

Okrąg o średnicy $B C$ przecina bok $A B$ trójkąta $A B C$ w punkcie $D$ , jak na rysunku.

RnfYgoF3nVjOg

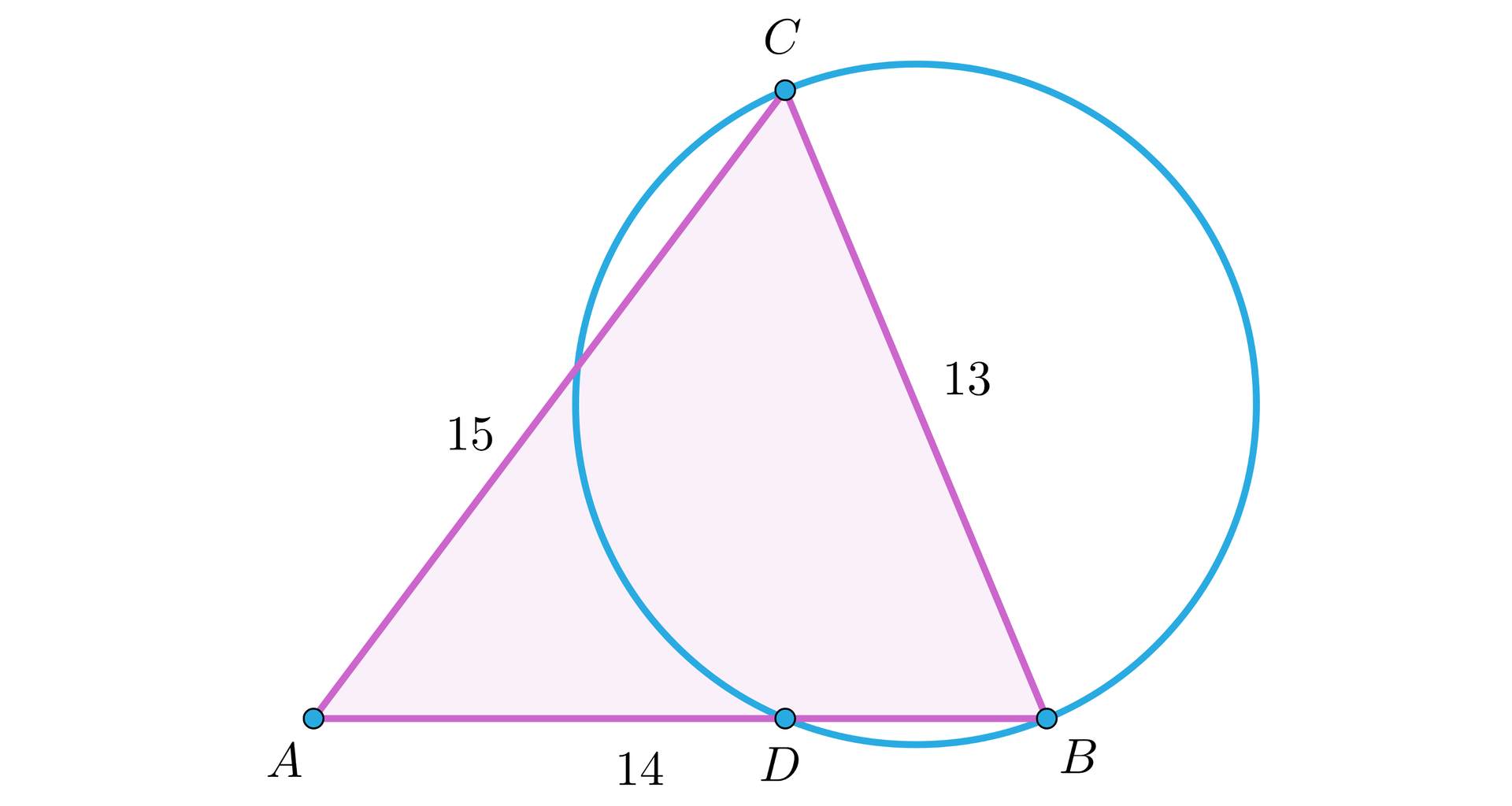
Grafika przedstawia okrąg oraz trójkąt. Na okręgu zaznaczone są 3 punkty: B, C, D. Poza okręgiem, z lewej strony znajduje się punkt A. Wierzchołki trójkąta to punkty A, B i C, przy czym Punkt D leży na odcinku AB. Długość odcinka AC to 15. Długość odcinka AB to 14, długość odcinka BC to 13.

Długości boków trójkąta są odpowiednio równe: $|A B| = 14$ , $|A C| = 15$ , $|B C| = 13$ . Oblicz długość odcinka $A D$ .

Oznaczmy długość odcinka $A D$ przez $x$ .

Kąt wpisany $B D C$ , jako rozpięty na średnicy okręgu jest kątem prostym, zatem trójkąty $B D C$ i $A D C$ są prostokątne.

Zatem: $x^{2} + {|C D|}^{2} = 15^{2}$ oraz ${(14 - x)}^{2} + {|C D|}^{2} = 13^{2}$ .

Odejmując stronami oba równania otrzymujemy: $x^{2} - {(14 - x)}^{2} = 15^{2} - 13^{2}$ , czyli $28 x - 196 = 225 - 169$ .

Stąd $x = 9$ .

Ćwiczenie 8

Na niewspółliniowych odcinkach $A B$ i $B C$ , jako na średnicach, wykreślono dwa okręgi. Okręgi te przecinają się w punkcie $D \neq B$ (patrz rysunek).

RVNB8sFZsc75x

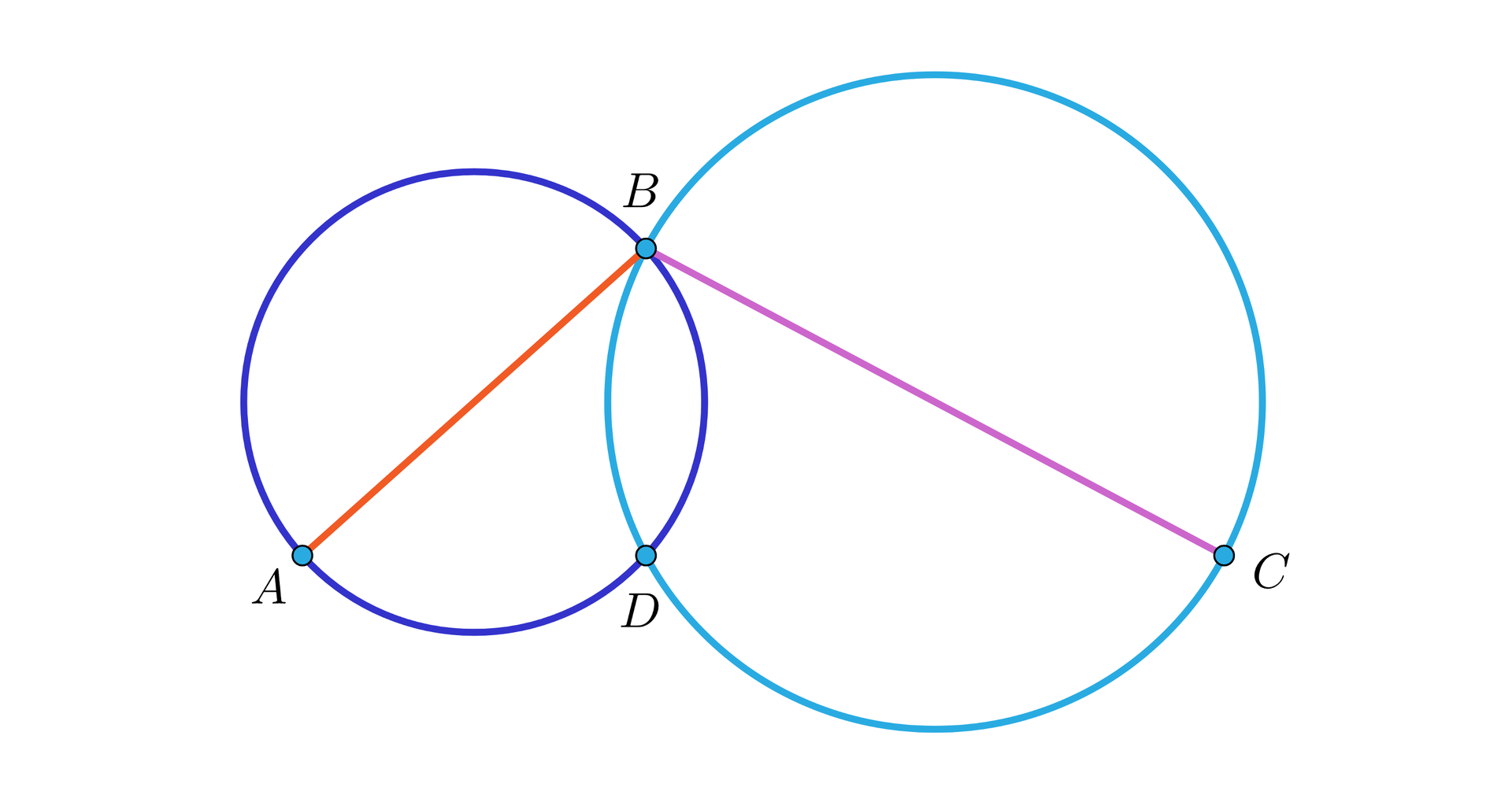
Grafika przedstawia dwa okręgi. Okręgi nachodzą na siebie. Miejsca przecięcia okręgów są zaznaczone punktami B i D. Na mniejszym okręgu znajduje się punkt A. Na większym okręgu znajduje się punkt C. W mniejszym okręgu został narysowany odcinek AB. W większym okręgu narysowany został odcinek BC.

R1SQfgKquMKPR

Udowodnij, że punkt

D

leży na prostej

A C

.
Ułóż w kolejności etapy dowodu.

Dowód: Elementy do uszeregowania: 1. Analogicznie, punkt

D

jest wierzchołkiem kąta wpisanego opartego na średnicy

B C

., 2. Miara kąta

A D C

jest zatem równa:

|∡ A D C| = |∡ A D B| + |∡ B D C| = 90 ° + 90 ° = 180 °

., 3. Ponownie skorzystamy z twierdzenia Talesa o kącie wpisanym, by stwierdzić, że tym razem kąt

B D C

jest kątem prostym., 4. Zauważmy, że kąt

A D C

jest sumą kątów

A D B

B D C

., 5. Punkt

D

jest wierzchołkiem kąta wpisanego opartego na średnicy

A B

., 6. Zatem punkty

A

D

C

są współliniowe, co należało wykazać., 7. Z twierdzenia Talesa o kącie wpisanym wynika, że kąt

A D B

jest kątem prostym.

Aplet

Dla nauczyciela