Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

RKeBneMHltuQI

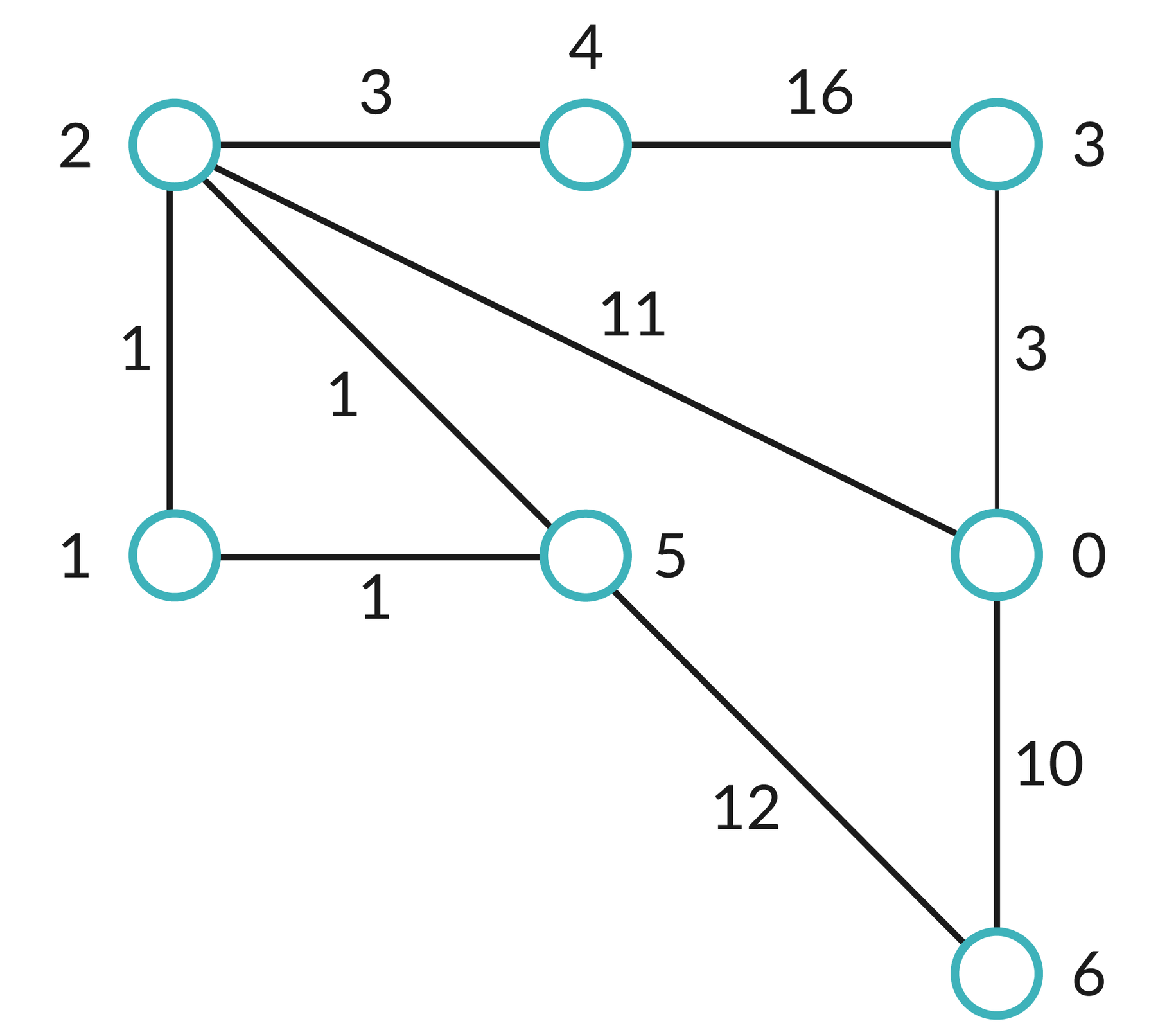
Graf jest przedstawiony z wartościami krawędzi i oznaczonymi wierzchołkami. Od wierzchołka trzy prowadzi krawędź o długości szesnaćsie do wierchołka cztery i krawędź o długości trzy do wierzchołkac zero. Od wierzchołka cztery poprowadzono ścieżkę o długości trzy do wierzchołka dwa. Od wierzchołka dwa poprowadzona jest ściezka o długości jedenascie do wierzchołka zero, o długości jeden do wierchołka pięć, o długości jeden do wierzchołka jeden. Od wierzchołka jeden krawędź od długości jeden do wierzchołka pięć. Od wierzchołka pięć do wierzchołka sześć krawędź ma długość dwanaście. Od wierzchołka sześć poprowadzona jest krawędź o długości dziesięć do wierzchołka zero. — Źródło: Contentplus.pl sp. z o.o., licencja: CC BY-SA 3.0.

RvylmYNysQGCN

Wskaż wyniki, które algorytm Dijkstry zwróci dla przedstawionego grafu. Za wierzchołek początkowy przyjmujemy wierzchołek 3. Zaznacz wszystkie poprawne odpowiedzi.

Tablice d[] zawierają długości ścieżek do kolejnych wierzchołków, a tablice p[] – poprzedniki tych wierzchołków.

Ćwiczenie 2

Napisz program, który dla grafu reprezentowanego przez macierz sąsiedztwa wypisze dwie tablice – najkrótszych ścieżek do danych wierzchołków oraz poprzedników tych wierzchołków.

Działanie programu przetestuj dla następujących danych:

int macierzSasiedztwa[V][V] = {
	{ 0, 5, 4, 2, 7 },
	{ 5, 0, 1, 0, 8 },
	{ 4, 1, 0, 22, 4 },
	{ 2, 0, 22, 0, 0 },
	{ 7, 8, 4, 0, 0 }
};

int s = 4;

Specyfikacja problemu:

Dane:

s – wierzchołek początkowy grafu
macierzSasiedztwa – tablica dwuwymiarowa; macierz sąsiedztwa grafu
V – liczba naturalna dodatnia; liczba wierzchołków grafu

Wynik:

tablica przechowująca najkrótsze ścieżki od wierzchołka s do pozostałych wierzchołków oraz tablica przechowująca poprzedniki kolejnych wierzchołków

Wynik dla podanych danych:

Wynik algorytmu Dijkstry:
d[V] = { 7 5 4 9 0 }
p[V] = { 4 2 4 0 -1 }

RsGn9gtsCejyG1

Linia 1. kratka include otwórz nawias ostrokątny iostream zamknij nawias ostrokątny. Linia 3. using namespace std średnik. Linia 5. const int V znak równości 5 średnik. Linia 6. const int nieskonczonosc znak równości 10000 średnik. Linia 8. int d otwórz nawias kwadratowy V zamknij nawias kwadratowy średnik. Linia 9. int p otwórz nawias kwadratowy V zamknij nawias kwadratowy średnik. Linia 10. bool S otwórz nawias kwadratowy V zamknij nawias kwadratowy średnik. Linia 12. void Dijkstra otwórz nawias okrągły int macierzSasiedztwa otwórz nawias kwadratowy V zamknij nawias kwadratowy otwórz nawias kwadratowy V zamknij nawias kwadratowy przecinek int s zamknij nawias okrągły otwórz nawias klamrowy. Linia 13. int u przecinek v średnik. Linia 14. int waga średnik. Linia 15. int odwiedzony znak równości 0 średnik. Linia 17. for otwórz nawias okrągły v znak równości 0 średnik v otwórz nawias ostrokątny V średnik v plus plus zamknij nawias okrągły otwórz nawias klamrowy. Linia 18. d otwórz nawias kwadratowy v zamknij nawias kwadratowy znak równości nieskonczonosc średnik. Linia 19. p otwórz nawias kwadratowy v zamknij nawias kwadratowy znak równości minus 1 średnik. Linia 20. S otwórz nawias kwadratowy v zamknij nawias kwadratowy znak równości false średnik. Linia 21. zamknij nawias klamrowy. Linia 23. d otwórz nawias kwadratowy s zamknij nawias kwadratowy znak równości 0 średnik. Linia 25. while otwórz nawias okrągły odwiedzony otwórz nawias ostrokątny V zamknij nawias okrągły otwórz nawias klamrowy. Linia 26. for otwórz nawias okrągły u znak równości 0 średnik S otwórz nawias kwadratowy u zamknij nawias kwadratowy znak równości znak równości true średnik u plus plus zamknij nawias okrągły średnik. Linia 27. for otwórz nawias okrągły v znak równości u plus 1 średnik v otwórz nawias ostrokątny V średnik v plus plus zamknij nawias okrągły. Linia 28. if otwórz nawias okrągły d otwórz nawias kwadratowy v zamknij nawias kwadratowy otwórz nawias ostrokątny d otwórz nawias kwadratowy u zamknij nawias kwadratowy ampersant ampersant S otwórz nawias kwadratowy v zamknij nawias kwadratowy znak równości znak równości false zamknij nawias okrągły u znak równości v średnik. Linia 30. S otwórz nawias kwadratowy u zamknij nawias kwadratowy znak równości true średnik. Linia 31. odwiedzony plus plus średnik. Linia 33. for otwórz nawias okrągły int i znak równości 0 średnik i otwórz nawias ostrokątny V średnik i plus plus zamknij nawias okrągły otwórz nawias klamrowy. Linia 34. if otwórz nawias okrągły macierzSasiedztwa otwórz nawias kwadratowy u zamknij nawias kwadratowy otwórz nawias kwadratowy i zamknij nawias kwadratowy zamknij nawias ostrokątny 0 zamknij nawias okrągły otwórz nawias klamrowy. Linia 35. v znak równości i średnik. Linia 36. waga znak równości macierzSasiedztwa otwórz nawias kwadratowy u zamknij nawias kwadratowy otwórz nawias kwadratowy i zamknij nawias kwadratowy średnik. Linia 38. if otwórz nawias okrągły d otwórz nawias kwadratowy v zamknij nawias kwadratowy zamknij nawias ostrokątny d otwórz nawias kwadratowy u zamknij nawias kwadratowy plus waga zamknij nawias okrągły otwórz nawias klamrowy. Linia 39. d otwórz nawias kwadratowy v zamknij nawias kwadratowy znak równości d otwórz nawias kwadratowy u zamknij nawias kwadratowy plus waga średnik. Linia 40. p otwórz nawias kwadratowy v zamknij nawias kwadratowy znak równości u średnik. Linia 41. zamknij nawias klamrowy. Linia 42. zamknij nawias klamrowy. Linia 43. zamknij nawias klamrowy. Linia 44. zamknij nawias klamrowy. Linia 45. zamknij nawias klamrowy. Linia 47. int main otwórz nawias okrągły zamknij nawias okrągły otwórz nawias klamrowy. Linia 48. int macierzSasiedztwa otwórz nawias kwadratowy V zamknij nawias kwadratowy otwórz nawias kwadratowy V zamknij nawias kwadratowy znak równości otwórz nawias klamrowy. Linia 49. otwórz nawias klamrowy 0 przecinek 5 przecinek 4 przecinek 2 przecinek 7 zamknij nawias klamrowy przecinek. Linia 50. otwórz nawias klamrowy 5 przecinek 0 przecinek 1 przecinek 0 przecinek 8 zamknij nawias klamrowy przecinek. Linia 51. otwórz nawias klamrowy 4 przecinek 1 przecinek 0 przecinek 22 przecinek 4 zamknij nawias klamrowy przecinek. Linia 52. otwórz nawias klamrowy 2 przecinek 0 przecinek 22 przecinek 0 przecinek 0 zamknij nawias klamrowy przecinek. Linia 53. otwórz nawias klamrowy 7 przecinek 8 przecinek 4 przecinek 0 przecinek 0 zamknij nawias klamrowy. Linia 54. zamknij nawias klamrowy średnik. Linia 56. Dijkstra otwórz nawias okrągły macierzSasiedztwa przecinek 4 zamknij nawias okrągły średnik. Linia 58. cout otwórz nawias ostrokątny otwórz nawias ostrokątny cudzysłów Wynik algorytmu Dijkstry dwukropek cudzysłów otwórz nawias ostrokątny otwórz nawias ostrokątny endl otwórz nawias ostrokątny otwórz nawias ostrokątny cudzysłów d otwórz nawias kwadratowy V zamknij nawias kwadratowy znak równości otwórz nawias klamrowy cudzysłów średnik. Linia 60. for otwórz nawias okrągły int i znak równości 0 średnik i otwórz nawias ostrokątny V średnik i plus plus zamknij nawias okrągły. Linia 61. cout otwórz nawias ostrokątny otwórz nawias ostrokątny d otwórz nawias kwadratowy i zamknij nawias kwadratowy otwórz nawias ostrokątny otwórz nawias ostrokątny cudzysłów cudzysłów średnik. Linia 63. cout otwórz nawias ostrokątny otwórz nawias ostrokątny cudzysłów zamknij nawias klamrowy cudzysłów otwórz nawias ostrokątny otwórz nawias ostrokątny endl otwórz nawias ostrokątny otwórz nawias ostrokątny cudzysłów p otwórz nawias kwadratowy V zamknij nawias kwadratowy znak równości otwórz nawias klamrowy cudzysłów średnik. Linia 65. for otwórz nawias okrągły int i znak równości 0 średnik i otwórz nawias ostrokątny V średnik i plus plus zamknij nawias okrągły. Linia 66. cout otwórz nawias ostrokątny otwórz nawias ostrokątny p otwórz nawias kwadratowy i zamknij nawias kwadratowy otwórz nawias ostrokątny otwórz nawias ostrokątny cudzysłów cudzysłów średnik. Linia 68. cout otwórz nawias ostrokątny otwórz nawias ostrokątny cudzysłów zamknij nawias klamrowy cudzysłów otwórz nawias ostrokątny otwórz nawias ostrokątny endl średnik. Linia 69. zamknij nawias klamrowy.

#include <iostream>

using namespace std;

const int V = 5;
const int nieskonczonosc = 10000;

int d[V];
int p[V];
bool S[V];

void Dijkstra(int macierzSasiedztwa[V][V], int s) {
	int u, v;
	int waga;
	int odwiedzony = 0;

	for (v = 0; v < V; v++) {
		d[v] = nieskonczonosc;
		p[v] = -1;
		S[v] = false;
	}

	d[s] = 0;

	while (odwiedzony < V) {
		for (u = 0; S[u] == true; u++);
		for (v = u + 1; v < V; v++)
			if (d[v] < d[u] && S[v] == false) u = v;

		S[u] = true;
		odwiedzony++;

		for (int i = 0; i < V; i++) {
			if (macierzSasiedztwa[u][i] > 0) {
				v = i;
				waga = macierzSasiedztwa[u][i];

				if (d[v] > d[u] + waga) {
					d[v] = d[u] + waga;
					p[v] = u;
				}
			}
		}
	}
}

int main() {
	int macierzSasiedztwa[V][V] = {
		{ 0, 5, 4, 2, 7 },
		{ 5, 0, 1, 0, 8 },
		{ 4, 1, 0, 22, 4 },
		{ 2, 0, 22, 0, 0 },
		{ 7, 8, 4, 0, 0 }
	};

	Dijkstra(macierzSasiedztwa, 4);

	cout << "Wynik algorytmu Dijkstry:" << endl << "d[V] = { ";

	for (int i = 0; i < V; i++)
		cout << d[i] << " ";

	cout << "}" << endl << "p[V] = { ";

	for (int i = 0; i < V; i++)
		cout << p[i] << " ";

	cout << "}" << endl;
}

Ćwiczenie 3

Napisz program, który dla danej tablicy poprzedników grafu wypisze kompletne ścieżki do kolejnych wierzchołków. Ścieżki powinny zaczynać się w wierzchołku początkowym, a kończyć na docelowym.

Działanie programu przetestuj dla następujących danych:

int p[V] = { 4, 2, 4, 0, -1 };

Specyfikacja problemu:

Dane:

p – tablica poprzedników; tablica liczb całkowitych
V – liczba naturalna dodatnia; liczba wierzchołków grafu

Wynik:

komunikat dotyczący najkrótszych ścieżek do kolejnych wierzchołków

Wynik dla podanych danych:

Ścieżka do 0: 4 0 
Ścieżka do 1: 4 2 1 
Ścieżka do 2: 4 2 
Ścieżka do 3: 4 0 3 
Ścieżka do 4: 4

Ri8uUT2ehMlHI

#include <iostream>

using namespace std;

const int V = 5;

int p[V] = { 4, 2, 4, 0, -1 };

void drukujSciezke(int v) {
    if (p[v] > -1) {
        drukujSciezke(p[v]);
    }
    cout << v << " ";
}

int main() {
    for (int v = 0; v < V; ++v) {
        cout << "Ścieżka do " << v << ": ";
        drukujSciezke(v);
        cout << endl;
    }
    return 0;
}

Ćwiczenie 4

Zmodyfikuj program tak, by algorytm Dijkstry działał dla grafu, którego każda krawędź ma wagę równą 1.

Działanie programu przetestuj dla następujących danych:

int listaSasiedztwa[V][maksymalnieSasiadow] = {
    {3, 4, 1, 2, 5, -1},
    {0, 2, 4, 5, 3, -1},
    {3, -1, -1, -1, -1, -1},
    {5, -1, -1, -1, -1, -1},
    {1, 2, -1, -1, -1, -1},
    {1, 2, -1, -1, -1, -1}
};

int s = 4;

Specyfikacja problemu:

Dane:

listaSasiedztwa – tablica dwuwymiarowa; lista sąsiedztwa grafu
s – wierzchołek początkowy grafu
V – liczba naturalna dodatnia; liczba wierzchołków grafu

Wynik:

tablica przechowująca najkrótsze ścieżki od wierzchołka s do pozostałych wierzchołków oraz tablica przechowująca poprzedniki kolejnych wierzchołków

Wynik dla podanych danych:

Wynik algorytmu Dijkstry:
d[V] = { 2 1 1 2 0 2 }
p[V] = { 1 4 4 1 -1 1 }

R1u03vGb192D21

Linia 1. kratka include otwórz nawias ostrokątny iostream zamknij nawias ostrokątny. Linia 3. using namespace std średnik. Linia 5. const int V znak równości 6 średnik. Linia 6. const int maksymalnieSasiadow znak równości 6 średnik. Linia 7. const int nieskonczonosc znak równości 10000 średnik. Linia 9. int d otwórz nawias kwadratowy V zamknij nawias kwadratowy średnik. Linia 10. int p otwórz nawias kwadratowy V zamknij nawias kwadratowy średnik. Linia 11. bool S otwórz nawias kwadratowy V zamknij nawias kwadratowy średnik. Linia 13. int listaSasiedztwa otwórz nawias kwadratowy V zamknij nawias kwadratowy otwórz nawias kwadratowy maksymalnieSasiadow zamknij nawias kwadratowy znak równości otwórz nawias klamrowy. Linia 14. otwórz nawias klamrowy 3 przecinek 4 przecinek 1 przecinek 2 przecinek 5 przecinek minus 1 zamknij nawias klamrowy przecinek. Linia 15. otwórz nawias klamrowy 0 przecinek 2 przecinek 4 przecinek 5 przecinek 3 przecinek minus 1 zamknij nawias klamrowy przecinek. Linia 16. otwórz nawias klamrowy 3 przecinek minus 1 przecinek minus 1 przecinek minus 1 przecinek minus 1 przecinek minus 1 zamknij nawias klamrowy przecinek. Linia 17. otwórz nawias klamrowy 5 przecinek minus 1 przecinek minus 1 przecinek minus 1 przecinek minus 1 przecinek minus 1 zamknij nawias klamrowy przecinek. Linia 18. otwórz nawias klamrowy 1 przecinek 2 przecinek minus 1 przecinek minus 1 przecinek minus 1 przecinek minus 1 zamknij nawias klamrowy przecinek. Linia 19. otwórz nawias klamrowy 1 przecinek 2 przecinek minus 1 przecinek minus 1 przecinek minus 1 przecinek minus 1 zamknij nawias klamrowy. Linia 20. zamknij nawias klamrowy średnik. Linia 22. void Dijkstra otwórz nawias okrągły int s zamknij nawias okrągły otwórz nawias klamrowy. Linia 23. int u przecinek v średnik. Linia 24. int odwiedzony znak równości 0 średnik. Linia 26. for otwórz nawias okrągły v znak równości 0 średnik v otwórz nawias ostrokątny V średnik v plus plus zamknij nawias okrągły otwórz nawias klamrowy. Linia 27. d otwórz nawias kwadratowy v zamknij nawias kwadratowy znak równości nieskonczonosc średnik. Linia 28. p otwórz nawias kwadratowy v zamknij nawias kwadratowy znak równości minus 1 średnik. Linia 29. S otwórz nawias kwadratowy v zamknij nawias kwadratowy znak równości false średnik. Linia 30. zamknij nawias klamrowy. Linia 31. d otwórz nawias kwadratowy s zamknij nawias kwadratowy znak równości 0 średnik. Linia 33. while otwórz nawias okrągły odwiedzony otwórz nawias ostrokątny V zamknij nawias okrągły otwórz nawias klamrowy. Linia 34. u znak równości minus 1 średnik. Linia 35. for otwórz nawias okrągły v znak równości 0 średnik v otwórz nawias ostrokątny V średnik v plus plus zamknij nawias okrągły. Linia 36. if otwórz nawias okrągły wykrzyknik S otwórz nawias kwadratowy v zamknij nawias kwadratowy ampersant ampersant otwórz nawias okrągły u znak równości znak równości minus 1 kreska pionowa kreska pionowa d otwórz nawias kwadratowy v zamknij nawias kwadratowy otwórz nawias ostrokątny d otwórz nawias kwadratowy u zamknij nawias kwadratowy zamknij nawias okrągły zamknij nawias okrągły u znak równości v średnik. Linia 38. if otwórz nawias okrągły d otwórz nawias kwadratowy u zamknij nawias kwadratowy znak równości znak równości nieskonczonosc zamknij nawias okrągły break średnik. Linia 40. S otwórz nawias kwadratowy u zamknij nawias kwadratowy znak równości true średnik. Linia 41. odwiedzony plus plus średnik. Linia 43. for otwórz nawias okrągły int i znak równości 0 średnik listaSasiedztwa otwórz nawias kwadratowy u zamknij nawias kwadratowy otwórz nawias kwadratowy i zamknij nawias kwadratowy wykrzyknik znak równości minus 1 średnik i plus plus zamknij nawias okrągły otwórz nawias klamrowy. Linia 44. v znak równości listaSasiedztwa otwórz nawias kwadratowy u zamknij nawias kwadratowy otwórz nawias kwadratowy i zamknij nawias kwadratowy średnik. Linia 45. if otwórz nawias okrągły d otwórz nawias kwadratowy v zamknij nawias kwadratowy zamknij nawias ostrokątny d otwórz nawias kwadratowy u zamknij nawias kwadratowy plus 1 zamknij nawias okrągły otwórz nawias klamrowy. Linia 46. d otwórz nawias kwadratowy v zamknij nawias kwadratowy znak równości d otwórz nawias kwadratowy u zamknij nawias kwadratowy plus 1 średnik. Linia 47. p otwórz nawias kwadratowy v zamknij nawias kwadratowy znak równości u średnik. Linia 48. zamknij nawias klamrowy. Linia 49. zamknij nawias klamrowy. Linia 50. zamknij nawias klamrowy. Linia 51. zamknij nawias klamrowy. Linia 53. int main otwórz nawias okrągły zamknij nawias okrągły otwórz nawias klamrowy. Linia 54. Dijkstra otwórz nawias okrągły 4 zamknij nawias okrągły średnik. Linia 56. cout otwórz nawias ostrokątny otwórz nawias ostrokątny cudzysłów Wynik algorytmu Dijkstry dwukropek cudzysłów otwórz nawias ostrokątny otwórz nawias ostrokątny endl otwórz nawias ostrokątny otwórz nawias ostrokątny cudzysłów d otwórz nawias kwadratowy V zamknij nawias kwadratowy znak równości otwórz nawias klamrowy cudzysłów średnik. Linia 57. for otwórz nawias okrągły int i znak równości 0 średnik i otwórz nawias ostrokątny V średnik i plus plus zamknij nawias okrągły. Linia 58. cout otwórz nawias ostrokątny otwórz nawias ostrokątny d otwórz nawias kwadratowy i zamknij nawias kwadratowy otwórz nawias ostrokątny otwórz nawias ostrokątny cudzysłów cudzysłów średnik. Linia 59. cout otwórz nawias ostrokątny otwórz nawias ostrokątny cudzysłów zamknij nawias klamrowy cudzysłów otwórz nawias ostrokątny otwórz nawias ostrokątny endl otwórz nawias ostrokątny otwórz nawias ostrokątny cudzysłów p otwórz nawias kwadratowy V zamknij nawias kwadratowy znak równości otwórz nawias klamrowy cudzysłów średnik. Linia 60. for otwórz nawias okrągły int i znak równości 0 średnik i otwórz nawias ostrokątny V średnik i plus plus zamknij nawias okrągły. Linia 61. cout otwórz nawias ostrokątny otwórz nawias ostrokątny p otwórz nawias kwadratowy i zamknij nawias kwadratowy otwórz nawias ostrokątny otwórz nawias ostrokątny cudzysłów cudzysłów średnik. Linia 62. cout otwórz nawias ostrokątny otwórz nawias ostrokątny cudzysłów zamknij nawias klamrowy cudzysłów otwórz nawias ostrokątny otwórz nawias ostrokątny endl średnik. Linia 64. return 0 średnik. Linia 65. zamknij nawias klamrowy.

#include <iostream>

using namespace std;

const int V = 6; 
const int maksymalnieSasiadow = 6; 
const int nieskonczonosc = 10000;

int d[V];
int p[V]; 
bool S[V]; 

int listaSasiedztwa[V][maksymalnieSasiadow] = {
    {3, 4, 1, 2, 5, -1},
    {0, 2, 4, 5, 3, -1},
    {3, -1, -1, -1, -1, -1},
    {5, -1, -1, -1, -1, -1},
    {1, 2, -1, -1, -1, -1},
    {1, 2, -1, -1, -1, -1}
};

void Dijkstra(int s) {
    int u, v;
    int odwiedzony = 0;

    for (v = 0; v < V; v++) {
        d[v] = nieskonczonosc;
        p[v] = -1;
        S[v] = false;
    }
    d[s] = 0; 

    while (odwiedzony < V) {
        u = -1;
        for (v = 0; v < V; v++)
            if (!S[v] && (u == -1 || d[v] < d[u])) u = v;

        if (d[u] == nieskonczonosc) break;

        S[u] = true;
        odwiedzony++;

        for (int i = 0; listaSasiedztwa[u][i] != -1; i++) {
            v = listaSasiedztwa[u][i];
            if (d[v] > d[u] + 1) {
                d[v] = d[u] + 1;
                p[v] = u;
            }
        }
    }
}

int main() {
    Dijkstra(4);

    cout << "Wynik algorytmu Dijkstry:" << endl << "d[V] = { ";
    for (int i = 0; i < V; i++)
        cout << d[i] << " ";
    cout << "}" << endl << "p[V] = { ";
    for (int i = 0; i < V; i++)
        cout << p[i] << " ";
    cout << "}" << endl;

    return 0;
}

RUjU2tvnUNdd931

Ćwiczenie 5

Jakich wyników algorytm Dijkstry na pewno nie zwróci? Możliwe odpowiedzi: 1. d[] = [7, 5, 4, 6, 0]
prev[] = [4, 2, 4, 2, -1], 2. d[] = [10, 5, 4, 6, 0]
prev[] = [4, 2, 4, 2, 2], 3. d[] = [10, 5, 4, 6, 0, 11, 12]
prev[] = [4, 2, 4, 2, -1, 4, 5], 4. d[] = [10, 5, 4, 6, -1, 11, 12, 1]
prev[] = [4, 2, 4, 2, -1, 4, 5, 0]

R1UyOLwJ2yDDD31

Ćwiczenie 6

Źródło: Contentplus.pl Sp. z o.o., licencja: CC BY-SA 3.0.

Ćwiczenie 6

RJFFlS9H7w7VB

Prezentacja multimedialna

Dla nauczyciela