Sprawdź się
Pokaż ćwiczenia:
Ćwiczenie 1
Ćwiczenie 2
Przedstawione na rysunku poniżej trójkąty równoramienne i są podobne. Co z tego wynika?

Ćwiczenie 3
Ćwiczenie 4
Ćwiczenie 5
Roczny procentowy przyrost przychodów pewnego przedsiębiorstwa w kolejnych czterech latach wynosił: , , , . Oblicz średni przyrost dochodów w tym okresie. Skorzystaj ze średniej geometrycznej (wynik zaokrąglij do ), odpowiedź podaj w procentach.
Ćwiczenie 6
Jeżeli liczby , , , są liczbami dodatnimi, to
. Elementy do uszeregowania: 1. Korzystamy z nierówności między średnią arytmetyczną, a geometryczną dla liczb i ., 2. Obie strony każdej z nierówności są dodatnie, zatem możemy pomnożyć stronami te nierówności., 3. Przekształcamy zapisaną nierówność dla liczb i ., 4. , 5. Przekształcamy zapisaną nierówność dla liczb i ., 6.
, 7. W wyniku przekształceń równoważnych, otrzymaliśmy dowodzoną nierówność, co kończy dowód., 8. , 9. , 10. Zapisujemy uzyskane nierówności jedna pod drugą., 11. , 12. , 13. Korzystamy z nierówności między średnią arytmetyczną, a geometryczną dla liczb i .
Ćwiczenie 7
Uzupełnij rozwiązanie zadania, przeciągnij odpowiednie wyrażenia. Oznaczmy przez , długości boków luka do uzupełnienia .
Na podstawie warunków zadania i twierdzenia Pitagorasa, zapisujemy:
luka do uzupełnienia
Pole prostokąta jest równe:
luka do uzupełnienia
Z zależności między średnią geometryczną a arytmetyczną wynika, że
luka do uzupełnienia
Przy czym równość zachodzi wtedy i tylko wtedy, gdy luka do uzupełnienia , czyli gdy .
Zatem:
luka do uzupełnienia
luka do uzupełnienia
Odpowiedź:
Największe pole ma kwadrat o boku długości .
Ćwiczenie 8
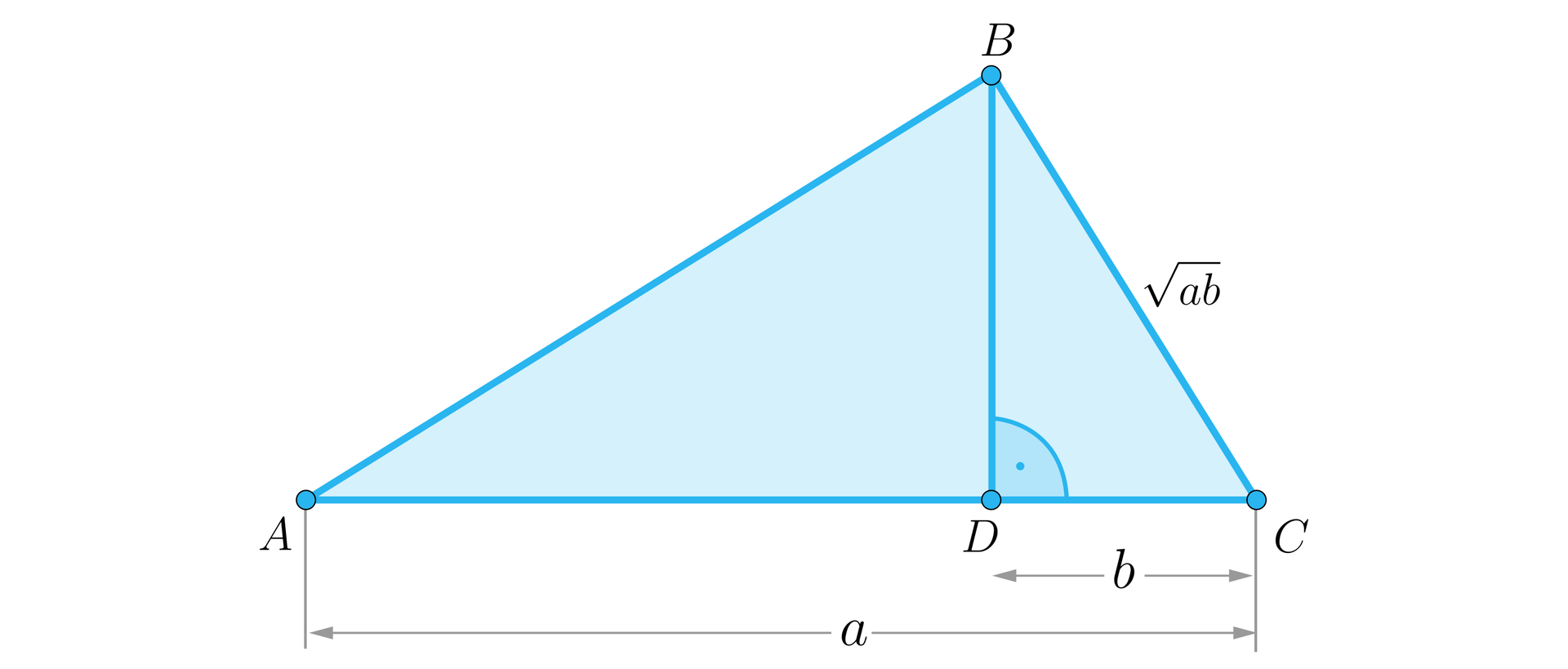
Trójkąt jest trójkątem prostokątnym, w którym przeciwprostokątna ma długość . Odcinek jest wysokością tego trójkąta i . Wykaż, że .