Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

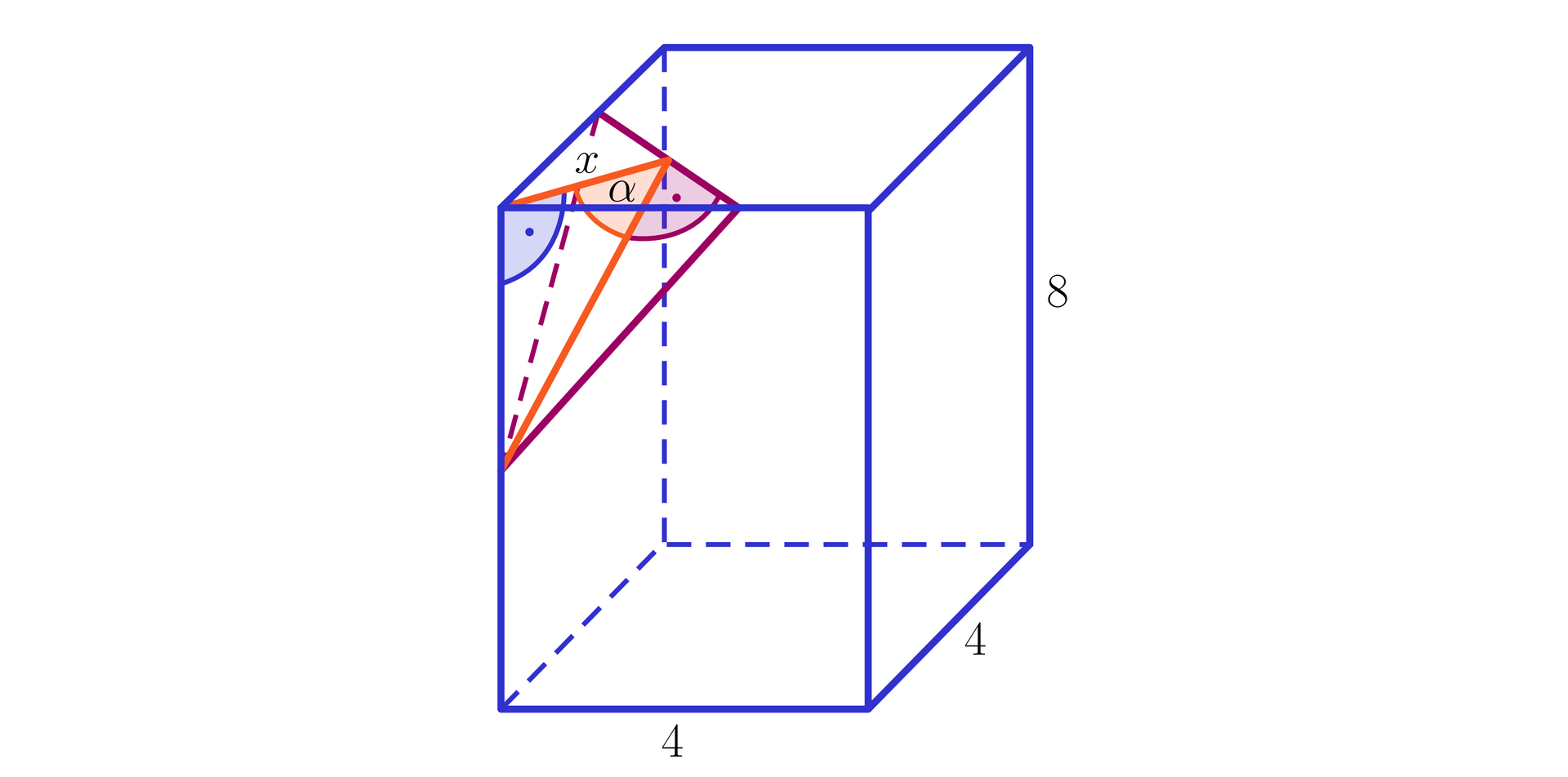
Wiadomo, że pole podstawy graniastosłupa prawidłowego czworokątnego z rysunku jest równe $49$ , a suma długości wszystkich krawędzi graniastosłupa jest równa $92$ . Wtedy miara kąta $α$ wynosi około:

R1Wzc7RJWOJsU

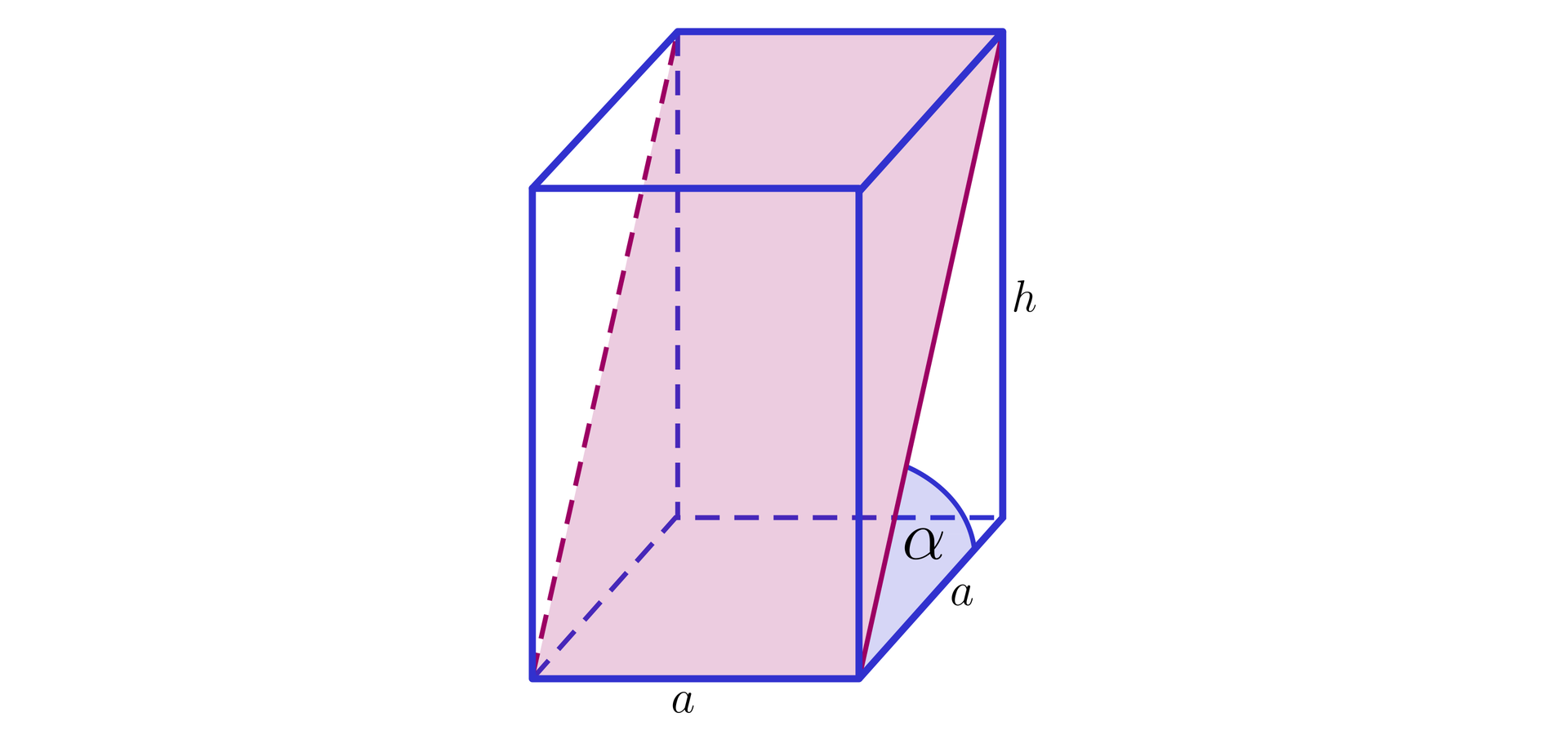
Na ilustracji przedstawiono graniastosłup prosty o podstawie kwadratu. Długości krawędzi podstawy oznaczono literą a, natomiast długość krawędzi bocznej oznaczono literą h. Zaznaczono przekrój graniastosłupa, którego płaszczyzna jest prostokątem. Boki prostokąta stanowią krawędzie podstaw graniastosłupa, oraz przekątne przeciwległych ścian bocznych graniastosłupa. Płaszczyzna przekroju jest nachylona do płaszczyzny podstawy pod kątem alfa.

R1PiqB9BIVZw5

Ćwiczenie 2

Wiadomo, że krawędź podstawy graniastosłupa prawidłowego czworokątnego z rysunku ma długość $8$ , a krawędź boczna ma długość $12$ . Zaznacz zdania, które są prawdziwe.

RVgLzmvGdcPws

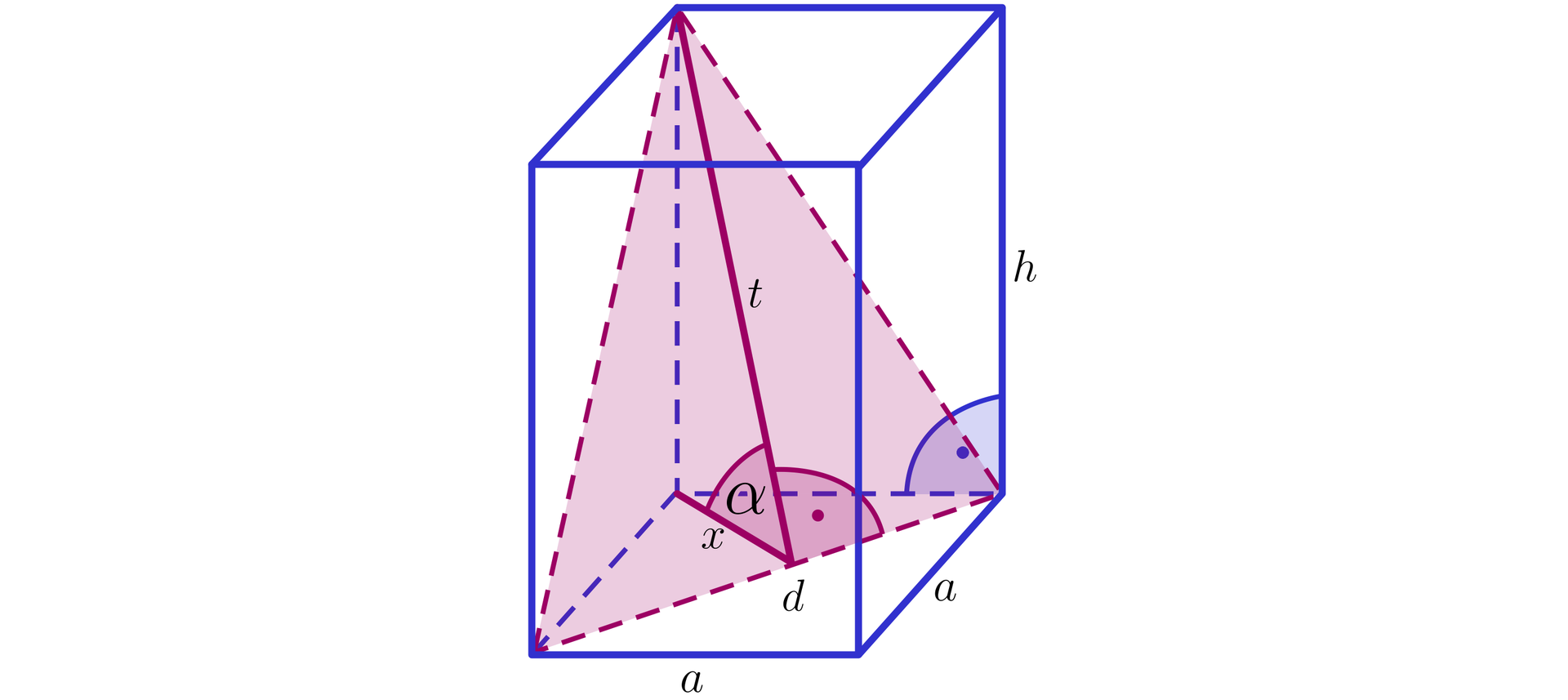
Ilustracja przedstawia graniastosłup prosty. Podstawę graniastosłupa stanowi kwadrat o długości krawędzi oznaczonej literą a, natomiast długość krawędzi bocznej oznaczono literą h. Zaznaczono przekrój graniastosłupa, którego płaszczyznę stanowi trójkąt ograniczony dwoma przekątnymi ścian bocznych wychodzącymi z jednego wierzchołka oraz przekątną podstawy. Zaznaczono wysokość trójkąta oznaczoną literą t, której spodek znajduje się na przekątnej d podstawy. Kąt nachylenia płaszczyzny przekroju do płaszczyzny podstawy oznaczono alfa. Odległość spodka wysokości trójkąta od wierzchołka dolnej podstawy, równoległego do wierzchołka skąd opuszczona jest wysokość trójkąta, wynosi x.

R8N4JuQMemKMf

Ćwiczenie 3

Na rysunku przedstawiono dwa przekroje graniastosłupa prawidłowego czworokątnego.

R1DT3jmQjNaMu

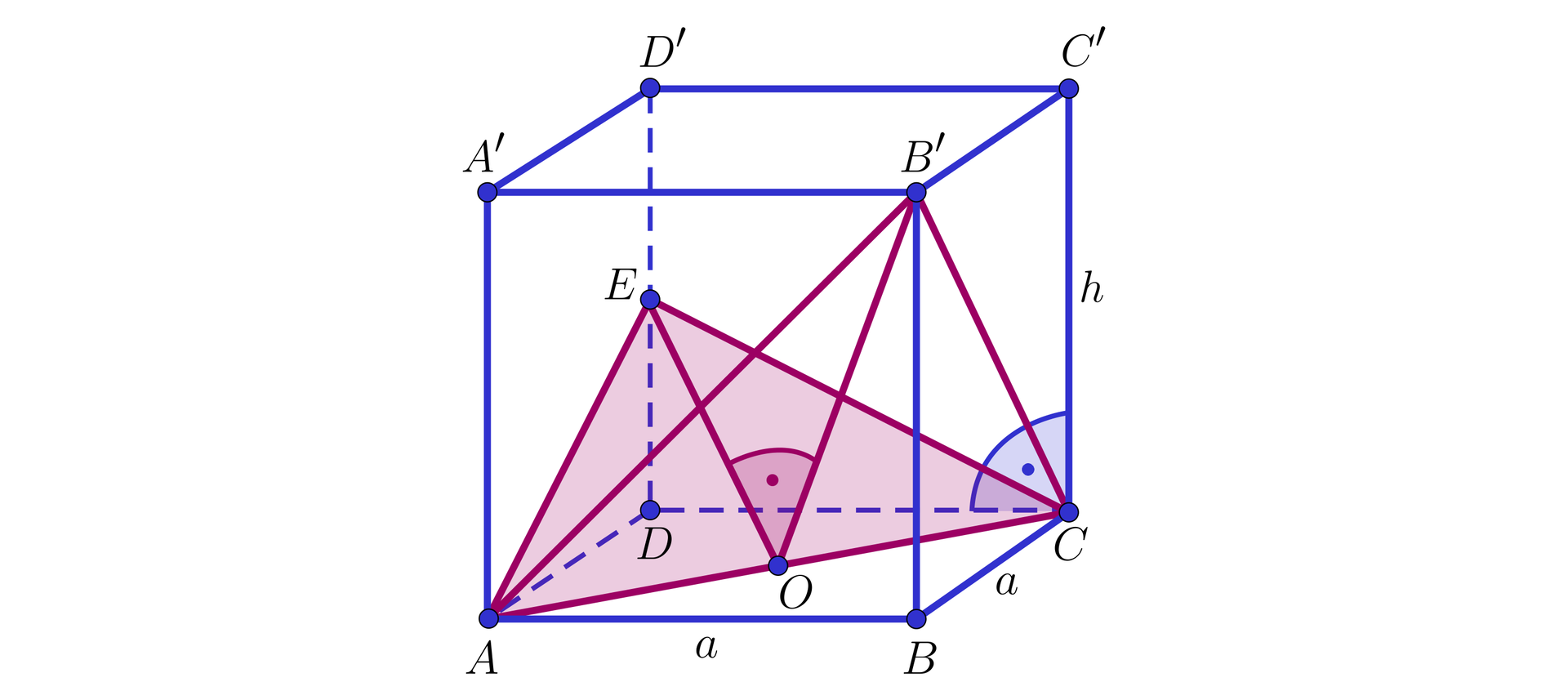
Na ilustracji przedstawiono graniastosłup prosty o podstawie kwadratu. Dolną podstawę oznaczono ABCD, natomiast górną A'B'C'D'. Odpowiednio nad wierzchołkiem A znajduje się wierzchołek A prim, nad wierzchołkiem B wierzchołek B prim i tak dalej. Długość krawędzi podstawy oznaczono literą a, natomiast długość krawędzi bocznej oznaczono literą h. Na krawędzi DD' zaznaczono punkt E stanowiący jej środek. Punkt O stanowi miejsce przecięcia przekątnych podstawy. Zaznaczono trójkąty ACE oraz AB'C, które stanowią płaszczyzny przekroju graniastosłupa. Kąt B'OE jest kątem prostym.

Punkt $E$ jest środkiem krawędzi $D D'$ , a punkt $O$ – punktem przecięcia przekątnych $A C$ i $B D$ podstawy graniastosłupa.

R3SGWpJYZSFP4

Ćwiczenie 4

R1PDDqCAgamvW

R1MoG0csRq3Qo

Ćwiczenie 5

Na rysunku przedstawiono przekrój graniastosłupa pewną płaszczyzną przechodzącą przez przekątną podstawy i środek krawędzi bocznej.

RDAVpYRjKxeCF

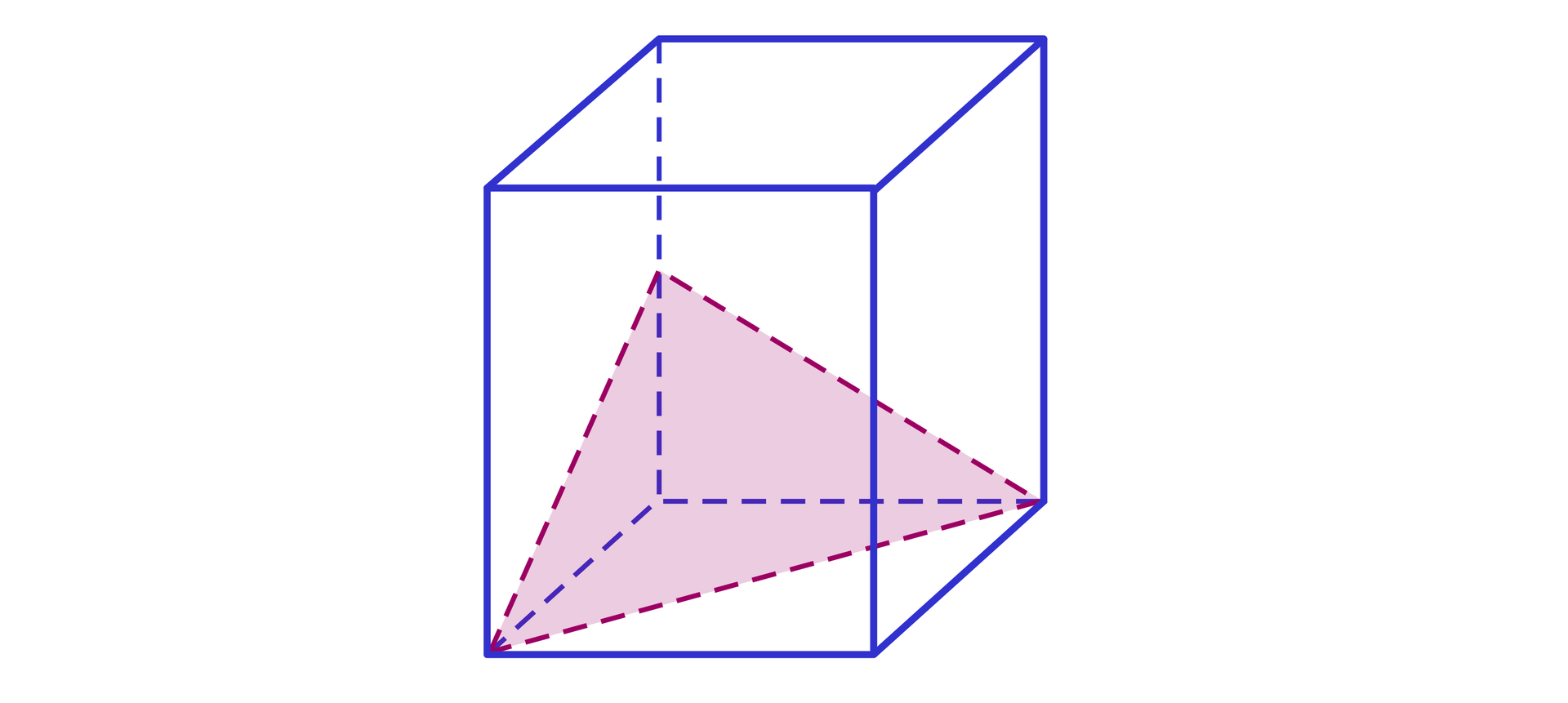
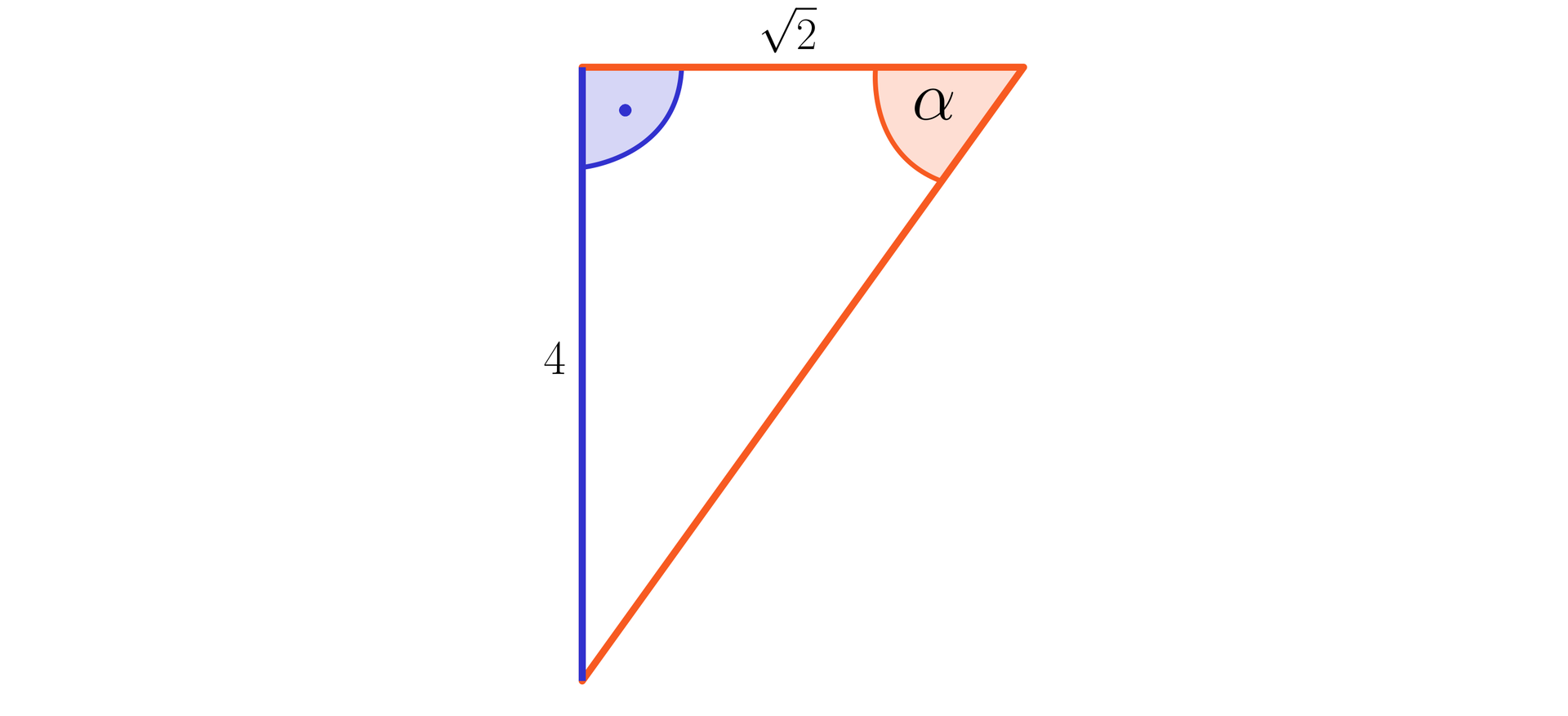
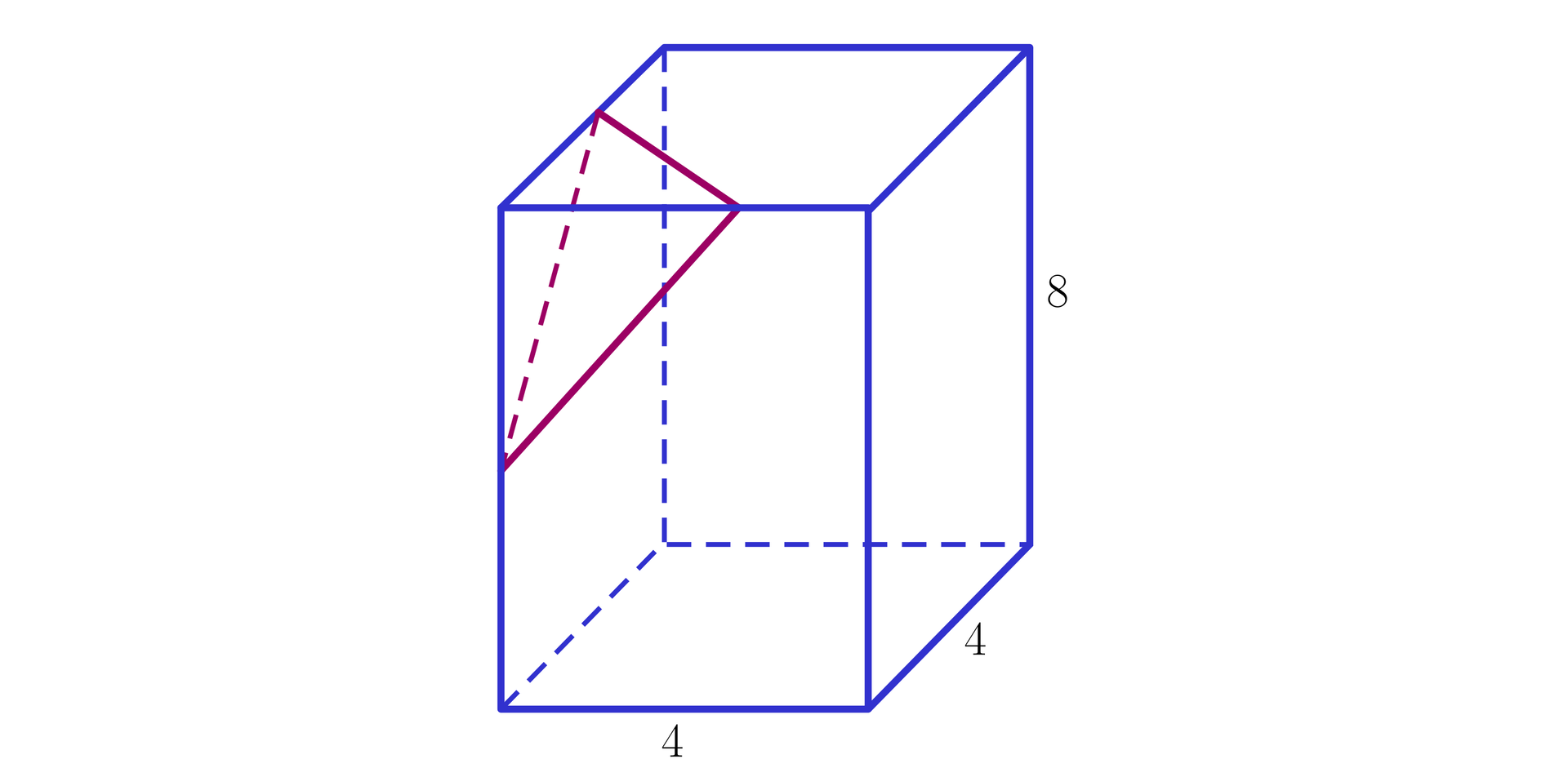
Na ilustracji przedstawiono graniastosłup o podstawie kwadratu. Zaznaczono w nim przekrój, którego płaszczyznę stanowi trójkąt. Jedna z krawędzi trójkąta zawiera się w przekątnej podstawy graniastosłupa. Pozostałe dwie krawędzie zawierają się w sąsiadujących ścianach bocznych. Wierzchołek z którego wychodzą dwie krawędzie trójkąta znajduję się w połowie krawędzi bocznej graniastosłupa.

R1lbAHLMbRRJR

Pogrupuj elementy, zgodnie z podanym opisem. Własności graniastosłupa prawidłowego czworokątnego o krawędzi podstawy długości

8

i wysokości

6

: Możliwe odpowiedzi: 1. element 1 grupy 1, 2. element 3 grupy 1, 3. element 2 grupy 2, 4. element 2 grupy 1, 5. element 1 grupy 2, 6. element 3 grupy 2 Własności graniastosłupa prawidłowego czworokątnego o krawędzi podstawy długości

6

i wysokości

8

: Możliwe odpowiedzi: 1. element 1 grupy 1, 2. element 3 grupy 1, 3. element 2 grupy 2, 4. element 2 grupy 1, 5. element 1 grupy 2, 6. element 3 grupy 2

Ćwiczenie 6

Graniastosłup prawidłowy czworokątny o krawędzi podstawy długości $4$ i wysokości $8$ przecięto płaszczyzną przechodzącą przez środki krawędzi wychodzących z jednego wierzchołka tak, jak na poniższym rysunku. Wyznacz miarę kąta nachylenia tej płaszczyzny do płaszczyzny górnej podstawy graniastosłupa.

RgqPaEHmZnvku

Na ilustracji przedstawiono graniastosłup prosty o podstawie kwadratu równej 4 i krawędzi bocznej równej osiem. Na graniastosłupie w lewym górnym rogu zaznaczono trójkąt. Jego wierzchołki przechodzą przez środki krawędzi wychodzących z jednego wierzchołka graniastosłupa.

Wprowadźmy dodatkowe oznaczenia i zaznaczmy odpowiedni kąt, jak na poniższym rysunku.

RoJpKhmOR8mj6

Zauważmy, że $x = \frac{1}{2} \cdot \frac{4 \sqrt{2}}{2} = \sqrt{2}$ .

Do wyznaczenia miary kąta $α$ rozpatrujemy trójkąt prostokątny, jak na poniższym rysunku.

REfst0YINviED

Na ilustracji przedstawiono trójkąt prostokątny o przyprostokątnych długości cztery i pierwiastek drugiego stopnia z dwóch. Naprzeciw przyprostokątnej długości cztery, zaznaczono kąt alfa.

Zatem $tg α = \frac{4}{\sqrt{2}} = 2 \sqrt{2}$ .

Korzystając z tablic wartości funkcji trygonometrycznych, odczytujemy że $α \approx 71 °$ .

Ćwiczenie 7

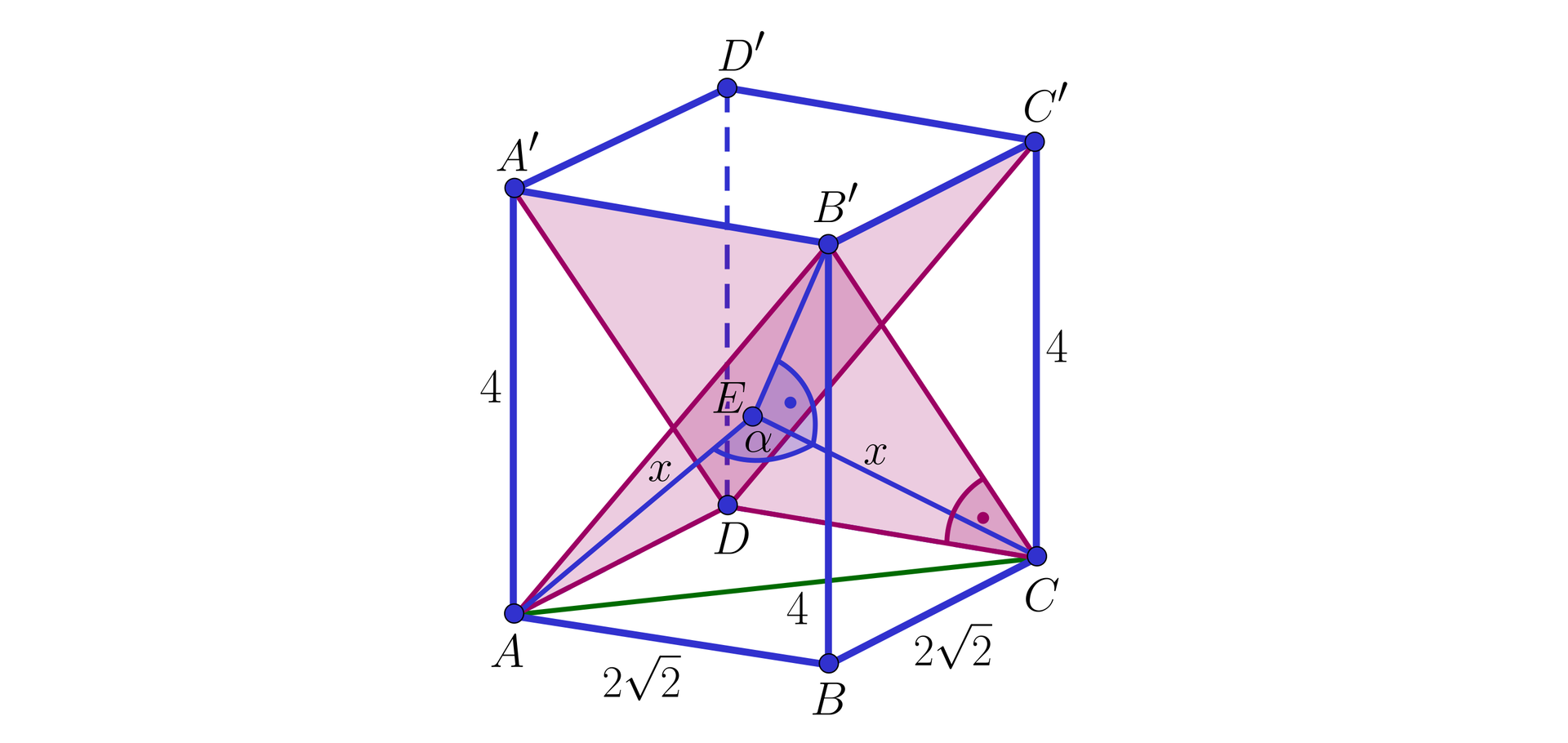
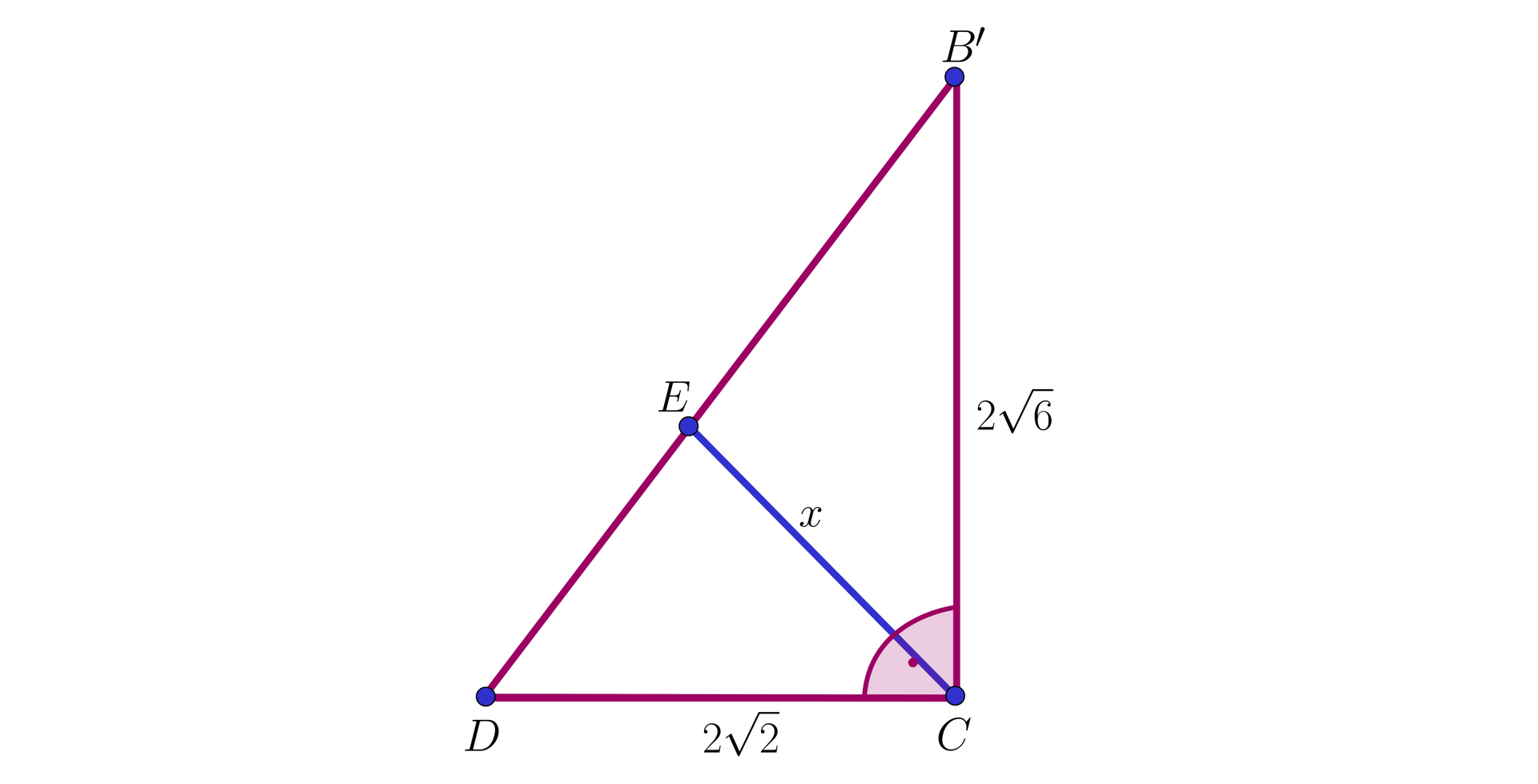
Graniastosłup prawidłowy czworokątny o krawędzi podstawy długości $2 \sqrt{2}$ i wysokości $4$ przecięto płaszczyznami, uzyskując przekroje $A D C' B'$ oraz $D C B' A'$ w kształcie prostokątów. Oblicz miarę kąta wyznaczonego przez płaszczyzny tych przekrojów.

RmgpfBjpg0y56

Wprowadźmy dodatkowe oznaczenia na rysunku i zaznaczmy odpowiedni kąt.

R1J3Oz6HTle9U

Na ilustracji przedstawiono graniastosłup prawidłowy czworokątny o długości krawędzi podstawy równej 22. Dolną podstawę oznaczono ABCD, natomiast górną A'B'C'D'. Odpowiednio nad wierzchołkiem A znajduje się wierzchołek A prim, nad wierzchołkiem B wierzchołek B prim i tak dalej. Zaznaczono prostokąty ADC'B' oraz DCB'A, które stanowią płaszczyzny przekroju graniastosłupa. Wysokość graniastosłupa wynosi cztery. Zaznaczono przekątną dolnej podstawy A C o długości cztery. Na przekątnej D B prim zaznaczono punkt E i połączono go z wierzchołkiem A i C, tak że powstał trójkąt równoramienny rozwartokątny A C E o ramionach długości x, podstawie cztery i kącie przy wierzchołku E miary alfa. Powstał też również trójkąt prostokątny E C B prim o kącie prostym przy wierzchołku E.

Korzystając z twierdzenia Pitagorasa mamy:

$|C B'| = \sqrt{{(2 \sqrt{2})}^{2} + 4^{2}} = \sqrt{8 + 16} = 2 \sqrt{6}$

$|D B'| = \sqrt{{(2 \sqrt{2})}^{2} + {(2 \sqrt{6})}^{2}} = \sqrt{8 + 24} = 4 \sqrt{2}$

RMuJYTd6AYqQ5

Na ilustracji przedstawiono trójkąt prostokątny ACB', z kątem prostym przy wierzchołku C. Przyprostokątne mają długości 22 i 26. Z wierzchołka C opuszczono wysokość długości x do przeciwprostokątnej DB', której spodek leży w punkcie E.

Korzystając z pola trójkąta, długość $x$ obliczamy, rozwiązując równanie:

$\frac{2 \sqrt{2} \cdot 2 \sqrt{6}}{2} = \frac{x \cdot 4 \sqrt{2}}{2}$

$x = \sqrt{6}$

Do wyznaczenia miary kąta $α$ korzystamy z trójkąta $A C E$ i twierdzenia cosinusów:

$4^{2} = x^{2} + x^{2} - 2 x \cdot x \cdot \cos α$

$16 = 6 + 6 - 2 \cdot 6 \cdot \cos α$

$\cos α = - \frac{1}{3}$

Wobec tego $α \approx 109 °$ .

Ćwiczenie 8

Graniastosłup prawidłowy czworokątny o krawędzi podstawy $8$ przecięto płaszczyzną przechodzącą przez środki dwóch sąsiednich krawędzi podstawy. Płaszczyzna ta przecina trzy krawędzie boczne i jest nachylona do płaszczyzny podstawy pod kątem $45 °$ . Oblicz pole tego przekroju.

Narysujmy graniastosłup prawidłowy czworokątny, jego przekrój oraz zaznaczmy omawiany kąt. Przekrojem graniastosłupa prawidłowego czworokątnego z zadania jest pięciokąt.

R1X9rOPvxO0Ir

Na ilustracji przedstawiono graniastosłup o podstawie dolnej ABCD, oraz górnej EFGH. Odpowiednio nad wierzchołkiem A znajduje się wierzchołek E, nad wierzchołkiem B wierzchołek F i tak dalej. Przekątne podstawy AC i BD przecinają się w punkcie S. Zaznaczono dwa punkty stanowiące środki krawędzi. Na krawędzi AB punkt M oraz na krawędzi BC punkt N. Zaznaczono płaszczyznę przekroju w kształcie pięciokąta, której wierzchołki stanowią punkty M, N, punkt O na krawędzi AE, punkt G na krawędzi CG, oraz punkt E na krawędzi DH. Linią przerywaną połączono punkty O i G. Z wierzchołka E poprowadzono prostą, przecinającą odcinek OG w punkcie K, oraz przekątną SB w punkcie L. ∠KSD jest kątem prostym, natomiast ∠SLK mierzy 45 stopni.

Otrzymany przekrój, będący pięciokątem możemy podzielić na trapez równoramienny i trójkąt równoramienny.

Korzystając z oznaczeń z rysunku mamy:

$\frac{|S L|}{|K L|} = \cos 45 °$

$|K L| = \frac{|S L|}{\frac{\sqrt{2}}{2}} = \sqrt{2} \cdot |S L| = \sqrt{2} \cdot \frac{1}{4} \cdot |B D| = \sqrt{2} \cdot \frac{1}{4} \cdot 8 \sqrt{2} = 4$

Zauważmy, że trójkąty $E D L$ i $K S L$ są podobne na mocy cechy podobieństwa trójkątów kkk, zatem $\frac{|E L|}{|K L|} = 3$ i $|E L| = 12$ , więc $|E K| = 12 - 4 = 8$ .

Zauważmy, że podstawy trapezu mają długości $8 \sqrt{2}$ i $4 \sqrt{2}$ .

Wobec tego pole trapezu jest równe:

$P = \frac{8 \sqrt{2} + 4 \sqrt{2}}{2} \cdot 4 = 24 \sqrt{2}$

Pole trójkąta jest równe:

$P = \frac{8 \sqrt{2} \cdot 8}{2} = 32 \sqrt{2}$

Wobec tego pole pięciokąta, będącego przekrojem omawianaego graniastosłupa prawidłowego czworokątnego jest równe:

$P = 24 \sqrt{2} + 32 \sqrt{2} = 56 \sqrt{2}$

Animacja 3D

Dla nauczyciela