Sprawdź się

Pokaż ćwiczenia:

R1B24x3YlfQdP1

Ćwiczenie 1

W graniastosłupie prawidłowym pięciokątnym suma długości krawędzi wynosi $20 cm$ . Wiedząc, że pole powierzchni bocznej jest największe z możliwych wyznacz długość krawędzi podstawy oraz wysokość.

$a =$ ............ $cm$

$H =$ ............ $cm$

Ćwiczenie 2

RCCnkY81pJo7p

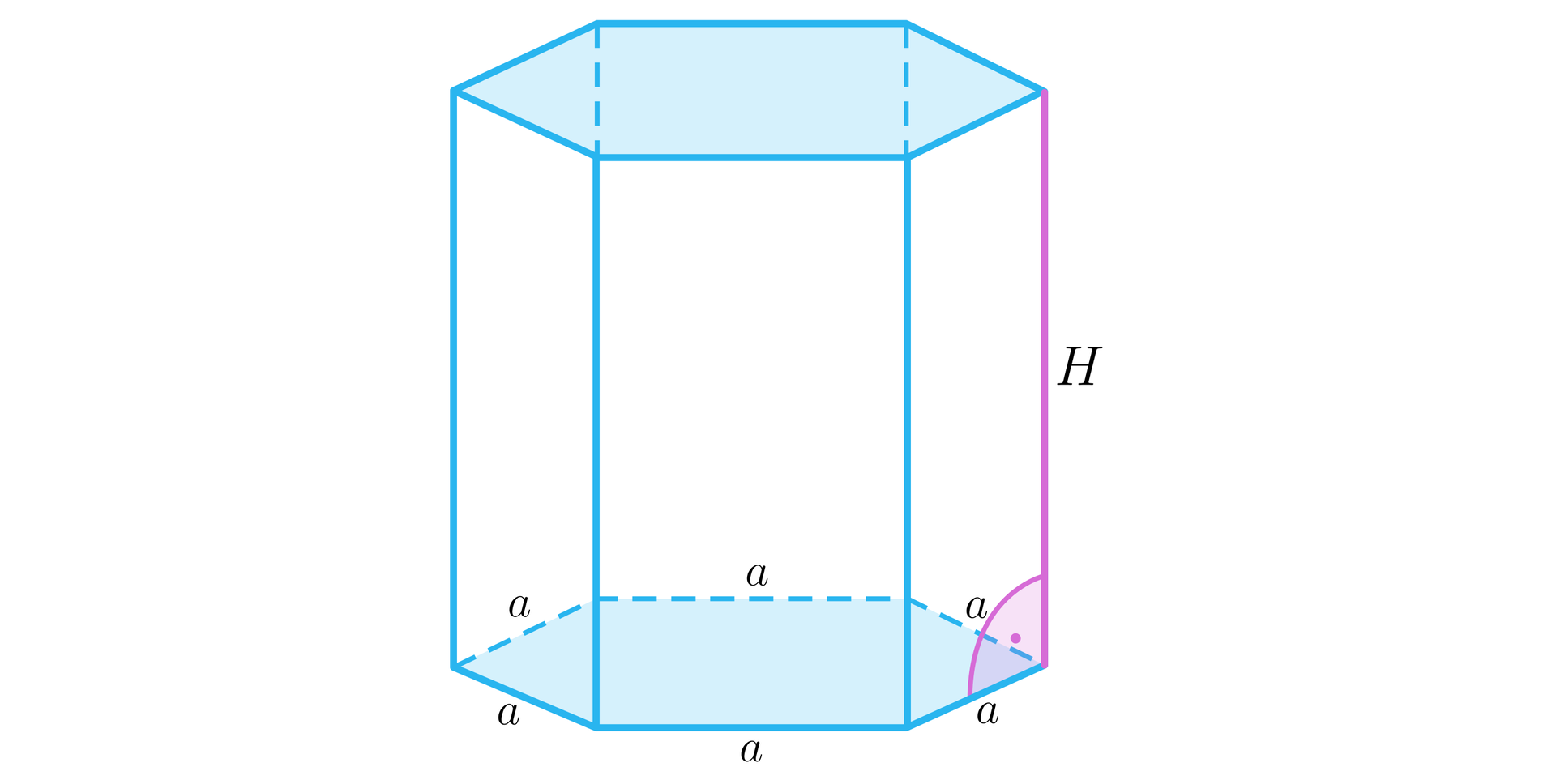
W graniastosłupie prawidłowym sześciokątnym suma długości krótszej przekątnej podstawy graniastosłupa i wysokości wynosi $10 cm$ . Wiedząc, że pole powierzchni całkowitej jest największe z możliwych, długość krawędzi podstawy wynosi:

$\frac{20 \sqrt{3}}{11} cm$
$\frac{40 \sqrt{3}}{23} cm$
$\frac{20 \sqrt{3}}{9} cm$
$\frac{10 \sqrt{3}}{3} cm$

Ćwiczenie 3

RiUz09toC582Q

R1BVh0u7reZfJ

Uzupełnij tekst, przeciągając odpowiedzi we właściwe miejsca. Przekątna graniastosłupa prawidłowego czworokątnego wynosi

10 cm

. Wiedząc, że pole powierzchni bocznej jest największe z możliwych, uzupełnij luki. Przyjmij,

a

- krawędź podstawy.
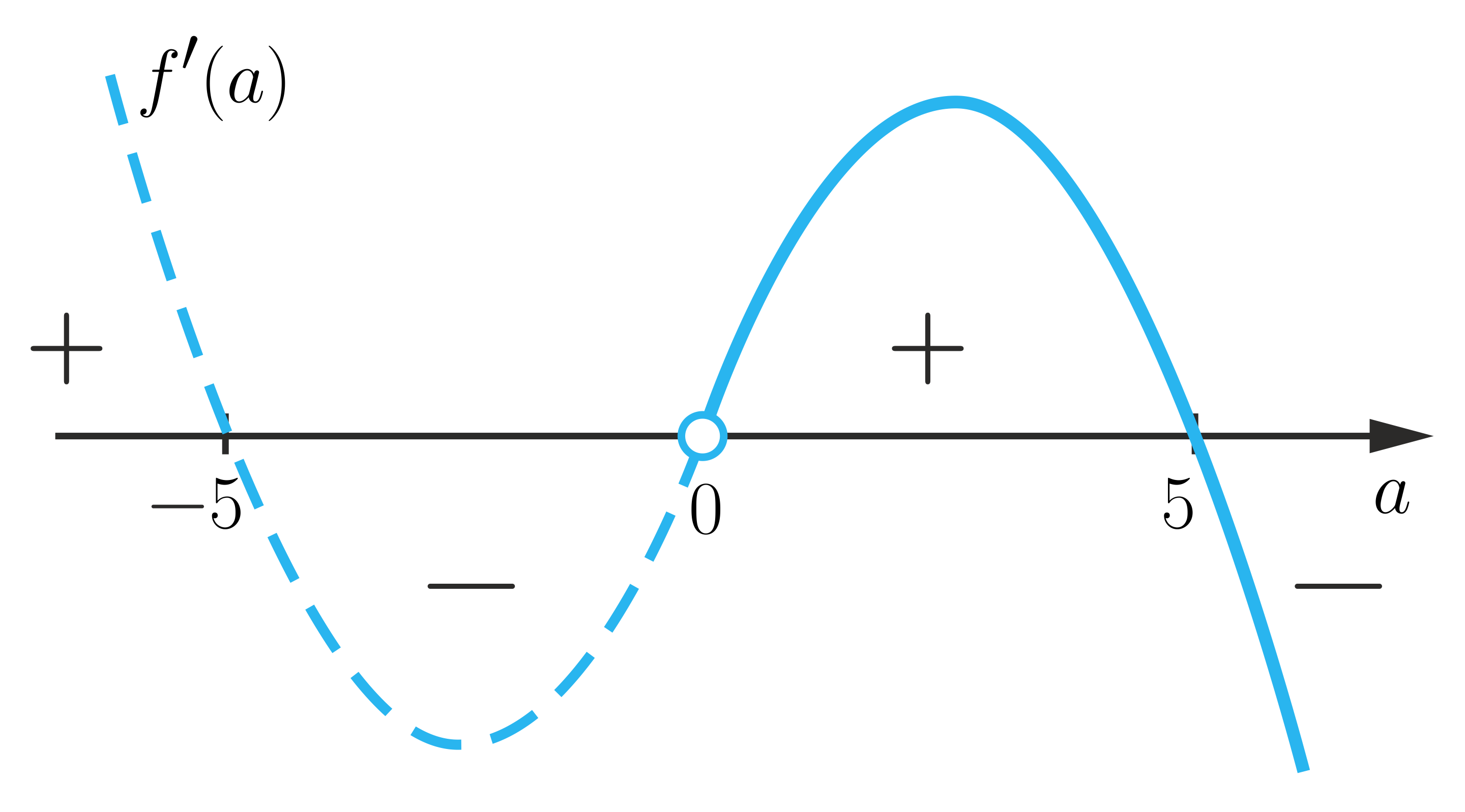
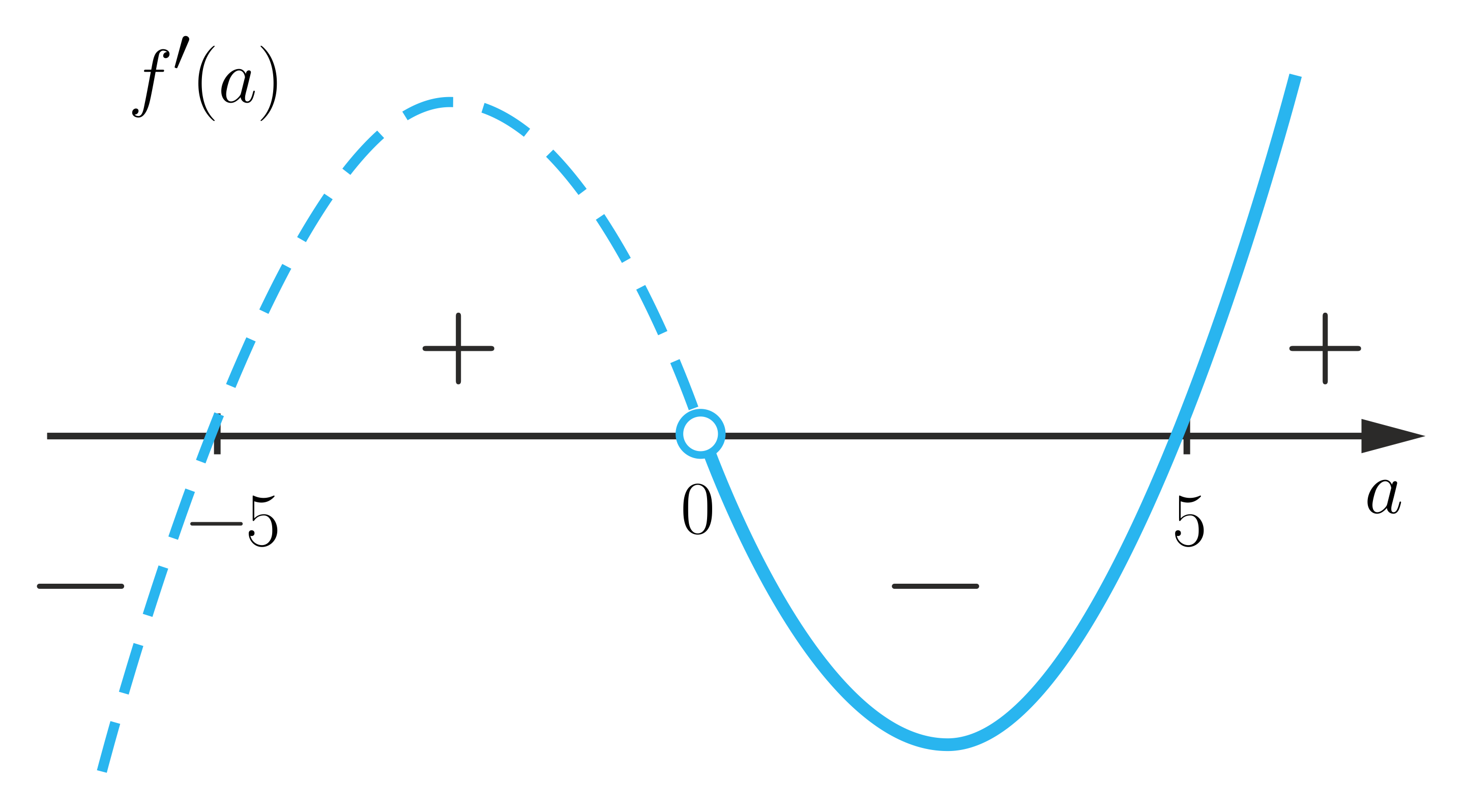
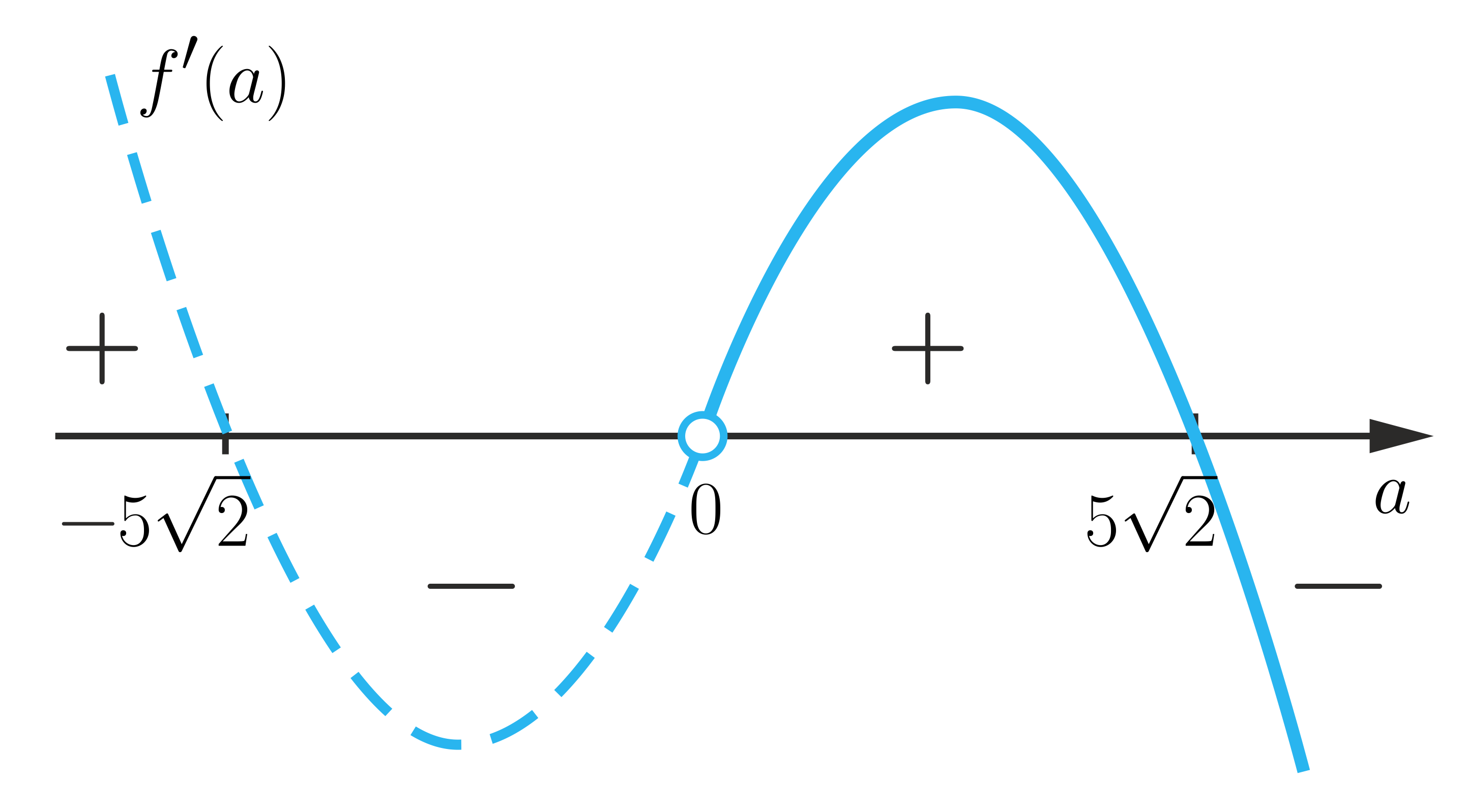
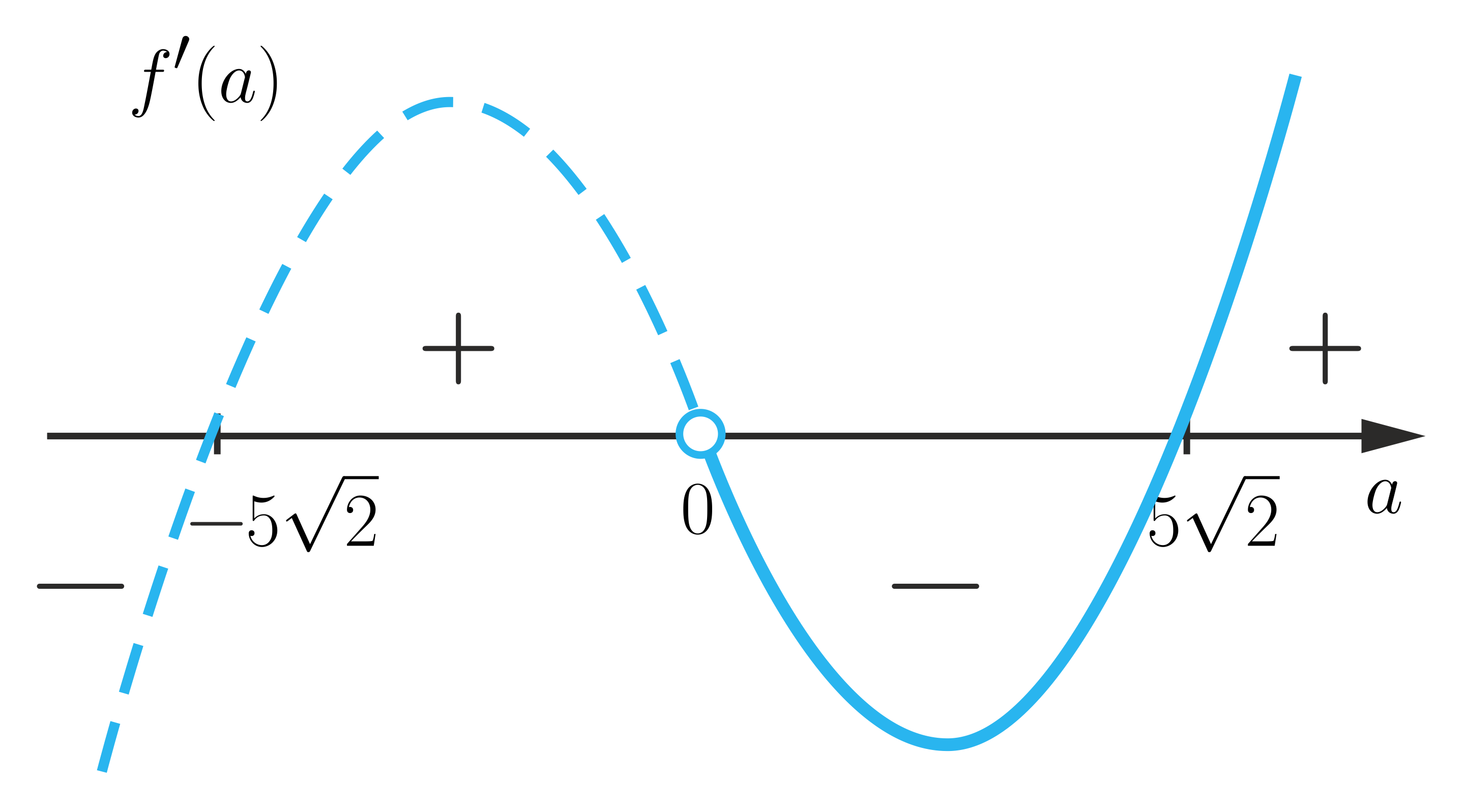
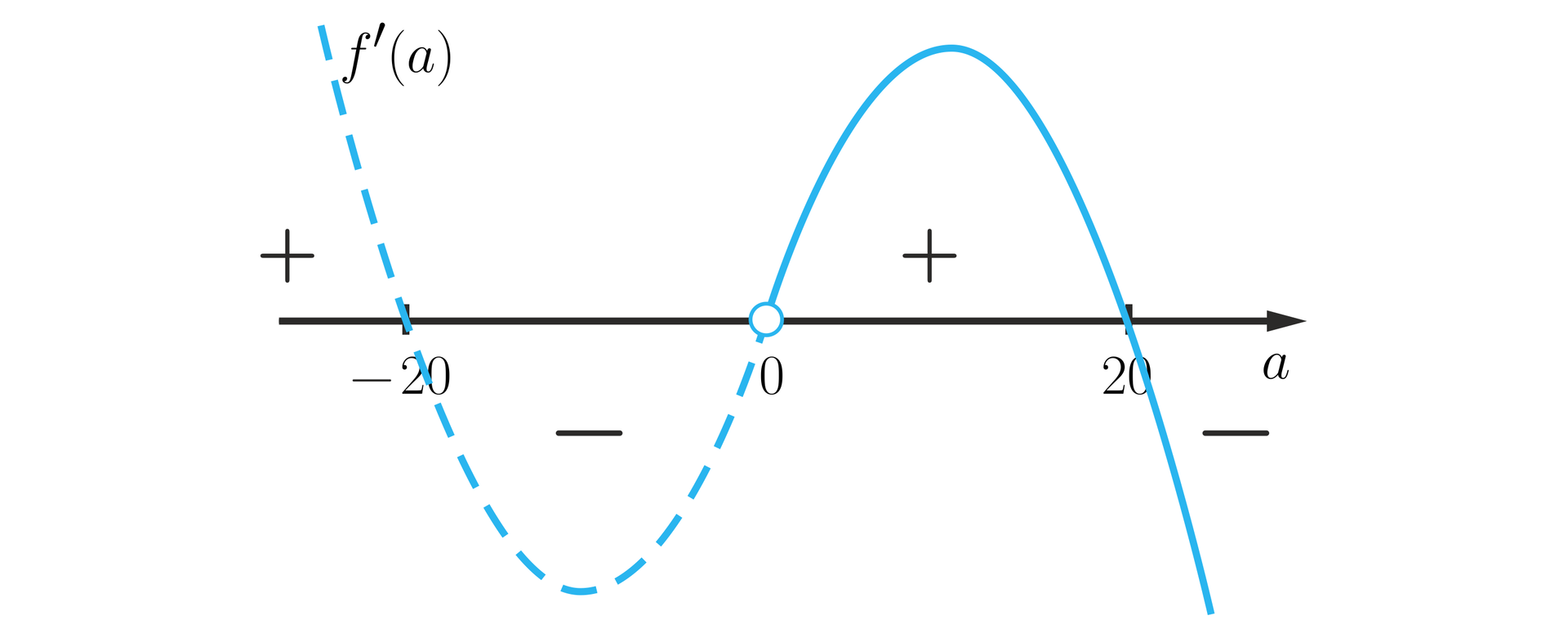
Dziedzina: 1.

5

, 2.

D = (5; + \infty)

, 3.

D = (0; + \infty)

, 4. rośnie, 5.

0

, 6.

- 5 \sqrt{2}

, 7. maleje, 8.

- 5

, 9.

5 \sqrt{2}

, 10. rośnie, 11. maleje.
Wykres pochodnej

f' (a)

umiejscowiony jest na osi

a

i przebiega następująco: najpierw 1.

5

, 2.

D = (5; + \infty)

, 3.

D = (0; + \infty)

, 4. rośnie, 5.

0

, 6.

- 5 \sqrt{2}

, 7. maleje, 8.

- 5

, 9.

5 \sqrt{2}

, 10. rośnie, 11. maleje do punktu 1.

5

, 2.

D = (5; + \infty)

, 3.

D = (0; + \infty)

, 4. rośnie, 5.

0

, 6.

- 5 \sqrt{2}

, 7. maleje, 8.

- 5

, 9.

5 \sqrt{2}

, 10. rośnie, 11. maleje, następnie 1.

5

, 2.

D = (5; + \infty)

, 3.

D = (0; + \infty)

, 4. rośnie, 5.

0

, 6.

- 5 \sqrt{2}

, 7. maleje, 8.

- 5

, 9.

5 \sqrt{2}

, 10. rośnie, 11. maleje do punktu 1.

5

, 2.

D = (5; + \infty)

, 3.

D = (0; + \infty)

, 4. rośnie, 5.

0

, 6.

- 5 \sqrt{2}

, 7. maleje, 8.

- 5

, 9.

5 \sqrt{2}

, 10. rośnie, 11. maleje, dalej 1.

5

, 2.

D = (5; + \infty)

, 3.

D = (0; + \infty)

, 4. rośnie, 5.

0

, 6.

- 5 \sqrt{2}

, 7. maleje, 8.

- 5

, 9.

5 \sqrt{2}

, 10. rośnie, 11. maleje do punktu 1.

5

, 2.

D = (5; + \infty)

, 3.

D = (0; + \infty)

, 4. rośnie, 5.

0

, 6.

- 5 \sqrt{2}

, 7. maleje, 8.

- 5

, 9.

5 \sqrt{2}

, 10. rośnie, 11. maleje i dalej 1.

5

, 2.

D = (5; + \infty)

, 3.

D = (0; + \infty)

, 4. rośnie, 5.

0

, 6.

- 5 \sqrt{2}

, 7. maleje, 8.

- 5

, 9.

5 \sqrt{2}

, 10. rośnie, 11. maleje.

RjfHJcp3j4sOe2

Ćwiczenie 4

Dokonano obrotu prostokąta, którego obwód wynosi $16 cm$ wokół osi symetrii przechodzącej przez krótszy bok. Wiedząc, że pole powierzchni bocznej otrzymanej figury jest największe z możliwych wskaż poprawną odpowiedź:

$P_{b} = 16 π {cm}^{2}$
$P_{b} = 32 π {cm}^{2}$
$P_{b} = 8 π {cm}^{2}$
$P_{b} = 16 {cm}^{2}$
$P_{b} = 32 {cm}^{2}$

Ćwiczenie 5

Dany jest graniastosłup prawidłowy sześciokątny o objętości $36$ . Wiedząc, że pole powierzchni całkowite jest najmniejsze z możliwych wyznacz to pole.

Wzór na objętość graniastosłupa wynosi $V = P_{p} \cdot H$ . W podstawie znajduje się sześciokąt, więc podstawę możemy podzielić na sześć trójkątów równobocznych. $P_{p} = 6 \cdot \frac{a^{2} \sqrt{3}}{4}$ .

RfLDLmsHsLyCO

Ilustracja przedstawia graniastosłup prosty sześciokątny o boku sześciokąta foremnego podstawy równym a oraz o wysokości H.

Wyznaczając wysokość ze wzoru na objętość oraz podstawiając wyznaczone pole podstawy otrzymujemy

$H = \frac{8 \sqrt{3}}{a^{2}}$ .

Pole powierzchni całkowitej wynosi

$P_{c} = 2 P_{p} + P_{b} = 3 a^{2} \sqrt{3} + 6 a H$ .

Podstawiając

$P_{c} (a) = 3 a^{2} \sqrt{3} + \frac{48 \sqrt{3}}{a}$ .

Wyznaczymy dziedzinę

$D$ : $a \in (0, \infty)$ .

Wyznaczymy pochodną

$P_{c}' (a) = 6 a \sqrt{3} - \frac{48 \sqrt{3}}{a^{2}}$ .

Miejscem zerowym pochodnej jest $a = 2$ . Naszkicujemy wykres pochodnej.

Rz4KHAZN48sWf

Ilustracja przedstawia poziomą oś a oraz wykres pochodnej P prim indeks dolny c będący ukośną prostą. Wykres maleje, osiąga minimum w punkcie 2, a następnie rośnie.

Z wykresu możemy zauważyć, że funkcja maleje a potem rośnie więc w $2$ osiąga minimum.

Wyznaczymy pole powierzchni całkowitej $P_{c} = 36 \sqrt{3}$ .

Pole powierzchni całkowitej wynosi $P_{c} = 36 \sqrt{3}$ .

R1Hj3XOCfCMil3

Ćwiczenie 6

Krawędź boczna ostrosłupa prawidłowego trójkątnego jest równa $10$ . Uzupełnij tabelę wiedząc, że pole powierzchni bocznej jest największe z możliwych. Przyjmij $a$ - krawędź podstawy oraz $P_{b} (a) = \sqrt{f (a)}$ .

MIN, BRAK, $↘$ , $↗$ , $+$ , $-$ , $(10 \sqrt{2}, \infty)$ , $(10 \sqrt{3}, \infty)$ , $10 \sqrt{3}$ , $(0, 10 \sqrt{3})$ , $(10 \sqrt{3}, 20)$ , $(4, \infty)$ , $4$ , $(0, 4)$ , $(4, \frac{20 \sqrt{3}}{3})$

$a$	$f' (a)$	$f (a)$

Ćwiczenie 7

W graniastosłupie prawidłowym czworokątnym punkty $O$ , $N$ i $M$ są, odpowiednio, środkami odcinków $A D$ , $D C$ i $E F$ .

R1CesbfaO27fG

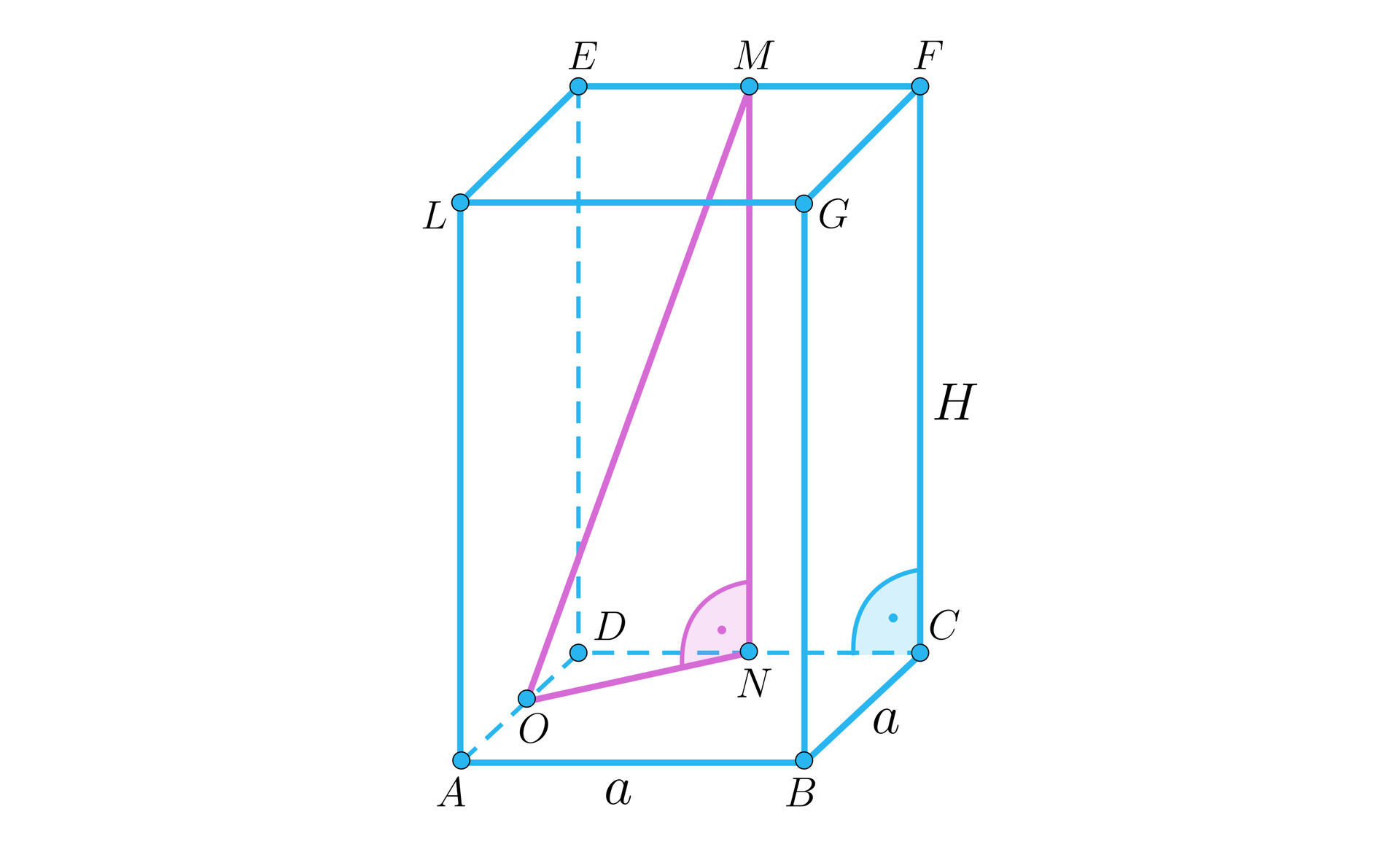
Ilustracja przedstawia prostopadłościan o kwadracie A B C D w podstawie dolnej i o kwadracie L G F E w podstawie górnej. Kwadrat ma bok o długości a. Wysokość bryły to H. Na krawędzi E F zaznaczono punkt M, a pod nim na krawędzi D C punkt N. Odcinek M N jest prostopadły do krawędzi podstawy D C. Na krawędzi A D zaznaczono punkt O i wykreślono między tymi trzema punktami trójkąt prostokątny O N M, gdzie On to pozioma przyprostokątna, M N pionowa przyprostokątna, a M O przeciwprostokątna.

Rozważmy trójkąt prostokątny $O M N$ . Przeciwprostokątna otrzymanego trójkąta wynosi $20 cm$ . Wiedząc, że pole powierzchni bocznej graniastosłupa jest największe z możliwych wyznacz to pole.

Oznaczmy

R1CesbfaO27fG

Przekątna $A C$ podstawy graniastosłupa wynosi $a \sqrt{2}$ . W związku z tym, że boki są połączone w połowie to ze skali podobieństwa odcinek $O N$ ma długość $\frac{a \sqrt{2}}{2}$ . Oczywiście $|M N| = H$ , więc z twierdzenia Pitagorasa mamy równość:

$20^{2} = H^{2} + {(\frac{a \sqrt{2}}{2})}^{2}$ .

Wyznaczając wysokość

$H = \sqrt{400 - \frac{a^{2}}{2}}$ .

Następnie wyznaczymy dziedzinę, boki muszą być dodatnie więc $a > 0$ oraz $400 - \frac{a^{2}}{2} > 0$ wyliczając otrzymujemy

$D : a \in (0, 20 \sqrt{2})$ .

Pole powierzchni bocznej wynosi

$P_{b} = 4 a H$ .

Podstawiając

$P_{b} (a) = 4 a \sqrt{400 - \frac{a^{2}}{2}}$ .

Kontynuując

$P_{b} (a) = 4 \sqrt{400 a^{2} - \frac{a^{4}}{2}}$ .

Interesuje nas dla jakiego argumentu $a$ funkcja $P_{b} (a)$ osiągnie największą wartość, wystarczy by wyrażenie pod pierwiastkiem się zmaksymalizowało. Rozważmy

$f (a) = 400 a^{2} - \frac{a^{4}}{2}$ .

Wyznaczymy pochodną

$f' (a) = 800 a - 2 a^{3}$ .

Miejscami zerowymi pochodnej są $a_{1} = - 20$ , $a_{2} = 0$ oraz $a_{3} = 20$ . Uwzględniając dziedzinę $a_{3} = 20$ . Naszkicujemy wykres pochodnej.

R11RnZx3ItmsP

Ilustracja przedstawia poziomą oś a z zaznaczonymi punktami: minus 20, 0 i 20, przy czym punkt 0 zaznaczono niezamalowanym kółkiem. Na rysunku zaznaczono sinusoidalny wykres pochodnej f prim. Wykres ma sinusoidalny kształt i biegnie linią przerywaną nad osią do punktu minus 20, gdzie przebija pod oś, dalej biegnie do zera, gdzie przebija nad oś. Od zera wykres biegnie linią ciągłą nad osią do punktu 20, gdzie przebija pod oś. Części wykresu nad osią oznaczono plusami, a pod osią minusami.

Z wykresu możemy zauważyć, że przed miejscem zerowym pochodnej funkcja rośnie a później maleje. W związku z czym przyjmuje największą wartość dla $a = 20$ . Wyznaczymy $H = \sqrt{400 - \frac{20^{2}}{2}} = \sqrt{200} = 10 \sqrt{2}$ . Podstawiając do pola powierzchni bocznej otrzymujemy $P_{b} = 4 \cdot 20 \cdot 10 \sqrt{2} = 800 \sqrt{2}$ .

Pole powierzchni bocznej wynosi $800 \sqrt{2}$ .

Ćwiczenie 8

W graniastosłup prawidłowy czworokątny o objętości $4 \sqrt{2}$ wpisano stożek o jak najmniejszym polu powierzchni bocznej.

RNtrNj1EWtGqi

a) uzupełnij tabelę przyjmując, że $a$ jest krawędzią podstawy graniastosłupa, oraz $P_{b} (a) = \sqrt{f (a)}$ .

MAX, BRAK, $↘$ , $↗$ , $+$ , $-$ , $(0, 1)$ , $1$ , $(1, \infty)$ , $(4, \infty)$ , $4$ , $(0, 4)$

$a$	$f' (a)$	$f (a)$

RdxiMNGtlEty3

b) Wyznacz pole powierzchni bocznej

$3 π$ , $\sqrt{3} π$ , $5 π$ , $\sqrt{5} π$

$P_{b} =$ ............

Animacja 3D

Dla nauczyciela