Sprawdź się
Pokaż ćwiczenia:
Ćwiczenie 1
W wyniku przekształcenia wykresu funkcji w symetrii częściowej względem osi , a następnie otrzymanego wykresu w translacji o wektor , otrzymamy wykres funkcji o wzorze: Możliwe odpowiedzi: 1. , 2. , 3. , 4.
W wyniku przekształcenia wykresu funkcji w symetrii częściowej względem osi , a następnie otrzymanego wykresu w translacji o wektor , otrzymamy wykres funkcji o wzorze:
Ćwiczenie 2
Jakie przekształcenia trzeba wykonać, aby z wykresu funkcji otrzymać wykres funkcji ?
- Symetria względem osi , translacja o wektor .
- Symetria względem osi , translacja o wektor .
- Symetria względem osi , translacja o wektor .
- Translacja o wektor , symetria względem osi .
Ćwiczenie 3
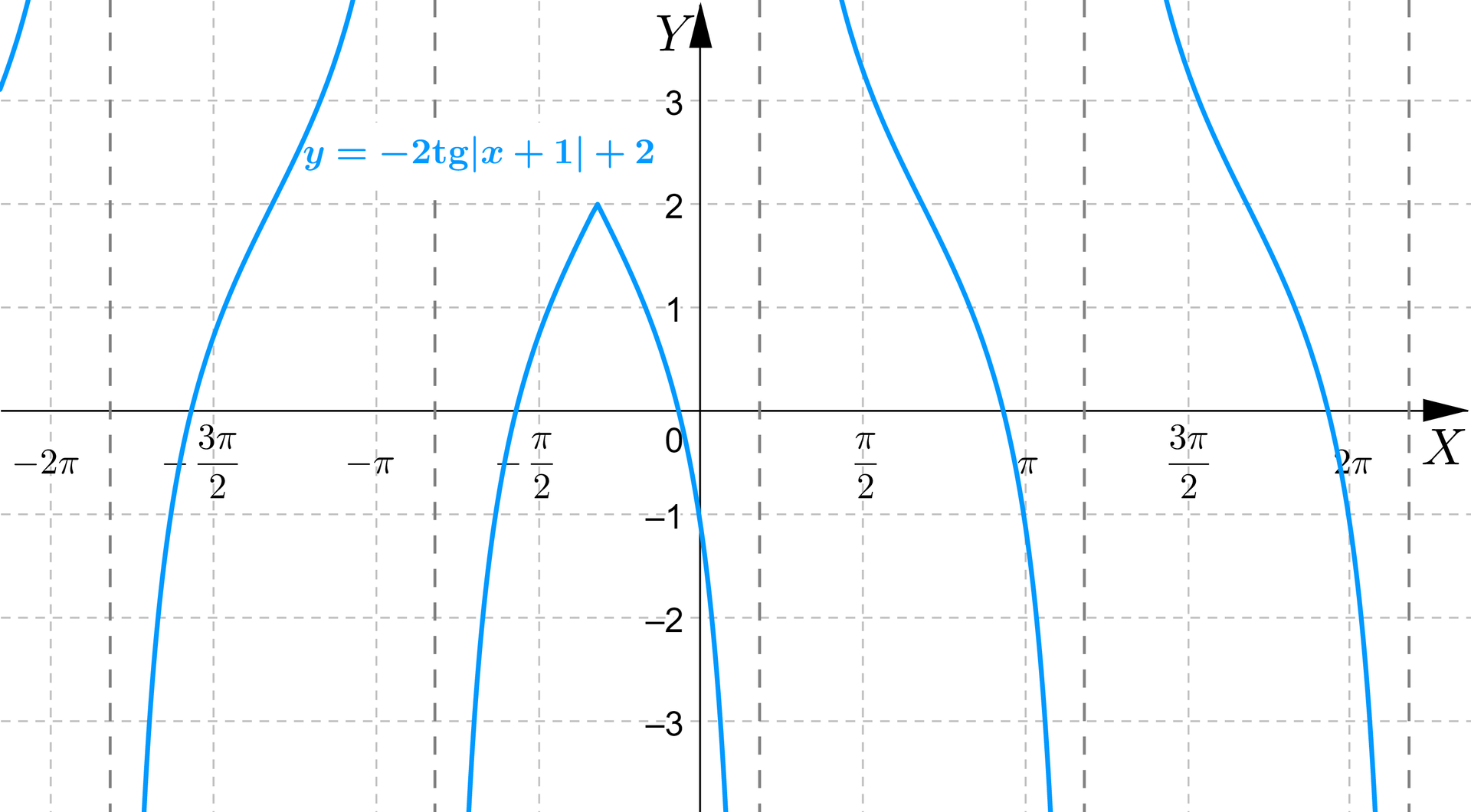
Zaznacz prawidłową odpowiedź. Możliwe odpowiedzi: 1. Miejsca zerowe narysowanej funkcji to: 0, , ,, 2. Miejsca zerowe narysowanej funkcji to: 0, , ,., 3. Miejsca zerowe narysowanej funkcji to: , , 4. Miejsca zerowe narysowanej funkcji to: ,
Ćwiczenie 4
Ułóż w kolejności przekształcenia, za pomocą których z wykresu otrzymamy wykres funkcji .
- translacja o wektor
- translacja o wektor
- powinowactwo o osi i skali
- symetria częściowa względem osi
Ćwiczenie 5
Ułóż w kolejności przekształcenia, za pomocą których z wykresu otrzymamy wykres funkcji .
- powinowactwo o osi i skali
- symetria względem osi
- translacja o wektor
- symetria częściowa względem osi
Ćwiczenie 6
Ćwiczenie 7
Opisz przekształcenia, jakie należy wykonać, aby z wykresu funkcji otrzymać wykres funkcji .
Ćwiczenie 8
Narysuj wykres funkcji .
Ćwiczenie 8
Jak otrzymać wykres funkcji ? Opisz kolejne kroki.